Ultrabright γ-ray emission from the interaction of an intense laser pulse with a near-critical-density plasma*

Aynisa Tursun(阿依妮萨图尔荪) Mamat Ali Bake(买买提艾力巴克) Baisong Xie(谢柏松)Yasheng Niyazi(亚生尼亚孜) and Abuduresuli Abudurexiti(阿不都热苏力阿不都热西提)

1School of Physics Science and Technology,Xinjiang University,Urumqi 830046,China

2Key Laboratory of Beam Technology of the Ministry of Education,and College of Nuclear Science and Technology,Beijing Normal University,Beijing 100875,China

3Institute of Physics and Electrical Engineering,Kashi University,Kashgar 844009,China

Keywords: electron acceleration, γ-ray emission, inverse Compton scattering, near-critical-density plasma,2D-QED-PIC simulation

1. Introduction

Owing to the rapid development of laser technology,[1,2]ultra-intense (1022W/cm2) and ultrashort (a few femtoseconds) laser pulses can be obtained in the laboratory.[3]Laser intensities in the order of 1023-1025W/cm2are expected to become available in the next few years.[4,5]When an ultrahighintensity laser interacts with a plasma,the electron motion becomes relativistic,[6,7]and quantum electrodynamics (QED)effects such asγ-ray emission[8]and electron-positron pair production become significant.[9,10]Considerable theoretical and numerical[11-13]research on the generation of high-energy electrons and ultrabrightγ-rays has been conducted for applications in medicine,[14]industry,[15]and astrophysics.[16]Many researchers have proposed various schemes for obtaining high-energy electron sources forγ-ray generation, such as laser-driven direct laser acceleration (DLA),[17,18]radiation pressure acceleration,[19]and laser wakefield acceleration(LWFA).[20,21]Among them, LWFA is the most widely studied and thought to be a more straightforwardγ-ray emission mechanism,along with the all-optical mechanism.[22]

Recent studies have shown that electron beams with energies as high as several GeV can be obtained from laser-plasma interactions using LWFA,[23,24]andγ-photons with energies beyond the GeV regime can be produced by nonlinear Compton scattering as the wakefield-accelerated electron beam interacts with the reflected laser pulse.[25,26]Many researchers have studied effective mechanisms for producingγ-rays with a peak brilliance of 1020-1026photons/s/mm2/mrad2/0.1%BW at MeV to GeV energies using lasers with intensities of 1021-1023W/cm2.[27,28]Zhuet al.[29]recently obtainedγ-rays with a peak brilliance of 1026photons/s/mm2/mrad2/0.1%BW at 1 MeV using a multi-petawatt laser pulse in a two-stage wakefield accelerator. Guet al.[30]proposed a new mechanism for generating brilliantγ-rays using a plasma mirror and obtainedγ-rays with a peak intensity of 0.74 PW and a brilliance of 1024photons/s/mm2/mrad2/0.1%BW at 58 MeV under a laser intensity of 1023W/cm2. In a recent study, we investigated an efficient method of generating high-energyγ-photons using the interaction between a wakefield-accelerated electron beam and a counter-propagating high-intensity laser pulse with a compound target, and obtained two groups ofγ-rays with a small divergence angle.[31]Changet al.[32]proposed a new resonance acceleration scheme for generating relativistic electron bunches and brilliantγ-rays, used a three-dimensional particle-in-cell (PIC) simulation and reportedγ-ray pulses with a peak brilliance of 1025photons/s/mm2/mrad2/0.1%BW(15 MeV) at a laser intensity of 1.9× 1023W/cm2.More recently, Zhanget al.[33]reported nano-micro array thin target for ultra-short (440 as) and ultra-bright[1024photons/s/mm2/mrad2/0.1%BW(15 MeV)]γ-ray emission with high conversion efficiency. These high-energy electrons andγ-rays represent a novel light source with a broad range of applications in the production of high-energy electron-positron pairs,exploring high-energy astrophysics in the laboratory,and performing nuclear physics research.[34,35]

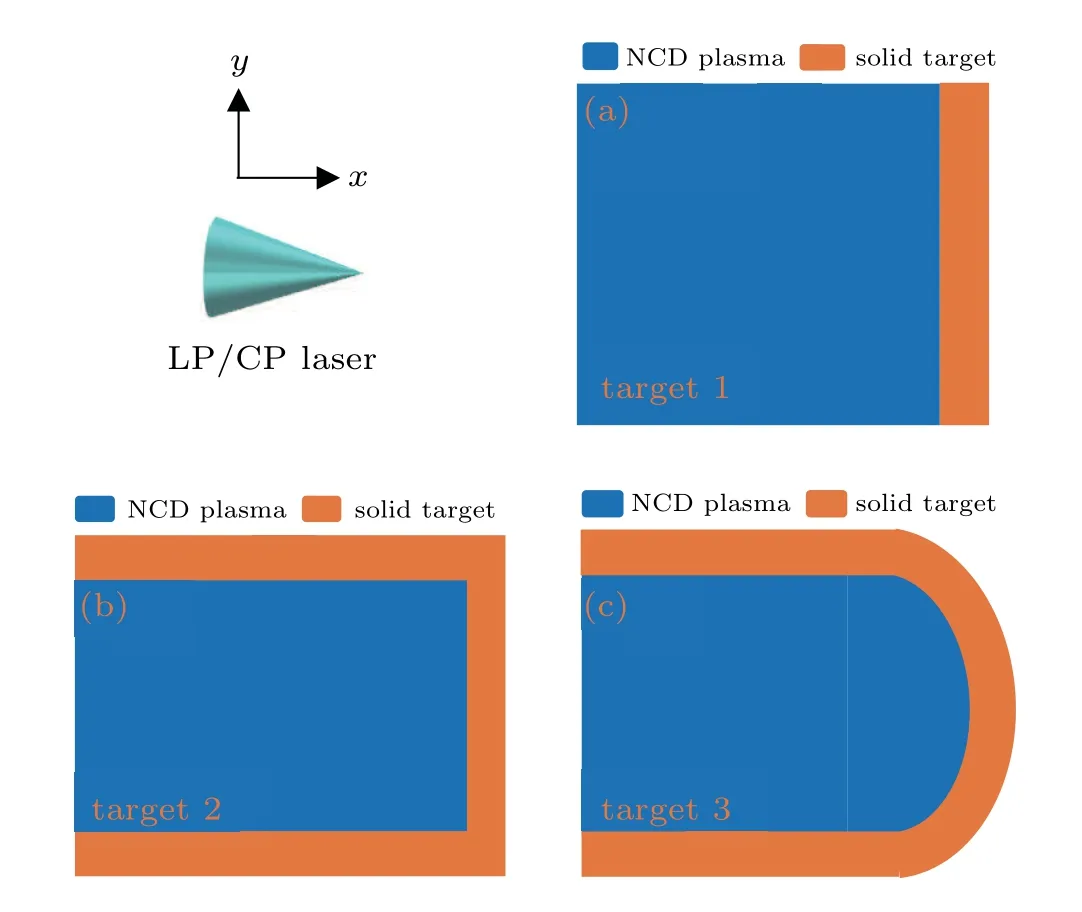
Fig.1. Schematic diagram of ultrabright γ-ray emission from the interaction of an intense LP laser and a compound target. The targets consist of a uniform NCD hydrogen plasma with a density of ne=nc and an aluminum solid foil with a density of ne=700nc.Blue and orange represent the NCD plasma and solid target,respectively.

In this study, we investigate the generation of highenergy, ultrabrightγ-rays by the interaction of an intense linearly polarized (LP) laser with a near-critical-density (NCD)plasma using two-dimensional(2D)QED PIC simulations. In the simulations,three target configurations are used to investigate the effects of target shape onγ-ray generation,as shown in Fig. 1. Theγ-photon density, energy, angular distribution,and peak brightness for each target are compared in detail.The results show that when a laser pulse with an intensity of 8.5×1022W/cm2propagates in an NCD plasma, a large amount of electrons are trapped by the self-generated magnetic field and radiation reaction(RR)trapping effects and accelerated to high energy. Consequently,γ-rays are emitted by nonlinear betatron oscillation in the first stage and by nonlinear Compton scattering in the second stage. The accelerated electrons emit GeVγ-photons by inverse Compton scattering when they collide with the reflected laser pulse. The simulation results indicate that target 3 affords better focusing of both the laser field and electron beam compared to targets 1 and 2.Consequently, well-collimatedγ-rays with high energy, high density, and low divergence angle are produced when target 3 is used. The density and cutoff energy of both the accelerated electrons and the emittedγ-rays are much higher than those obtained by other proposed mechanisms[36,37]using the same driving laser. The angular distribution of theγ-rays is within approximatelyθ ≤20°, and the cutoff energies of the accelerated electrons andγ-photons exceed 3 GeV and 2 GeV,respectively. The brilliance of theγ-rays and the conversion efficiency are higher than those reported in Ref. [38], where two counter-propagating intense laser pulses were used. The results demonstrate that it is essential to optimize the shape of the solid target to enhance theγ-ray energy and brilliance and the conversion efficiency.

2. Theoretical model of γ-ray emission

When an ultrahigh-intensity laser pulse interacts with a plasma,electrons are simultaneously affected by the RR force and emit high-energyγ-photons. When the laser intensity is relatively high, the RR force becomes non-negligible.[39]In laser-plasma interactions, the relativistic gauge-invariant parameterχedetermines the importance of the nonlinear QED effects and the ratio ofγ-ray emission.[40]In the classical description,the total radiation power of the accelerated electrons is written as[41]

whereF= dP/dt,Pis the electron momentum,meandeare the mass and charge of the electron, respectively,cis the speed of light in vacuum, andγeis the electron Lorentz factor. The classical description of electron radiation in a strong electromagnetic field overestimates the total emitted power.In the quantum description, the emitted photon energy may not exceed the electron energy, whereas there is no such restriction in the classical description. We introduce the quantum effect functionG(χe), which decreases the electron radiation power,[43]into the classical expression. The quantum effects can be expressed as[42]

3. Simulation setups

To test our model, a 2D-PIC simulation was conducted using the EPOCH code,[44]which takes into account of the QED effects via a Monte Carlo algorithm. In our simulation,the simulation box has dimensions of(110×24)µm in thexandydirections, respectively, and is divided into 3300×400 grid cells,with 10 macroparticles in each cell.An LP Gaussian laser pulse with an intensity ofI0=8.5×1022W/cm2enters the simulation box from the left boundary att=0. The corresponding normalized amplitude isa0=eE0/mecω0=250,

whereE0andω0are the laser electric field strength and laser frequency,respectively. The laser pulse duration isτ=15 fs,the laser wavelength isλ0=1 µm, and the spot size of the laser isr0=5µm in all the simulations. Three target configurations are considered,as shown in Fig.1. For target 1,a flat foil with no channel is attached behind the NCD plasma, as shown in Fig.1(a). Flat and curved foils with an NCD plasma channel are used as targets 2 and 3,as shown in Figs.1(b)and 1(c), respectively. The NCD plasma is a uniform hydrogen plasma with a densityne=nc,and solid aluminum foils with a densityne=700ncare used,whereneis the electron density,andnc=meω20/4πe2is the critical density. The NCD plasma is located betweenx=10µm andx=100µm, and betweeny=−6µm andy=6µm,and the thickness of the aluminum foil is 2µm.Simple outflow and periodic boundary conditions are applied in thexandydirections,respectively.

4. Simulation results

Figure 3 shows the density distributions of electrons and photons for each target after laser reflection(t=360 fs). Under the same laser and NCD plasma conditions, the electron and photon density profiles for targets 2 and 3 are completely different from that for target 1. For target 1, because of inefficient focusing by the self-generated magnetic field, a large number of electrons escape the channel center, and thus the electron beam has a large source size, as shown in Fig. 3(a).Consequently,γ-rays with low density and a large source size are produced, as shown in Fig. 3(b). However, for targets 2 and 3,because the self-generated magnetic field affords better focusing, electrons are confined in a small space on the laser propagation axis and produce high-densityγ-rays with a density distribution similar to that of the electrons, as shown in Figs. 3(d) and 3(f). The photon density was approximately 90ncand 120ncfor targets 2 and 3, which are three and four times higher, respectively, than the value of approximately 30ncfor target 1. The results indicate that up and down solid foils(the channel)plays an important role in focusing the laser and generating a magnetic field,which is favorable for obtaining a low-divergence, high-density electron beam andγ-rays.Note that more tightly focused and denserγ-photons are generated when target 3 is used than when target 2 is used. The reason is that target 3 provides better focusing of the laser field as well as the electrons.

Figure 4 shows the energy spectra of electrons andγphotons for each target configuration att=300 and 360 fs(before and after laser reflection, respectively). In the first stage of the interaction,an intense laser propagates in the NCD plasma. Because of the additional contributions of the selfgenerated magnetic field and RR trapping effect,a large number of electrons are trapped and accelerated to high energy.The cutoff energy of the accelerated electrons att=300 fs is 3 GeV for target 3 but only approximately 1.5 GeV for target 1, as shown in Fig.4(a). Consequently, some low-energyγ-photons are emitted via nonlinear betatron oscillation when target 1 is used,as shown in Fig.4(b). However,theγ-photon cutoff energies for targets 2 and 3 are much higher than that for target 1. This result also indicates that the NCD plasma channel plays a key role in the generation of high-energyγ-rays.In the second stage,the accelerated electrons collide with the counter-propagating reflected laser, and the strong ponderomotive force of the laser changes the electron direction and thus increases the electron Lorentz factorγe. Therefore, the value of the quantum invariant parameterχeis maximized,increasing the probability ofγ-ray emission and theγ-ray energy. In this stage,because nonlinear Compton scattering occurs, the energy of some of the accelerated electrons is decreased, and high-energyγ-photons are emitted, as shown in Fig.4(d).Note that,for target 3,the cutoff energy ofγ-photons is 2.2 GeV,whereas it is only approximately 500 MeV for target 1.

Fig.2. Distribution of self-generated magnetic field Bz in(x,y)plane for three targets before(t =350 fs,top row)and after(t =360 fs,bottom row)laser reflection. The magnetic field is normalized by B0=meω0/e.

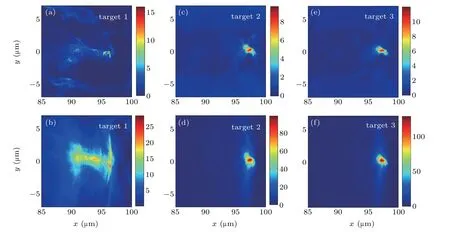
Fig.3. Distribution of electron(top row)and photon(bottom row)densities in(x,y)plane for each target after laser reflection(t=360 fs). The electron and photon densities are normalized by the critical density nc.

Fig.4. Energy spectra of electrons[(a)and(c)]and γ-photons[(b)and(d)]for each target before(top row)and after(bottom row)laser reflection.

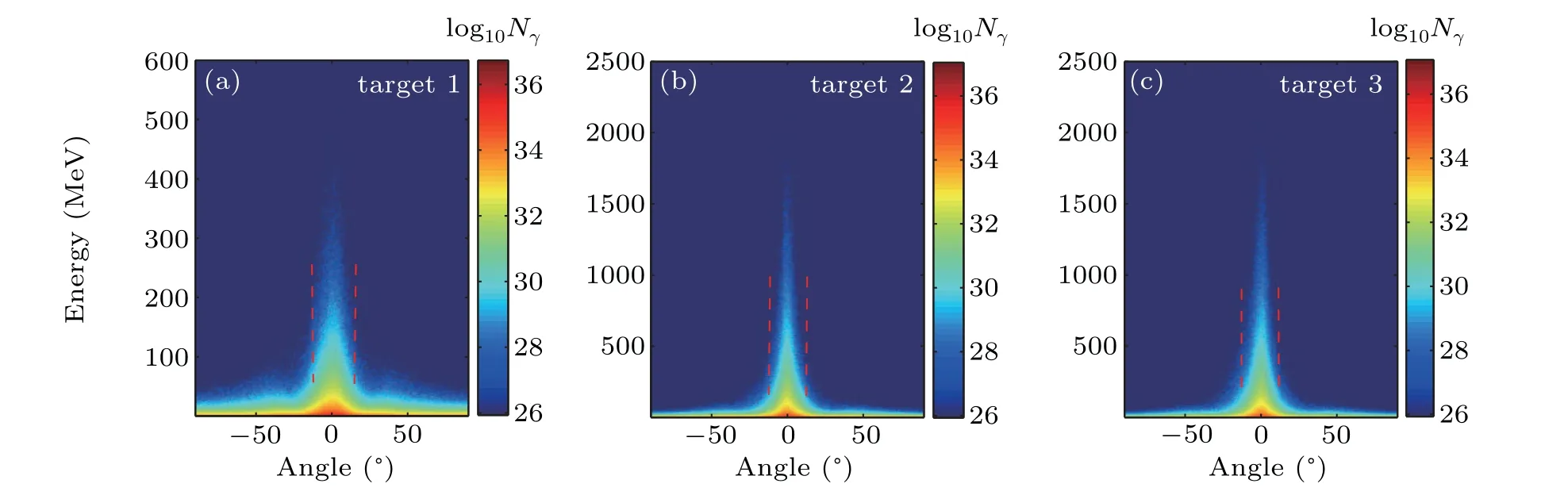
Fig. 5. Energy angular distribution of γ-photons for each target after laser reflection (t =360 fs). The color bar shows the photon number (Nγ) on a logarithmic(log10 Nγ)scale with arbitrary units.

Table 1. γ-ray peak brilliance B(k)(photons/s/mm2/mrad2/0.1%BW)for each target at t=360 fs.

Figure 5 plots the energy angular distribution ofγphotons for each target configuration after laser reflection(t= 360 fs). Low-energyγ-photons with a large divergence angle (～37°) are generated when target 1 is used,as shown in Fig. 5(a). However, for targets 2 and 3,the divergence angles of theγ-photons are approximately 25.5°and 20.5°, as shown in Figs. 5(b) and 5(c), respectively. The correspondingγ-ray peak brilliance for each target att= 360 fs is given in Table 1. It can be concluded that, for target 1, there are 2×1014and 3.67×1011photons at 100 MeV and 500 MeV, respectively, within a source size of 7.2×4 µm2, which gives a peak brightness of approximately 1×1024photons/s/mm2/mrad2/0.1%BW at 100 MeV and 2×1021photons/s/mm2/mrad2/0.1%BW at 500 MeV. By contrast, for target 2, the peak brightness of theγ-rays at 100 MeV (source size is 1.63×2.05 µm2) is 1.6×1026photons/s/mm2/mrad2/0.1%BW, and for target 3,it is 4.6×1026photons/s/mm2/mrad2/0.1%BW(source size is 1.37×1.45 µm2), which is two orders of magnitude larger than that for target 1. The well-collimated, high-density, and ultrabrightγ-rays obtained using our scheme may be suitable for the generation of energetic positrons and for laboratory astrophysics research.

5. Discussion

The fraction of energy coupled to electrons and the relaxation time are related to the laser and plasma parameters, as discussed in previous papers.[45-47]Therefore,in this section,we discuss in detail the effects of plasma channel length, target curvature radius,laser polarization,laser intensity,and the RR force on the electron acceleration andγ-ray emission.

5.1. Effect of plasma channel length

We study the effects of NCD plasma channel length on the electron acceleration andγ-ray emission for target 3 with a fixed target curvature radius ofr=6µm. To ensure that the laser is reflected from the foil and collides with the accelerated electrons, we consider the following times and channel lengths:t=300 fs forL=80µm,t=330 fs forL=90µm,t=360 fs forL=100 µm,t=390 fs forL=110 µm, andt=420 fs forL=120µm. The simulation results show that for short channels, for example,L=80 µm andL=90 µm,trapped electrons are accelerated to lower energies because of the short acceleration distance, and thus lower-energy electrons andγ-photons are produced,as shown in Figs.6(a)and 6(b). However, for long channels, for example,L=110 µm andL=120µm,the travel time is longer,and most of the laser energy is depleted before laser reflection(the laser energy after reflection is approximately 100 J, which is one-tenth the initial laser energy). Under these conditions,the photons also have lower energies than those produced atL=100 µm. As shown in Fig. 9(b), the electron energy conversion efficiency increased linearly untilt=300 fs,remained constant for 60 fs,and then decreased. This result indicates that a long channel(i.e.,a long travel time)is not favorable for electron acceleration. When a channel length ofL=100µm is used,the accelerated electron cutoff energy is as high as 3 GeV,and the correspondingγ-photon energy exceeds that obtained using the other channel lengths. Figures 6(c) and 6(d) show that the peak brightness ofγ-photons and the conversion efficiency of laser energy to electrons andγ-photons are higher than those at the other channel lengths. This result shows that to obtain high-energyγ-rays,it is very important to choose an appropriate channel length.

Fig.6.Energy spectra of(a)electrons and(b)γ-photons,(c)γ-ray peak brilliance(photons/s/mm2/mrad2/0.1%BW),and(d)energy conversion efficiency of electrons and γ-photons for different plasma channel lengths.

Fig.7.Energy spectra of(a)electrons and(b)γ-photons,(c)γ-ray peak brilliance(photons/s/mm2/mrad2/0.1%BW),and(d)energy conversion efficiency of electrons and γ-photons for different target curvature radii after laser reflection(t=360 fs).

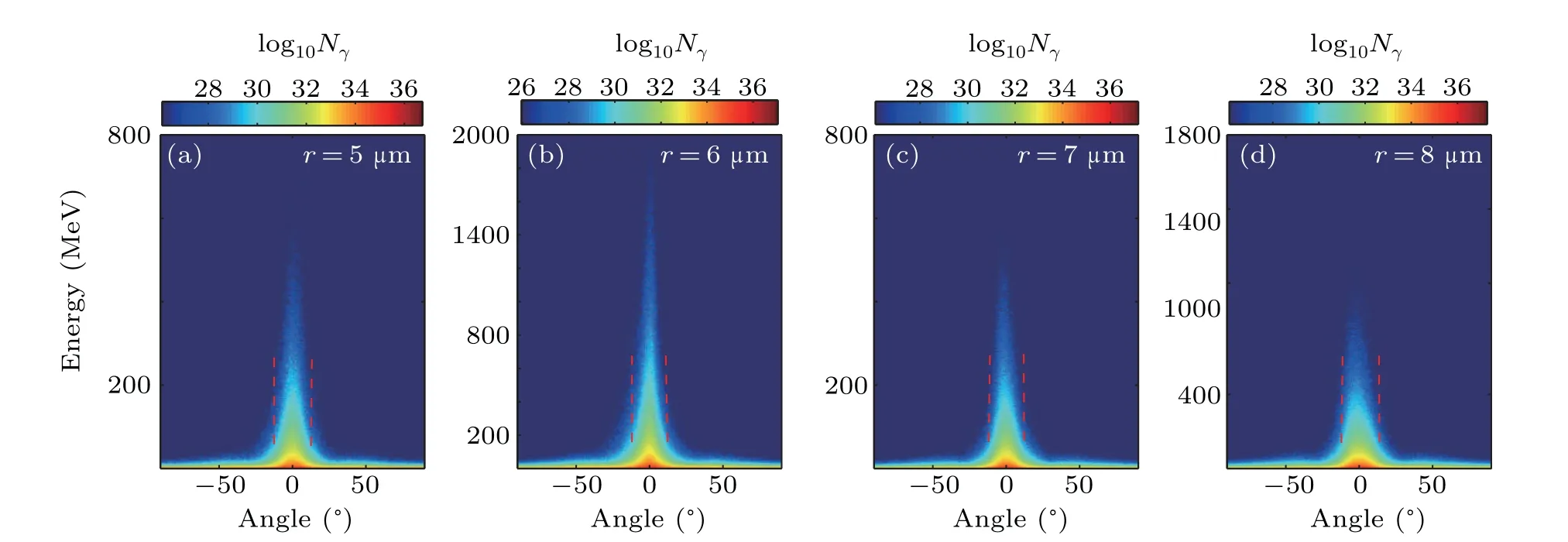
Fig. 8. Energy angular distribution of γ-photons for different foil curvature radii after laser reflection (t =360 fs). The color bar shows the photon number(Nγ)on a logarithmic(log10 Nγ)scale with arbitrary units.

5.2. Effect of target curvature radius

The effects of target curvature radius on the electron acceleration andγ-ray emission are also investigated for target 3 with a fixed channel length ofL=100µm. The simulation results show that when the radius of curvature of the target is equal to or smaller than the laser spot size,r0=5 µm, the number of trapped electrons is limited;thus,a relatively small number of electrons interact with the reflected laser,and thus the electron and photon energies are low,as shown in Figs.7(a)and 7(b). Figures 7(c)and 7(d)show that the peak brightness of theγ-rays and the energy conversion efficiency decrease with increasing curvature radius. The primary reason is that the laser field is less focused at a relatively large curvature radius, which results in a largeγ-ray divergence. In addition,the divergence angle ofγ-photons is also relatively wide at a small curvature radius, as shown in Fig. 8(a). Atr=6 µm,more electrons are trapped in the channel and they are accelerated to higher energy than in the other cases. Consequently,γ-photons with higher energy and a smaller divergence angle are emitted. For this optimal radius, the electron and photon cutoff energies are 3 GeV and 2.2 GeV, respectively, and the divergence angle of theγ-rays is approximately 20.5°, as shown in Fig.8(b). The results show that the maximum electron and photon energies both decrease significantly with increasing radius of curvature. From these simulation results,we can conclude that large and small curvature radii decrease the focusing of the laser field and the trapping of electrons in the channel,and ultimately decrease the maximum energy and increase theγ-ray divergences angle.For both simulations and experiments,it is crucial to select a target with an appropriate curvature radius to generate high-qualityγ-rays.

Fig.9. Energy spectra of(a)electrons and γ-photons for LP and CP lasers at t=360 fs,(b)time evolution of energy conversion efficiency for LP and CP lasers at t=360 fs.

5.3. Effect of laser polarization

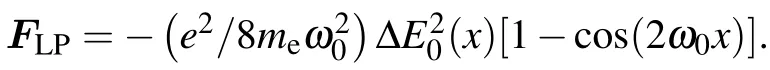
5.4. Effect of laser intensity

It is essential to investigate the effect of laser intensity on ultrabrightγ-ray emission from laser-plasma interaction.Using another simulation, we investigated the effect of laser intensity using the optimal laser (the LP laser) and plasma parameters and the results are summarized in the Table 2.The simulation results show that the electron andγ-ray energies increase with increasing laser intensitya0,as shown in Figs.10(a)and 10(b).The reason is that the higher laser intensity produces more energetic electrons owing to the combined effects of the stronger acceleration field, self-generated magnetic field, and RR trapping effect, ultimately strengthening the emission of well-collimatedγ-rays,as shown in Fig.10(c).Figure 10(d)shows the energy conversion efficiencies of electrons andγ-photons as a function of laser amplitudea0for the optimal laser and plasma parameters. The energy conversion efficiency of electrons increased linearly up toa0=150 and then increased more steeply witha0.The conversion efficiency to photons increased rapidly from a few percent to 26%, and the conversion efficiencies of electrons andγ-photons were comparable at approximatelya0=300 (see Table 2). As the laser intensity increased, photons absorbed more energy than electrons,as shown in Fig.10(d).

5.5. Effect of radiation reaction

For comparison, we also performed additional simulations without the RR effect using the optimal target parameters for the LP laser and the results are also summarized in the Table 2. The simulation results indicated that without the RR trapping effect,the strong ponderomotive force of the intense laser tends to push electrons from the high-intensity region.Consequently,few electrons are trapped in the channel center,and they diverge in the transverse direction at the acceleration stage, as shown in Figs.11(a)and 11(b). However, when the RR effect is considered,the electrons in the NCD plasma experience a strong RR force due to radiating photons. When the RR force becomes large enough to compensate for the expelling ponderomotive force of the laser, the RR causes electrons to be trapped inside the laser instead of removed by ponderomotive pressure.[48]Consequently,electrons gradually accumulate in the high-intensity region (channel center) and form a high-density electron bunch, as shown in Figs.11(a1)and 11(b1). This electron bunch then co-propagates with the laser pulse and is accelerated to high energy in the first stage;thus,it emits more high-energy,well-collimatedγ-photons in the first stage, as shown in Figs. 11(c1) and 11(d1). We see from this figure that the photon density exceeds 50ncwhen the RR is considered,which is much higher than that without the RR, as shown in Figs. 11(c) and 11(d). In the second stage of the interaction,this well-collimated electron beam counterpropagates with the reflected laser pulse, and theγ-ray emission is enhanced by inverse Compton scattering,as discussed in Section 4.

Fig.10. Energy spectra of(a)electrons and(b)γ-photons at t =360 fs. (c)Angular distribution of γ-photons at laser intensities of a0=50,100,150,200,250,and 300 at t=360 fs. (d)Energy conversion efficiencies of electrons and γ-photons at t=360 fs.

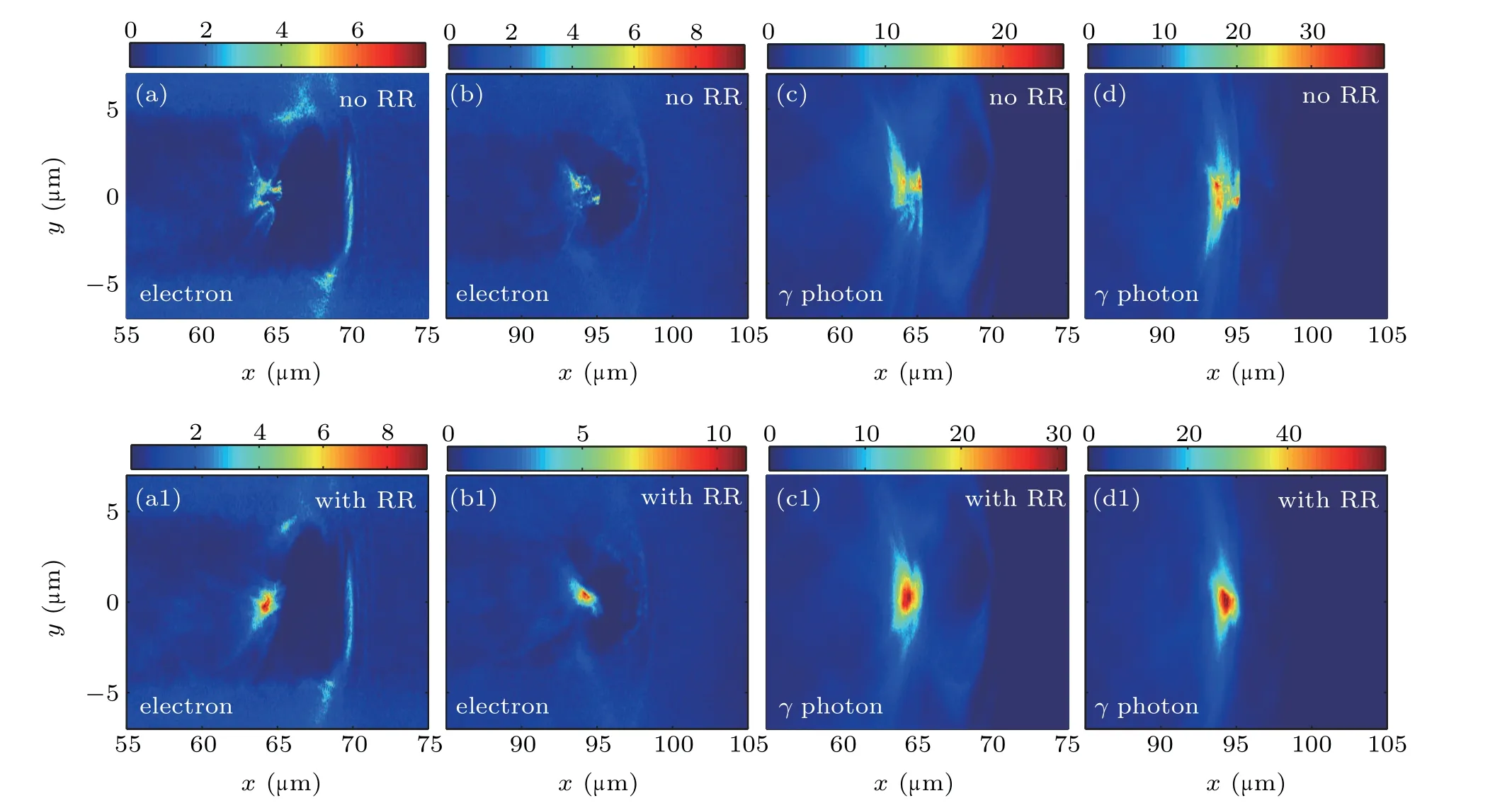
Fig.11. Distribution of electrons at t =250 fs[(a)and(a1)]and t =350 fs[(b)and(b1)]and of γ-photons at t =250 fs[(c)and(c1)]and t =350 fs[(d)and(d1)]without(top row)and with RR effects for the same laser and target parameters(target 3). Electron and γ-photon densities are normalized by the critical density nc.

Table 2. The Ne and Nγ are the number of electrons and γ-photons with energy of 1 GeV,Ee and Eγ are the cutoff energies of electrons and γ-photons,ηe and ηγ are the laser energy conversion efficiencies to electrons and γ-photons in the cases of laser intensities from a0=50 to a0=300(for LP laser with RR),CP laser(for a0=250 and with RR),and without RR(for LP laser and a0=250)at t=360 fs for target 3. The channel length and curvature radius are fixed to their optimal values.

6. Summary

An efficient scheme for the generation of ultrabrightγrays from the interaction of an intense laser pulse with an NCD plasma was studied by using a 2D-PIC simulation. When the intense laser propagates in the NCD plasma, some electrons are trapped in the channel by the self-generated magnetic field and the RR trapping effect and are accelerated to energies of several GeV in the first stage. High-energy, high-density ultrabrightγ-photons are emitted by nonlinear Compton scattering as the accelerated electrons collide with the reflected laser pulse in the second stage. The effects of target shape on the generation of brightγ-rays are investigated using three target configurations. Simulation results showed that the presence of a channel and the use of a curved foil target significantly affect the generation of low-divergence, high-energyγ-rays when targets 2 and 3 are used. For target 3, the beam quality of the accelerated electrons is improved, and the density ofγ-photons is 4.5 and 1.5 times higher than those for targets 1 and 2, respectively. The peakγ-ray brightness is 4.6×1026photons/s/mm2/mrad2/0.1%BW at 100 MeV. Furthermore,the optimal plasma channel length and curvature radius of target 3 for efficientγ-ray emission were also analyzed.The results indicate that the optimal channel length and curvature radius of target 3 areL=100µm andr=6µm,respectively.Finally,we investigated the effects of the laser polarization,laser intensity,and RR force onγ-ray emission. A comparison of LP and CP lasers revealed that the laser polarization strongly affects the electron acceleration and the generation of brightγ-rays. With increasing laser intensity, many electrons in the NCD plasma are trapped in the strong laser field region owing to the strong RR trapping effect and form an ultradense electron bunch. As a result, high-density ultrabrilliant GeVγ-rays can be obtained via Compton scattering.

Acknowledgment

The authors are particularly grateful to CFSA at the University of Warwick for allowing us to use the EPOCH code (developed under UK EPSRC Grants (Grant Nos.EP/G054940/1,EP/G055165/1,and EP/G056803/1)).