基于分时电价的电动汽车有序充电策略研究*

郭豪杰，崔双喜

（新疆大学电气工程学院，乌鲁木齐 830047）

0 引言

近几年来，随着化石资源的枯竭和环境问题的日益加剧，电动汽车作为一个新兴产业受到了广泛地关注，其中纯电动汽车（Electric Vehicle,EV）作为新能源汽车的代表，与传统的燃油汽车相比以电代油，具有诸多优点，如行驶成本低、温室气体排放少、噪声小、能量转化率高以及能源多样化等，因此，当今生态环境下，纯电汽车的投入可以缓解石油供给压力[1-2]并改善大气环境。

由于电动汽车产业具有的广阔前景，国内外研究人员对其相关的充电策略进行了大量深入研究。利用当前的分时电价政策，引导用户在电网负荷水平较低的时段进行充电，是电动汽车有序充电策略的基本思路。

电动汽车的充电策略按照调控方式来划分，主要包括集中式充电和分散式充电[3]。集中式充电是指电网公司或者第三方充电运营商对一定区域内接入的电动汽车的充电行为集中控制，进行统一地规划和安排，王株凝［4］采用日前充电调度的方法，基于用户的日平均负荷曲线和电动汽车日充电需求曲线对电动汽车的充电行为进行了安排，在常规情况下具有较好的优化效果，但当车辆的实际用车需求与预测需求差异较大时，优化效果不够理想。薛宇轩[5]以网损最小为目标函数提出实时充电策略，由区域内电网的实时负荷情况对电动汽车的充电行为进行安排，相较于日前充电调度，具有更好的整体优化效果。分散式充电方式，相对于无序充电而言，在降低电动汽车用户充电充电费用和电网负荷峰谷差方面有很好的效果。孙晓明等［6］基于拉格朗日松弛法提出了分散式有序充电策略，收敛速度受初值影响较大。吕仁周等[7]采用交替方向乘子算法，将优化目标函数转化为多个子优化问题在进行求解，优化时间不受优化规模的影响。分散式充电方式较集中式充电方式在运算效率方面有较大提升，但在平抑负荷波动方面存在一定不足。

按照优化层面可以分为用户层、充电桩层和电网层，张乐平[8]以电动汽车用户的充电费用最小作为目标函数，建立电动汽车有序充电模型。Rotering N等[9]采用动态规划法对电动汽车的充电时间进行优化，可以减少电动汽车用户的充电成本。徐智威等[10]在分时电价的基础上，以充电站的收益最大作为目标函数，建立电动汽车有序充电模型。葛文拖等[11]通过对峰谷分时电价的响应，以充电桩的利益最大为优化目标函数，建立电动汽车有序充电模型。俞子聪等[12]以峰谷分时电价为背景，电动汽车在负荷低谷时期进行充电，当负荷处于峰谷时期时电动汽车向电网馈电，以此来达到“削峰填谷”的目的，从而减小电网的负荷波动。王劲峰等[13]提出了基于遗传算法的电动汽车有序充电控制策略，以电网的负荷峰谷差最小为目标函数。汝改革等[14]以电网负荷的峰谷差最小为目标函数，提出了一种基础电价响应和电网激励的电动汽车有序充电控制策略，采用遗传算法对目标函数进行求解。Sortomme等[15]以电网负荷的方差最小为目标函数，建立有序充电模型，可以有效的抑制电动汽车充电过程中电网的负荷波动。

本文在以上研究的基础上，提出了一种以峰平谷分时电价为基础，以电动汽车用户充电费用最少和电网负荷峰谷差最小为目标的电动汽车有序充电策略，通过多目标遗传算法对目标函数进行求解。以某小区为例，通过仿真分析，可以得到该有序充电策略可以达到减小电网负荷的峰谷差的目的，验证了所提策略的有效性。

1 电动汽车充电建模

电动汽车的负荷模型主要取决于电动汽车用户的返回时刻、出行时刻以及日行驶里程。私家车每日行驶里程结束时刻的概率密度函数为：

式中：μs为每日行程结束时间的期望值，μs＝17.47；σs为每日行程结束时间的标准差，σs＝3.41。

私家车每日最早离开时刻的概率密度函数为：

式中：μe为用户每日最早离开时间的期望值，μe＝8.92；σe是用户每日最早离开时间的标准差，σe＝3.24。

私家车的日行驶里程概率密度函数为：

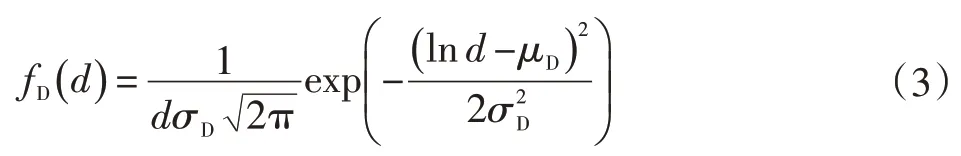
式中：σD为每日行驶里程的标准差，σD＝1.14；μD为每日行驶里程的期望值，μD＝2.98；d为每日行驶里程，km。

2 电动汽车无序充电模型

选取该小区的某一日作为仿真日，将该仿真日划分为等间隔的96个时段，每个时段的时间间隔为15 min，对仿真日内纯电动汽车EV的充电负荷情况采用蒙特卡罗法进行模拟分析。

根据EV行驶里程d和电池参数可以求出在返回时刻EV的荷电状态，得出：

式中：Si,star为充电开始时刻的荷电状态；Si,end为充电结束时刻的荷电状态；Bi为电池的容量；E100＝14，为百公里耗电量，kW·h。

第i辆电动汽车的充电时长如下所示：

式中：Pi为EV的充电功率，kW；Si,star为第i辆车返回时刻的荷电状态；Si,end为第i辆车结束充电时刻的荷电状态；Bi为EV的电池容量。

电动汽车入网后的总的负荷如下所示：

式中：zi为第i辆车在t时刻的状态，zi＝0表示当前时刻EV处于未充电状态，zi＝1表示当前时刻EV处于充电状态；p′n(t)为t时段小区的基础负荷。

基于蒙特卡洛法模拟EV无序充电的流程如图1所示。

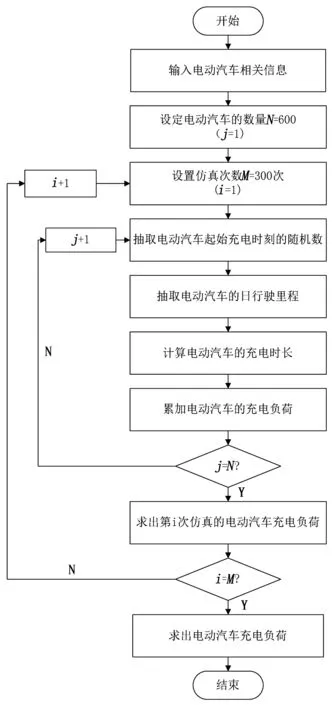
图1 EV无序充电流程Fig.1 Monte Carlomethod tosimulateelectric vehiclechargingflow chart

3 电动汽车有序充电模型

采用峰平谷分时电价，将一天划分为3个时段，峰时段（8:00—12:00，17:00—21:00）、谷时段（0:00—8:00）和平时段（12:00—17:00，21:00—24:00），分时电价如表1所示。

表1 分时电价政策Table.1 Time-of-usetariff policy

3.1 目标函数

为减小EV无序充电对电网造成的不利影响，提高电网的稳定性。本文采用峰平谷分时电价对EV用户的充电行为进行引导，提出了综合EV用户和小区电网两方面利益的多目标有序充电策略，以EV用户的充电费用最少和小区电网总的负荷峰谷差最小作为目标函数，建立电动汽车有序充电的优化模型。

（1）电网侧以总的负荷峰谷差最小为目标函数，即

（2）用户侧以EV用户的充电费用最少为目标函数，即

式（7）～（8）中：N表示EV的数目。

3.2 约束条件

（1）EV充电数量约束

式中：N为小区内总的EV数；n为当前处于充电状态的车辆数。

（2）结束时刻EV的荷电状态约束

（3）荷电状态约束

式中：S(t)为EV充电电量的荷电状态；Smax＝1，表示荷电状态最大值。

3.3 采用遗传算法对模型进行求解

遗传算法是一种通过模拟达尔文生物进化论的自然选择过程和遗传学的生物进化过程来求解最优解的方法[5]。EV有序充电涉及多个约束条件，多个非线性变量，多目标进行求解，需要有较强的鲁棒性和全局搜索能力。故本文采用多目标遗传算法对搭建模型的目标函数进行求解，具体流程如图2所示。

图2 算法求解流程Fig.2 Multi-objective genetic algorithm solution process

4 算例分析

4.1 数据及参数设置

小区内EV有600辆，电池容量为43 kW·h，充电方式为慢速充电，充电功率为3 kW。该小区原始负荷曲线如图3所示。

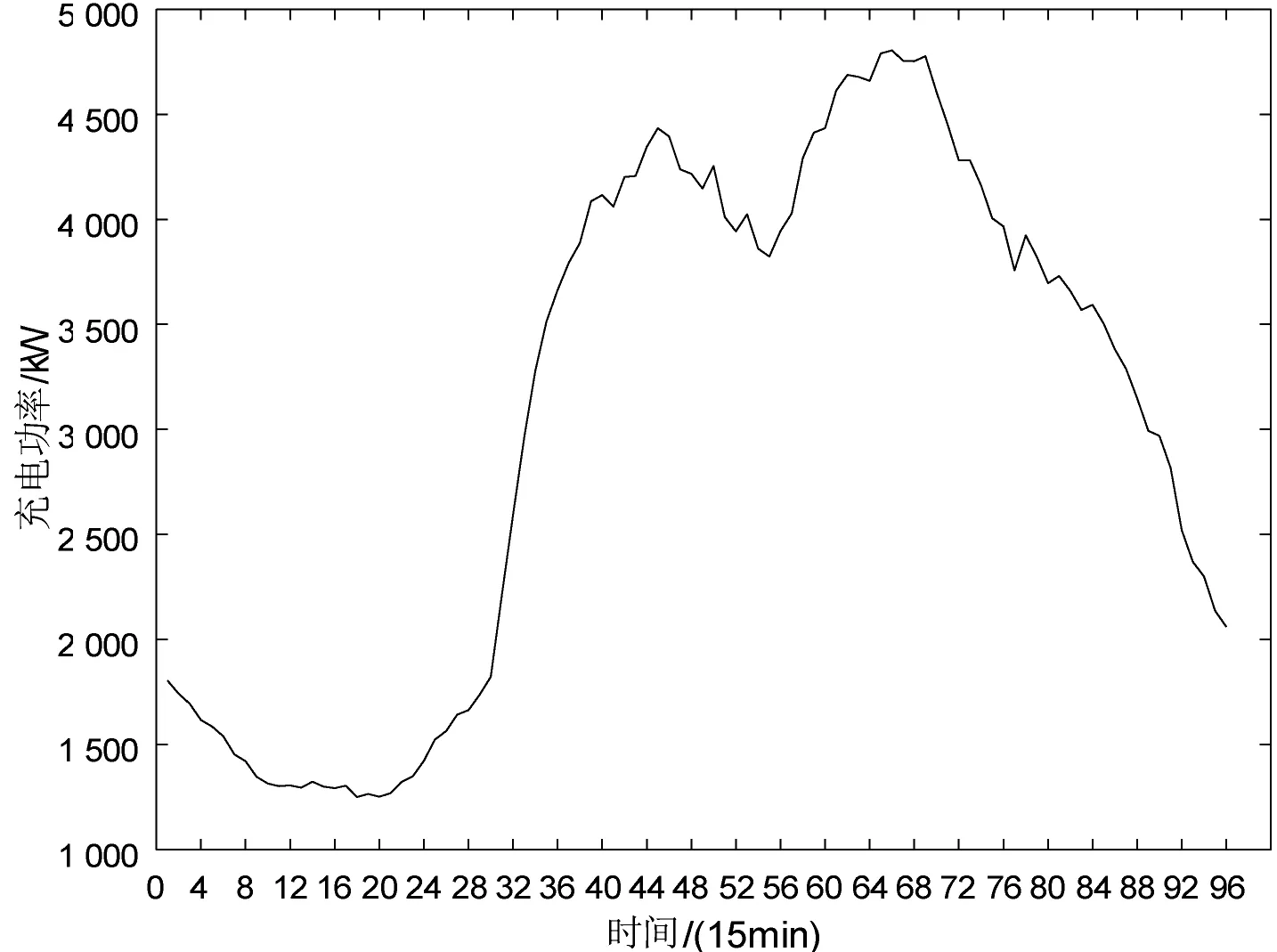
图3 小区原始负荷曲线Fig.3 Theoriginal load curveof thecell

4.2 仿真结果及分析

4.2.1 EV无序充电仿真结果

根据图1所示流程，模拟该小区600辆EV无序充电策略下的充电负荷，仿真结果如图4所示。从图中的仿真结果可以看出，EV在无序充电策略下主要集中在小区负荷的高峰时段进行充电，当小区负荷与EV的充电负荷进行叠加会造成负荷峰值的加剧，从而加大小区负荷的峰谷差，不利于该小区电网的安全稳定运行。因此，有必要对EV用户的充电行为进行引导和规划，合理地规划其充电负荷，以此来提高电网的稳定性，保证电网运行的安全性。

图4 无序充电的负荷曲线Fig.4 Load curveof random charge

4.2.2 EV有序充电仿真结果

在峰平谷分时电价的基础上，以电动汽车用户充电费用最少了和电网的负荷峰谷差最小为目标函数，建立电动汽车有序充电控制模型。仿真结果如图5所示。从图中可以看出，本文提出的以峰平谷分时电价为基础，以EV用户充电费用最少和小区电网负荷峰谷差最小为目标函数的EV有序充电策略，由于并未增大负荷的峰值，并不会导致电网负荷峰值的加剧。

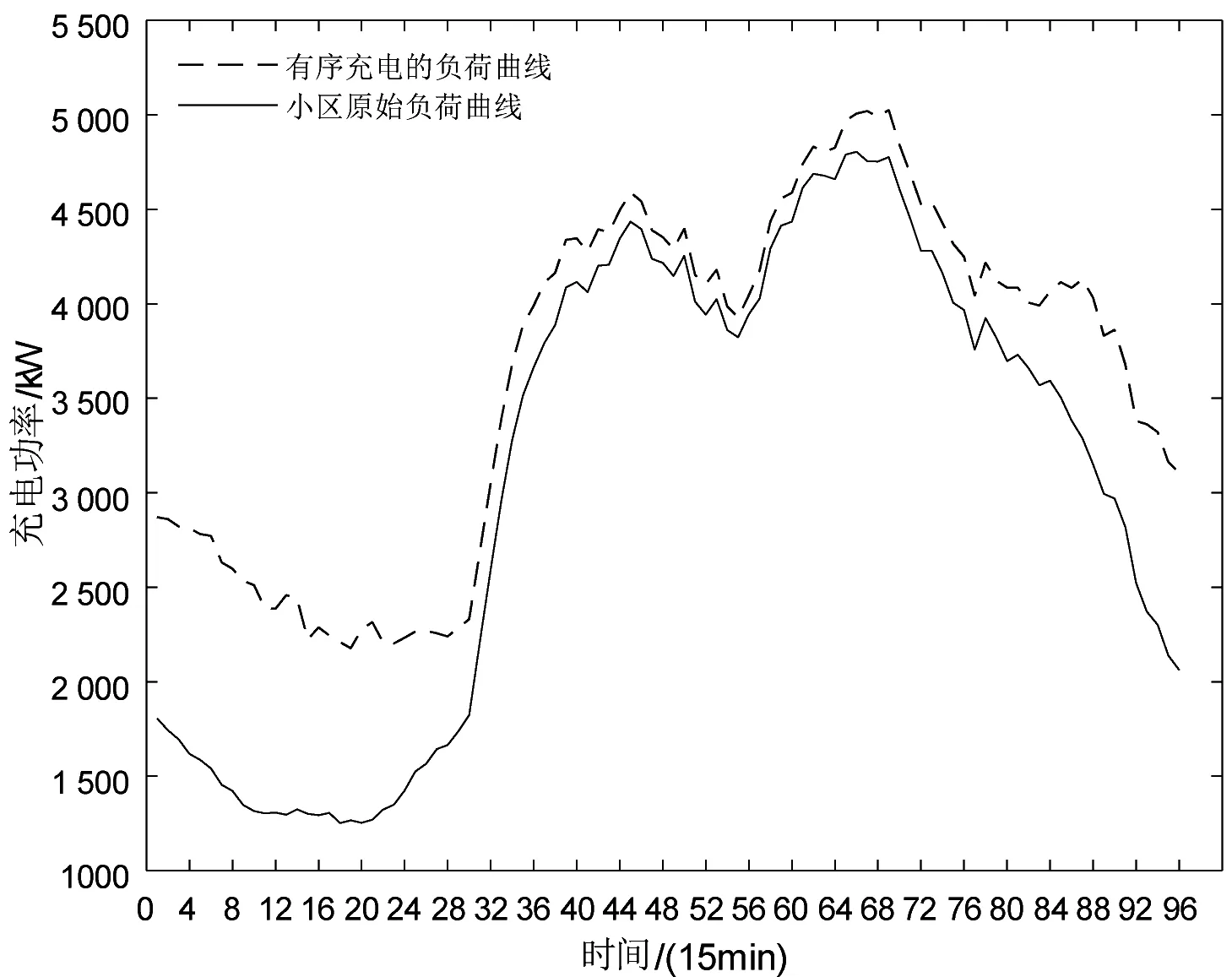
图5 有序充电负荷曲线Fig.5 Order chargeload curve

EV优化前后负荷变化的仿真结果如图6所示，图中可以看出，电动汽车在无序充电策略下进行充电时，充电负荷曲线与小区电网的基础负荷曲线比较相似，负荷的高峰时段重合，造成负荷峰谷差加剧。通过本文提出的有序充电优化模型，将电动汽车的充电负荷从负荷高峰时段转移到负荷低谷时段，负荷的峰值并无变化，但是负荷谷值明显增加了，进而缩小电网的负荷峰谷差，证明了本文所提策略的有效性。

图6 优化前后负荷曲线对比Fig.6 Load curvecomparison before and after optimization

5 结束语

本文在峰平谷分时电价的基础上建立了以电动汽车用户充电费用最少和电网总负荷峰谷差最小为目标函数的电动汽车多目标有序充电策略。针对本文提出的多目标函数和约束条件，采用多目标遗传算法对目标函数进行求解，仿真结果表明：电动汽车多目标优化策略，在总负荷峰谷差方面有很好的优化效果，能够减小小区电网总的负荷峰谷差，证明了该策略是行之有效的。由于峰平谷电价按一日内时间分成了峰时段、平时段和谷时段3种电价，不能很好地反映一日内负荷变化的动态特点，因此希望后续可以进一步对EV的充电电价进行研究，以制定更加合理的有序充电策略。