基于随机矩阵理论的配网多区域异常定位方法研究

上海电力设计院有限公司 秦嘉南

配电网具有节点众多、运行方式灵活、设备运行环境恶劣等特点。据统计电力系统80%以上的故障都来源于配网[1]。由于配网深入城市腹地、人类活动更加频繁，更易受到人为因素干扰，给测量装置和电力通信设备都带来远超输电网络的影响，很多高电压输电侧异常检测与定位方法在配电网都难以发挥预期效果[2-3]。在现有配网故障定位研究中，对于不同类型配网异常都取得相应的检测和定位成果，但都存在一定缺陷与不足，很少研究多区域异常的检测与定位。

1 PMU量测数据矩阵构建与处理

1.1 原始矩阵获取

在配网PMU量测系统中，在保持电网可观测性的前提下，在配网中的不同位置安装个PMU量测装置，每个量测装置检测的信号维数为，PMU采样频率为，由PMU采集的数据通过滑动窗口的形式形成原始数据矩阵（图1）。

图1 滑动窗口示意图

采样数据矩阵的宽度反映一个矩阵中包含信息在时间上的跨度，其大小不能超过异常状态的持续时间，假设采样时间为，则采样数据矩阵的宽度。根据奈奎斯特采样定律，采样时间不应超过故障持续时间的一半。如，配电网发生单相接地故障的持续时间为，则应满足。本文中PMU采样频率设定为，则采样数据矩阵的宽度就需满足。滑动时间间隔会对检测精度产生影响，越小异常检测精度越高，单位时间内产生的矩阵数量越多，数据处理的速率也会明显减缓，从而影响异常检测的时效，所以的取值需在精确性和快速性上进行一定取舍。

1.2 采样矩阵处理

2 基于高维协方差矩阵的多区域异常源数目检测原理

2.1 高维协方差矩阵的异常检测原理

假设矩阵YN×L为PMU量测数据经过标准化后得到的数据矩阵，此时系统正常稳定运行，矩阵为矩阵YN×L的样本协方差矩阵，当时，根据随机矩阵理论，用a、b表示矩阵的最大特征值和最小特征值的极限值，则有式中为噪声的方差。

2.2 基于序贯检测的多区域异常源检测步骤

为实现配电网中多个异常源的检测，假设异常源的数量为p，在上述方法中加入序贯检测思想，进行多区域异常源的检测。从样本协方差矩阵中删除前p-1行和前p-1列，其中p的取值范围为(1,min(N,L)-1)，将降阶后得到的子阵分别记为。将的特征值按照降序排列，则第p个异常源的检测统计量为：

因此第p个目标的检测的阈值为：

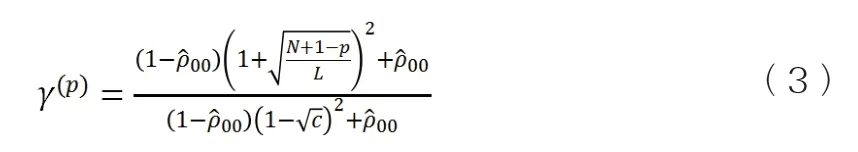
综上，当p的取值从1开始增长到min(N,L)-1，不断比较检测统计量T(p)和检测决策阈值γ(p)，直到检测统计量不再超过决策阈值为止，用公式表示即为Presult=arg max(P){T(P)〉γ(P)}，从而实现多故障源数目的检测：初始化条件，获取随机矩阵的协方差矩阵，并假设p=1；由式（2）和式（3）分别计算出检测统计量T(p)和检测阈值γ(p)；比较检测统计量和检测阈值，判断p第个异常源是否存在；若第p个异常源存在，则取p=p+1，在样本协方差矩阵估计中删除前p行和前p列、返回第二步重新计算，若第p个异常源不存在则进行下一步；检测结束，确定故障源数目为p-1个。

3 算例分析

本文使用PSCAD软件搭建了IEEE39标准节点的电力系统仿真模型，并根据电网可观性进行PMU优化配置，在39节点仿真模型中配置了18个PMU量测装置，IEEE39节点拓扑结构以及PMU节点分布如图2所示，其中方框为PMU量测装置。

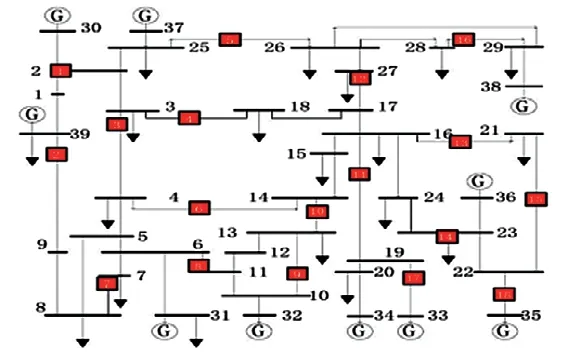
图2 IEEE39节点及PMU分布拓扑图

仿真模型运行环境为10kV低压配电网，变电站均使用110kV变电站并假设为无穷大电源系统，我国低压配电网采用中性点不接地方式，仿真模型中也将在低压侧使用中性点不接地方式，变压器高压侧则采用经消弧线圈接地方式。本文将配电网中故障分为两类，一类是以单相接地、单相断线为代表的弱故障，该类故障有相对明显的异常信号，故障持续时间也较短，故障影响范围也较小；另一类为强扰动，通常具有持续时间长、影响范围大的特点，如谐波超标、低频振荡等。

在IEEE39节点系统加入两个三次谐波异常源，THD为5.625%超标谐波，异常持续时间为0.1s，两个谐波源的位置分别为IEEE39节点拓扑中母线16与母线21之间的LN23、母线4与母线14之间的LN8。当仿真时长达到1s时，位于母线16至21之间以及母线4至14之间的两个三次谐波源接入仿真电路，基于序贯检测后将本算例中T、T(2)、T(3)及其对应阈值的仿真数据绘制成图3、并可观察到：样本矩阵和一阶子矩阵的检测统计量都超过了阈值，而二阶子矩阵未超过阈值，说明当去除前两个异常源后二阶子矩阵已不呈现异常状态，从而可判断此时配电网存在两个异常源。

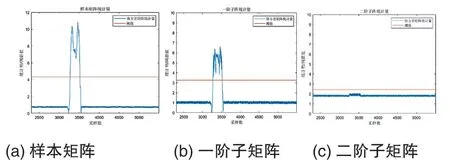
图3 样本协方差矩阵的检验统计量

利用主成分分析法进行故障定位，选取故障发生前4个与故障发生后6个等间隔的滑动窗口，并取用于重构数据的主成分数量为2、即k=2，计算其各个PMU量测变量对主成分的因子载荷，并通过得分进行排序。当故障发生后主成分累计贡献率有显著提升。故障发生前PMU各量测值的得分排序也是随机分布的；而故障发生后，本例中位于样本矩阵的61、49、68、45列的数据得分明显上升。经PSCAD软件的目录检索，故障发生后得分上升明显的信息量来自于6号PMU、13号PMU等。

将故障发生后滑动窗口构建的共计200个样本矩阵进行整理，将得分排序前10的PMU在这200个滑动窗口中的出现频次进行统计，再将故障发生时各PMU在得分体系下的得分整理，其中前六名的PMU编号、计数（次）、比率（%）、得分分别为6/200/100/1.548、13/200/100/1.541、12/197/98.5/0.858、9/171/85.5/0.845、1/166/83 /0.847、3/152/76/0.672，由此可知6号、13号、12号PMU出现的频次最高，6号和13号PMU得分远高于其他PMU。说明其在故障后长时间、高相关性地影响着协方差矩阵的主成分，从而可以判定6号和13号PMU量测装置的位置最接近异常点。因此在该仿真环境下配电网中共有2个故障源，故6号和13号PMU即为故障源定位结果，与仿真设置值一致，验证了本文提出基于随机矩阵理论的配网多区域异常定位方法的有效性和针对不同类型故障的通用性。