利用频率定义推导多普勒效应公式
杨军伟
(浙江金华第一中学 浙江 金华 321015)
多普勒效应首先由奥地利物理学家多普勒研究,发现波源与观察者互相靠近或者远离时,接收到波的频率会发生变化.本文通过频率定义导出波源频率与观察者接收到的频率之间的关系,得到多普勒效应的定量公式.
1 非相对论情形下多普勒效应公式
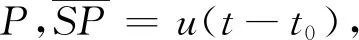
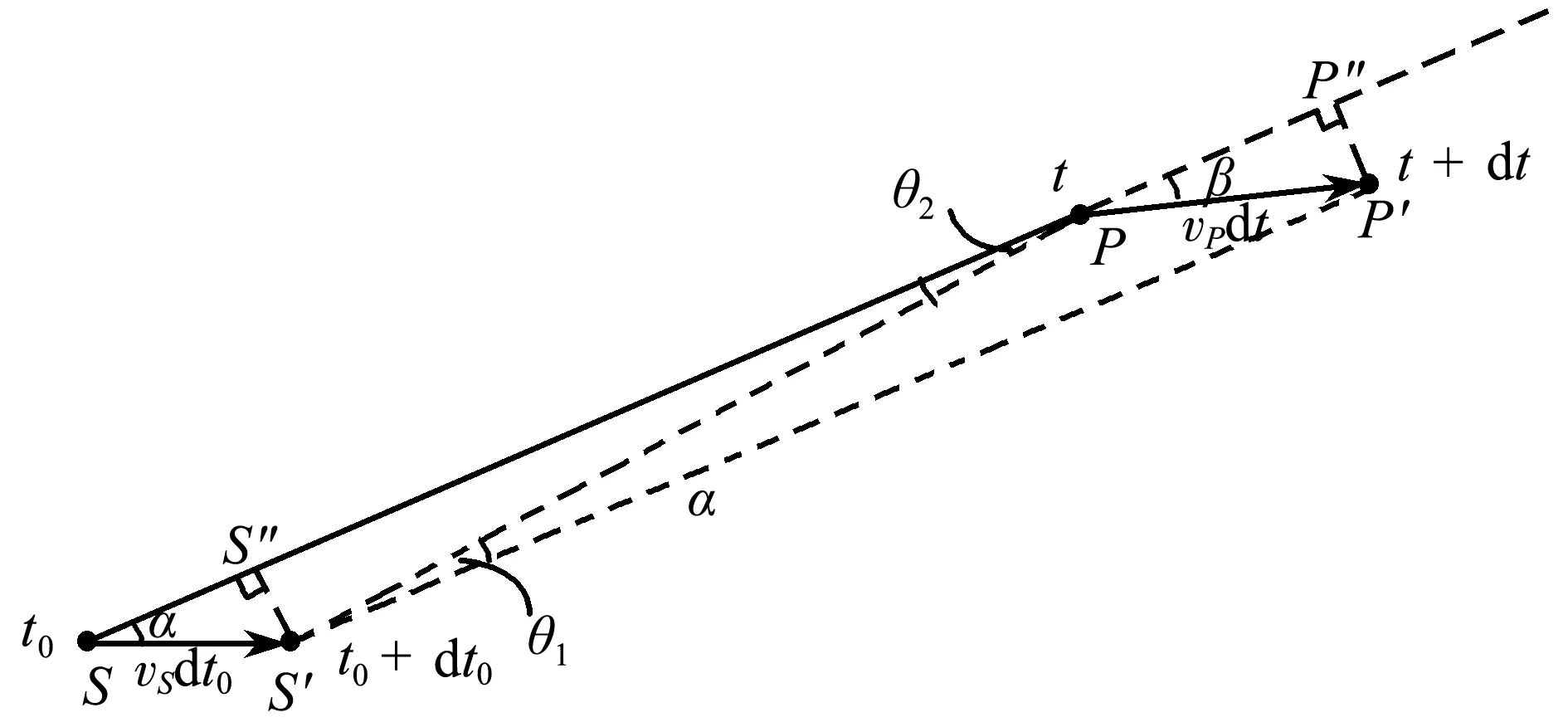
图1 推导多普勒效应公式示意图
由几何关系得
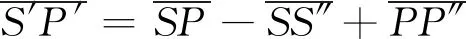
u[(t+dt)-(t0+dt0)]=u(t-t0)-vSdt0cos α+vPdtcos β
(1)
式(1)整理得
(u-vPcosβ)dt=(u-vScosα)dt0
(2)
根据频率定义,波源发出波的频率和观察者测得波的频率分别为
(3)
式(2)、(3)联立可得
(4)
式(4)即为非相对论情形下多普勒效应公式.
在应用式(4)直接观察者感受到的频率时,特别注意SP为不同时刻的波源与观察者位置,因为α,β并不能直接从初或末时刻获得,从而导致在很多情形下直接应用公式并不方便.反而从式(4)推导的基础,即频率的定义出发,倒不失一般性,且方便.譬如如下实例场景.
【实例】(第22届全国中学生物理竞赛复赛试题)如图2(a)所示,两辆汽车A与B,在t=0时从十字路口O处分别以速度vA和vB沿水平的、相互正交的公路匀速前进.汽车A持续地以固定的频率ν0鸣笛,已知声速为u,且有u>vA,vB,求解任意时刻汽车B的司机所检测到的笛声频率[1].

(a)
解析:如图2(b)所示,t时刻时笛声传播到汽车B,汽车B位于B(t)处,距O点的距离为vBt.汽车A发出此笛声时为t0时刻,位于A(t0)处,距O点的距离为vAt0.此笛声由发出点到接收点(t时刻B车所在点)所传播的路程为u(t-t0),由几何关系可知
(vBt)2+(vAt0)2=[u(t-t0)]2
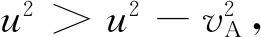
解得
两边取微元
因此
2 相对论情形下多普勒效应公式
(5)
根据式(2)、(5),得
注:式(2)中u为介质中的光速,因此
(6)
式(6)即是相对论情形下多普勒效应公式,其中α,β为介质参考系中光源发出光时其速度与发光方向的夹角,观察者接收光时其速度与光束的夹角.
同样我们可以依照式(6)推导过程来解决如下问题.
问题:如图3所示,惯性系中的宇宙飞船A,B同时从P处出发,A沿直线lA方向以匀速度vA运动,B沿直线lB方向以匀速度vB运动,直线lA与lB的夹角为锐角φ,两者在两直线交点P同时出发之后,A向对方连续地发射本征系计时系统频率为ν0的球面光波.对方B可连续地接收到光波.考虑相对论效应,探讨B于固有时时刻τB接收到的频率νB(τB)[1].
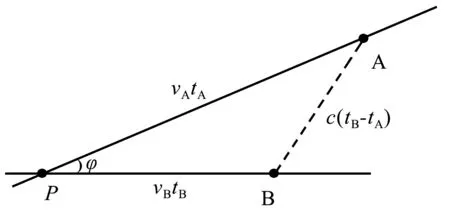
图3 宇宙飞船发射信号接收信号过程
解析:由几何关系可得
(vAtA)2+(vBtB)2-2vAtAvBtBcosφ=
[c(tB-tA)]2
解得

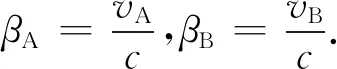
对上式两边微分得

根据频率定义
综合解得

3 结束语
多普勒效应在生产生活中有非常重要的应用,从频率定义出发,我们可以从本质上去理解多普勒效应的实质,更加深刻地理解其机制.

