利用最小二乘法拟合水位流量关系曲线探讨
王 伟,蔡文生,邓 科
(江苏省水文水资源勘测局徐州分局,江苏 徐州 221000)
1 引言
水位流量关系曲线是用来描述测站基本断面的水位与通过该断面的流量两者之间关系的曲线。对于给定的水位和流量数据,由于受变动回水与洪水涨落等因素的影响,因此数据本身并不一定可靠,个别数据的误差可能比较大,从一堆看上去杂乱无章的数据中找出一定的规律,即设法构造一条曲线,能够比较真实地反映水位与流量之间的关系,常用的方法是构造两者之间的关系式[1],通过相关关系拟合曲线,并求出相关方程式。
当前,多数地区多采用人工定线,通过实测的流量资料,反复修正后编制水位流量关系结点进行推求流量。传统的人工定线工序繁多,需反复计算,同时受人的经验影响较大,不同的人定出不同的关系线,有较大的主观性,定线任意性大[2]。利用MATLAB拟合语句,不仅能实现对水位流量曲线的拟合,而且曲线完全按照设定的数学模型拟合,优选好参数后,通过程序运算得到最终的曲线及曲线方程,避免了人的主观性。随着当前水文信息化水平的不断提高和计算机技术的普及,利用最小二乘法对水位流量曲线拟合将是对水文信息进行处理的重要途经,对开展流量自动测报和水文站无人值守工作具有重要的应用价值。
2 最小二乘法拟合原理
最小二乘法是通过最小化误差的平方和寻找数据的最佳函数匹配,只要求拟合的曲线合理的反应数据的基本趋势,而并不要求曲线一定经过每个数据点,被视为从一组测量值中求出一组未知量的最可信赖的方法之一[3],利用最小二乘法可以简便的求得未知数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
从数学上讲,最小二乘法就是寻找与给定点(xn,yn)(n=1,2,…,m)的距离平方和最小的曲线g(x)。g(x)称为拟合函数或者最小二乘解,求解拟合函数g(x)的方法就是曲线拟合的最小二乘法。本文将其应用于水位流量的关系曲线拟合,具体原理如下:

设某函数的线性组合为:其中f1(x),f2(x),f3(x)…fn(x)为已知函数,c1,c2,c3…cn为待定系数。

其中
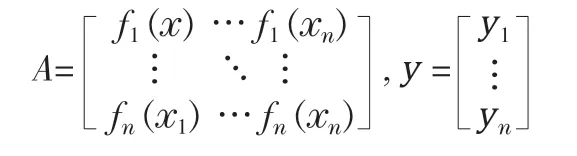
且c=[c1, c2…cn]T
该方程的最小二乘解为c=A/y,将c值代入到方程(1),即可得到相应多项式拟合方程。
3 实例分析
现以某实用堰闸站2018 年、2019 年、2020 年25 组实测水位流量数据为例,应用本文提出的最小二乘法原理进行曲线拟合,并对其进行“三项检验”。根据《水文资料整编规范(SL 247-2012)》中堰闸站推流规定,堰闸站自由孔流流量计算公式为:

式中:Q为流量,m3/s;Mi为流量系数;B为闸门总宽或开启净宽,m;e为闸门开启高度,m;hu为上游水头,即上游水位减去闸底高程,m[4]。
堰闸站自由孔流流量相关关系为e/hu-Mi,通过实测流量,计算流量系数Mi,确定e/hu与Mi关系函数模型,并求出相关函数方程,率定出拟合曲线图,据此推流。将整理好的25 组相关关系e/hu-Mi数据导入MATLAB,得到散点图见图1。
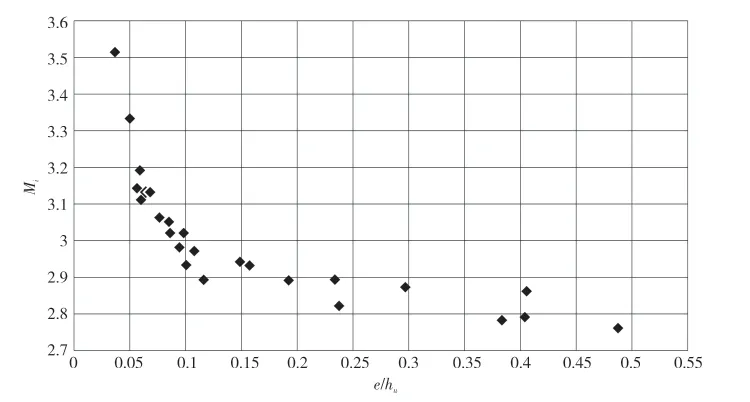
图1 e/hu-Mi数据散点图
常见的几种拟合曲线函数模型有幂函数y=axb+c、指数函数y=a﹡ebx+c、y=a﹡ebx+c﹡edx、双曲线函数及对数函数y=alnx+c,其中a、b、c、d为常数,x、y为变量。观察图1,根据e/hu-Mi点分布规律,与上述几种数学模型的曲线图比较,可以发现指数函数模型与相应关系点的走势比较吻合。比较y=a×ebx+c与y=a×ebx+c×edx两种指数函数模型,y=a×ebx+c使用拟合出的曲线,在闸门开启高度e不变的前提下,上游水位越低,e/hu值越大,拟合出的曲线与实际测量值的变化趋势一致;反之当上游水位较高时,拟合出的曲线基本呈现平行状态,与实测值误差较大;相比较y=a×ebx+c×edx在上游水位较高时能更好地反映e/hu-Mi点的趋势。因此,选择y=a×ebx+c×edx函数模型对测量数据进行曲线拟合,得到拟合曲线图。
观察拟合曲线图,找出并剔除偏离较大的e/hu-Mi点,进一步优化拟合曲线。运行相关程序,求解函数模型的待定系数,得a=2.385,b=-40.51,c=2.974,d=-0.1456,统计系数SSE=0.02699,RMSE= 0.03585,R-square= 0.9639。将a、b、c、d的值代入函数模型,得到关于e/hu-Mi的拟合方程(4)及其曲线图,见图2。
通过计算得到对象要素的缺省度为51%,环境要素的缺省度为73%,时间要素的缺省度为75%,由此可看出,环境要素和时间要素的缺省程度较大.但这里对对象要素的统计没有区分主体与客体,不能准确表示对象要素的缺省度,所以又对主体与客体的数量进行了统计,如表6所示.
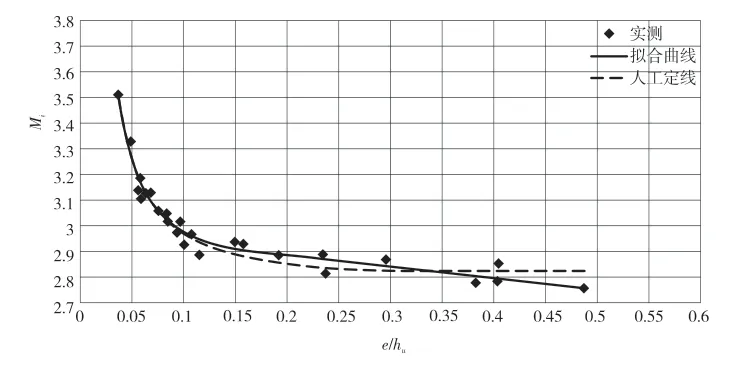
图2 e/hu-Mi关系曲线(由孔)
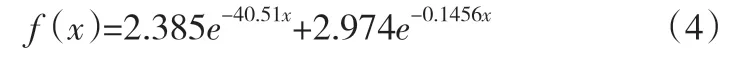
SSE(和方差)越接近于0,说明模型选择和拟合更好,数据预测也越成功;RMSE(均方根)也叫回归系统的拟合标准差,表示预测数据和原始数据对应点误差的平方和的均值的平方差;R-square(确定系数)的正常取值范围为[0,1],越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好。
将方程(4)带入方程(3)得到流量拟合方程

4 成果检验
4.1 三项检验
稳定的水位流量关系曲线及经单值化处理的单一线,均应计算关系点对关系线的标准差和随机不确定度,且测点在10个以上者,还需要对其进行符号检验、适线检验和偏离检验,以判断能否用于流量推算[4]。在此基础上,将实测的e/hu值代入拟合方程,计算相应地流量系数Mi,并对计算结果检验,是否符合相关规范要求。拟合曲线流量检验计算表见表2,检验结果见表3。
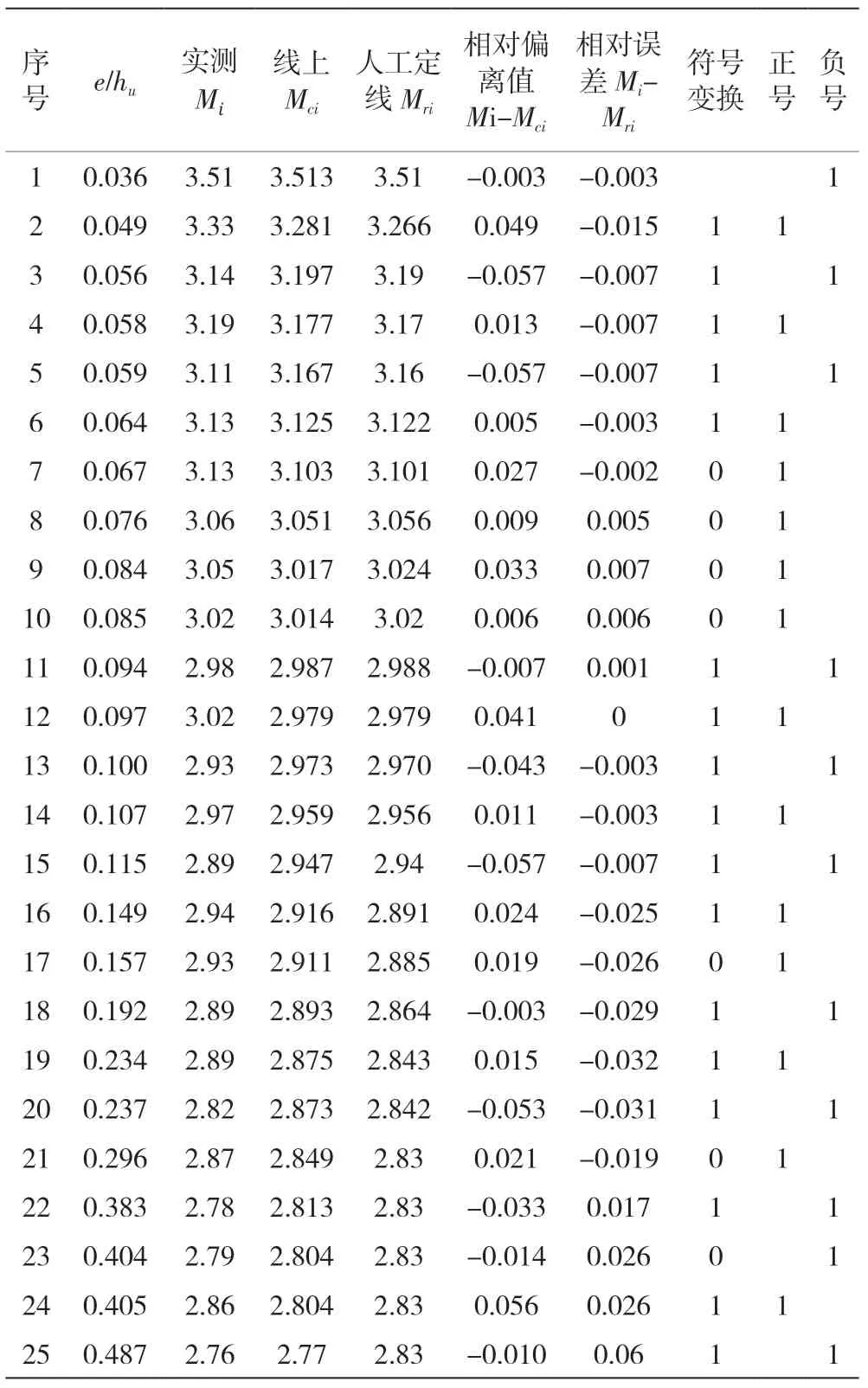
表2 某闸站水位流量拟合曲线检验计算表
(1)符号检验
偏离曲线正号个数K= 14(负号个数 11),n=25。
统计量:
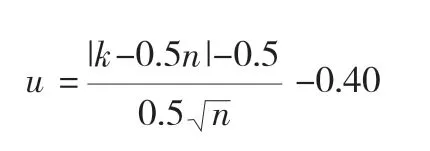
取显著性水平α=0.25,查流量整编规范中表2.4.1-1得1-α/2= 1.15与 比较, <1-α/2 ,则接受假设,定线合理。
(2)适线检验:
统计符号变换次数K=14,因K>0.5×(25-1)=12,此线免做此检验。接受假设,定线合理。
(3)偏离数值检验:
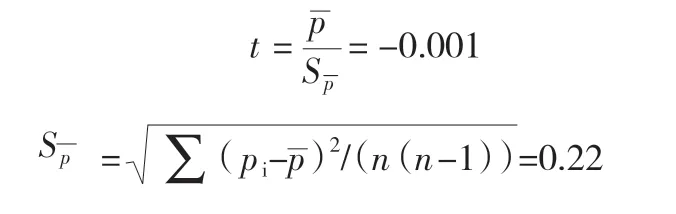
取显著性水平α= 0.20,查流量整编规范中表2.4.1-2得t1-a/2= 1.31与|t|比较|t| 表2 月潭水库下泄流量控制方案二 单位:m3/s (4)定线精度计算 为了进一步对曲线拟合成果进行分析,将拟合成果与人工定线成果进行对比分析,以人工定线成果为标准值,计算相对误差,统计结果见表2。从表2 中可以看出,除在高水位区域相对误差加大外,人工定线与利用MATLAB函数拟合成果误差都较小。分析其在高水位区域误差较大的原因是在高水位区域,实测流量数据较少,人工与函数都不能对曲线走势进行科学的控制,因此,人工定线与计算机定线都有较大任意性。从图2 中也可以看出,在低水位实测点较多区域,人工定线与函数拟合曲线几乎重合,且与实测点也大部分重合,随着水位增高,加之实测点变少,人工定线部分近乎与水平轴平行,其相对误差要比拟合曲线误差偏大。 (1)通过对拟合出的曲线进行“三项检验”,结果表明,使用最小二乘法拟合出的水位流量关系曲线,符合三项检验及标准差的定线标准,且精度完全符合相关规范要求,可以用于流量预报以及水文资料整编。 (2)上述检验与实例应用结果显示,确定好相关系数后,应用最小二乘法可以很容易实现对水位流量关系曲线的拟合,而且操作人能根据拟合成的曲线与实测点位置的偏离程度,实时剔除偏差较大的点,避免了人工定线时反复计算的麻烦。曲线完全按照给定的数学模型拟合,避免了人的主观性,提高了定线精度与效率。 (3)水位流量关系线或系数线分析定线工作,是测报方式改革的最基础的环节,直接影响自动测报工作资料精度。因此,选择合理高效的率定水位流量曲线的方法,对开展流量自动测报和水文站无人值守工作具有重要的实用价值,同时,也对水文事业走向现代化,提高社会对水文工作认可度具有重要意义。 (4)此次拟合曲线使用的数据偏少,尤其是高水位流量数据,不同水位测流次数、相同水位测流次数都比较少,可能会造成拟合出的曲线方程与高水位实际流量有较大偏差。因此,在以后的工作过程中,必须加强与水利部门的沟通与协作,抓住机遇,抢测高水位流量,完善水位流量基础数据,增加拟合方程的精准度。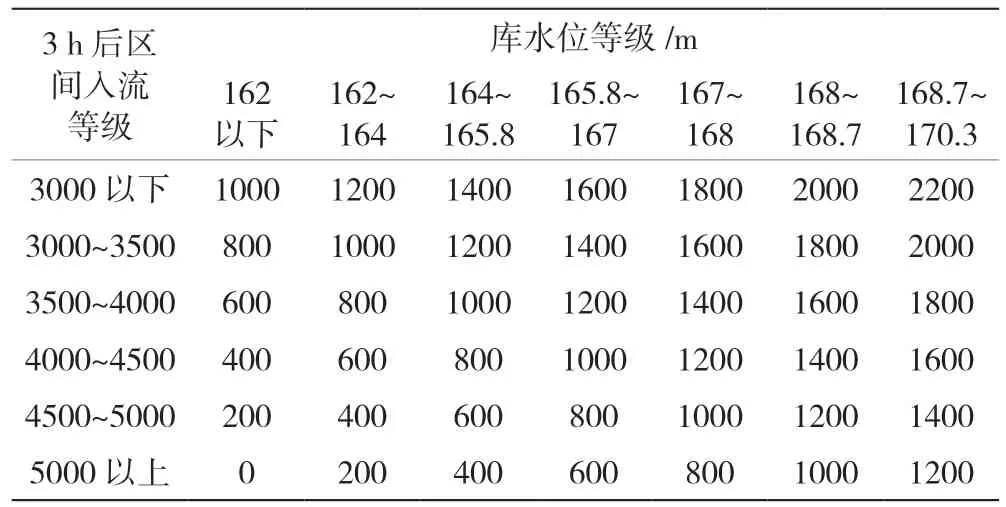
4.2 定线比较
5 结论与建议

