基于比例故障率模型的柴油发动机视情维修决策

王海龙， 张 营， 左付山

(南京林业大学汽车与交通工程学院， 南京 210037)

柴油发动机作为汽车的动力部件，其结构复杂，运动部件多的特点，使得柴油机维修诊断较为困难。目前，对于车辆柴油机的维修主要采用定时维修和事后维修的策略，定时维修具有容易执行等优点，然而并没有考虑发动机当前运行状态；事后维修则是在故障发生之后再进行相应的维修，维修成本高，经济损失大。为了提高经济效益和社会效益，避免维修不足或者维修过度，相关学者提出了视情维修。视情维修是通过监测设备的状态参数来反映设备的性能状态，然后根据相应的状态在故障发生之前采取一定的维修措施[1]，其最主要的就是建立设备运行状态参数与设备完好程度之间的对应关系[2]，建立模型的方法包括基于设备可靠性、概率性以及卡尔曼滤波等建模方法。

董思辰等[3]选择振动信号中的冗余参数作为协变量，利用威布尔比例故障率模型(Weibull proportional hazards model，WPHM)进行齿轮箱的运行可靠性评估，得到可靠度衰减时间与振动信号故障时间相近。刘璐[4]选择航空机载设备电机轴承的振动信号，通过特征提取后，基于WPHM进行了其可靠性评估和寿命预测。蒋文博等[5]提出了一种基于比例风险模型与机器学习的混合方法，有效的预测了电梯的剩余寿命。通过上述的研究发现，对于机械设备来说，WPHM能综合考虑设备运行状态及工作时间，有效反映设备的状态好坏，从而实现寿命预测与视情维护，因此柴油机作为机械设备，状态参数复杂并且维修决策较为困难，通过建立WPHM进行视情维修将减少大量维修成本并且提高工作效率。

综上所述，构建一种基于威布尔比例故障率模型的发动机视情维修策略，首先对监测到的柴油发动机在各个阶段的润滑油金属含量数据进行了主成分分析(principal component analysis，PCA)数据降维并通过极大似然估计求出了所建立的模型参数；为综合考虑成本和可用度，采用最小维修成本和最大可用度的综合维修策略，求得相应的最优预防时间间隔以及失效率阈值，从而根据当前监测到柴油机金属含量数据判断是否需要对其进行预防性维修。

1 威布尔比例故障率模型

1.1 比例故障率模型

比例故障率模型前期主要应用于医学领域[6]，其综合考虑了设备运行时间和当前状态信息之间的关系[7]，从而实现了对于设备健康状况的评估。该模型的性质是不同个体的故障率函数成比例[8]，并且故障率函数不随时间t的变化而变化。其基本形式为

h(t;Z)=h0(t)exp(rZ)

(1)

式(1)中：h(t;Z)为故障率函数；h0(t)为基本故障率函数，只与时间有关[9]；rZ=r1Z1+r2Z2+…+rpZp，Z为协变量，反映装备运行状态，按作用可分为外部协变量与内部协变量[10]，如振动幅度、金属含量等，r是协变量系数，反映了与之对应的协变量对装备故障率影响的严重程度[11]，ri的值越大，表明对应的协变量对故障率函数影响越大。

1.2 威布尔比例故障率模型的建立

在汽车可靠性研究中，指数分布、威布尔分布、正态分布、对数正态分布等都是较为常用的理论分布类型。由于柴油发动机为机械部件，一般机械部件的故障数据分布规律均服从威布尔分布，同时其对各种类型的数据具有很强的拟合能力，所以应用广泛，因此上述基本故障率函数选择较为经典和简单的两参数威布尔分布故障率函数作为比例故障率模型的基础函数[12]，两参数威布尔故障率函数具体形式为

(2)

式(2)中：β为形状参数，可改变曲线的陡峭程度；η为尺度参数[13]，可改变曲线中心线位置。

由此，得到了威布尔比例故障率函数[14]为

(3)

故障概率密度函数f(t)、可靠度函数R(t)以及故障率函数h(t)定义如下：f(t)是指所有部件在时间间隔(t，t+Δt)内发生故障的个数占总数的比例；R(t)是指规定时间内完成规定功能的概率，即部件寿命T大于某一时刻t的概率；h(t)是指定义为时间(0，t)内不发生故障的条件下，下一个单位时间(t+Δt)内发生故障的概率。由此，可以得到[15]

(4)

(5)

(6)

式中：N为部件总个数；n(t)为到t时刻发生故障的个数。

对式(6)左右两边同时在0～t上积分，得可靠度函数R(t)，即

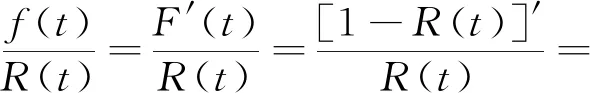
(7)

(8)

同理可得，相应的威布尔比例故障率可靠度函数R(t;Z)为

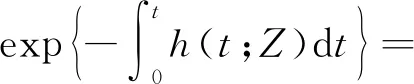
(9)

1.3 模型参数求解

为了通过威布尔比例故障率模型进行柴油发动机的可靠性评估，最关键的是对于模型中的三个参数进行求解β、η、r。对于三个参数估计的方法主要有最大似然估计法、最小二乘法、矩估计法、区间估计法等。由于极大似然估计法对于设备的不完全寿命数据是处理具有独特的优势，使得模型更加精确，因此本文中选择极大似然估计法对于模型的三个参数进行估计。

极大似然估计的基本原理是通过估计的参数使得样本出现的概率更大，似然函数的一般形式为

(10)

针对威布尔比例故障率模型，需要通过极大似然法求解，即求参数θ=(β，η，r1，r2，…，rp)何值时，使得似然函数的值最大。根据柴油发动机的失效密度函数f(t;Z)=h(t;Z)R(t;Z)，威布尔比例故障率模型似然函数为

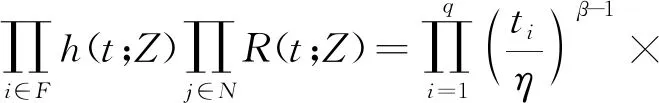
exp(rZ)dt]}

(11)

式(11)中：F为所测数据中故障集；q为故障数据个数；N为数据总集。

为了求得似然函数的最大值，需要先对其进行取对数，得到对数似然函数，然后分别对于β、η、r进行一阶求偏导并令其等于0，可以得到对数似然函数方程组。似然函数及其一阶方程组[16]为

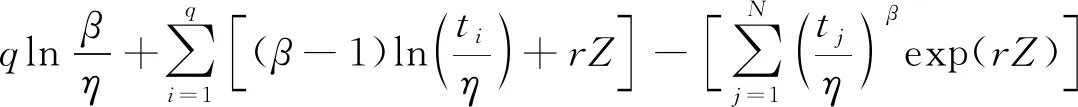
(12)

(13)

(14)

对于上述对数似然函数方程组求解方法主要有牛顿迭代法、遗传算法[17]、粒子群法。

牛顿迭代法主要是通过泰勒一阶展开，从初始值开始，分别对下一个值进行泰勒展开，不断循环，直到达到理想精度或最大迭代次数停止计算[18]，从而求得模型参数β、η、r。

原理为

f(x)=f(x0)+(x-x0)f′(x0)

(15)

步骤为

(16)

具体求解：由于上述得到了似然函数一阶方程组，所以要求得似然函数方程组的解，还需要对于其进行二次求导[19]，即

(17)

根据牛顿迭代法可得

(18)

式(18)中：β0、η0、r0为初始值。

通过牛顿迭代法求解得到3个待估参数之后，便得到了威布尔比例故障率模型以及相应的可靠度模型，继而就可以选择最小成本维修策略或者最大可用度维修策略建立决策模型，求取最优预防时间间隔。

2 综合维修优化模型

2.1 最小维修成本

针对汽车的柴油发动机，由于经济性在维修中的是首先被考虑的，其故障后维修费用远大于预防性维修费用，所以选择最小维修成本法作为决策目标，其具体模型求解如下所示。

当以单位时间内柴油发动机维修成本最小为目标，制定相应地最优维修策略。单位时间维修成本为E，其计算公式[20-22]为

(19)

式(19)中：CPM为部件的预防性维修成本；CCM为部件故障的时候维修成本；N(t)=(t/η)β为0～t内部件的平均失效数。

为了求得E的最小值，对t进行一阶求导，并等于0，得到最优预防时间间隔T为

(20)

2.2 最大可用度法

可用度A(t)表示t时刻系统处于正常状态的概率，其计算公式[23]为

(21)

(22)

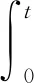
求A(t)的最大值，即转化为求t取何值时，α可以取到最小值。

2.3 综合维修优化模型

由于单方面只考虑减少柴油发动机维修成本，有可能会造成可用度无法保障，为了综合考虑柴油发动机的维修成本最小以及可用度最大，为此提出了以可用度为约束，以单位维修最少为目标，建立柴油发动机综合维修优化模型[24]，即

(23)

2.4 维修决策模型

根据综合维修优化模型得到最优预防维修时间间隔T，在故障数据中找出一组与之最接近的失效时间与伴随时间变量数据，带入威布尔比例故障率模型，得到失效率阈值下限h。在部件工作正常时，故障率低于h，即

(24)

然后根据监测的周期Δt,继续代入模型计算，得到失效率模型阈值上限h*，当设备当前状态及寿命数据代入模型后大于h*,表明设备已经处于维修区，即

(25)

将式(25)经过取对数等变形后，得到了对数风险度rZ，并将维修区域分为正常工作区、加强监测区、维修区[25-26]，即

(26)

基于综合优化维修决策流程如图1所示。

3 实例分析

3.1 模型选择

对于柴油发动机的寿命数据，它有可能服从几种分布类型，如指数分布、对数正态分布、威布尔分布等[27]。为了判断寿命数据最符合哪种分布类型，首先需要通过最大似然法估计出各种分布的参数值，然后通过拟合优度检验方法进行拟合优度检验[28]。然而，有时经过分布的拟合优度检验判断出符合条件的分布类型不止一种，所以引入了赤池信息准则(akaike information criterion，AIC)进行分布模型的最终选择[29]。AIC信息准则是基于最大熵原理，能够检验出不同模型间差异的显著性，可通过计算错判概率进行模型选择分析，其计算公式为

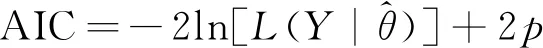
(27)

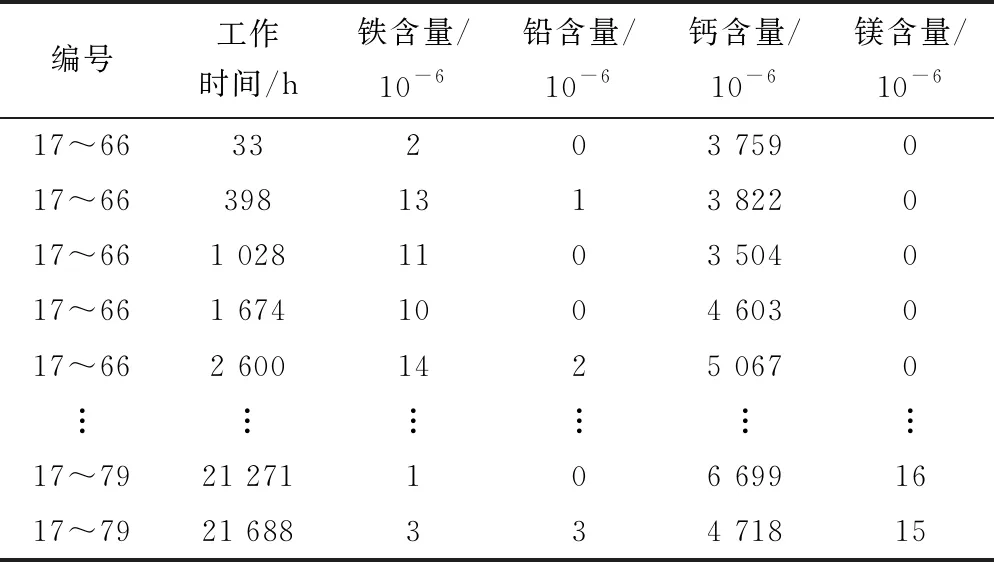
为了验证上文中选择威布尔模型的有效性，基于柴油发动机寿命数据对于对数分布、对数正态分布以及威布尔分布的AIC值进行了计算与判定。柴油发动机的故障寿命数据如表1所示。

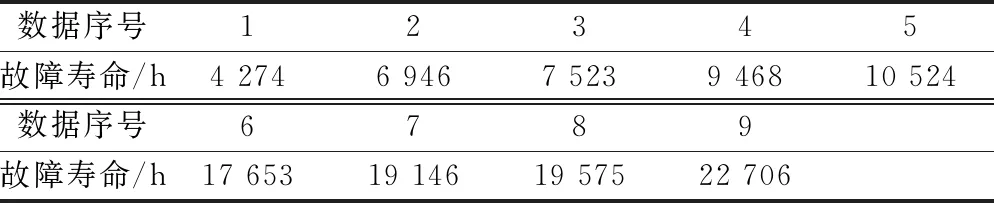
表1 故障寿命数据

首先采用极大似然估计的方法得到了3种分布的参数值，继而选择拟合优度检验方法中的K-S检验[30]对于3种分布的p值和H值进行了求解，求解结果如表2所示。

从表2可以看出，3种分布的K-S检验的H值均为0，表示接受原假设，检验结果均服从原假设分布。为了进一步确定最佳分布，下面根据AIC公式计算得到了3种分布的AIC值如意表3所示。

表2 参数估计值和K-S检验结果

表3 3种分布类型AIC值

根据AIC准则，AIC值最小的分布类型作为最佳的分布类型[31],所以推断出威布尔分布为故障数据的最佳分布类型。

3.2 模型的建立与求解

在不同阶段，柴油发动机的运行状态与柴油发动机的润滑油中的各种金属含量有着直接关系，因此本文选择其中铁、钙、镁、铅在润滑油中的含量作为模型的协变量。在监测的数据中，包括柴油发动机工作时间、换油时间、4种金属含量等数据。其部分数据如表4所示。

通过表4可以发现，在同一时刻，润滑油中4种金属含量数据量级差距较大，为了避免较大数据淹没其他数，提高模型精度，需要先将原始数据归一化。同时，为了减少协变量的个数，并得到一组更加全面的有效的特征协变量，可以对于数据进一步的处理，即通过主成分分析得到新的协变量[32-33]，在MATLAB种将主成分贡献度设置为90%，便得到了三个相互独立的新的特征协变量Z1、Z2、Z3，回归变量的相关系数矩阵和相关系数矩阵的特征值与贡献率分别如表5、表6所示。

表5 回归变量的相关系数矩阵

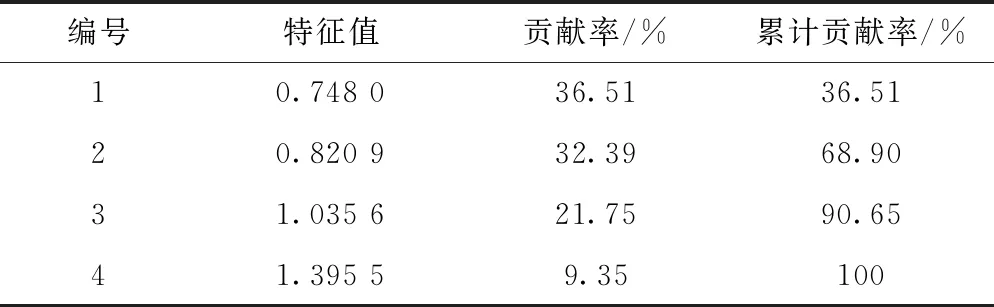
表6 相关系数矩阵的特征值与贡献率

将处理后的监测数据带入对数似然函数中，并使用牛顿迭代法借助MATLAB对于模型的3个参数进行求解，得到参数β=2.25，η=14 846，r1=-2.883，r2=0.741，r3=-1.633 ,因此威布尔比例故障率模型为

(28)

3.3 维修阈值确定

以综合维修策略作为决策方法，通过调查及历史经验，柴油发动机的预防性维修费用CPM平均为100元，故障后维修费用CCM平均为2 000元，因此CPM/CCM=0.05,将上述结果代入式(19)中，画出时间t与单位时间维修成本E的曲线如图2所示，并求出相应的最优预防时间间隔。

图2 平均时间维修成本曲线

通过图2以及相应的计算可知，当T=3 486时，单位时间维修成本可以达到最小值，并满足可用度要求，因此T=3 486为最优预防时间间隔。然后，在历史监测的寿命与油液金属含量数据中，找到一组与寿命时间最近的一组数据及其对应的3个新的协变量，将其带入WPHM模型后，可以得到相应的故障率阈值h=3.32×10-5，再将h代入式(26)中，即可得到决策阈值下限曲线为

0.741×(-0.075 2)-1.636×

(-0.083 3)]=3.32×10-5

(29)

为了进一步确定维修决策阈值上限，设置监测时间间隔时间为1 260 h，即得到时间T=4 746，同样找到一组与寿命时间最近的一组数据及其对应的3个新的协变量，代入模型后便可得到对应的故障率阈值h*=6.75×10-5，以及决策阈值上限曲线。决策阈值上下限曲线如图3所示。

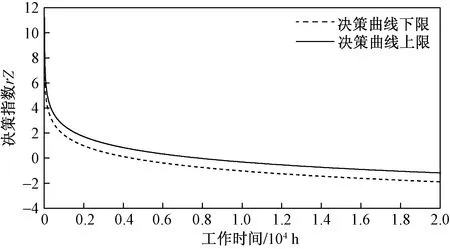
图3 决策阈值上下限曲线

在后续的维修决策中，将监测到的柴油发动机寿命时间和润滑油金属含量数据经过数据处理后，带入决策模型中，如果得到的数值处于决策曲线下方，表明工作正常，继续进行监测；如果得到的数值处于上限与下限之间，则表明需要加强监测，缩短监测的时间间隔；如果求得的数值处于决策曲线的上方，则需要对于柴油发动机采取相应的维修措施。

3.4 模型验证

为了验证上述建立的视情决策维修模型的有效性与可用性，选择监测到的一组同类型的柴油发动机的润滑油中金属含量数据以及对应的运行状况进行了分析验证。该发动机从1994年1月开始运行，在运行到1994年12月出现了故障，总共运行了7 523 h。将柴油发动机的金属含量数据经过PCA后，带入维修决策模型，得到相应的对数风险值并在图中画出，如图4所示。

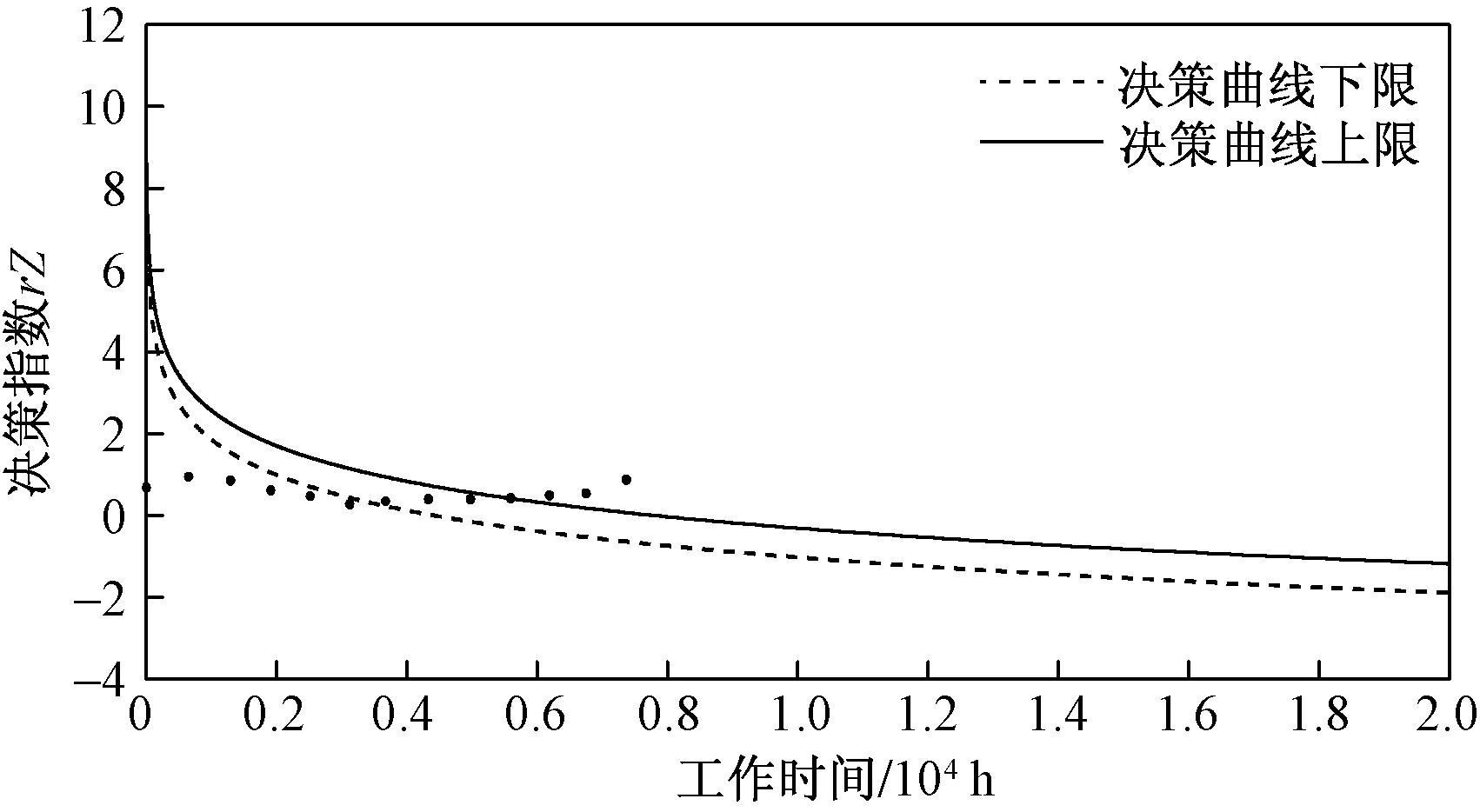
图4 柴油发动机状态维修曲线图

从图4可以看出，该柴油发动机在运行到2 516 h的时候，其最接近决策曲线下限，这时需要加强监测；在运行6 196 h后，其状态接近决策曲线上限，此时应当采取一定的预防性维修措施。根据该发动机的实际状态，由于没有采取相应的维修措施，其在运行到7 523 h发生了故障，该实验结果表明本文提出的决策方法有效合理，可用于实际的该型发动机视情维修决策。

4 结论

基于收集的柴油发动机寿命数据及其对应的润滑油金属含量数据，在对其进行PCA后，选取了累计贡献率达到90%的3个特征协变量，使用最大似然估计的方法估计得到了威布尔比例危险率模型参数，建立了威布尔比例故障率模型；进而以最小维修成本为目标，以最大可用度作为约束，计算求得了最优预防时间间隔，建立了同类型柴油发动机维修决策模型，为后续的状态维修提供了有效的决策方法，不仅最大可能地降低了维修成本，又保证了柴油发动机的安全运行和最大可用时间。最后以同类型发动机的状态及寿命数据为例，验证了该模型可以有效地通过寿命和金属含量数据判断柴油发动机是否需要进行维修，具有较大的应用于视情维修决策的实用价值。