基于边界打靶法的横向流作用下悬臂梁静态模态函数求解

王小文 周益娴

摘  要：该文以横向流作用下的单根悬臂梁结构为对象，研究其静态偏折模态形状函数，为后续反应堆内设备一阶梁式振型下附加质量的求解打下基础。首先，采用大挠度非线性方程组进行建模;其次，采用一种边界打靶法来进行上述非线性微分控制方程求解，得到悬臂梁的偏折曲线的数值解，并将数值计算结果和存在解析解的情况下的解析结果进行对比。

关键词：筒仓卸载悬臂梁   静态偏折模态形状函数   边界打靶法   梁式振型函数

中图分类号：TU311                         文献标识码：A文章编号：1672-3791（2021）08（b）-0004-04

Solution of Static Deflection Mode Shape Function of Cantilever Beam under Transverse Flow Based on Boundary Shooting Method

WANG Xiaowen   ZHOU Yixian*

（Beijing Key Laboratory of Passive Nuclear Safety Technology， North China Electric Power University， Beijing， 102206 China）

Abstract： In this paper， it studies the cantilever beam structure under the action of transverse flow， and focus on the derivation of its static cantilever deflection mode shape function， in order to lay foundation for the calculation of hydrodynamic added mass for the beam mode vibration of nuclear reactor internal cantilever components. Firstly， a set of nonlinear differential equations for the analysis of the single cantilever beam has been proposed. Secondly， to solve the nonlinear differential equations， we used a boundary shooting framework. The results of the numerical simulation agree well with the analytical solution.

Key Words： Cantilever beam; Static deflection mode shape; Boundary shooting method; Beam mode function

反應性事故发生后，堆内构件在流体中的振动在反应堆安全问题中至关重要。堆内构件和高能流的接触引发设备的振动，进而使得   浸没于流动流体中的设备，如设备支承筒、燃料棒或热交换器管等发生疲劳，导致破损。随着反应堆规模的扩大，堆内构件更易弯曲，堆内冷却剂流量增加，流致振动问题愈发严重。流致振动问题从1950年便开始进行研究，但由于该问题涉及流固耦合和非线性科学，因此理论研究难度很大。目前，研究对象大多为不同堆型的燃料组件，其边界条件一般为两端固定，而对设备支承筒等悬臂结构研究较少。且主要为实验和模拟研究，理论研究工作较少。实验和模拟方法主要针对特定的工程工况，所得结果精确，但耗时较长。工程实践中前期设计阶段往往需要理论推导结果加以指导。

1  理论分析

根据核电站内构件的工程特点，部分结构可简化为横向流作用下悬臂梁结构振动问题[1-2]，由于高径比较大，其一阶梁式振型较易被激励，有必要对一阶梁式振型模态进行单独研究，且堆内设备一阶梁式振型下的附加质量和频率的求解需要知道其静态偏折模态形状函数，堆内构件一般可简化为具有一定刚度和弹性的梁[3-5]。因此，该文将以单根悬臂弹性梁结构为研究对象，求解其偏折模态形状函数。

考虑底端固定的悬臂梁，其他位置无任何支撑，并且有分布载荷作用于其上，悬臂梁的截面几何形状影响其刚度和弯曲机理[6-7]，我们假设其横截面在垂直方向上不发生变化，最大弯矩和剪切应力应该位于悬臂梁的底部。假设只有一根悬臂梁完全暴露在水流中，而周围没有其他悬臂梁来改变垂直速度分布，悬臂梁受水流的拉力大小为：

式中，FD为流体对悬臂梁浸没部分的拉力，CD为拉力系数，ρ为水的密度，u（z）为垂直方向的速度分布，A为物体浸入部分垂直于水流平面的投影面积。根据欧拉伯努利方程，该悬臂梁弯曲的微分控制方程如下：

（2）

（3）

（4）

式中，;;;。θ为偏折角度，s表示沿曲线的距离，M表示一个截面所受弯曲力矩，I表示惯性矩，E表示弹性模量，V表示作用在梁截面上的剪切应力，w（z）表示水流对梁产生的分布载荷，x和z分别表示梁任意截面与其底部的水平距离和垂直距离。

公式（2）至公式（4） 控制悬臂梁弯折的角度，由于悬臂梁底端固定，因此有：

sinθ（z*=0）=0（5）

根據工程特点，考虑悬臂梁顶端不浸没于水中的情况，因此露出水面位置悬臂梁所受弯矩和剪力为0，得到边界条件：

M*（z*=1）=0（6）

V*（z*=1）=0（7）

2  方法介绍

为了更好地利用边界打靶法去求解上述的微分方程，我们引入了3个变量x1，x2，x3：

（8）

式（2）至式（4）改写为：

（9）

3个边界条件为：

（10）

边界打靶法是利用初值条件去代替已知边界条件进行求解，通过不断改变初始值让其逐渐逼近给定的边界条件，因此调整边界的公式选取十分重要，我们设定了两个不断调整初始条件的关系式公式（11）和公式（12）：

（11）

（12）

其中b2和b3分别代表代表顶端z*=1处x2和x3的边界条件，α代表打靶系数，其值小于1，该值的选取取决于作用在悬臂梁的载荷大小。i表示的是迭代的步数。

3  结果与分析

验证计算程序，我们采用Li等人[6]提供的数值进行计算，并将结果与解析解进行对比。悬臂梁和流场的参数为：抗弯刚度EI=2.5×10-7，悬臂梁尺寸D=2.4×10-5 m，水深h=0.05 m，水密度ρ=1×103 kg/m3，水流的平均速度，拉力系数CD=1.2。流场的分布满足指数分布：

其中m=3.156，求解式（2）～（4）可以获得沿悬臂梁的偏折角度、弯矩以及剪切力等分布情况。其解析解表达如下：

（14）

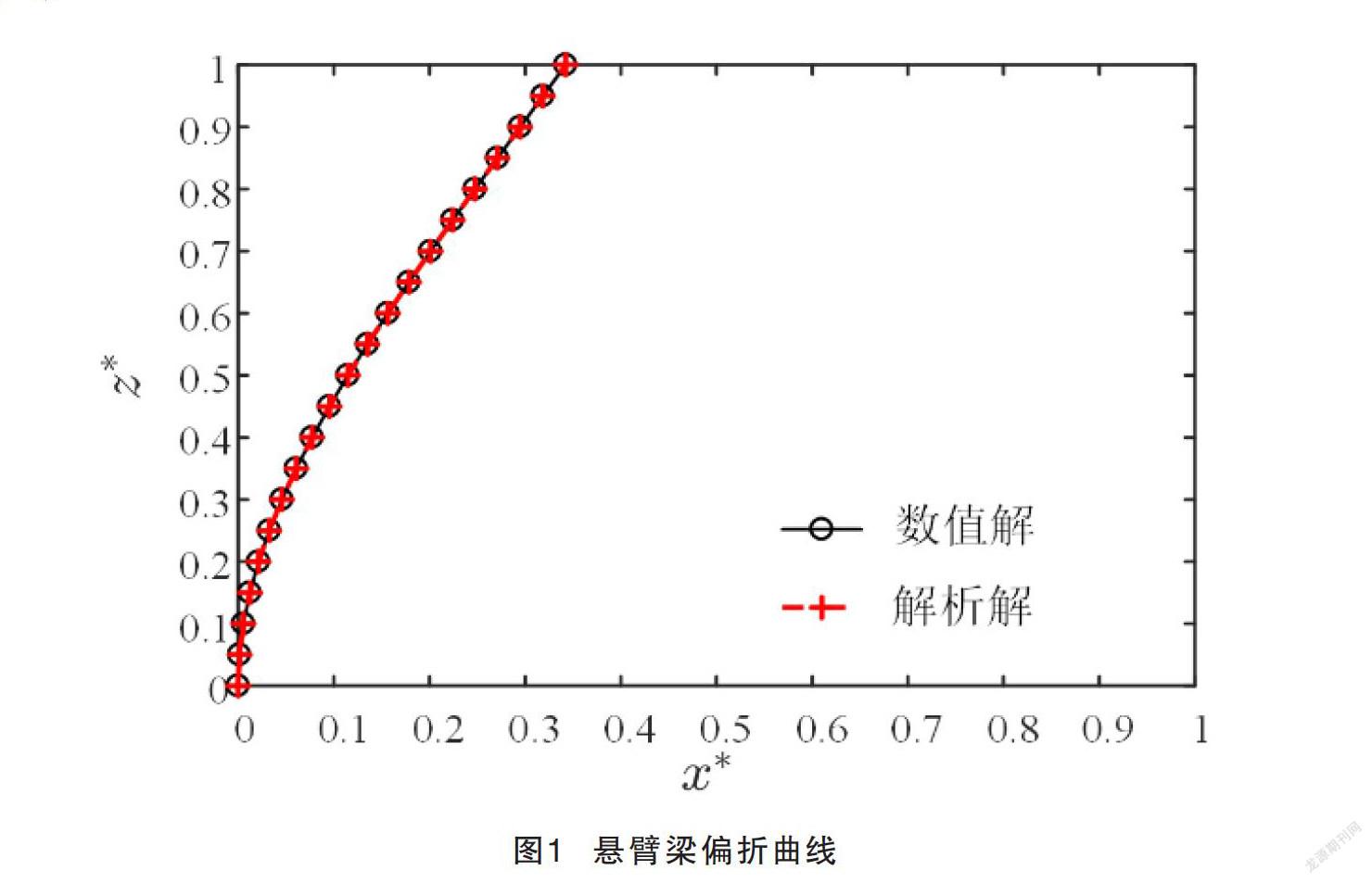
图1给出了在指数分布流场中，悬臂梁的偏折曲线的数值解及解析解对比图。可以看到数值解和解析解吻合较好，图中最大相对误差为3.02×10-6，可见计算精度很高，计算程序得到了验证。

接下来该文研究不同参数对悬臂梁弯折情况的影响。图2（a）展示了不同抗弯刚度EI的悬臂梁的偏折情况，当抗弯刚度大于5×10-7 N m2时，悬臂梁偏折很小或基本没有偏折。而刚度较小时可产生较大的偏折。图2（b）展示了不同来流平均速度u的悬臂梁的偏折情况。当平均速度小于0.25 m/s时，悬臂梁偏折很小或基本没有偏折，而速度较大时可产生较大的偏折。

4  结语

该文以横向流作用下的悬臂梁结构为研究对象，采用理论分析和数值计算相结合方法，研究其偏折模态形状函数。根据反应堆内组件的结构特点，采用大挠度非线性方程组来进行建模，论证了该模型处理悬臂梁偏折问题的适用性。为求解该问题，使用一种边界打靶法来进行上述非线性微分控制方程的求解，得到悬臂梁的偏折曲线的数值解，并将数值计算和解析解结果对比，二者吻合度极高，计算程序得到验证。后续的工作将深入研究迭代次数和打靶系数对结果的影响。

参考文献

[1] FERRARI G，FRANCHINI G， BALASUBRAMANIAN P， et al.Nonlinear Vibrations of a Nuclear Fuel Rod Supported by Spacer Grids[J].Nuclear Engineering and Design，2020（361）：110503.

[2] GINEAU A，LONGATTE E，LUCOR D，et al.Macroscopic Model of Fluid Structure Interaction in Cylinder Arrangement using Theory of Mixture[J].Computers & Fluids，2020（202）：104499.

[3] DE SANTIS D，SHAMS A.Numerical Modeling of Flow Induced Vibration of Nuclear Fuel Rods[J].Nuclear Engineering and Design，2017（320）：44-56.

[4] DE SANTIS D，KOTTAPALLI S，SHAMS A.Numerical Simulations of Rod Assembly Vibration Induced by Turbulent Axial Flows[J].Nuclear Engineering and Design，2018（355）：94-105.

[5] DE SANTIS D，SHAMS A.An Advanced Numerical Framework for the Simulation of Flow Induced Vibration for Nuclear Applications[J].Annals of Nuclear Energy，2019（130）：218-231.

[6] LI C W， XIE J F.Numerical Modeling of Free Surface Flow over Submerged and Highly Flexible Vegetation[J].Advances in Water Resources，2011，34（4）：468-477.

[7] JING H F，CAI Y J，WANG W H，et al.Investigation of Open Channel Flow with Unsubmerged Rigid Vegetation by the Lattice Boltzmann Method[J].Journal of Hydrodynamics，2020（32）：771-783.