诊断试验样本量估计及其在nQuery和SAS软件上的实现*

南方医科大学公共卫生学院生物统计学系(510515) 吴研鹏 钱晨坚 陈平雁 段重阳

1.单样本灵敏度/特异度的检验

方法：Li和Fine(2004)[1]提出了筛检试验基于单样本灵敏度/特异度检验的样本量估计方法，其检验效能基于二项分布的确切概率法，采用两步迭代计算。以灵敏度为例计算公式如下：

第一步：

(1)

(2)

第二步：

(3)

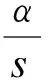
将公式(1)至(3)中的Se0和Se1分别替换为1-Sp0和1-Sp1，N+替换为N-，就是特异度的单样本样本量估计公式，其中，Sp0和Sp1分别为原假设和备择假设下的特异度，N-为阴性组样本量，最终总样本量为n=N-/(1-p)。

需要特别指出，上述公式用于全人群筛检时p是人群患病率，如果用于医院就诊人群的诊断，p应该代表就诊人群的阳性病例的比例，即试验样本是随机就诊人群而不是选择人群，否则所估计的样本量会偏高或偏低，其中若选择人群p偏高，则所估计样本量偏高，反之偏低[2-4]。

【例1】 某研究旨在评价高危型人乳头瘤病毒(HR-HPV-DNA)检测较超薄液基细胞学(TCT)检测在宫颈癌筛查中的诊断价值，筛查对象为35～64岁已婚妇女，以病理活检结果为金标准。根据既往研究结果，该人群的宫颈癌患病率为3.32/万。预期HR-HPV-DNA检测的灵敏度为0.850，以既往研究报告TCT诊断宫颈癌的灵敏度0.765为目标值(即原假设Se0=0.765)。设定单侧检验水准α=0.025，检验效能为80%，试估计HR-HPV-DNA检测技术的灵敏度不低于0.765所需样本量。

nQuery Advanced 8.6.0.0实现：设置单侧检验水准α=0.025，检验效能1-β=80%，其他数据相应代入，在nQuery Advanced 8.6.0.0 主菜单选择：

方法框中选择：One Sensitivity

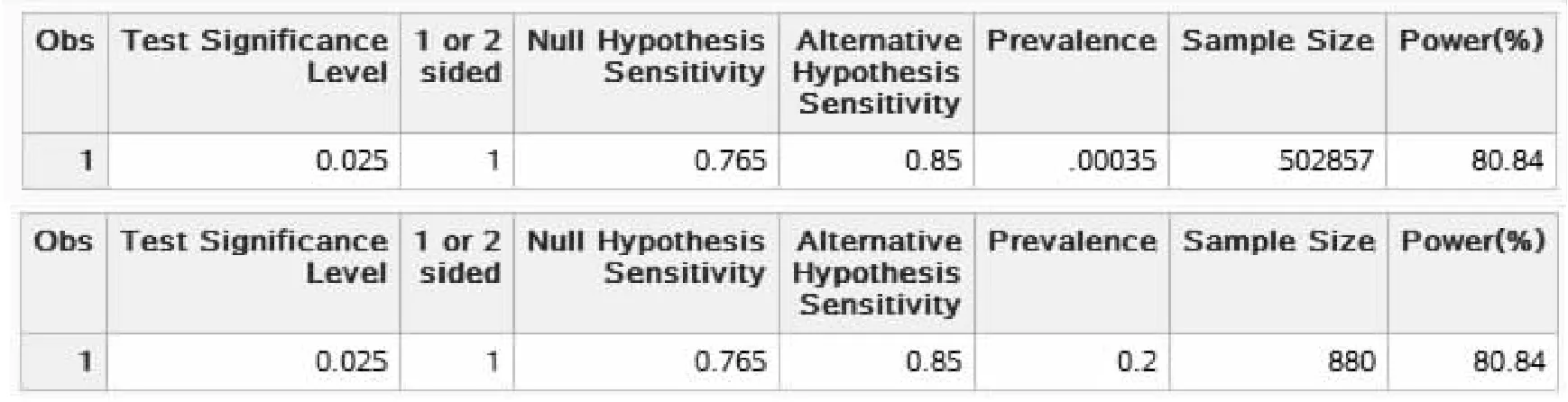
在弹出的样本量计算窗口将各参数值键入，如图1第1列数据所示，结果为n=502857，即本试验的最少样本量为502857例。

若该检测方法应用于医院内就诊人群，且假设医院既往接受该检测方法的患者中病例活检阳性的比例为20%，如图1第2列所示，则HR-HPV-DNA检测技术不低于0.765所需样本量为880例。由此可见，基于筛查和诊断的目的不同，样本量有很大差别，能否准确估计样本量，关键之一在于筛查人群患病率或就诊人群阳性率的正确估计。

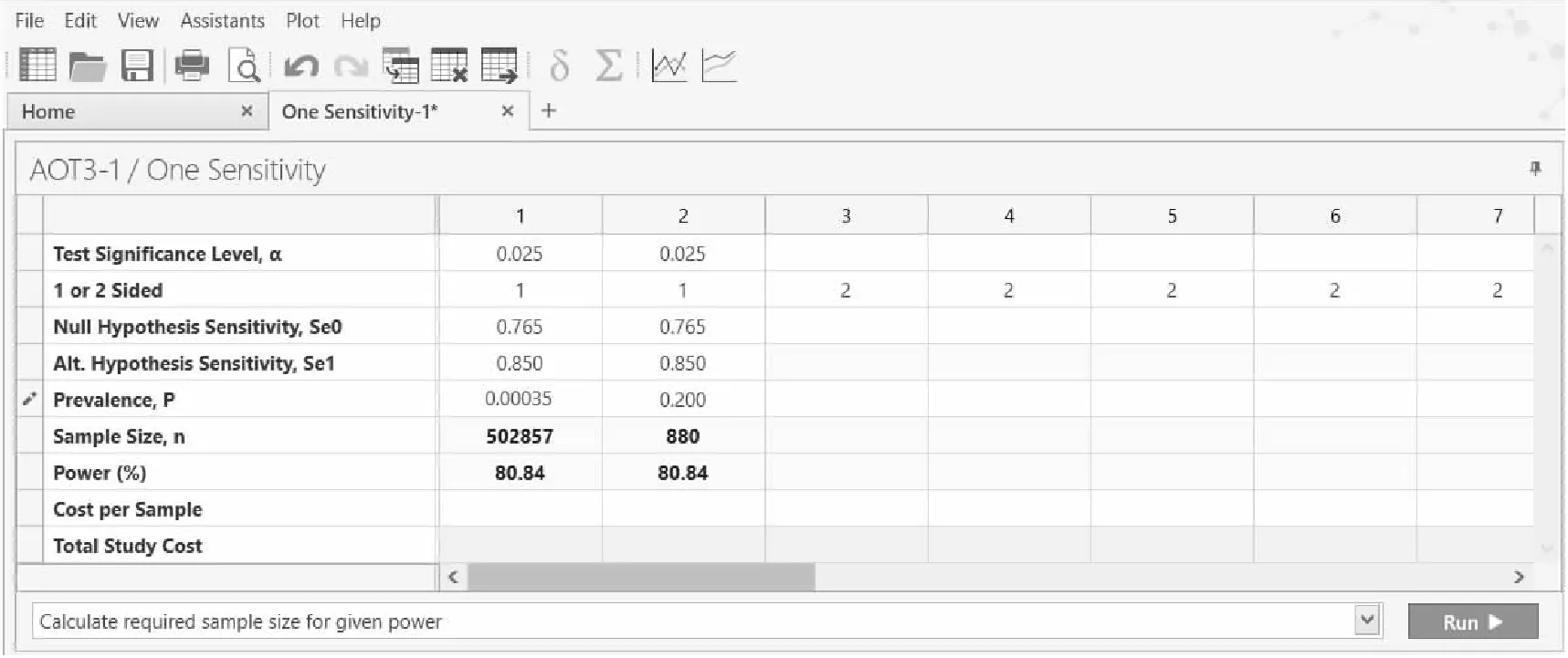
图1 nQuery Advanced 8.6.0.0 关于例1样本量估计的参数设置与计算结果

SAS 9.4软件实现：

%macro sensitivity(alpha= /* 检验水准 */

，side= /* 单双侧检验，1表示单侧检验，2表示双侧检验 */

，se0= /* 原假设下的灵敏度，即

灵敏度目标值 */

，se1= /* 备择假设下的灵敏度，即预期的检验灵敏度 */

，p= /* 阳性率(人群患病率)*/

，power=/* 检验效能 */

)；

/*判断输入的参数是否符合要求，并输出日志提示 */

%if(&alpha>1 or &alpha<0)%then %do；

%put ERR%STR(OR)：Test significance level must be in 0-1；

%goto exit；

%end；

%if(&side^=1 and &side^=2)%then %do；

%put ERR%STR(OR)：s=1 or 2；

%goto exit；

%end；

%if(&p>1 or & p<0)% then %do；

%put ERR%STR(OR)：Overall Event Rate(P)must be in 0-1；

%goto exit；

%end；

%if(&power>100 or & power<0)% then %do；

%put ERR%STR(OR)：Power must be in 0-100；

%goto exit；

%end；

/*定义函数ca，用于计算原假设下X分布的上、下α布的分位数 */

proc datasets nolist nodetails NoWarn lib=work；

delete funcsol/memtype=data；

quit；

proc fcmp outlib=work.funcsol.conversion；

function ca(q，n，s)；

n1=1；

x=0；

%**从阳性样本量初始值1开始迭代 *；

do until(x gt q)；

x=cdf('binomial'，n1，s，n)；

n1=n1+1；

end；

n1=n1-1；

return(n1)；

endsub；

run；

options cmplib=(work.funcsol)；

/*样本量估计 */

data a；

%**参数输入 *；

side=&side；

se0=&se0；

se1=&se1；

alpha=&alpha；

p=&p；

power1=&power；

%**两步迭代计算样本量

第一步：调用函数ca，迭代计算原假设下X分布的上、下α布的分位数

第二步：不断增加阳性样本量，迭代计算检验效能，直至满足设定条件*；

n1=2；

power=0；

do until(power>=&power)；

x1=ca(1-alpha/side，n1，se0)；

x2=ca(alpha/side，n1，se0)；

if side=2 then power=(1-probbnml(se1，n1，x1)+probbnml(se1，n1，x2-1))*100；

if side=1 then do；

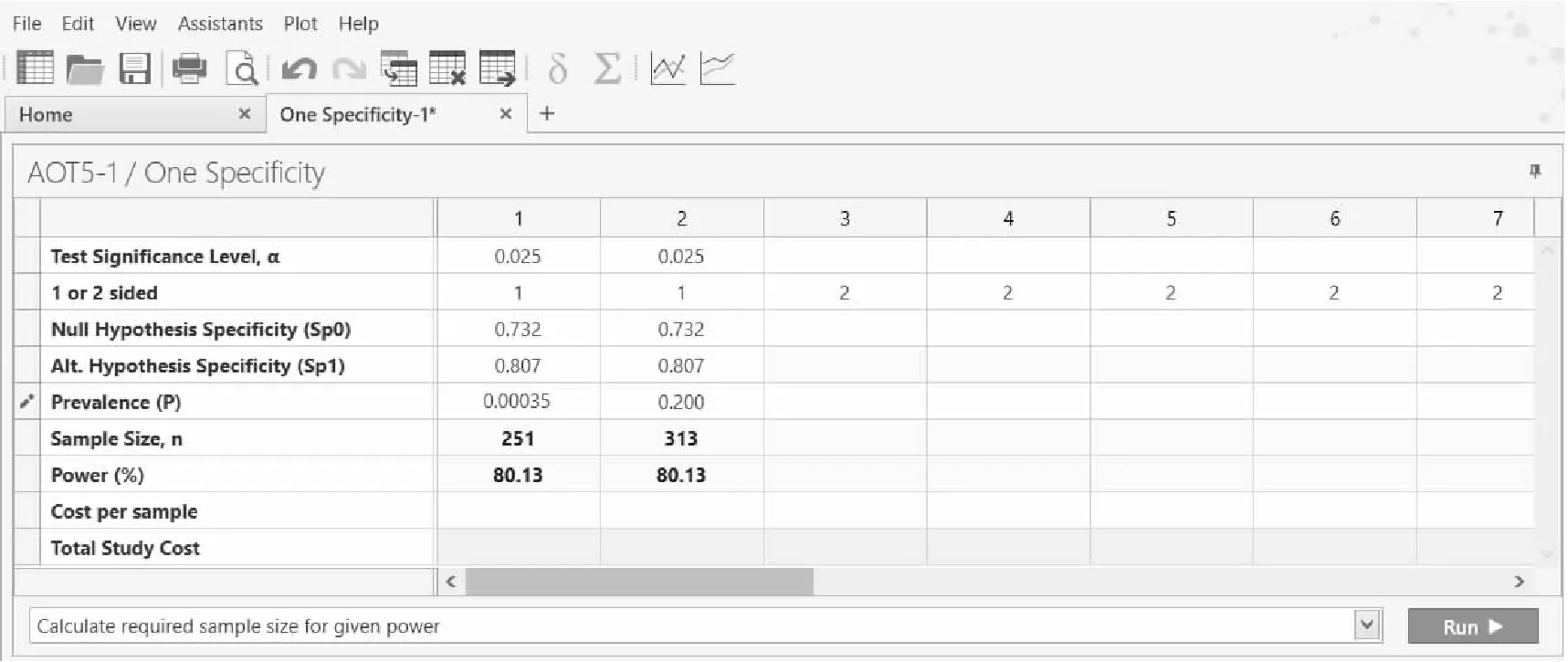
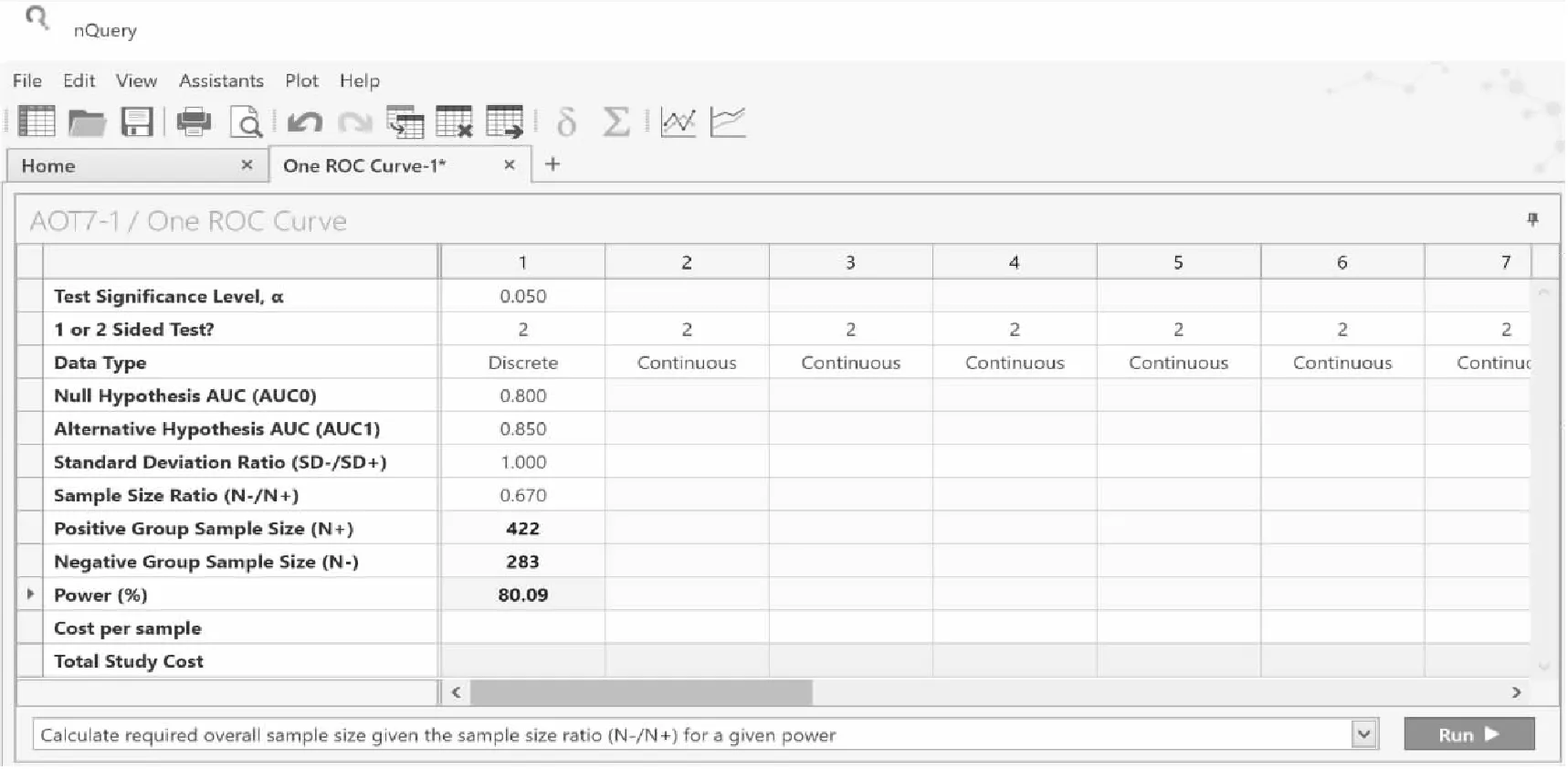
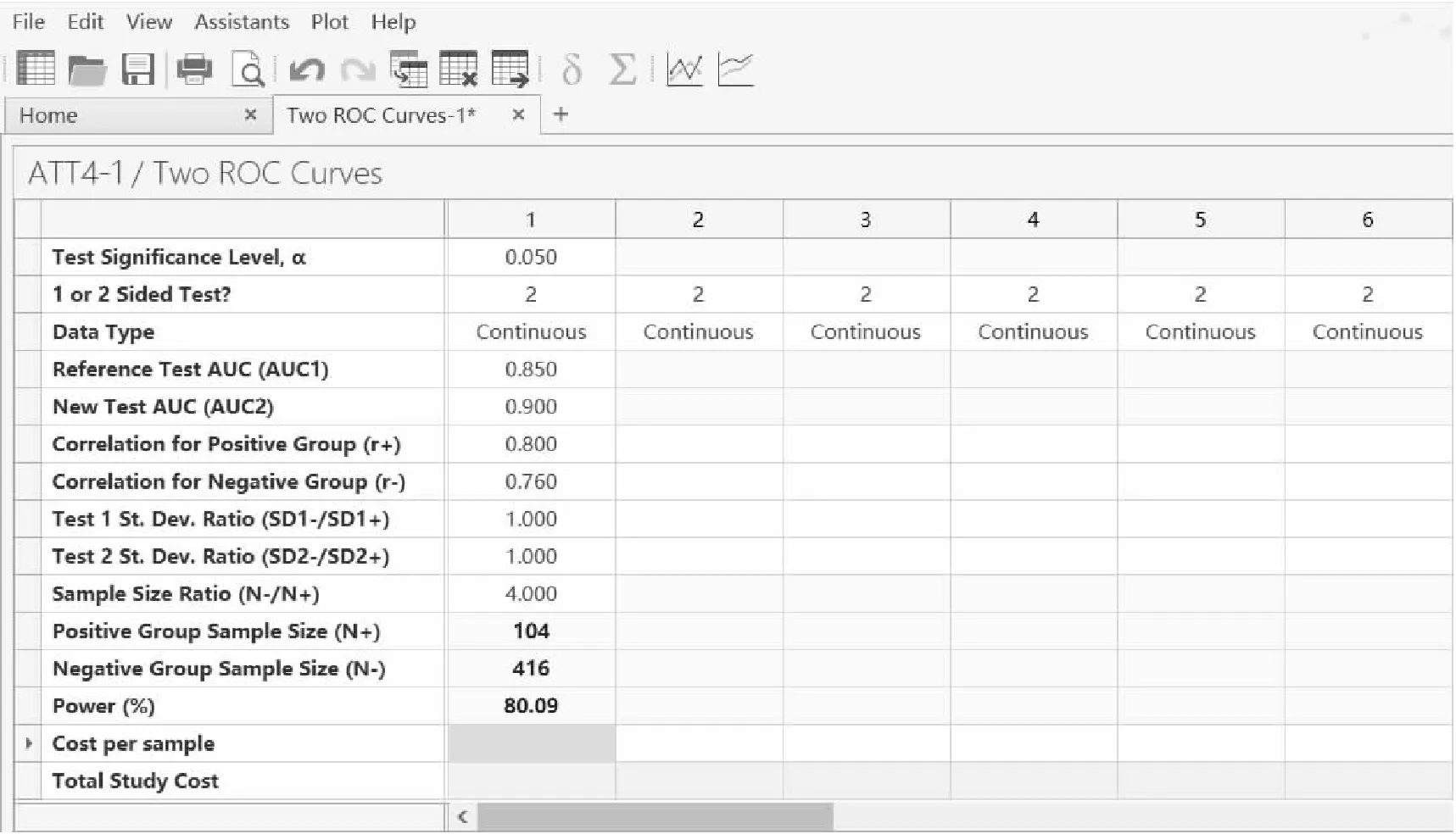
if se0

else power=(probbnml(se1，n1，x2-1))*100；

end；

n1=n1+1；

end；

n1=n1-1；

power=round(power，0.01)；

n=floor(n1/p)；%**计算最终总样本量*；

run；

/*结果输出 */

proc print data=a label；

var alpha side se0 se1 p n power；

label alpha="Test Significance Level"

side="1 or 2 sided"

se0="Null Hypothesis Sensitivity"

se1="Alternative Hypothesis Sensitivity"

p='Prevalence'

n="Sample Size"

power="Power(%)"；

quit；

%exit：

%mend sensitivity；

%sensitivity(alpha=0.025，side=1，se0=0.765，se1=0.850，p=0.00035，power=80)

%sensitivity(alpha=0.025，side=1，se0=0.765，se1=0.850，p=0.20，power=80)

SAS运行结果：

图2 SAS 9.4 关于例1样本量估计的参数设置和计算结果

【例2】以例1为例，预期HR-HPV-DNA合并TCT检测法诊断的特异度为0.807，以既往研究报告TCT诊断宫颈癌的特异度0.732为目标值(即原假设Sp0=0.732)，设定单侧检验水准α=0.025，检验效能为80%下，试估计HR-HPV-DNA合并TCT检测技术的特异度不低于0.732所需样本量。

nQuery Advanced 8.6.0.0实现：设置单侧检验水准α=0.025，检验效能1-β=80%，其他数据相应代入，在nQuery Advanced 8.6.0.0主菜单选择：

方法框中选择：One Specificity

弹出的样本量计算窗口将各参数值键入，如图3第1列数据所示，结果为n=251。即本试验的最少样本量为251例。另外，考虑该检测技术在医院就诊人群的应用，且假设医院既往接受该检测方法的患者中病例活检阳性的比例为20%，如图3第2列数据所示，则HR-HPV-DNA检测技术特异度不低于0.732所需样本量为313例。

图3 nQuery Advanced 8.6.0.0关于例2样本量估计的参数设置与计算结果

SAS软件实现：

在单样本灵敏度的SAS样本量估算程序中，将输入参数Se0和Se1直接替换为Sp0和Sp1，迭代公式中，Se0和Se1分别替换为1-Sp0和1-Sp1，最后计算出总样量n=N-/(1-p)。

SAS运行结果：

图4 SAS 9.4 关于例2样本量估计的参数设置和结果

2.单样本AUC检验

方法：Obuchowski和McClish[5]以及Hanley和McNeil[6-7]给出了观测变量为等级类型和连续类型下的单样本AUC(ROC曲线下的面积)检验的样本量和检验效能的估计方法，其计算公式如下：

(4)

(5)

等级变量类型的资料常见于放射学研究，例如用CT扫描识别组织病变，观测变量记录为“正常”，“可能正常”，“不确定”，“可能不正常”，“不正常”。Obuchowski和McClish给出了等级变量下V(θ)估计公式：

(6)

(7)

(8)

式中，θ表示AUC；f和g分别表示由A和B构成的函数式。A和B构造基于如下双正态法：

(9)

(10)

等级型观测变量下，B值一般无法直接得到，可通过与观测变量密切相关的连续测量指标，间接估计阴性组和阳性组中对应的潜在连续型观测的标准差比值，也可直接根据两组观测的离散程度估计其比值；不确定情况下，通常设B为1，得到样本量的保守估计[5]。

连续型观测变量下，可基于AUC值直接估计方差，Hanley和McNeil给出了连续型变量下的V(θ)估计公式：

(11)

样本量计算中，根据不同观测数据类型，直接将θ=θ0和θ=θ1带入相应V(θ)计算公式中即可得到V(θ0)与V(θ1)的估计值。

【例3】 某研究欲评估磁共振成像(MRI)在诊断疑似膝关节损伤患者是否发生关节软骨损伤的临床价值，关节镜检查作为金标准，影像科医生根据每个病人MRI显像做如下评分：1=肯定没有软骨异常；2=可能没有软骨异常；3=怀疑软骨异常；4=可能有软骨异常；5=肯定软骨异常。研究显示疑似膝关节损伤患者中60%存在软骨异常，因此正常组与异常组样本量比值设为0.67(即0.4/0.6)，假设正常组和异常组的观测标准差相同，即B=1。预期MRI诊断AUC为0.850，AUC的目标值为0.80，设定双侧检验水准α=0.05，检验效能为80%，试估计MRI诊断的AUC高于目标值所需样本量。

nQuery Advanced 8.6.0.0实现：设置双侧检验水准α=0.05(相当于单侧0.025)，检验效能1-β=80%，其他数据相应代入，在nQuery Advanced 8.6.0.0主菜单选择：

方法框中选择：One Roc Curve

在弹出的样本量计算窗口将各参数值键入，如图5所示，结果为422和283，即本试验所需样本量为阳性组422例和阴性组283例，共需705例。

图5 nQuery Advanced 8.6.0.0关于例3样本量估计的参数设置与计算结果

SAS 9.4软件实现：

%macro oneroc(

alpha=/* 检验水准*/

，side=/* 单双侧检验，1表示单侧检验，2表示双侧检验 */

，type=/* 观测变量数据类型，1表示等级变量类型，2表示连续变量类型 */

，theta0=/* 原假设下AUC，即AUC目标值 */

，theta1=/* 备择假设下AUC，即预期AUC */

，B=/* 等级变量类型中，阴性组和阳性组潜在连续观测的标准差比值*/

，R=/* 总样本量中阴性与阳性例数的比值*/

，power=/* 检验效能*/

)；

/* 判断输入的参数是否符合要求，并输出日志提示*/

%if(&alpha>1 or &alpha<0)%then%do；

%put ERR%STR(OR)：Test significance level must be in 0-1；

%goto exit；

%end；

%if(&side^=1 and &side^=2)%then%do；

%put ERR%STR(OR)：s=1 or 2；

%goto exit；

%end；

%if(&type^=1 and &type^=2)%then%do；

%put ERR%STR(OR)：type=1 or 2；

%goto exit；

%end；

%if(&power>100 or &power<0)%then%do；

%put ERR%STR(OR)：Power must be in 0-100；

%goto exit；

%end；

/* 定义函数V，用于计算原假设和备择假设下的AUC方差*/

proc datasets nolist nodetails NoWarn lib=work；

delete funcsol/memtype=data；

quit；

proc fcmp outlib=work.funcsol.conversion；

function V(theta，B，R，type)；

pi=constant(′pi′)；

if type=2 then do；

v=theta/(R*(2-theta))+2*theta*theta/(1+theta)-theta*theta*(1+R)/R；

end；

if type=1 then do；

A=PROBIT(theta)*sqrt(1+B**2)；

E=exp(-A*A/(2+2*B**2))；

g=A*B*E/(sqrt(2*pi*((1+B**2)**3)))；

f=E/sqrt(2*pi*(1+B**2))；

v=f**2*(1+B**2/R+A**2/2)+g**2*(B**2)*(1+R)/(2*R)；

end；

return(v)；

endsub；

run；

options cmplib=(work.funcsol)；

/* 样本量估计 */

data oneroc；

%**参数输入 *；

theta0=&theta0；

theta1=&theta1；

side=&side；

alpha=&alpha；

B=&B；

R=&R；

type=&type；

power=&power；

%**样本量计算 *；

N_p1=(probit(1-alpha/side)*(sqrt(V(theta0，B，R，type)))+probit(power/100)*(sqrt(V(theta1，B，R，type))))**2/((theta1-theta0)**2)；

N_p=ceil(N_p1)；

N_n=N_p*R；

N_n=ceil(N_n)；

power=probnorm((sqrt(N_p)*ABS(theta1-theta0)-probit(1-alpha/side)*

sqrt(V(theta0，B，R，type)))/sqrt(V(theta1，B，R，type)))*100；power=round(power，0.01)；

run；

data oneroc1；

set oneroc；

if type=2 then q=′Continuous′；

if type=1 then q=′Discrete′；

run；

/* 结果输出 */

proc print data=oneroc1 label；

var alpha side q theta0 theta1 B R N_p N_n power；

label alpha=“Test significance level”

side=“1 or 2 sided test”

q=“Data Type”

theta0=“Null Hypothesis AUC”

theta1=“Alternative Hypothesis AUC”

B=“Standard Deviation Ratio”

R=“Sample Size Ratio”

N_p=“Positive Group Sample Size”

N_n=“Negative Group Sample Size”

power=“Power(%)”；

quit；

%exit：

%mend oneroc；

%oneroc(alpha=0.05，side=2，type=1，theta0=0.800，theta1=0.850，B=1，R=0.67，power=80)

SAS运行结果：

图6 SAS 9.4 关于例3样本量估计的参数设置与计算结果

3.配对样本AUC检验

方法：与单样本AUC检验不同，将目标AUC值θ0替代成同人群下的另一种诊断AUC值θ2，即进行配对样本AUC检验，其样本量和检验效能的估计方法与单样本AUC检验同时提出[5，7]，其计算公式如下：

(12)

(13)

式中，Δ表示两组诊断下的AUC差值，即θ2-θ1；V0(Δ)和V1(Δ)分别表示Δ在原假设和备择假设下的方差函数，其计算公式如下：

V0(Δ)=2V(θ1)-2C(θ1，θ1)

(14)

V1(Δ)=V(θ1)+V(θ2)-2C(θ1，θ2)

(15)

V(θi)的意义和计算方法同上述单样本AUC检验，计算方法见公式(6)至(11)。C(θi，θj)表示θi和θj协方差或近似协方差，其计算方法也取决于观测变量是等级型还是连续型。

对于等级变量，C(θi，θj)的估计公式：

(16)

式中，r-和r+分别表示双正态法下(见公式(9))，阴性组中两诊断观测的相关系数和阳性组中两诊断观测的相关系数，等级型观测下通常不能直接得出，计算样本量时可参考两组等级观测间秩相关系数，考虑一系列合理取值。下标i，j标注的参数分别是诊断试验i，j中对应的参数，上述公式中其余参数意义和计算方法与在单样本AUC检验中一致，这里不再赘述。

对于连续型变量，Hanley和McNeil给出了V(θi)(见公式(11))和C(θi，θj)的估计公式：

(17)

式中r表示θ1和θ2的相关系数，利用查表法，根据r+和r-的平均值及θ1和θ2平均值，可在 Hanley和McNeil提供的表中查到对应r值，不在表中的值可通过一定合理外推得出[7](r值表见附录表1)。与等级类型中的双正态法估计方法不同，这里r+和r-可基于阳性组和阴性组中的连续观测，使用Pearson相关系数或秩相关系数直接估计得出。

表1 r值表*

【例4】某研究欲比较血氧饱和度下降指数(ODI)和呼吸紊乱指数(RDI)对是否患阻塞性睡眠呼吸暂停综合征(OSA)的诊断价值。对同一组病人的OSA诊断预试验中，ODI指数诊断法的AUC为0.85，RDI指数诊断法的AUC为0.90；两诊断指数在OSA阳性组中的相关系数r+为0.80，阴性组中的相关系数r-为0.76；两诊断指数的阴性组与阳性组标准差比值B1和B2分别为1。试估计双侧检验水准α=0.05，检验效能为80%，阴性组和阳性组的样本比例R=4，能够发现两种指数诊断的AUC差异所需的样本量。

nQuery Advanced 8.6.0.0实现：设置检验水准α=0.05，双侧检验，检验效能1-β=80%，其他数据相应带入。在nQuery Advanced 8.6.0.0主菜单选择：

方法框中选择：Two Roc Curve

在弹出的样本量计算窗口将各参数值键入，如图7所示，结果为104和416。即本试验所需样本量为阳性组104例，阴性组416例，共需520例。

图7 nQuery Advanced 8.6.0.0 关于例4 样本量估计的参数设置与计算结果

SAS 9.4软件实现：

%macrotworoc(

alpha= /*Test significance level*/

，side= /*1：one sided test，2：two sided test*/

，type= /*1：Discrete，2：Continuous*/

，theta1= /*Reference Test AUC*/

，theta2= /*New Test AUC*/

，r1= /*Correlation for Positive Group*/

，r2= /*Correlation for Negative Group*/

，B1= /*Test 1 St.Dev.Ratio*/

，B2= /*Test 2 St.Dev.Ratio*/

，R= /*Sample Size Ratio*/

，power=/*Power(%)*/

，rvalue=/*根据r+和r-的平均值、AUC的平均值查表进行赋值，不能为空。比如此例为0.72*/

)；

%let error=；

/*判断输入的参数是否符合要求，并输出日志提示 */

%if %length(&rvalue.)=0 %then %do；

%let error=1；

%put ERROR：宏参数(rvalue)不能为空。；

%end；

%if(&alpha.>1 | &alpha.<0)%then %do；

%let error=1；

%put %str(ERROR：Test significance level%'s range：0-1)；

%end；

%if(&side.^=1 & &side.^=2)%then %do；

%let error=1；

%put %str(ERROR：Side%'s range：1 OR 2)；

%end；

%if(&type.^=1 & &type.^=2)%then %do；

%let error=1；

%put %str(ERROR：type%'s range：1 OR 2)；

%end；

%if(%sysevalf(&theta1.+&theta2.)<1.4 | %sysevalf(&theta1.+&theta2.)>1.95)%then %do；

%let error=1；

%put %str(ERROR：sum%(theta1，theta2%)%'s range：1.4<=P=<1.95)；

%end；

%*r取值范围超过r值表；

%if(%sysevalf(&r1.+&r2.)<0.04 | %sysevalf(&r1.+&r2.)>1.8)%then %do；

%let error=1；

%put %str(ERROR：sum(r1，r2)%'s range：0.04

%end；

%if(&power.>100 | &power.<0)%then %do；

%let error=1；

%put %str(ERROR：Power%'s range：0-100)；

%end；

%if &error.=1 %then %goto exit；

proc datasets nolist nodetails NoWarn lib=work；

delete fuction/memtype=data；

quit；

/*定义函数vv、c，用于计算AUC的方差、协方差 */

proc fcmp outlib=work.fuction.conversion；

function vv(theta，B，R，type)；

pi=constant('pi')；

%*对于观测变量为连续型，求AUC的方差；

if type=2 then v=theta/(R*(2-theta))

+2*theta*theta/(1+theta)- theta*theta*(1+R)/R；

%*对于观测变量为等级型，求AUC的方差；

if type=1 then do；

A=probit(theta)*sqrt(1+B**2)；

E=exp(-A*A/(2+2* B**2))；

g=-A*B*E/sqrt(2*pi*((1+B**2)**3))；

f=E/sqrt(2*pi*(1+B**2))；

v=f**2*(1+B**2/R+A**2/2)+g**2*(B**2)*(1+R)/(2*R)；

end；

return(v)；

endsub；

run；

proc fcmp outlib=work.fuction.conversion；

function C(theta1，theta2，B1，B2，r1，r2，R，type)；

A1=probit(theta1)* sqrt(1+B1*B1)；

E1=exp(-A1*A1/(2+2*B1*B1))；

g1=-A1*B1*E1/sqrt(2*constant('pi')*((1+B1**2)**3))；

f1=E1/sqrt(2*constant('pi')*(1+B1**2))；

v1=f1**2*(1+B1**2/R+A1**2/2)+g1**2*(B1**2)*(1+R)/(2*R)；

A2=probit(theta2)* sqrt(1+B2*B2)；

E2=exp(-A2*A2/(2+2*B2*B2))；

g2=-A2*B2*E2/sqrt(2*constant('pi')*((1+B2**2)**3))；

f2=E2/sqrt(2*constant('pi')*(1+B2**2))；

v2 =f2**2*(1+B2**2/R+A2**2/2)+g2**2*(B2**2)*(1+R)/(2*R)；

%*对于观测变量为等级型，求AUC的协方差；

if type=1 then c=f1*f2*(r1+B1*B2*r2/R+A1*A2*r1*r1/2)

+g1*g2*B1*B2*(r2**2 +R*(r1**2))/2/R

+f1*g2*A1*B2*r1*r1/2

+f2*g1*A2*B1*r1*r1/2；

%*对于观测变量为连续型，求AUC的协方差；

if type=2 then do；

v1=theta1/(R*(2-theta1))

+2*theta1*theta1/(1+theta1)- theta1*theta1*(1+R)/R；

v2=theta2/(R*(2-theta2))+2*theta2*theta2/(1+theta2)

- theta2*theta2*(1+R)/R；

/*&rvalue为查表所得，比如此例为rvalue=0.72 */

c=&rvalue.*sqrt(v1*v2)；

end；

return(c)；

endsub；

run；

optionscmplib=(work.fuction)； %*调用定义的函数；

data tworoc；

%**---参数输入----**；

zero1=2*vv(&theta1，&B1，&R，&type)； %*求得V0(Δ)中的：2V(θ1)；

one1=vv(&theta1，&B1，&R，&type)

+vv(&theta2，&B2，&R，&type)；%*求得V1(Δ)中的：V(θ1)+V(θ2)；

%*求得V0(Δ)中的：2C(θ1，θ1)；

zero2=2*C(&theta1，&theta1，&B1，&B1，&r1，&r2，&R，&type)；

%*求得V1(Δ)中的：2C(θ1，θ2)；

one2=2*C(&theta1，&theta2，&B1，&B2，&r1，&r2，&R，&type)；

alpha=&alpha；

side=&side；

theta1=&theta1；

theta2=&theta2；

r1=&r1；

r2=&r2；

B1=&B1；

B2=&B2；

R=&R；

type=&type；

power=&power；

power=power/100；

V0=zero1-zero2； %*求得V0(Δ)；

V1=one1-one2； %*求得V1(Δ)；

N_p=ceil((probit(1-alpha/side)*sqrt(V0)+probit(power)*sqrt(V1))**2

/((&theta1-&theta2)**2))；%*阳性个体数；

N_n=ceil(N_p*R)； %*阴性个体数；

R=N_n/ N_p；

power=round(100*probnorm((sqrt(N_p)*ABS(&theta1-&theta2)

-probit(1-alpha/side)*sqrt(V0))/sqrt(V1))，0.01)；

run；

data tworoc1；

set tworoc；

if type=2 then q='Continuous'；

if type=1 then q='Discrete'；

run；

/*结果输出*/

proc print data=tworoc1 label；

var alpha side q theta1 theta2 r1 r2 B1 B2 R N_p N_n power；

label alpha="Test significance level"

side="1 or 2 sided test"

q="Data Type"

theta1="Reference Test AUC"

theta2="New Test AUC"

r1="Correlation for Positive Group"

r2="Correlation for Negative Group"

B1="Test 1St.Dev.Ratio"

B2="Test 2St.Dev.Ratio"

R="Sample Size Ratio"

N_p="Positive Group Sample Size"

N_n="Negative Group Sample Size"

power="Power(%)"；

quit；

%exit：

%mend；

%tworoc(alpha=0.05，side=2，type=2，theta1=0.85，theta2=0.90，

r1=0.80，r2=0.76，B1=1，B2=1，R=4，power=80，rvalue=0.72)

SAS运行结果：

SAS 9.4阳性组样本量与nQuery Advanced的对应结果相差3，是因为nQuery Advanced中在连续型变量计算中，对r的取值与基于查表法提供的r值稍有不同(经验证前者r的取值约为0.727，而表格1中r的取值为0.72)。

图8 SAS 9.4 关于例4样本量估计的参数设置与计算结果