碳纳米管海绵导热性能的实验研究

刘心颖，林 欢，董 华

(青岛理工大学环境与市政工程学院，山东 青岛 266033)

1 前 言

从1991年日本研究实验室[1]发现碳纳米管(CNTs)以来，碳纳米管以其优异的力学、电学、热物理性能以及良好的化学性能受到研究者们的广泛关注[2, 3]，成为新时代最具发展潜力的纳米材料之一。为了实现碳纳米管材料的实际应用，定向控制碳纳米管的自组装工程技术成为了关键的一步。随着科技的发展，为了更好地满足社会生产的需求，一种碳基海绵——碳纳米管海绵，顺应时代的脚步孕育而生。

碳纳米管海绵通过改变以碳纳米管为基础的宏观结构，表现出高比表面积、高孔隙率、强韧的机械强度、优异的导电性能及电化学性能，在能源存储[3-5]、催化[6]、吸附[7]、复合保温材料[8, 9]等领域有广泛的应用前景，使其在学术领域引起了科研工作者的极大关注和研究。从保温性能的角度出发，碳纳米管海绵作为一种新型的碳纳米保温材料，具有低导热系数，起到隔热、绝热的作用。使用保温材料对减小能耗、充分利用资源，以及促进可持续发展具有深远影响和非凡意义。针对不同场合的保温需求有所不同，无论是建筑、航天航空、海洋还是服饰材料，具有隔热绝热特性的多孔材料都在扮演着重要角色[10]。碳纳米管海绵作为最具有前途的保温材料之一，导热性能的实验研究显得尤为重要。Gui等[9]制备出的碳纳米管海绵在200～360 K温度下，导热系数小于0.15 W·m-1·K-1，具有良好的隔热性能。但是，碳纳米管海绵为何会呈现低导热系数，仍有待进一步探索。据有关文献报道[11]，通过冷冻干燥法制备得到的石墨烯-碳纳米管复合海绵导热率低至0.021 W·m-1·K-1，和空气的导热率(0.026 W·m-1·K-1)在一个数量级上，然而这种碳海绵中片层之间仅为简单的物理接触，这使得其机械强度不尽如人意。Baetens等[12]报道了传统气凝胶材料被作为建筑热绝缘材料应用在节能建筑中，而传统气凝胶材料的韧性普遍较小，环境敏感且生产成本高，存在无法承受荷载的风险。相比之下，碳纳米管海绵结构具有较高的灵活性和韧性，能够在热绝缘材料领域里满足更多场合的需求，这意味着碳海绵导热性能的研究具有长远的价值。

目前，在国际上对碳纳米管海绵的研究集中在力学、电化学和吸附性能方面，在导热方面主要通过增加碳纳米管海绵复合材料的导热性能以提高其在相关领域的散热能力为主[13, 14]，而对其在保温隔热方面的报道颇少。为了实现碳纳米管海绵在各个领域的应用，了解其在室温下的热机制属性，为其作为一种先进的保温材料提供理论依据和数据支撑，本工作将采用瞬态电热(TET)测量技术对其导热性能进行研究，并结合SEM照片，从微尺度传热的角度分析碳纳米管海绵的导热特征。

2 实 验

2.1 实验材料

热性能实验中使用的碳纳米管海绵样品购自江苏先丰纳米材料科技有限公司，如图1所示。该碳纳米管海绵由气体碳源通过化学气相沉积法制备而成，密度为10 mg·cm-3，孔隙率为99%，碳纳米管内径为10～20 nm、外径为30～50 nm。图2为该样品的SEM照片，由图2c可以清楚地看到碳纳米管海绵样品由很多丝状物无序缠绕纵横交织在一起，其孔隙空间布局是由无数多壁碳纳米管及管束无序塔接组成，单个孔隙大小从几纳米到几十微米不等。

图1 碳纳米管海绵样品照片Fig.1 Image of carbon nanotube sponge sample

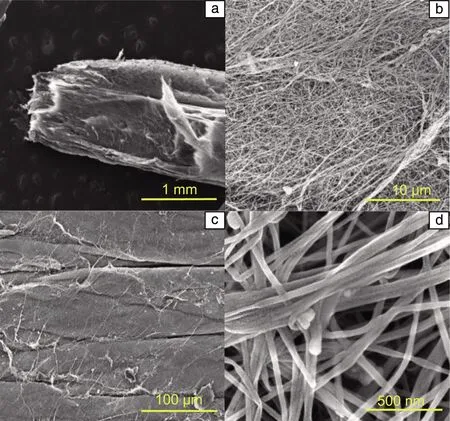
图2 碳纳米管海绵样品的SEM照片Fig.2 SEM images of carbon nanotube sponge sample

碳纳米管海绵中存在大量的孔隙，从微观角度上来看，这些孔隙的存在形式取决于固体材料在孔壁和孔棱的分布形式，这也决定着多孔材料的各种性能。碳纳米管海绵孔隙包含碳纳米管相互堆积形成的堆积开孔和多壁碳纳米管本身的中空管腔结构。当碳纳米管顶端为开口状态时，管腔结构形成的是开孔；反之封闭状态时，形成的是闭孔。毫无疑问，这些不同的孔隙结构对材料的导热能力有着本质影响，这一点将在后面章节进行分析。在文献[8]中，降低碳源的给进速率将有助于提高碳纳米管海绵的孔隙率，但是不同孔隙率的碳纳米管海绵都具有相似的孔隙分布趋势，均存在微孔、中孔以及较大直径的堆积孔，密度越低的碳纳米管海绵则具有更大的堆积孔。

事实上，碳纳米管海绵的孔隙率大小更依赖于较大孔径的堆积孔。从几何的角度来看，大多数的多孔材料都是由骨架固体物质进行非等同单元无规则堆积而成的，包含着不同数量的面和棱围成的具有不同大小和形状的孔隙。有研究表明[15]，即使是最紊乱的泡沫堆积方式也遵循支配蜂巢等孔隙有序规则材料一样的拓扑规律。简单来说，碳纳米管纤维在空间上可被看作线，作为孔棱；线与线交织形成孔穴的顶点，共同组成孔穴壁面，根据Euler定律[15]，在三维孔穴集合体中，顶点数V、面数S、棱数E和孔穴数H关系为：-H+S-E+V=1。

另外，碳纳米管由于范德华力作用[16]而在相互交织重叠处形成“结头”，如图2d所示，这种交错塔接的网络结构也使得碳纳米管海绵在宏观上呈现出良好的稳定性。

2.2 实验原理

瞬态电热(TET)测量技术[17]是一种测量材料热扩散系数的方法，被测量材料可以是导电、半导或非导电一维导热结构的固体材料，图3为TET测量技术实验原理图。这种方法具有快速、准确、有效的测量特点，其准确性已经通过研究现有材料的已知热扩散系数得到证实。研究表明，TET测量技术对材料的热表征结果与已知参考值的偏差小于5%[18]。由于碳纳米管海绵样品的尺寸远远大于纳米数量级的内部孔隙，这使得焦耳加热作用对测试样品产生的体积热在空间上是均匀分布的，而且该样品可以被近似看作一维导体材料。因此，可通过TET测量技术快速准确地得到样品的热扩散系数，这种可行性在前人的试验研究[19]中已经得到充分证实。下面将用理论分析结合实验来解释如何获得样品的有效热扩散系数。

图3 瞬态电热测量技术实验原理图Fig.3 Schematic diagram of TET technique

实验前将样品搭接到两端电极上，通过对样品施加一个阶跃性直流电流诱导焦耳加热，使得样品的温度存在一个小的上升，导致其电阻改变，进而产生电压波动。在这个电加热过程中，被测量样品会在瞬间时域内达到热稳定状态，利用温升(电压时间变化)和传热的数学模型最终可得到样品的热扩散系数。由于整个电加热实验都处于密闭的真空(0.3～0.4 Pa)腔体内，因此可忽略热对流对实验测量结果的影响，仅需考虑热传导、焦耳加热和环境热辐射对实验结果的作用。在TET测试实验中，示波器显示电压变化Vsample和样品平均温度变化可表示为式(1)和式(2)：

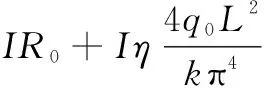
(1)

其中，I为负载电流；R0为样品电阻；L为样品长度；k为样品导热率；αeff为有效热扩散系数；q0为单位体积的加热量，在整个实验过程中为定值；η为样品电阻温度系数；t为时间。理论上样品归一化平均温升T*(t)可表达为式(2)：

(2)

事实上，实验中直接测量温升大小是比较困难的，因此通过电压的变化将归一化温升表示为T*exp=(Vsample-V0)/(V1-V0)，式中V0、V1分别为样品两端的初始电压和最终的稳态电压。然后，将温升实验值T*exp和理论值T*进行数据拟合，最终选取拟合最佳结果作为该样品的有效热扩散系数。为了降低实验误差、提高数据准确性，实验中对每组样品进行多次热扩散系数测量，接着计算得到一个平均值作为该测量样品的最终有效热扩散系数值αeff。

2.3 热辐射影响的去除

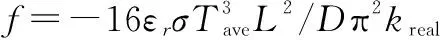
2.4 实验仪器和步骤

本文中主要使用到的实验仪器为偏光显微镜(型号DM2700P，德国Leica微系统有限公司)、数字示波器(型号DSO-X3052A，美国Agilent科技有限公司)、数字万用表(型号15B+，美国Fluke公司)、微电流源(型号KEITHLEY 6221，美国KEITHLEY仪器公司)等。

首先用刀片将块状碳纳米管海绵朝一个传热面切成均匀等厚长条状样品CNTS1、CNTS2。接着，将样品悬浮搭接在两个洁净的铝片和硅片之间，并用夹子将其紧紧固定在基底上，以保证样品和硅电极之间具有良好的热接触和电接触。电极通过铝螺钉和硅胶层相互连接，使得两个铝电极组成的样品夹附在真空腔体内。为了输入电流并记录电压输出，将电流源和示波器并联到铝电极上。通过输入不同大小的电流，同时使用示波器监测每个电流下时域电压波动响应，最终获得电压-时间曲线波形图。之后切断负载电流并缩短样品的测量长度，并进行下一组长度样品的实验测量。对于样品CNTS1，实验将该样品分成了8个长度进行测试，编号分别为CNTS1-1、CNTS1-2…CNTS1-8，具体样品尺寸如表1所示。

表1 样品CNTS1和CNTS2的尺寸参数Table 1 Size parameters of samples CNTS1 and CNTS2

3 结果及分析

3.1 利用TET技术测量热扩散系数

以碳纳米管海绵CNTS1为例，下面将详述样品热扩散系数的表征过程。样品CNTS1-1长为8.50 mm、宽为0.62 mm、厚为0.66 mm，对其施加10 mA的直流电流，此时样品的平均电阻为62.45 Ω，并且得到一个压降比为0.91%的电压波形图(如图4)，示波器显示电压随着时间的增加而快速下降随后达到一个平衡状态，这意味着电流诱导样品焦耳加热产生的温升很小。

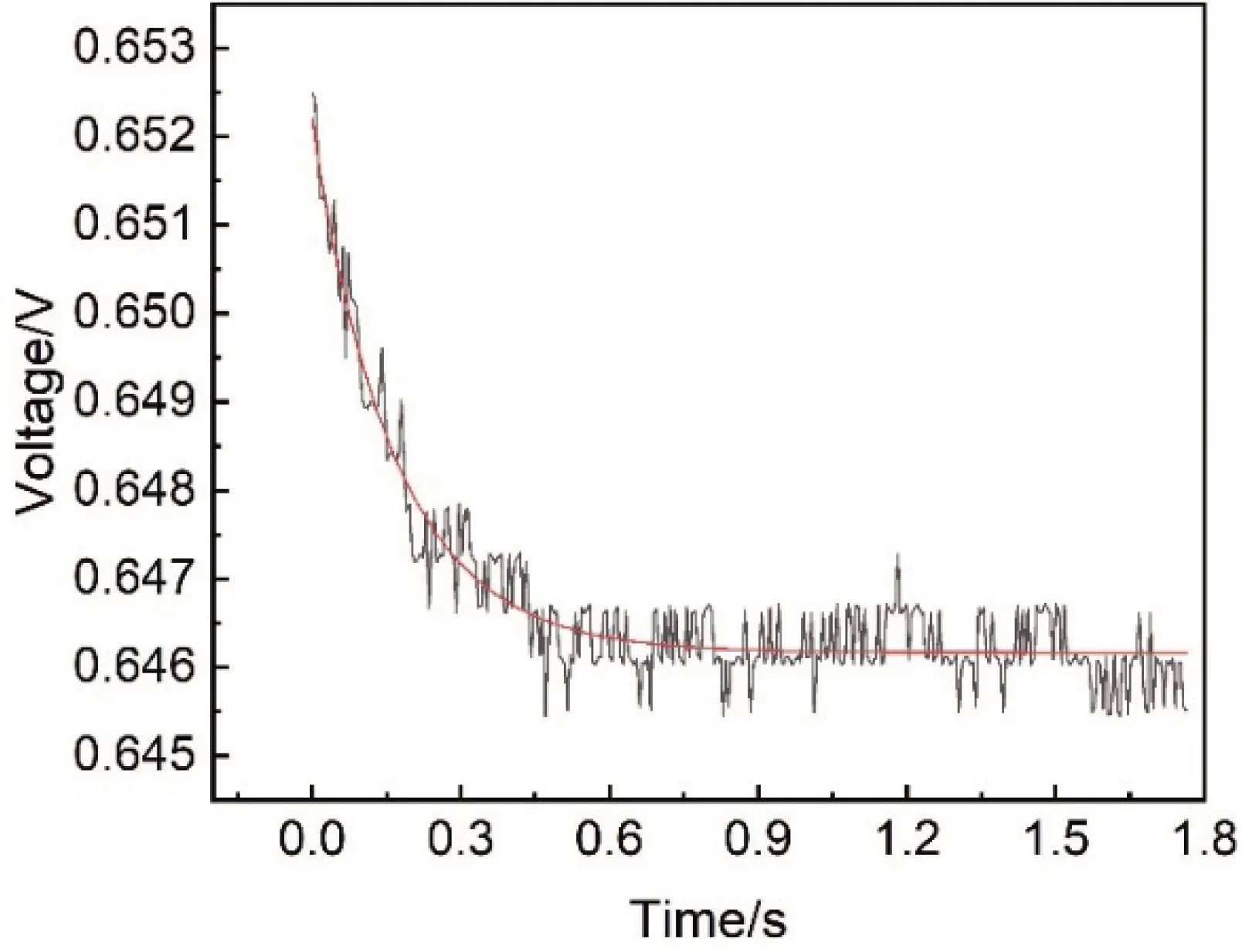
图4 样品CNTS1-1电压波形图Fig.4 Voltage oscillogram of sample CNTS1-1

表2 样品CNTS1的在瞬态电热测量实验中的参数Table 2 The measurement parameters of sample CNTS1 in TET experiment

图5显示了样品CNTS1的αeff/L2线性拟合图。由于温升较小，样品的有效热扩散系数与αeff和L2成线性正相关。当L2趋近于0时，即可得到样品CNTS1的真实热扩散系数αreal为1.14×10-5m2·s-1。

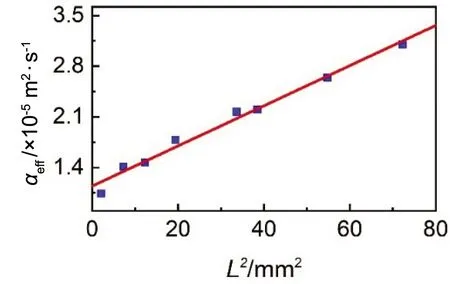
图5 CNTS1样品的有效热扩散系数αeff和L2的线性拟合图Fig.5 Linear fitting of the effective thermal diffusivity change against L2 for sample CNTS1

3.2 碳纳米管海绵的骨架热扩散系数

事实上，前面章节所提到的碳纳米管海绵的真实热扩散系数αreal是海绵体骨架和海绵体内空气热传导共同作用的结果。因此，为了探求碳纳米管海绵样品的本征热扩散系数，本研究引入了Schuetz等[21]的多孔介质导热模型，得到碳纳米管海绵样品的骨架导热率理论表达式为：

kintr=3kreal/φ

(3)

其中，kintr为碳纳米管海绵的骨架导热率；kreal为碳纳米管海绵的真实导热率；φ为多孔介质的固相体积分数，在本实验中所使用的碳纳米管海绵样品中该参数是非常小的。

Krishnan等[22]在研究中已证实当多孔材料样品的固相体积分数很小时(φ<6%)，可以采用式(3)对样品骨架导热率和真实导热率的关系进行表述。Liu等[17]在多孔材料的固相体积分数未知的情况下，通过使用该导热模型确定了石墨烯泡沫多孔材料的骨架导热率。从本研究对象出发，孔隙率达到99%的碳纳米管海绵样品完全满足该导热模型的适用条件。以测试样品CNTS1为例，引入导热率和热扩散系数关系表达式组：

(4)

式组中，ρCNTs表示组成碳纳米管海绵的多壁碳纳米管的骨架密度，该参数由生产厂家南京市先锋纳米有限公司提供，约为2100 kg·m-3；cp为多壁碳纳米管比热容[23]，取值709 J·kg-1·K-1。于是，方程可改写成αintr=3αreal，并计算得出样品CNTS1的本征热扩散系数αintr为3.43×10-5m2·s-1。进一步计算结果如表3所示，即碳纳米管海绵样品的真实热扩散系数为1.01×10-5～1.14×10-5m2·s-1，本征热扩散系数为3.03×10-5～3.43×10-5m2·s-1。

表3 碳纳米管海绵样品在TET测试技术下的热表征结果Table 3 Thermal characterization results of carbon nanotube sponge samples by TET testing technique

进一步考虑该样本的骨架导热率kintr和真实导热率kreal。根据方程组(4)，在其他物性参数均已知的情况下，将不难得出样品的骨架导热率为45～51 W·m-1·K-1，而真实导热率则可达到0.15 W·m-1·K-1。

3.3 碳纳米管海绵的界面换热系数

在隔热保温的实际运用中，除了材料本身的导热情况非常重要之外，由于多孔材料孔隙率高，具有较大的比表面积和良好的流通性，所以当有流体流过材料时，材料的表面热交换作用也尤为重要。但是，这并非本实验研究的重点，因此本节对碳纳米管海绵的界面换热系数进行简单的介绍。

重庆大学王济平[24]通过建立多孔泡沫材料表面传热性能实验台对多种泡沫材料进行表面换热特性研究，发现多孔材料表面换热系数随流体流速的增大而增大，随孔隙率的增大而减小；并且在相同流体流速下，表面换热系数随固体骨架导热率增大而增大，其中石墨泡沫在3 m·s-1的空气流扰动下，其表面换热系数达到了475 W·m-2·K-1以上。这些研究结果与文献[25-27]中多孔材料表面传热特性规律一致，因此也同样适用于碳纳米管海绵界面换热系数的特征描述。

当孔隙分布均匀时，碳纳米管海绵的孔隙率越大，孔穴所占的体积就越大，其固体骨架结构的体积占比减少，这样一来，就削弱了固体结构对气流的扰动能力，进而导致表面换热能力减小。固体骨架导热率的大小对泡沫材料的界面换热系数也有着本质影响，对于由高导热固体材料组成的碳纳米管海绵，当热量通过碳纳米管骨架流入碳纳米管海绵时，传热热阻相对较小，因此其表面换热能力更强。这无疑对碳纳米管海绵的隔热保温效果是不利的，同时对如何降低碳纳米管海绵的传热系数有了启发。研究人员[28]对隔热瓦(一种与碳纳米管海绵有着类似纤维固体骨架三维塔接结构的多孔材料)表面喷涂了具有高辐射率的玻璃涂层，当表面温度高达900 K并历时800 s后，背面温度仍可保持在289.6 K。这说明高辐射涂料层反射和吸收了表面的大部分热量，进一步缓解了材料的隔热压力。

3.4 碳纳米管海绵的热运输机理

在前文中描述了碳纳米管海绵骨架和孔隙等结构特征，接下来将从微观层面分析它们对传热的响应方式。一般来说，多孔材料[29]是一种由两相或多相物质组成的共同空间，热量传递过程比较复杂，其等效导热率的结果主要取决于材料的形态结构和物性这两方面，如孔隙率、孔隙分布、比表面积、真密度、体积密度等。Alam等[30]通过激光脉冲测定法研究分析了12种不同孔隙率的石墨泡沫材料，其表观密度为0.23～0.65 g·cm-3、有效导热率为3.88～174.9 W·m-1·K-1，揭示了材料的容积性质对石墨泡沫导热性能的影响。根据相关报道[31]，多孔介质中多相组成结构的物性差别会导致各相物质对导热性能方面的贡献大小不同，当多孔材料骨架结构具有高导热率时，流体对材料导热性能作用较小。

碳纳米管海绵是一种典型的多孔介质。在碳纳米管海绵中，热量传递主要包括骨架间的声子碰撞和孔隙间的热辐射效应及固气两相之间的对流换热[20]。由于本实验研究是在真空环境下进行的，并剔除了热辐射效应的作用，因此在本节不讨论对流和热辐射的影响，仅从纯导热过程进行分析。

碳纳米管海绵中存在大量的孔隙，不管是纳米级的中空孔隙还是微米级的堆积孔隙，这些孔隙的存在都严重阻碍了空气在海绵中的热对流，当孔隙直径小于空气分子的平均自由程时，空气分子之间的微小对流传热作用将消失，使得材料导热率降低。有研究显示[15]，泡沫材料的时效性会影响其导热率，这是因为多孔材料中既存在开孔又存在闭孔，经过一个时间期限，封闭的气体从闭孔中扩散出来，低密度的空气扩散进去，将会使得泡沫材料的导热率增加达50%。因此，开口孔穴分数也会在小范围程度上影响碳纳米管海绵热运输的结果。

另外，碳纳米管海绵内部的孔隙和骨架之间的相界面可能会阻碍声子热运输，并且使得导热路径变得曲折，这也是为什么单根碳纳米管导热率非常高(k=6000 W·m-1·K-1)[32]，而碳纳米管海绵的却很小的主要原因。图6为碳纳米管海绵骨架材料在无空隙和孔隙分布均匀理想的情况下的热传递过程，正是因为孔隙的存在，导致了内部晶格的缺失，增大了声子在骨架结构中的传导阻碍，进而降低了碳纳米管海绵的导热率。当孔隙排布随机时，孔隙使得热流流动方向更为频繁地改变，大大增加了接触热阻，对降低材料导热性能的效果更明显。有研究表明[11]，多孔介质的有效导热率不仅随孔隙率的减小而增大，并且与孔隙的均匀度也有密不可分的关系，通过模拟计算可以得出有效导热率是孔隙均匀度的增函数。

图6 碳纳米管海绵骨架结构的热传导模型Fig.6 Heat transfer model of carbon sponge skeleton structure

理论上，碳纳米管海绵材料的骨架导热率可以由Debye模型得到：

(5)

其中，cP为多壁碳纳米管的比热容，ν为声子的平均移动速率，l为声子的平均自由程。

在本实验中，重点考虑碳纳米管海绵本身的物理结构及结构缺陷等因素。如图2a和2b所示，测试样品的传热表面存在大量无规律褶皱，且由于测试样品是从1 cm×1 cm方块样品上切割下来的，样品边缘存在着不可避免的粗糙度。在热量传递的过程中，能量的传输依赖于声子进行点阵振动的传播，而这些结构缺陷使得在声子传播中形成声子散射[33]，大量落在传热表面，导致了声子平均自由程减小，从而阻碍了声子的热运输过程，进一步降低了碳基材料的导热率。同时，碳纳米管海绵本身无序排列结构内的弱范德华力造成了低模量和毗邻原子振动的弱耦合，也缩短了声子平均自由程，使得其传热效率大大降低。裴娱[34]通过改变多壁碳纳米管管束的生长方向制备了具有高导热率的碳纳米管复合阵列三维宏观体，从而证实了管束顺长整齐度的提高可以有效降低样品的接触热阻。观察本实验样品传热面的结构表征，除了声子散射的作用，碳纳米管交织“结头”形成的无数个纳米级的点接触，造成了无数个接触热阻，导致了样品的低导热性能，如图2d所示。

4 结 论

本实验介绍了采用瞬态电热测量技术对碳纳米管海绵样品在室温下导热性能的探究过程，测定了样品真实热扩散系数为1.01×10-5～1.14×10-5m2·s-1。考虑到碳纳米管海绵材料的多孔骨架结构，本实验借助 Schuetz多孔介质导热模型得到了碳纳米管海绵的骨架热扩散系数约3.03×10-5～3.43×10-5m2·s-1，真实导热率可达到0.15 W·m-1·K-1，这使得它成为一种非常有前途的隔热材料。通过样品SEM照片解释了碳纳米管海绵低导热率的主要原因：由于材料表面的结构缺陷和本身高孔隙率，较大的接触热阻和传热表面边缘的声子散射是影响热运输的重点所在。本实验结果将为碳纳米管海绵在隔热保温领域的应用提供重要的理论支撑，对碳纳米管宏观体后续的热运输研究具有指导性价值。