世界不确定性指数与中国股市波动率预测研究

计 玉， 王 璐， 郝建阳， 张 莉

（西南交通大学数学学院，成都 611756）

伴随着2020年新冠疫情的全球大流行，全球经济正处于结构转型、产业优化等关键时期，许多国家陆续大量出台了货币、财政等宏观经济政策来促进经济稳定高速发展. 然而，国家之间经济政策的不均衡性、国际贸易及进出口等方面的摩擦进一步加剧了世界经济不确定性的增加. 与此同时，中国股票市场作为新兴股票市场越来越受到国际局势的影响，特别是当前中美关系的摩擦加剧更增加了股市的波动. 因此，在全球化背景下，理清世界不确定性与中国股票市场的关系，研究全球经济政策不确定性对中国股市波动的影响具有较好的理论及实际意义. 为填补在衡量经济政策不确定性方面研究的空白，Ahir等［1］为那些自1996年第一季度以来一直使用经济学人智库国家报告的143个国家建立了一个新的不确定性指数——世界不确定性指数（World Uncertainty Index）. 国内鲜有文献研究世界不确定性指数对股票市场波动的影响，本文尝试使用世界不确定性指数作为宏观经济变量研究其对上证指数波动率的影响.

线性模型是研究股票金融市场波动率预测的经典模型，然而像1987 年出现的“黑色星期一”等事件，经济学家们无法用传统的线性模型（如自回归模型AR（p）、自回归滑动平均模型ARMA（p，q））来解释股票市场的突变，但是非线性特征的存在却受到了经济学家们的关注. 随着对非线性特征的不断研究，非线性模型也逐渐开始被应用到金融市场. 非线性机制转化模型是在研究非线性金融时间序列中比较成功的模型，一般由3 种常见的模型组成：马尔可夫机制转换模型、阈值模型和平滑转换回归模型（STR）. STR 模型是Granger 和Teräsvirta［2］提出的非线性模型，相比于马尔可夫机制模型无法观测到状态变量和阈值模型的转化状态为可观测到的离散值，STR 模型能够刻画出研究变量处于不同的状态，以及不同状态之间的非线性转换，并且STR模型处于2个极端状态下的变化是平滑. Teräsvirta［3］在1994年又进一步对STR模型进行完善并进行了实证分析. McMillan［4］研究了股票市场收益与宏观变量之间是否存在非线性关系，以及这种非线性关系是否可以用于预测的改进，结果表明STR 模型不仅刻画出宏观变量和股票波动率的非线性关系并且提高了股票波动率预测的精度. 所以本文采用STR 模型来刻画股票收益率与宏观变量之间的非线性关系.

由于宏观变量和股票波动率之间存在数据不同频率问题，Engel 等［5］提出的GARCH-MIDAS 模型很好地解决了这一问题，并将模型用于美国股票市场波动与宏观经济之间的研究. 该模型将收益率分解为短期高频成分与长期低频成分，是目前研究宏观经济与股票市场波动关系的较好方法. 国内外学者也多以宏观经济变量为研究变量，运用多因子GARCH-MIDAS 模型将波动率分解为长期成分和短期成分，对股市进行了预测［6-8］；郑挺国和尚玉皇［9］研究结果表明，GARCH-MIDAS模型在研究过程中能够利用更为丰富信息，较好地拟合股票市场，描述宏观经济与股市波动之间的关系.

基于以上认识，本文的不同之处在于：1）尝试引入世界不确定性指数作为宏观经济变量，研究全球政治政策和经济不确定性因素对我国股市波动的影响；2）在GARCH-MIDAS模型的基础上结合非线性模型STR构建出模型LSTR-GARCH-MIDAS，该模型不仅能够解决数据之间存在不同频率的问题，而且能刻画出宏观经济变量与金融时间序列之间存在的非线性特征.

1 模型介绍

1.1 GARCH-MIDAS模型

Engle等将Ghysels和Santa-Clara［10］提出的混频数据抽样（MIDAS）回归模型引入到广义自回归条件异方差（GARCH）模型中，提出了GARCH-MIDAS模型建模方法，并将收益率表示为：

其中：ri,t表示第t月内第i个交易日的收益率；Ei-1,t(ri,t)表示在第t月内第i-1个交易日之前的信息集的条件方差；hi,t为GARCH（1，1）模型拟合的波动率短期成分；τt为波动率长期成分；残差εi,t为服从均值为0方差为1 的标准正态分布的随机干扰项，即εi,t|Φi-1,t～N(0,1)，其中Φi-1,t为第t月内第i-1 个交易日的信息集合；Nt为第t月的交易天数. 将公式（1）改写为：

其中：μ表示为均值；波动率短期成分hi,t服从GARCH（1，1）模型，即：

其中：α与β为参数.

用已实现波动率RVt来刻画长期波动率成分τt，表示为式（4）：

其中：K为波动率长期成分中的最大滞后阶数；m,θ,ω1,ω2均为待估参数；φk(ω1,ω2)为权重函数，RVt-k为已实现波动率，分别由式（5）、（6）表示.

GARCH-MIDAS模型由式（1）～式（6）共同构成，也称已实现波动率的GARCH-MIDAS模型.

1.2 GARCH-MIDAS-X模型

如前文所述，宏观经济变量对股票价格具有重要影响，与股票价格波动的长期成分密切相关，考虑在上述的GARCH-MIDAS模型中引入宏观经济变量，即在波动率的长期成分中用宏观经济变量来替代已实现波动率. 由于宏观变量数据有正负之分，故对τt作对数变换得log(τt)，即将（4）式改为（7）式得到：

其中：xt-k表示宏观变量滞后K期；m,θ,ω1,ω2均为待估参数. 因此，纳入宏观经济变量的GARCH-MIDAS模型（GARCH-MIDAS-X）由式（2）、（3）、（5）、（6）和（7）构成.

1.3 STR模型

STR模型最先由Granger 和Teräsvirta 1993年提出，模型可以刻画出研究变量处于不同的状态以及不同状态间的非线性转换，对于变量yt，STR模型的一般形式为：

其中：G(st;γ,c)表示转换函数，定义为值域［0，1］上的连续有界函数. 转换函数中共有3类参数：st为过渡变量，参数c为位置参数决定了转换函数发生变化的位置，参数γ则为平滑参数，表示转换函数从状态0到状态1的转变速度；xt为解释变量组成的向量，即xt=(1,x1t,…,xpt)′；φ′=(φ0,φ1,…,φp)′和θ′=(θ0,θ1,…,θp)′为有p+1个变量组成的参数向量；εt为独立同分布的误差序列. 根据转换函数一般表达为逻辑函数（9）和指数函数（10），对于逻辑函数（9），模型为逻辑平滑转换回归（LSTR）模型，此时G(st;γ,c)是关于st的单调递增函数.

转换函数为指数函数（10）时，模型为指数型平滑转换回归（ESTR）模型. 与式（9）不同的是，转换函数为指数函数时，G(st:γ,c)为偶函数.

1.4 STR-GARCH-MIDAS-X模型

平滑转换回归广义条件异方差模型（STR-GARCH-MIDAS-X）作为GARCH-MIDAS-X 扩展模型，在GARCH-MIDAS-X模型的基础上结合非线性模型STR，不仅解决了经济变量不同频率造成信息丢失影响预测精度的问题，还考虑到了宏观经济变量和收益率之间的非线性结构特征. 与GARCH-MIDAS-X 模型相比，该扩展模型用STR模型中非线性结构转变回归替换波动率长期成分中的线性回归得到新的波动率长期成分τt′，并对τt′ 作对数处理，得到模型的具体结构如式（11）：

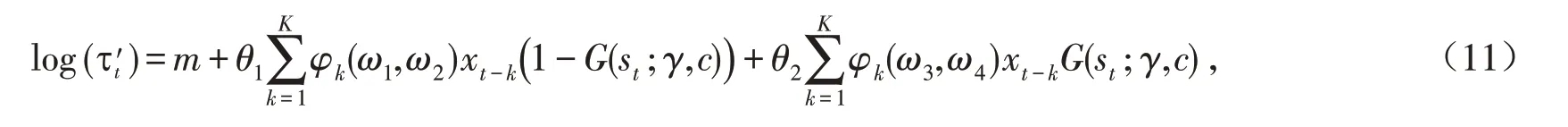
其中：m,θ1,θ2,ω1,ω2,ω3,ω4均为待估参数. 因此，STR-GARCH-MIDAS-X模型由式（2）、（3）、（6）和（11）构成.根据模型的转换函数不同又将模型分为逻辑平滑转换回归-混频广义条件异方差（LSTR-GARCH-MIDAS-X）模型和指数平滑转换回归-混频广义条件异方差（ESTR-GARCH-MIDAS-X）模型.

本文采用极大似然估计法对上述非线性模型STR-GARCH-MIDAS-X 进行参数估计，其极大似然函数为：

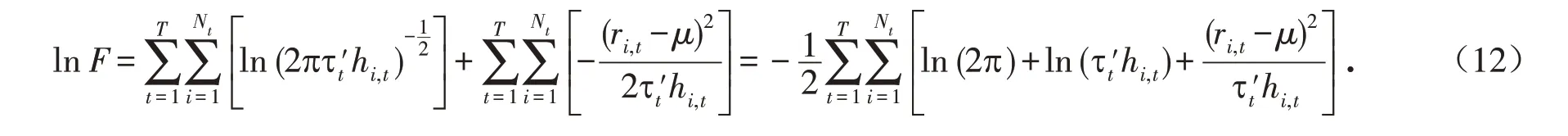
2 非线性检验

在建立非线性模型之前要先进行非线性检验，对转换函数G(st;γ,c)来说，若γ=0 时，转换函数G(st;γ,c)的值为常数，模型就不再存在非线性特征. 所以检验模型是否具有非线性特征通常是借助转换函数G(st;γ,c)来进行的. 依据Shuairu等［11］2015年的研究，选取已实现收益率RVt来替代条件方差来检验模型是否存在非线性特征. 将公式（8）中的转换函数G(st;γ,c)在γ=0 处进行三阶泰勒展开得到辅助回归方程为：

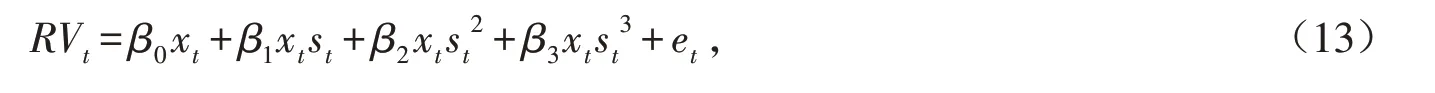
其中：et为误差项，对公式（8）进行非线性检验即对辅助方程进行非线性检验. 显然，非线性检验的原假设为H01:β1=β2=β3=0，若拒绝原假设H01即存在非线性特征. 当原假设H01成立时，使用Luukkonen等［12］提出的LM检验统计量来实现非线性检验，本文中LM统计量渐近服从χ2(3K+3)分布，其中K为受约束参数个数，与长期波动成分中的滞后阶数相同，通过基于AR（K）模型拟合STR-GARCH-MIDAS-X 模型中的波动率长期成分和Akaike信息准则（AIC）、贝叶斯信息准则（Bayesian Information Criterion，BIC）来确定的. LM统计量表达式如下所示：

其中：SSR0为原假设成立时的残差平方和；SSR1为拒绝原假设时的残差平方和；N为观察值个数. 通过辅助回归方程（13）做进一步检验来选择转换函数G(st;γ,c)的形式：

原假设H02、H03和H04同样是通过计算LM统计量来实现检验. 在拒绝原假设H01以后，H03的p值最小，转换函数选择指数函数，在拒绝原假设H01条件下的其余情况，转换函数选择逻辑函数.

3 实证结果研究

3.1 数据和描述性统计

本文采用的数据样本为上证指数日度数据和Hites Ahir 等建立的世界不确定性指数（WUI）月度数据.上证指数的样本区间为从1991年1月2日到2020年3月21日（共7149个数据），数据来自英为财情. WUI为该时间段对应的月度数据（共351 个数据），数据来自经济政策不确定性网站（http：//www.policyuncertainty.com/wui_quarterly.html）. 根据收盘价计算出收益率，即rt=ln(pt)-ln(pt-1)，t=1,2,3,…，其中rt为t时刻的收益率，pt表示上证指数在第t天的收盘价. 在建模的过程中使用WUI的一阶差分序列（记为X）作为建模变量，上证指数收盘价和收益率时序图，以及WUI和对数差分后的WUI时序图如图1所示.

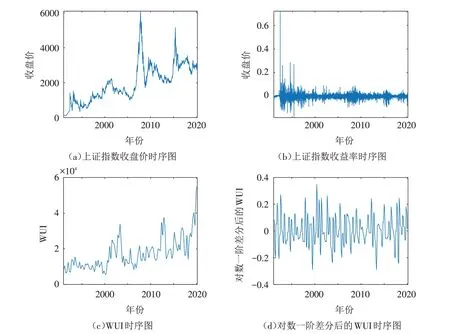
图1 时序图Fig.1 Sequence chart

表1给出了上证指数收益率的描述性统计，可以看出收益率序列的均值接近零，从峰度和偏度来看，该收益率序列具有过度的峰度和右偏态，并且Jarque-Bera（J-B）统计量显著，这表明收益率序列不服从正态分布，并且存在“尖峰厚尾”的特征. 单位根检验是检验序列平稳性的常用方法，其中最经典的方法为Augmented Dickey-Fuller（ADF）检验. 由表1中ADF检验结果知，在1%显著性水平下该统计量拒绝原假设，即我国上证指数收益率序列rt是平稳序列.

表1 上证指数描述性统计Tab.1 Descriptive statistics of the Shanghai Composite Index

在确定上证指数收益率序列是否平稳后，还需检验宏观变量的平稳性. 本文中使用ADF 检验和Phillips-Perron（P-P）检验来检验宏观变量的平稳性. 表2 为对宏观变量X做平稳性检验的结果，可以看出无论是ADF 检验还是P-P 检验都在5%显著水平上拒绝原假设，即宏观变量X为平稳序列，可以进行后续的建模分析. 通过宏观变量基于AR 模型拟合STR-GARCH-MIDAS-X模型中的长期波动成分和AIC、BIC准则选择模型的滞后阶数为K=6.

表2 宏观变量的平稳性检验Tab.2 Stationary test of macroscopic variables

3.2 非线性检验

表3 宏观变量对上证指数价格波动具有非线性影响的检验结果Tab.3 The tests of non-linear influence of macroscopic variables on Shanghai Composite Index price fluctuations

由表3可以看出，选择宏观变量X的滞后一期观测值xt-1作为转换函数G(st;γ,c)中的转换变量st，说明上证指数波动率的结构转换取决于宏观变量滞后一期观测值. 原假设为H01时拒绝原假设，即宏观变量X对上证指数波动具有非线性影响，并且原假设为H03时的p值并不是原假设中的最小值，所以选择LSTR模型来刻画宏观变量与上证指数波动率的非线性关系.

3.3 样本内估计结果

选取1991年1月2日到2010年6月24 日之间共4773 个数据作为样本内估计数据，逻辑函数作为转换函数，建立LSTR-GARCH-MIDAS-X 模型，根据式（12）所构造的对数似然函数，对参数进行极大似然估计. 并且同时对GARCH-MIDAS 模型和GARCHMIDAS-X 模型的参数进行了估计，参数估计结果见表4.

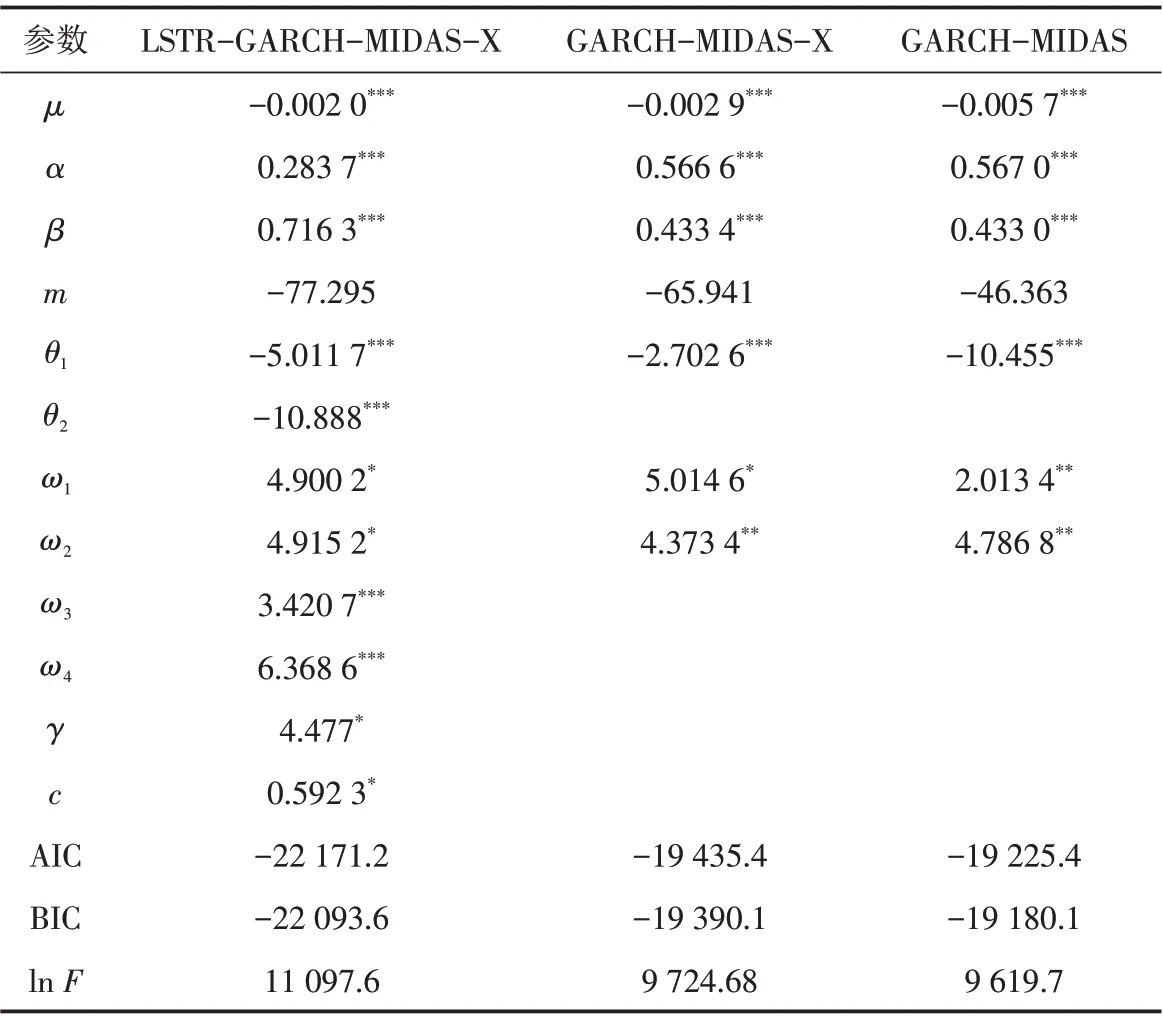
表4 参数估计结果Tab.4 The estimation results of parameters

从参数估计结果中可以看出：在3 个模型中除去长期成分的常数项m不显著外，其余所有参数均在10%显著水平上具有显著性，表明上述模型在样本内能够较好地拟合上证指数收益率. 参数α和参数β都大于零并且在1%的显著性水平下拒绝原假设，说明上证指数收益率历史波动信息影响着当期波动［13］. GARCH-MIDAS-X 模型中参数ω1和ω2的估计值都大于1，说明随着滞后时间的增加，宏观变量的权重系数φk的值减小，即越靠近当前时间，宏观变量的变化对上证指数波动率的影响也越大［14］. 模型LSTR-GARCH-MIDAS-X中参数γ=4.477 度量了转换函数的转变速度；位置参数c=0.592 3 表明了上证指数收益率上升和下降转变的临界水平，对数收益率低于0.592 3时，股票收益率处于上升状态，反之，则判断股票市场处于下降状态. 也说明宏观变量WUI对上证指数价格波动存在非线性影响，上证指数收益率并不会一直处于上升或下降的状态［15］.

AIC、BIC和对数似然函数值（lnF）用于模型的选择，AIC、BIC值越小，表明模型的拟合程度越好，lnF的值越大，也表明模型的拟合度越高. 由模型相对应的AIC、BIC和lnF值来看，都表明了非线性LSTR-GARCHMIDAS-X模型对于上证指数波动率样本内的拟合效果在3个模型中最好.

3.4 样本外预测

选取2010年6月25日到2020年3月31日共2376个数据作为样本外预测数据，得到模型的预测值后与波动率的真实波动比较，图2给出了模型关于上证指数波动率预测的效果图，蓝色为真实波动率，红色为模型预测波动率.

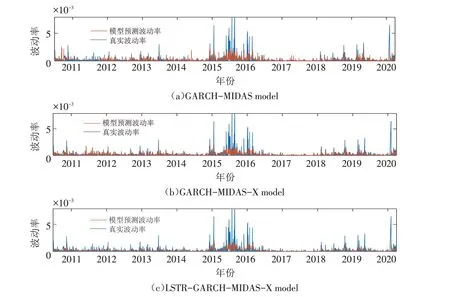
图2 真实波动和预测波动走势图Fig.2 Trend charts of real and forecast volatilities

本文通过损失函数来判断模型对波动率的预测能力，损失函数越小，表明模型的预测效果越好. 在对上证指数波动率的研究中采用3种不同的损失函数，具体表达为：

公式（15）、（16）、（17）分别为平均平方误差MSE、平均绝对误差MAE及拟高斯损失函数QLIKE. 其中表示收益率的平方和；表示不同模型对波动率的预测值；n为样本外预测值的个数.

值得注意的是，在特定的样本下用某一损失函数来评价模型预测能力的结果并不能运用到类似样本中. 为了解决这一问题，Hansen和Lunde［16］提出了“高级预测能力检验法”（Superior Predictive Ability，SPA），但SPA 检验法需要选择基准模型，Hansen 和Lunde［17］随后又提出的模型信度集合（Model Confidence Set，MCS）检验法的模型避免了选择基准模型的问题. MCS检验是剔除所有模型中预测能力较差的模型，直到在显著性水平α下不再拒绝原假设：两个模型的预测能力相同，最后得到的模型就是在1-α的置信水平下的最优模型集合. 选取MSE、MAE 和QLIKE 作为损失函数，使用范围统计量（Range Statistic）和半二次方统计量（Semi-quadratic Statistic），定义如下：

表5 为MCS 检验结果，由在各损失函数下统计量TR和TSQ统计量相对应的概率p值可以看出LSTRGARCH-MIDAS-X 模型概率p值均为1 并且大于GARCH-MIDAS-X 模型和GARCH-MIDAS 模型相对应的概率p值，说明在3个模型中非线性模型LSTR-GARCH-MIDAS-X 对上证指数波动率的预测能力明显要好于另外2个模型.

表5 MCS检验Tab.5 MCS tests

4 结论

本文尝试使用宏观变量WUI研究全球经济政策等不确定性因素对上证指数波动率的影响，在GARCHMIDAS模型的基础上进一步考虑宏观变量WUI对上证指数波动率的非线性影响，结合非线性STR模型提出新的模型LSTR-GARCH-MIDAS-X，并将模型应用到上证指数波动率预测的实证研究中，在参数基本显著的情况下可知，LSTR-GARCH-MIDAS-X 模型不仅在样本内能够很好地拟合上证指数波动率，也证实了全球经济政策不确定性因素对上证指数波动存在非线性影响. 最后通过对模型预测结果进行MCS检验可知：非线性模型LSTR-GARCH-MIDAS-X对上证指数波动率预测的能力优于标准的GARCH-MIDAS模型，表明在预测上证指数波动率时，考虑宏观变量对波动率非线性的影响可以提高对波动率的预测精度.