多物质ALE方法在海啸波冲击方柱问题中的研究

翟 秋 ，张书剑，王华坤，张稼昊，严思寒

(河海大学 港口海岸与近海工程学院，南京210098)

海啸是一种破坏性极强的自然灾害。一些海啸灾害调查报告[1-2]显示，海啸袭击后受灾地区建筑物的损害程度差异较大，保存完好的建筑物往往位于大型建筑物的正陆侧，损坏严重的建筑物通常位于街道的尽头。以上两种现象被称为屏蔽效应和聚焦效应，它们在滨海城市规划、海啸防灾减灾等方面有重要启示作用。

目前大部分物理模型试验侧重于海啸波与单个桩柱或墙体构件相互作用研究，只有少量工作涉及桩柱群和复杂建筑物的海啸波水力特性分析。Hayatdavoodi等[3]对比研究了平板与 T梁在海啸作用下的受力，探讨了水深、波高、淹没深度和抬高高度变化对波浪力的影响，发现平板上的受力一般是线性分布；杨万理等[4]研究了门窗及屋面板洞口对低矮房屋海啸作用力的影响，发现开洞率越大海啸水平力越小；荀东亮等[5]研究了整流板、带切缝的整流板和带空气孔的整流板等3种抗海啸措施，结果表明整流板和带切缝的整流板能减小海啸水平力，带空气孔的整流板能有效减小竖向力；陈橙[6]通过模型实验考察了溃坝波对由平板-桩-斜坡组成的简易高桩码头的冲击过程，分析了面板压强随海啸波高和斜坡角度等因素的变化规律。

由于模型实验成本较高，学者们更多用数值模拟手段来开展研究工作。景旭斌等[7]采用 ALE方法，分析了漂浮物在海啸作用下对陆上建筑的作用力，发现漂浮物的质量、撞击速度对作用力起决定性作用，而被撞建筑的刚度对作用力的影响并不大；杨志莹等[8]用数值模拟的方法，分析了海啸和飓风作用下波高及淹没系数对桥梁中T梁、箱梁受力的影响，发现相比于飓风波，海啸对桥梁主梁的作用力更大，对桥梁安全性威胁更大。Pringgana[9]采用SPH方法研究了方柱自身旋转角度对屏蔽效应及聚焦效应的影响，发现方柱正对海啸波时受到的波浪力最大；Yang等[10]利用ANSYS Fluent软件，研究了溃坝波冲击下前屋对后屋的防护作用，发现如果前后屋之间的间隙足够大，则前屋对后屋几乎没有防护作用；Wei等[11]用GPUSPH的方法，研究了海啸冲击下副公路桥及防波堤对主桥的冲击减缓作用，发现防波堤与主桥之间的最佳减缓距离约为当地水深的8倍或来袭海啸高度的13倍。

海啸波与结构物相互作用数值模拟涉及到流固耦合和自由液面问题，应用较多的有SPH方法[9，11]和VOF方法[12-13]等。然而，SPH方法有着计算量大、耗费机时、自由表面计算精度较低、张力不稳定等问题[14]；VOF方法根据体积比函数F来构造和追踪自由面，在处理F的变化时稍显繁琐[15]。相较而言，多物质ALE法在流固耦合及自由液面问题上具有计算效率高、稳定性好等优势。景旭斌[16]曾采用多物质ALE法对孤立波夹杂漂浮物撞击防波堤的过程进行了数值模拟，体现出该方法在流体冲击问题中的适用性，然而其在沿海结构物海啸防灾减灾方面的应用较少。

本文基于多物质ALE方法建立了海啸波与结构物相互作用数值模型，研究了海啸波对不同结构布置形式下方柱的冲击问题，以探明海啸灾害中的聚焦效应及屏蔽效应。

1 数值模型的构建

流体运动及自由液面的处理采用多物质ALE方法，而在固体域离散时使用拉格朗日描述，固体运动由线弹性结构动力方程或刚体运动方程来控制，流体与固体之间的耦合采用罚函数法，基于上述算法构建海啸波与结构物相互作用数值模型。

1.1 ALE描述流体运动控制方程

流体运动Navier-Stokes方程和连续方程的ALE形式可表述如下

(1)

(2)

式中：ξ为ALE坐标，xi和xj为空间坐标，t为时间，ρ为流体密度，vi为流体速度，ci是流体质点相对于网格点的对流速度，σij为流体应力张量，可用应力偏量和压力来表示

(3)

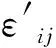
1.2 ALE多物质材料模型

在多物质ALE算法中，不同的材料能在计算区域的网格中自由流动，一个网格可以存在两种及以上的材料，在计算过程中跟踪每种材料的边界，并在相应的单元中进行物质交换及输送，在处理多相流与结构之间相互作用的问题上表现较好。本文涉及水体及空气两种流体材料，水的状态方程采用 Gruneisen方程

(4)

式中：p为压力；E为单位体积内能；C为us-up曲线截距；μ为体积变化率；S1，S2和S3为us-up曲线斜率系数；γ0为Gruneisen系数；α为对γ0的一阶体积修正系数。

空气的状态方程则采用线性多项式状态方程

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E0

(5)

式中：E0为初始比内能，C0～C6为自定义常数。相关参数均可参考景旭斌[7]。

1.3 流固耦合处理方法

采用罚函数法处理流体与固体之间的耦合接触。流体与结构体相互接触时，设流体为主面，结构体为从面。每一个时步先检查各从节点是否穿透主表面，没有穿透则不对该从节点做任何处理；如果穿透，在该从节点与主表面间、主节点与从表面间引入大小与穿透深度和接触刚度成正比的截面接触力，其物理意义相当于在其中放置一系列限制穿透的法向弹簧。

2 数值模型的验证

2.1 溃坝波冲击弹性板算例

根据Rafiee和Thiagarajan[17]提供的算例建立数值水槽，如图1所示。整个水槽由蓄水体、空气域、壁面三部分构成，在空气域中放置一弹性板，其底端固定在床面。弹性板采用拉格朗日单元，材料为线弹性模型；蓄水体及空气域采用多物质ALE单元；水槽壁面按滑移边界处理；对整个系统施加重力。

具体参数如下：蓄水体长L取14.6 cm，高2L，整个水槽长4L；弹性板与水体相距L，厚b取1.2 cm，高20/3b，密度ρ为2 500 kg/m3，杨氏模量E为106N/m2，重力加速度g取9.8 m/s2。当水体右侧闸门被迅速抽离之后，生成溃坝波冲击弹性板。

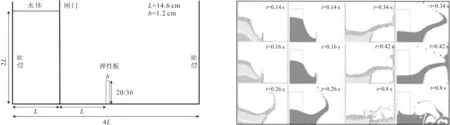
图1 溃坝波冲击弹性板数值模型 图2 溃坝波冲击弹性板的SPH与多物质ALE法结果对比Fig.1 Numerical model of elastic plate impacted by dam break Fig.2 Comparison of SPH and multi-material ALE simulation for breaking dam on elastic plate

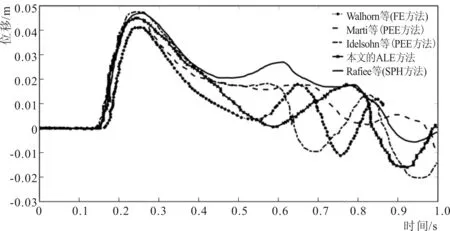
图3 弹性板自由端位移历时曲线比较Fig.3 Comparison between time histories of displacement of the free end of the elastic plate

图2给出了溃坝波自由液面的历时变化。图左为文献[17]SPH结果，右为本文结果，可见两者的溃坝波液面形态吻合很好。将弹性板自由端的位移历时曲线与文献[17-20]结果进行比较，见图3。可以看出，不同方法得到的位移在0.25 s达到最大值，之后振动相位互有偏差，但大体趋势基本一致，即在振动幅值逐渐衰减波动。与各文献数据相比，本文结果处于合理的范围内，证明了本文数值模型的可靠性。

2.2 溃坝波冲击立柱算例

利用Gomez-Gesteira等[21]和Crespo等[22]提供的模型实验数据进一步验证本文算法，建立的水槽模型如图4所示。数值水槽构建方法同上一小节，闸门左侧蓄水体高30 cm，右侧床面以上设置高1 cm的浅水层，在空气域中放置一刚性方柱，高75 cm，底端全约束。

溃坝波冲击方柱的自由液面演变如图5所示。图6比较了柱体所受的溃坝波冲击力。可以看出，本文数值结果与实验数据接近，柱体所受冲击力计算值为34 N，实验结果为32.5 N。但在数值模拟中溃坝波冲击柱体时刻比实验中提前约0.07 s。这是因为本数值模型将水槽底面作滑移边界处理，而实验中存在底床摩擦，虽在闸门右侧区域设置了浅薄水层以减轻水槽摩阻的影响，但无法将其完全消除，实验中摩擦的存在消耗了部分溃坝水体动能，从而导致溃坝波冲击立柱时刻稍晚于数值模拟，且峰值冲击力也略有降低。总体上来看，基于多物质ALE方法构建的数值模型能较为准确地模拟结构物受到的溃坝波冲击力。

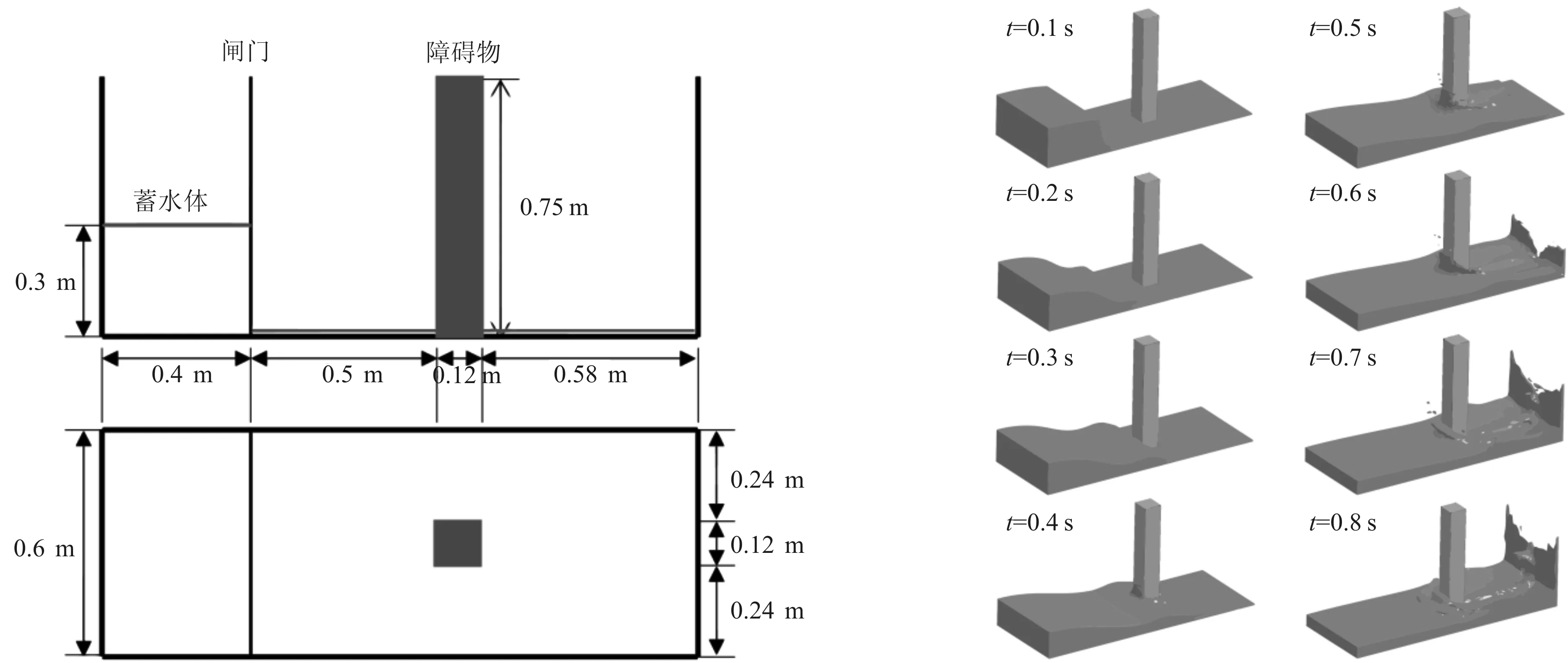
图4 溃坝波冲击刚体柱数值模型 图5 溃坝波冲击刚体柱的各时刻状态Fig. 4 Numerical model of rigid cylinder impacted by breaking dam Fig.5 Time evolution of dam break wave impacting a rigid cylinder

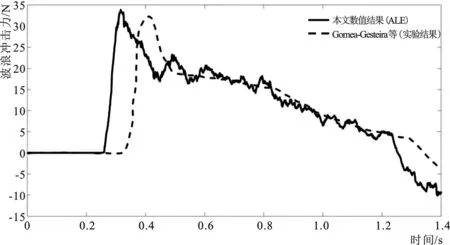
图6 溃坝波冲击力数值模拟与实验数据对比Fig.6 Comparison between numerical and experimental results of tsunami impact force

3 海啸波冲击不同排列下的多柱体研究

3.1 双柱顺排布置

采用多物质ALE法对海啸波冲击双柱顺排布置下的刚性方柱进行探究，数值模型如图7所示。以溃坝波来模拟海啸波，前柱(方柱1)距溃坝水体保持0.5 m不变。后柱(方柱2)与后水槽壁保持0.56 m的距离不变，后柱与前柱之间的距离L分别取0.2 m、0.5 m、0.8 m、1 m四种工况，即无量纲间距比L/d(d为方柱边长)分别为1.67、4.17、6.67、8.33。工况1～4及工况5(单柱)如图8所示。

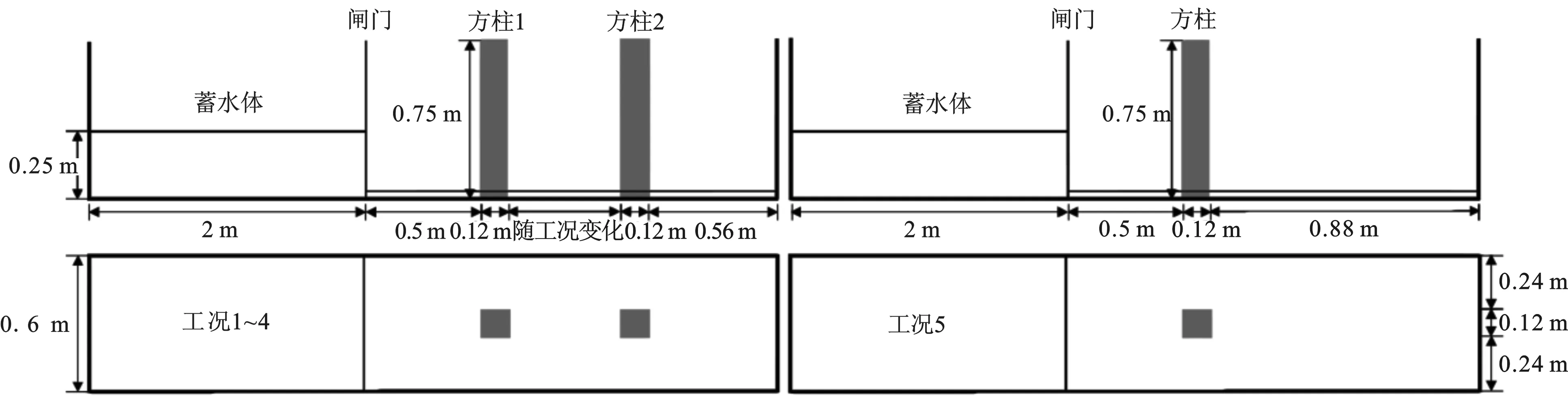
图7 双柱顺排布置数值模型Fig.7 Numerical model for two cylinders in tandem arrangement

方柱1受到的海啸波冲击力如图8所示，五种工况下的冲击力几乎相同，最大值均为24 N左右。各工况下的海啸波冲击力历时曲线差别不大，这表明方柱1受后柱影响很小。

方柱2和单柱受到的波浪冲击力如图9所示，四种工况下方柱2受到的波浪冲击力最大值分别为10.5 N、21.8 N、24 N、24 N；单柱受到的最大冲击力为25 N。工况1下的最大冲击力比其它工况下的减小了50%以上，当L/d由1.67增加到4.17时，最大冲击力由单柱的42%上升到单柱的87%；当L/d继续增加到6.67时，最大冲击力与单柱的最大冲击力25 N几乎相同，即屏蔽效应在L/d为6.67时基本消失。

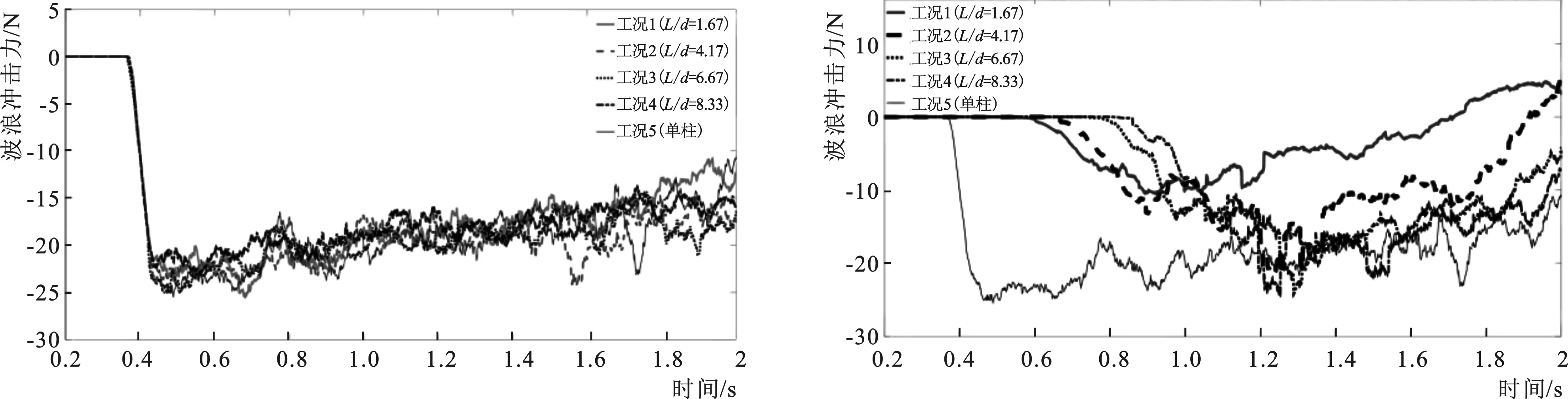
图8 方柱1受到的冲击力 图9 方柱2受到的冲击力Fig.8 Impact force on cylinder 1 Fig.9 Impact force on cylinder 2

不同工况下方柱2受力最大时刻水体自由表面形态如图10所示。在工况1及工况2中，因受到方柱1的屏蔽作用，水体绕过方柱1向后传播，前后柱之间有一明显的低洼水域，冲击在方柱2上的水体动量比方柱1要小。在工况4中，冲击在方柱2上的水体动量与单柱相比几乎相同，前后柱之间观察不到明显的低洼区域。

10-a 单柱10-b 工况110-c 工况210-d 工况4图10 不同工况下方柱2受力最大时刻水体自由表面形态Fig.10 Free surface of water corresponding to the maximum force on cylinder 2

可见，在双柱顺排布置的形式下，两柱的间距越小，前面方柱1的屏蔽作用越明显，方柱2受到的最大冲击力明显减小；当两柱的间距超过一定范围后，将不再产生屏蔽效应。这种现象是因为海啸波冲击方柱1后受到阻碍，在其后方一定区域内形成遮蔽区域，此区域内波速、波高都显著减小；在远离方柱1一定距离之后波浪能量有所恢复，此时前后两柱受到的最大冲击力几乎相同。

3.2 三柱错排布置

对海啸波冲击三柱错排布置下的方柱结构物进行探究，数值模型如图11所示。工况1只设置1根方柱，工况2、工况3、工况4均设置3根方柱，方柱的底面中心点连接起来为一个正三角形，边长L分别为0.5 m、0.7 m、0.9 m，即L/d分别为2.5、3.5、4.5。对各工况下方柱1和方柱3受到的海啸波冲击力进行分析，由于方柱1和方柱2对称布置，此处不再给出方柱2的受力结果。

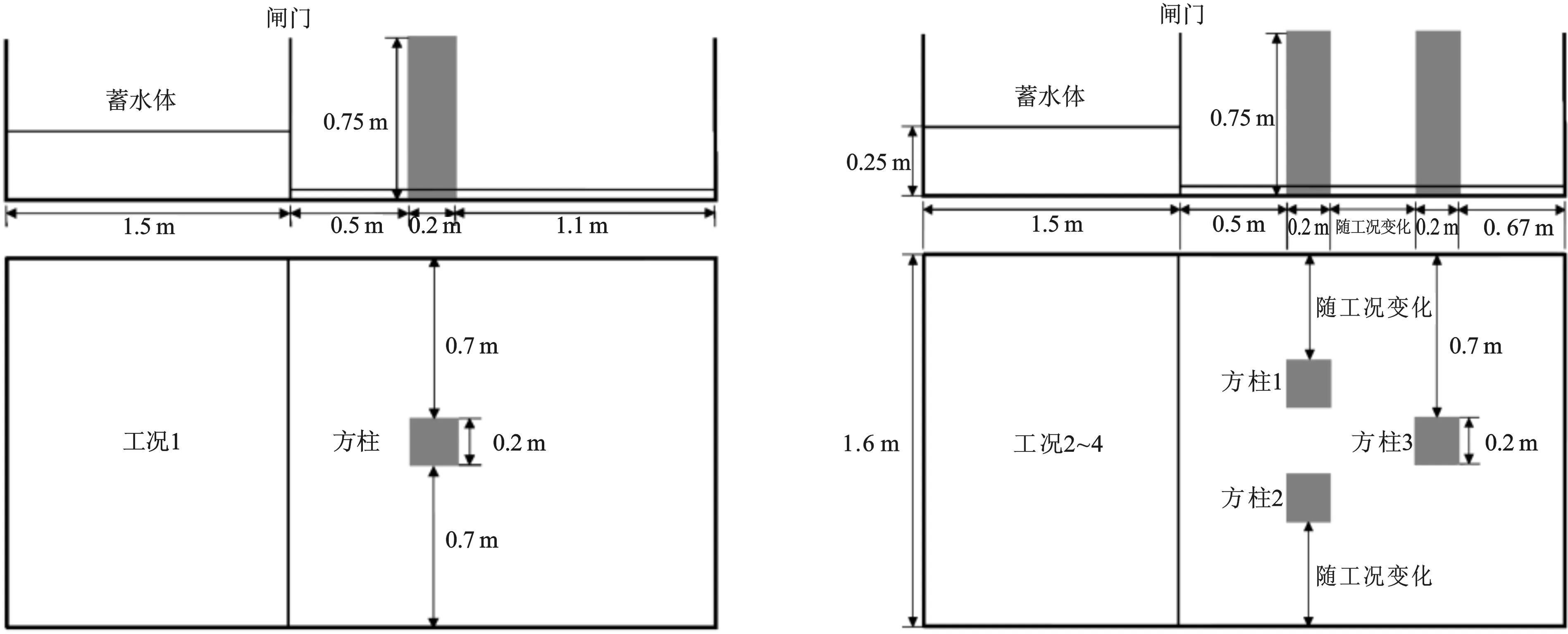
图11 三柱错排布置数值模型Fig.11 Numerical model for three cylinders in staggered arrangement

工况1～4下方柱1受到的冲击力如图12所示。可见，各工况峰值冲击力基本相同，均在106 N左右，各冲击力历时曲线也非常接近。工况2～4的结果显示，随着L/d的增加，方柱1的受力变化较小，这说明方柱1受到的最大冲击力受周围柱体干扰很小。

四种工况下方柱3受到的冲击力如图13所示，冲击力最大值分别为106 N、112 N、120 N、106 N。工况2和工况3中方柱3的冲击力最大值比单柱分别增大了5.6%和13.2%，工况4中方柱3的冲击力最大值与单柱相近。基本规律是：随着L/d的增加，方柱3的受力先增大再减小，最后和单柱接近。当L/d在一定范围内时，方柱1、2的存在会使方柱3受到的峰值冲击力增大。这是因为水流在方柱1、2之间形成很强的间隙流，导致冲击方柱3的水体动量增加。当L/d超过一定值时，间隙流逐渐消失，方柱3的受力接近单柱。

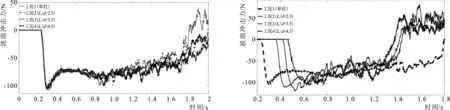
图12 方柱1受到的冲击力 图13 方柱3受到的冲击力Fig.12 Impact force on cylinder 1 Fig.13 Impact force on cylinder 3

不同工况下方柱3受力最大时刻溃坝波态如图14所示。在工况2和工况3下，能观察到方柱1、2之间较强的间隙流，但在工况4下方柱1、2间隙较大，水流的聚集效果已不明显。

14-a 工况114-b 工况214-c 工况314-d 工况4图14 不同工况下方柱3受力最大时刻水体自由表面形态Fig.14 Free surface of water corresponding to the maximum force on cylinder 3

4 结论

本文基于多物质ALE法，综合考虑了空气、水体与结构的耦合作用，对海啸波冲击弹性板及刚体柱两个经典算例进行了验证，证明了该方法不仅能够很好地模拟自由液面，而且能准确地计算水流冲击力和结构动力响应。在此基础上，应用该方法探究了海啸波对双柱顺排布置及三柱错排布置形式下方柱的冲击力规律。结果表明，前柱受力与结构布置形式无关，当L/d较小时(L/d=1.67)，双柱顺排布置形式下后柱受到的波浪冲击力相比单柱能降低50%以上，随着L/d增大，后柱受力逐渐增大，且最终接近于单柱受到的冲击力(L/d≥6.67)，此时意味着屏蔽效应基本消失；三柱错排布置形式下后柱受到的波浪冲击力相比单柱会增大，且随着L/d的增加呈现先增大再减小的趋势，其受力相比单柱最多可增长10%以上(L/d=3.5)，此时聚焦效应显著。因此，滨海城市规划及海工建筑物设计均应考虑结构物的布置形式，尽量利用顺排布置下前方建筑物的遮挡效应，避免错排布置下聚焦水流的冲击，以使海啸灾害减到最小。