大规模MIMO系统中范数双向选择算法
苏 佳,夏 雨
(河北科技大学 信息科学与工程学院,河北 石家庄 050018)
0 引 言
多输入多输出系统在发射和接收端布设了大量的天线,信号主要通过天线集构成的信道矩阵进行传送和接收,这种布设大量天线的方法使得通信系统性能有所提高[1,2]。随着天线数的增加,系统的信道自由度也会随之上升,进而提高信号传输的可靠性[3]。在实际生活中,用户和基站数量的极速增加,给传统MIMO技术带来了巨大挑战,传统MIMO技术已经无法满足人们对信息获取的需求,因此在传统MIMO系统的基础上延伸出了大规模MIMO系统[4,5]。
Massive MIMO系统通过在基站侧布置大量天线单元得到集中式天线系统(co-located antenna system,CAS)。作为第5代(5G)无线系统的核心技术之一,Massive MIMO系统因具有高频谱利用效率和能量利用效率而获得了研究人员的关注,能够在不消耗更多频谱资源的前提下对信道容量和系统能效进行优化。通过国内外的进一步研究,Massive MIMO技术有可能满足未来高速铁路的通信需求,并有潜力产生巨大的经济效益和环境影响,进而促使绿色通信的实现。虽然天线数目的增多可以大幅度提升Massive MIMO系统性能,但在实际部署的过程中需要为每一根天线配备与之对应的射频链路,硬件成本和复杂度也会随之增加,会产生更多系统功耗和硬件损耗[6]。天线选择技术的核心思想就是根据不同的算法,在保证系统性能的前提下,在发射端或接收端选取出最适合当前通信环境传输的天线子集,这些天线子集能够满足信号传输需求,进而降低功耗和损耗。
信道容量与系统能效是优化天线选择算法的两个主要目标。传统天线选择算法中能使容量最优的算法是穷举天线选择法,该算法能够遍历所有可能的天线组合,从而选择出最优的天线子集,虽然这种算法可以使得系统容量最大化,但其运算过程复杂在实际中不可能实现,因此研究人员对天线选择算法进行了研究和改进[7]。文献[8]提到了一种递减天线快速选择算法,天线子集从全集开始逐渐减少,所以这种算法适用于选择天线数量较多的情况;文献[9]结合贪心算法,提出了一种从空集递增选择的算法,逐渐将符合准则的天线加入到空集中,这种算法适合应用在选择天线数较少的通信环境;文献[10]提到了一种范数选择算法,该方法通过计算信道矩阵的范数来对天线进行选择;文献[11]提出了基于机器学习多级分类思想的天线选择算法。
上述几种天线选择算法以损失部分性能为代价,极大程度减少了算法复杂度,不同的算法在不同的通信环境中拥有各自的优缺点。在Massive MIMO系统中,适用于传统MIMO系统的天线选择算法仍具有较高的复杂度,因此研究人员针对Massive MIMO系统中的选择算法进行了研究。文献[12]基于最大体积子矩阵的查找方法,提出了一种实时逐根天线循环迭代的天线选择算法,这种算法具有低内存成本和低运算复杂度;文献[13]在Massive MIMO中提出了一种选择算法,该算法结合了两种关键技术:天线选择和波束成型,最优解通过凸函数来求解,能够同时对系统各方面性能进行优化;文献[14]根据能效最大化的原则,提出了功率分配方案来优化算法,提升性能并降低算法复杂度;文献[15]提出了双向搜索天线选择算法,这种算法适用于不同天线选择数的情况;文献[16]提出了一种能够将接收功率最大化的算法,算法的最优解通过将优化函数转化成另一种凸函数来求解;文献[17]提出的算法名为最小条件数,该算法能够使信道容量趋近于穷举法的信道容量。上述几种天线选择算法虽然从各个方面提升系统性能,但在系统中仍具有较高的复杂度。
在Massive MIMO通信系统条件下,天线选择算法主要分为两类:一类算法是以系统性能最优为前提,但复杂度会随天线数的增加而提高;另一类算法的复杂度较低,但不具有良好的系统性能。本文提出了一种综合考虑系统性能和复杂度的天线选择算法,即最大欧式范数双向选择算法,该算法能够在保持较低算法复杂度的同时提升系统容量。
1 系统模型
本文考虑的大规模MIMO系统,其中发射端配备N根天线,接收端配备M根天线,具有平坦的瑞利衰落信道且具有加性高斯白噪声(additive white Gaussian noise,AWGN),系统信号传输模型可表示为
(1)
其中
y(i)=[y1(i),y2(i),…,yM(i)]T
(2)
x(i)=[x1(i),x2(i),…,xN(i)]T
(3)
n(i)=[n1(i),n2(i),…,nM(i)]T
(4)
(5)
式中:y(i) 代表M维从M根接收天线处收集的i个信号采样点;x(i) 代表N维从N根发射天线处收集的i个信号采样点;n(i) 代表零均值高斯噪声矢量;Es是每根接收天线和每个信道使用的平均功率;较强的散射环境和稀疏的天线间距可以使得信道矩阵更加容易满足独立同分布的瑞利衰落的假设。
在进行天线子集选择时,假设在接收端处已知完整信道状态信息(channel state information,CSI),如果在发射端无法获取完整的信道状态信息,则每根发射天线需要获取相同的发射功率,矩阵H对应的系统信道容量可表示成
C(H)=lb det(IN+EsHHH)=
lb det(IM+EsHHH)
(6)
C(H)为信道H对应信道容量; (·)H表示对矩阵做共轭转置处理; det(·) 表示求矩阵的行列式值;IN表示N维的单位矩阵。
图1为Massive MIMO系统天线选择示意图,N为总的发射天线数,从N根发射天线里选择LN根发射天线,M为总的接收天线数,在M根接收天线选择里选择LM根接收天线进行信号的传输,H为信号传输的信道矩阵,在发射端和接收端均配备了与之对应的射频链路。

图1 Massive MIMO系统中的天线选择
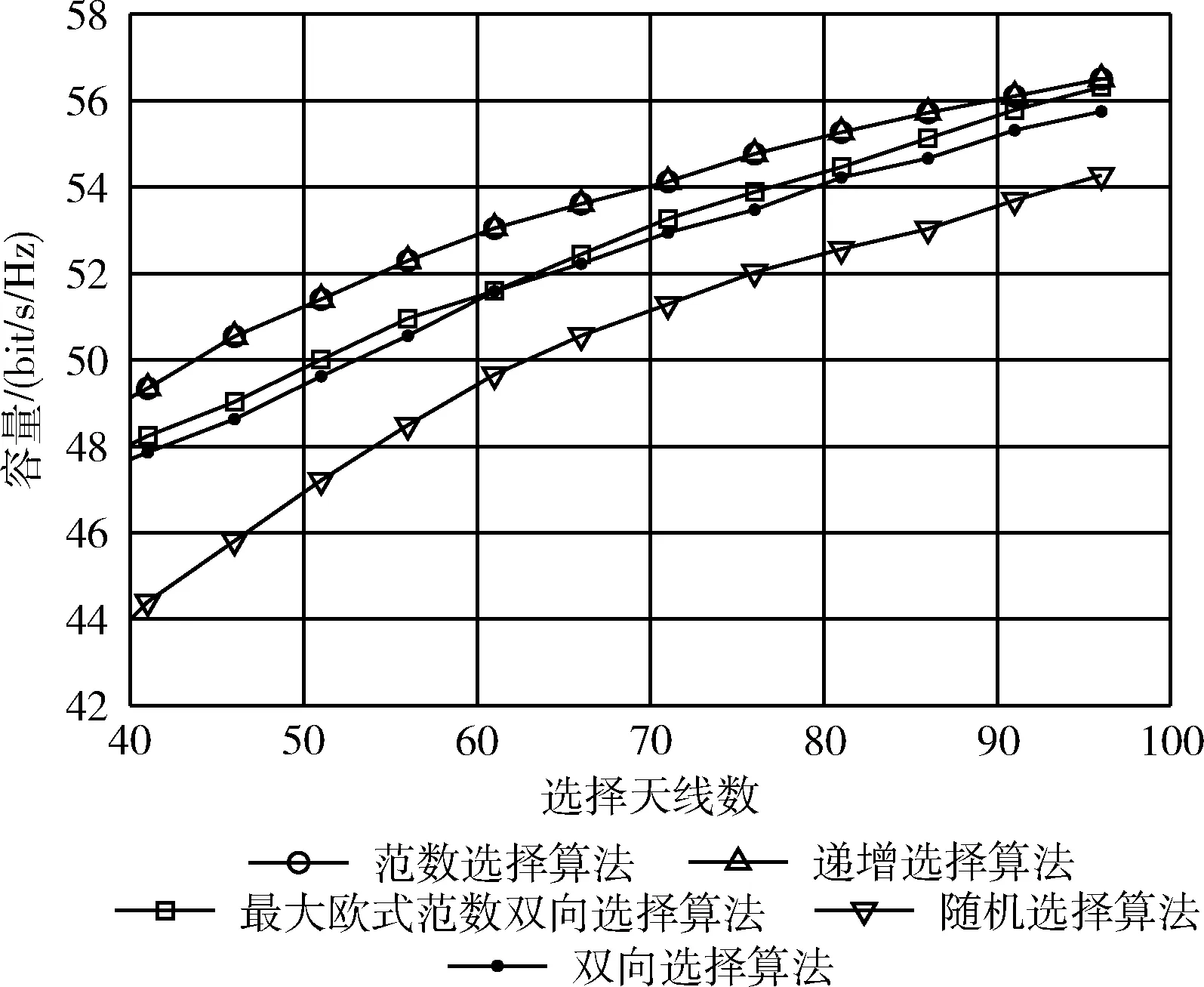
若在发射端选择全部发射天线进行信号发射,即LN=N, 在接收端选择LM根天线来接收信号,LM (7) 大规模MIMO系统的天线选择分为3类: (1)接收天线选择。接收天线选择算法在接收端发挥作用,当接收端已获得完整CSI,在某个约束条件下从所有接收天线中遴选出适合当前通信环境传输的若干根天线来接收信号。 (2)发送天线选择。发射天线选择算法应用在发射端,发射天线选择是在某个约束条件下,从所有发射天线中遴选出适合当前通信环境传输的若干根天线。发射天线对应信道矩阵的列向量,对发射天线进行选择即为通过算法对信道矩阵列向量进行选取。与接收天线选择不同的是,接收端需要将CSI反馈给发送端,发送端将此CSI作为根据来选择天线。 (3)发射与接收天线的联合选择。接收与发射天线的联合选择也叫收发联合天线选择,意思是同时在接收端和发送端进行天线选择。收发联合选择会导致备选天线子集数量成倍增加,极大程度增加了复杂度,因此需要高效的算法来降低复杂度。 天线选择算法中,每根天线对信道容量的贡献度是一个重要指标,不同的天线选择算法对贡献度的计算也不尽相同。例如在范数算法中,通过不同信道子矩阵对应的范数来计算容量贡献度;矩阵体积算法中,通过不同信道子矩阵对应的体积来计算容量贡献度。当天线间存在相关性或者相互影响时,还需要将天线相关行对信道的影响以及天线间影响考虑在内。本文所提算法是通过矩阵范数来计算每根天线的容量贡献度。 双向搜索算法是根据递增算法与递减算法的适用情况来提出的,这两种算法均是通过一系列矩阵知识来简化穷举算法运算的过程。递增天线选择算法选择天线步骤为:算法从空集开始选择,每次将一根对系统容量贡献最大的天线加入到空集中,直到集合中天线符合要求。同理,递减选择算法从待选天线全集开始,每次将一个对系统容量贡献最小的天线去除,直到集合中剩余天线数符合要求。在不同选择天线数的系统环境下,两种算法各有优缺点,递增算法由空天线集合开始逐一增加,适用于选择天线数较少 (LM≤M/2) 的情况;而递减算法从全天线集合中开始逐一减少,适用于选择天线数较多 (LM≥M/2) 的情况。算法具体步骤如下: 算法1: 双向搜索天线选择算法 输入: Λ 输出:Z (1) 初始化Λ,X=Y=∅,B=IN (3)K=argmaxσk, Λ=Λ-K,X=X+K (4)C=(IN+EsH(Λ,∶)HH(Λ,∶))-1 (6) while length(X)≠LM (7) 使用递减选择算法进行天线选择 1)P=argminμk, Λ=Λ-P,Y=X+Λ O(MLM) 2) if length(Y)=LM Z=Y, break end if 4) 对于k∈Λ, 求出每一项σk=σk-|αHhk|2 O(NMLM) (8) 使用递增选择算法进行天线选择 1)K=argmaxσk, Λ=Λ-K,X=X+K 3) 对于k∈Λ, 求出每一项μk=μk+|hke|2 O(NMLM) (9)Z=X (10) end while (11) 返回集合Z 其中,hk(1≤k≤M) 是信道矩阵H中的第k行;Λ为所有接收天线集合;σk(k∈Λ) 为第k根天线对信道容量的贡献,K和P为本次循环选择出天线对应的序号;α、C、e是为简化计算而引入的变量矩阵;算法返回的Z是选择后的天线子集; O(·)H表示最大运算复杂度。 本文通过计算范数来对天线进行选择,提出了最大欧式范数双向选择算法。该算法在循环中同时对两根天线进行选择,直到所选天线子集中的天线数与所需天线数相等,同时处理两根天线的方法加快了选择速度且对系统的容量几乎没有影响。虽然每次循环过程中对两根天线进行了选择,增加了当前循环过程的计算量,但这种方法能够减少下一次每次循环的计算量。 最大欧式范数双向选择算法的主要方法同双向搜索选择算法一样,分别从天线的空集递增,全集递减,当任意集合达到所需天线数即可得到选择后的天线集合。不同的是,在双向搜索算法中,使用的是递增与递减算法来判断天线对容量的贡献度,对天线进行选择,而对于最大欧式范数双向选择算法,在每一次循环中通过计算比较信道矩阵每一行的欧式范数来选择天线,即使用范数选择算法来判断对容量的贡献度。与单纯的使用递增递减算法相比,降低了选择过程中算法的复杂度,这种算法既能在降低算法复杂度的同时减少对系统容量的影响,又能满足不同选择天线数的需求。 算法中对容量贡献的分析主要是通过计算行列式的范数来计算的,以范数选择算法为例,每根接收天线对应信道矩阵的行向量,欧式范数的计算公式为 (8) 算法2: 范数选择算法 输入: Λ 输出:S (1) 初始化,T=Λ O(N2M) (3)n=2 (4) form=1 toM-1 fort=ntoM ifEt>Em temp=Tm O(M2) Tm=Tt Tt=temp end if end for n=n+1 end for (5) forj=1 toLM S=S+Tj O(LM) end for (6) 返回集合S 其中,Λ与T为所有接收天线集合;Ek(1≤k≤M) 表示第k行对应的范数;程序的返回值S为选择后的天线子集。 范数选择算法可使系统具有较高的信道容量,但随着天线数量的增加,算法的计算复杂度也会随之增高。为了降低每一次循环中的计算复杂度,本节提出了最大欧式范数双向选择算法。每一次循环选择天线的过程导致了算法具有高计算复杂度,使用范数选择算法来进行天线选择,进一步降低循环中的计算复杂度。下面总结了最大欧式范数双向选择算法的具体步骤[18]: (1)初始化算法中使用的参数:接收天线集表示为Λ,递增过程选择的天线集表示为X, 递减过程选择的天线集表示为Y,X和Y初始都为空; (2)计算出信道矩阵每个行向量的欧式范数值,从计算出的所有值中选择出值最大的天线K加入到集合X当中,在集合Λ中删除该天线并且在欧式范数值的集合E中删除该天线对应的欧式范数值。从全集开始进行循环递减选择:如果集合X中的元素个数等于LM, 停止天线选择算法;如果集合X中的元素个数不等于LM, 则执行步骤(3)继续进行天线选择; (3)在欧式范数值集合E中选择出值最小的天线P, 在集合Λ中删除该天线同时在欧式范数值的集合E中删除该天线对应的欧式范数值,并且将集合X与集合Λ做并运算并赋值给集合Y。 如果集合Y中的元素个数等于LM, 此时停止天线选择算法并将集合Y赋值给集合Z; 如果集合X中的元素个数不等于LM, 则执行步骤(4)继续进行天线选择; (4)从空集开始对天线进行递增选择,在欧式范数集合E中选择出值最大的天线K加入到集合X当中,在集合Λ中删除该天线同时在欧式范数值的集合E中删除该天线对应的欧式范数值,并且将集合X赋值给集合Z, 返回步骤(3)循环进行天线选择。 (5)将经过算法选择后的天线集合X或Y赋值给集合Z, 结束算法,完成天线选择。 算法3: 最大欧式范数双向选择算法 输入: Λ 输出:Z (1) 初始化Λ,X=Y=∅ O(N2M) (3)K=argmaxEk,E=E-EK, Λ=Λ-K,X=X+K (4) while length(X)≠LM (5) 通过范数比较进行递减选择 1)P=argminEk 2)E=E-EP, Λ=Λ-P,Y=X+Λ 3) if length(Y)=LM Z=Y, break end if (6) 通过范数比较进行递增选择 1)K=arg maxEk O(MLM) 2)E=E-EK, Λ=Λ-K,X=X+K (7)Z=X (8) end while (9) 返回集合Z 其中,hk是信道矩阵H中的第k行;Ek表示第k行对应的欧式范数,K和P为本次循环选择出天线对应的序号;程序的返回值Z为选择后的天线子集。 从算法1和算法2的步骤中可以看出,范数选择算法的复杂度为O(M2), 双向搜索算法的复杂度为O(NMLM), 而从算法3中可以看出最大欧式范数双向选择算法的复杂度为O(MLM), 与双向搜索算法相比有所降低,且选择天线数等于接收天线数时 (LM=M), 最大欧式范数双向选择算法的复杂度与范数选择算法相等,此时情况相当于未进行天线选择。相比于原范数天线选择算法,每一次循环处理的天线数为两根,相当于将原先需要循环的总次数减少了一半,选择出天线所需要得循环总数减少为M/2。 为了分析文中提出的最大欧式范数双向选择算法的性能,本文从系统性能和计算复杂度两个方面与已有算法——递增选择算法、随机选择算法、双向搜索选择算法以及范数算法进行仿真和比较,使用上述算法对接收端天线进行天线子集选择。对Massive MIMO系统的上行链路进行仿真,终端发射端设有N根发射天线,基站接收端设有M根接收天线,信道仿真环境为瑞利平坦衰落信道,信道矩阵中的各个元素为高斯随机变量,服从独立同分布。 在发射天线数N=16, 接收天线数M=128, 选择天线数LM的范围为0~120,系统默认信噪比为10 dB的条件下进行仿真,图2与图3为采用不同算法时容量与选择天线数的关系图,图2选择天线数范围为0~40,图3选择天线数范围为40~100。 图2 容量与选择天线数(0-40)的关系 由图2可以看出,系统容量随着选择天线数量的增加而不断提升,通过比较实验仿真的算法,递增和范数算法对应的系统容量最佳,为容量上界;而随机选择算法对应的系统容量最差,为容量下界。当选择天线数小于40时,最大欧式范数双向选择算法与双向搜索算法的性能比较接近于递增选择算法;天线数大于40时的曲线趋势如图3所示。 图3 容量与选择天线数(40-100)的关系 由图3可知,当选择天线数等于60时,相比于双向选择算法,所提新算法对应的系统容量提高了0.89 bit/s/Hz;当选择天线数在40到100范围内,可明显看出最大欧式范数双向选择算法对应的系统容量较高,但低于范数选择算法对应的系统容量。这是由于使用了双向选择算法从而降低了范数选择算法的复杂度,但会对系统容量造成了一定影响,所以未能达到范数选择算法的系统容量。 在发射天线数N=4, 接收天线数M=100, 系统默认信噪比为10 dB的条件下进行仿真,图4为在固定选择天线数LM=70的前提下,采用不同天线选择算法获得的系统容量与信噪比关系的曲线。 图4 容量与信噪比的关系 由图4可以看出,算法的信道容量曲线随信噪比的提高呈现不断上升的趋势,最大欧式范数双向选择算法的信道容量曲线在其他所有曲线的上方;而随机选择算法的信道容量曲线在其他所有曲线的下方;最大欧式范数双向算法的信道容量曲线位于双向选择算法信道容量曲线的上方,这是因为通过计算欧式范数来判断每根天线对容量贡献权重的方法能够选择出更适合当前通信环境传输的天线,进而提高了信道容量上限值。当信噪比等于10 dB时,与范数选择算法相比较,所提新算法的信道容量值提高了1.6 bit/s/Hz;与双向选择算法相比较,所提新算法的信道容量值提高了2.21 bit/s/Hz。相比于原双向选择算法,所提新算法在不同信噪比的通信环境下具有更优的信道容量值。 在发射天线数N=4, 接收天线数M=100,系统默认信噪比为10 dB的条件下进行仿真,选择天线数LM范围为0~99根。在仿真实验中,不同算法在相同参数的约束下重复执行100次,记录下每一种天线选择算法运算的总时间。 从图5可以得知,欧式范数算法的运行时间随选择天线数量的增加而提高,这是因为随着选择天线数量的增加,在对每根天线对应范数的计算过程中,将范数按照从大到小进行排序所消耗的时间基本呈线性增加,所以算法对应的计算复杂度也会呈线性增加,最大迭代次数为M。 而所提新算法利用了双向搜索选择算法的优点,在每一次循环中处理的天线数量为两根,这相当于减少了一半的计算量。随着选择天线数量的增加,算法的运行时间先增加后减少,在LM=M/2时达到最大值,将迭代次数的最大值从M降低到M/2。 仿真结果表明,相比与范数选择算法,当选择天线数在1至50之间时,最大欧式范数双向选择算法运行时间降低了一半;当选择天线数量等于99根时,与范数选择算法相比较,最大欧式范数双向选择算法的运行时间降低了0.29 s,所以此算法更能满足不同天线选择数的需求。 图5 新算法与范数选择算法复杂度的对比 从图6可以得知,不同天线选择数的需求下,最大欧式范数双向选择算法和双向搜索选择算法均有较好的信道容量,但最大欧式范数双向选择算法的时间曲线位于双向搜索算法之下,即时间复杂度更低,这是因为所提新算法结合了欧式范数选择算法复杂度较低的优点:可选出较优的天线子集,进而降低了算法复杂度。双向搜索算法的时间复杂度为O(NMLM), 而双向选择算法的时间复杂度为O(MLM), 复杂度得到了有效优化。结果表明,当选择天线数等于50根时,相比于原来的双向搜索算法,最大欧式范数双向选择算法的运行时间降低了0.08 s,减少了原算法的复杂度;当选择天线数小于或大于50时,算法的运行时间均有所降低。 图6 新算法与双向搜索算法复杂度的对比 本文针对大规模MIMO系统,提出了最大欧式范数双向选择算法。在每一次循坏迭代中,使用范数选择算法同时选择出对容量贡献最大和最小的两根天线,与原算法相比,算法复杂度得到了极大的改善,并且未损失过多的系统容量。 通过对系统容量进行分析,将最大欧式范数双向选择算法与常用的传统天线选择算法进行比较,仿真结果表明,最大欧式范数双向选择算法对应的系统容量方面得到了改善,有一定的提高,在灵活应对不同选择天线数量需求的时候有更好的表现;通过循环运行不同算法,对算法运行时间进行比较,仿真结果表明,与现有的欧式范数和双向搜索算法相比,文中所提算法减少了算法的运算时间,在一定程度上降低了算法复杂度。2 天线选择算法
2.1 双向搜索算法
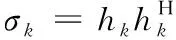
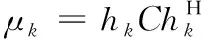
2.2 最大欧式范数双向选择算法
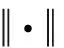


3 仿真结果
3.1 容量与选择天线数的关系

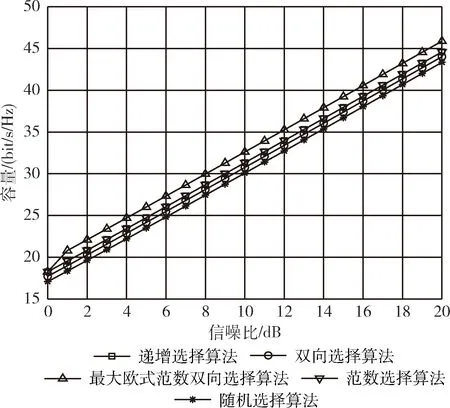
3.2 容量与信噪比的关系
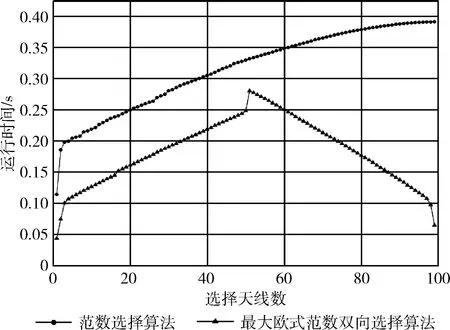
3.3 算法复杂度与选择天线数的关系
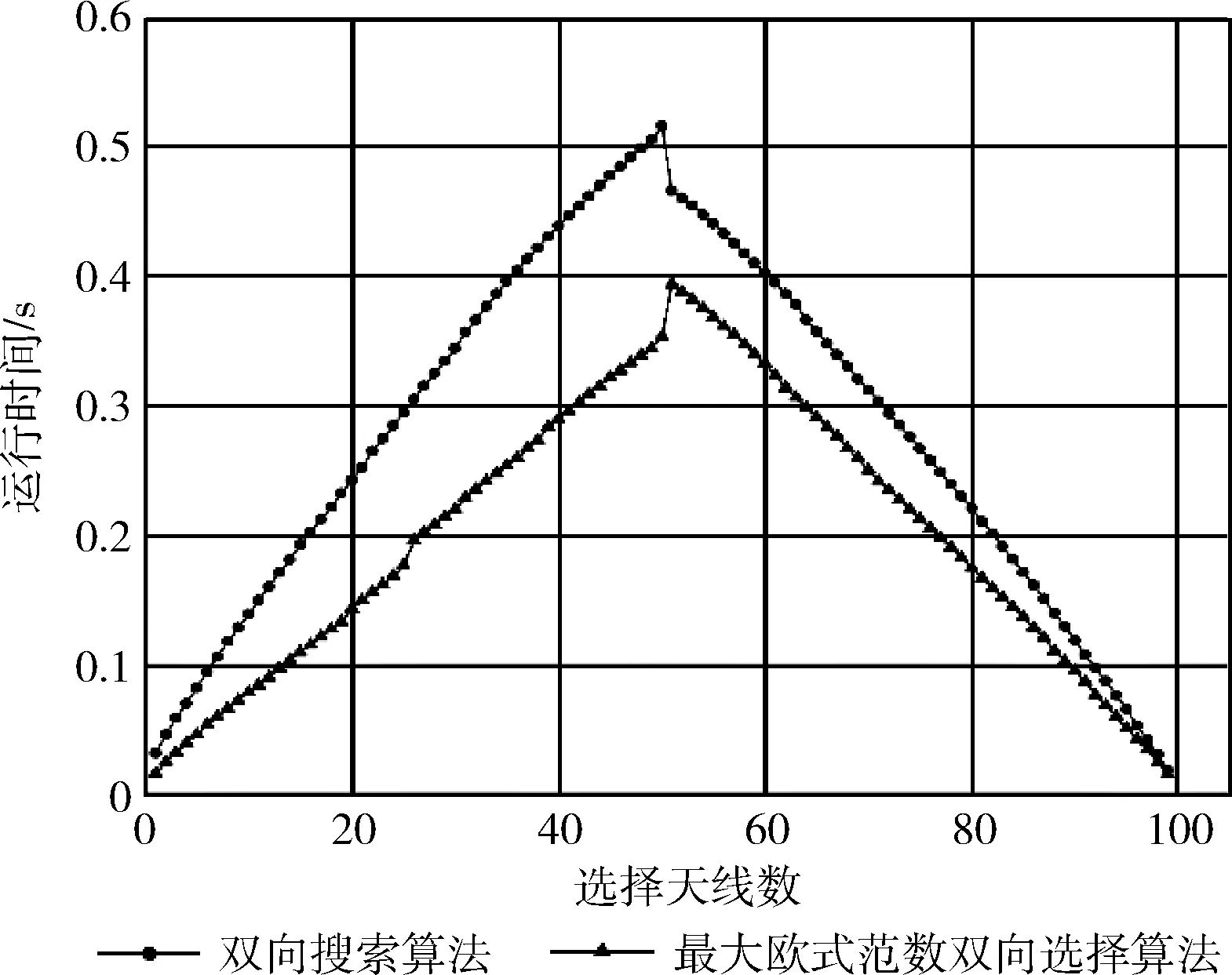
4 结束语

