基于改进狼群算法的概率积分法模型参数反演方法

李靖宇，王 磊，江克贵，滕超群

( 安徽理工大学 测绘学院，安徽 淮南 232001 )

我国能源资源结构具有“富煤、贫油、少气”的特点，其中煤炭资源在一次能源结构的生产和消费中所占比例高达76%和66%，因此在可再生资源形成规模之前，煤炭将长期作为主体能源担负着国家能源安全和经济持续发展的重任[1]。高强度的煤炭开采势必会造成矿区环境灾害问题，如地面塌陷、工程地质损害等，开采沉陷预计对于“三下”采煤、矿区环境灾害防治可起到指导性作用，因而开采沉陷预计一直是我国矿山领域的热点问题。概率积分法是我国普遍采用的开采沉陷预计方法，该方法已积累大量的实践经验，形成了相对成熟的预计参数体系[2]，如何基于实测数据，精确、快速、可靠地获得概率积分法模型参数，一直是该方法应用的难点。

概率积分法模型参数反演主要经历了特征点法、线性近似法[3]、正交实验法[4]，特征点法因曲线特征点难以精确确定进而导致求参误差大；线性近似法对模型参数初值要求极高，若初值精度不高，则会导致求参模型发散；正交实验法求参速度慢且不易借助计算机实施；针对概率积分法模型参数反演中存在的问题，一些专家学者提出采用智能优化算法反演概率积分法模型参数。查剑锋[5]等利用遗传算法进行概率积分法模型参数反演，此后又有专家学者将粒子群算法[6]、人工蜂群算法[7]、果蝇算法[8]引入到了概率积分法模型参数反演中，为概率积分模型参数反演提供了新途径。近年来，吴虎胜[9]等提出了狼群算法，与传统智能优化算法相比，狼群算法具有收敛速度较快、可有效避免局部最优解、统计结果精度较高等良好的寻优特性；文献[10-12]对狼群算法提出了改进方案，进一步提高了狼群算法的寻优特性。目前，狼群算法已在移动机器人路径规划[13]、桥起主梁优化[14]、井下排水采气超声速喷嘴优化[15]等领域得到了广泛应用，但鲜有概率积分法模型参数反演方面的案例报道。

鉴于此，本文在分析狼群算法优缺点的基础上提出二次游走、变异行为改进策略，形成了改进狼群算法( IWPA )，与狼群算法相比，改进狼群算法的搜索精细程度、跳出局部最优解能力得到了有效提高，并将改进狼群算法引入概率积分法模型参数反演中，构建改进狼群算法的概率积分法模型参数反演方法( MIWPA )。

1 反演方法

1.1 基本狼群算法

人工狼群狩猎区域[15]为一个N×D的欧氏空间( N为人工狼总数，D为待求参数维度 )，任意一匹人工狼为Wn＝( wn1，wn2，…，wnd，…，wnD)。在人工狼群中，每一匹人工狼都是随机生成的，随机生成人工狼的公式为

式中，wnd为第n匹人工狼在第d维空间中的位置( 即第n组随机参数中的第d个参数 )；wmax，wmin分别为wnd中的最大值、最小值；rand为-1至1之间均匀分布的随机数。

( 1 ) 头狼产生规则

在人工狼群中，头狼感知气味浓度最大，头狼不断变化且不参与游行、奔袭、围攻行为。

( 2 ) 游走行为

探狼是除头狼外、感知气味浓度较大的人工狼。探狼每次游走向不同方向前进，每次前进后返回原来位置，若探狼前进后感知气味浓度超过头狼感知气味浓度，则更新头狼并进行奔袭行为，若不是，则继续游走直至更新头狼或达到最大游走次数；游走结束后，若探狼感知最大气味浓度大于当前位置感知气味浓度，则更新探狼。第k次前进后，探狼的位置为

式中，wnd为开始搜寻猎物前，探狼在第d维空间中的位置；step ad为探狼在第d维空间中的游走步长。

( 3 ) 奔袭行为

猛狼是距头狼较近的人工狼。猛狼在奔袭过程中，若感知气味浓度超过头狼感知气味浓度，则更新头狼且继续奔袭行为，直至猛狼与头狼之间的距离满足要求。猛狼奔袭后的位置为

式中，wnd为猛狼在第d维空间中的位置；step bd为猛狼在第d维空间中的奔袭步长为头狼在第d维空间中的位置。

( 4 ) 围攻行为

猛狼、探狼接收头狼的信号后，开始围攻猎物，若每次攻击后感知气味浓度超过原位置感知气味浓度，则更新该人工狼。第k+1次攻击后的位置为

( 5 ) 狼群更新规则

围攻结束后，淘汰感知气味浓度较小的人工狼，同时根据式( 1 )，( 2 )随机生成相同数量的人工狼。

1.2 狼群算法改进策略

( 1 ) 二次游走

在狼群算法游走行为中，存在下述问题：首先，对于某一探狼而言，其游走方向数固定不变；其次，当探狼游走至猎物附近时，游走步长可能会超出探狼与头狼间的距离，游走后无法感知更大的气味浓度，此时探狼与猎物间虽具有一定距离，但无法进一步靠近猎物；最后，当探狼与猎物间的初始距离较大时，游走后感知更大的气味浓度并向猎物前进，但游走步长可能略小，直至游走结束，距离猎物仍有一定距离。假如探狼A，B游走方向数为4，则狼群算法游走方式如图1所示。

针对上述问题，为提高狼群算法的搜索精细程度，提出了二次游走改进策略，其思想如下：

① 将狼群算法探狼游走视为一次游走，探狼选择以一次游走感知气味浓度最大的方位为起点，进行二次游走。

图1 WPA探狼游走Fig.1 WPA spies the wolf

② 探狼二次游走时，根据一次游走结果，做出不同的反应：对于探狼A而言，其二次游走与一次游走相比，方向数相同但步长较长；对于探狼B而言，其二次游走与一次游走相比，方向数较多且步长较短。

假如探狼A，B游走方向数为4，则改进狼群算法游走方式如图2所示。

图2 IWPA探狼游走Fig.2 IWPA spies away

③ 探狼二次游走中，每一次前进后，返回二次游走前位置，第m次前进后的位置为

式中，wnd1为探狼一次游走感知气味浓度较大的方位为探狼第d维空间中的二次游走步长。

( 2 ) 变异行为

狼群算法为跳出局部最优解，对狼群进行狼群更新：淘汰部分感知气味浓度较低的人工狼并随机生成等数量的人工狼；但生成的大部分人工狼适应度函数较低或距离头狼较远，无法成为探狼或猛狼，因此没有参与到狼群游走、奔袭、围攻行为中，并在下一次迭代前的狼群更新中被淘汰，从而导致狼群算法跳出局部最优解能力受到限制。针对上述问题，提出变异行为改进策略，其思想如下。

① 召唤行为后，狼群并不立刻进行围攻行为，而是将头狼与其他人工狼按比例混合，如式( 7 )所示。

② 混合后，若人工狼感知的气味浓度变大，则更新其位置。

③ 人工狼更新后，重新选择头狼、探狼、猛狼并进行围攻行为。

1.3 反演方法构建

根据1.2节改进的狼群算法，结合开采沉陷概率积分预计模型，提出了基于改进狼群算法的概率积分法模型参数反演方法，其主要过程如下：

Step 1：地面实测下沉值、水平移动值分别记为Ss，Ms，利用概率积分法模型参数计算的预计下沉值、水平移动值分别记为Sy，My，以实测值与预计值之差平方和最小为准则，构建适应度函数为

式中，Ssi，Msi，Syi，Myi分别为地面观测点( Xi，Yi)对应的Ss，Ms，Sy，My。

Step 2：设置狼群数量N、最大迭代次数Dmax、最大游走次数Tmax等参数；给定概率积分法模型参数中心值B0＝[q0，tan β0，b0，θ0，S10，S20，S30，S40]，各概率积分法模型参数的波动范围ΔB＝[Δq，Δtan β，Δb，Δθ，ΔS1，ΔS2，ΔS3，ΔS4]，生成人工狼群Bi＝[qi，tan βi，bi，θi，S1i，S2i，S3i，S4i]( i＝1，…，N )。

Step 3：以适应度函数值为判断人工狼感知气味浓度Yn大小的依据，适应度函数值越小则人工狼感知气味浓度越大，选择感知气味浓度最大的人工狼为头狼，记其位置、感知气味浓度分别为wlead，Ylead。

Step 4：选择除头狼外、感知气味浓度较大的人工狼为探狼，探狼根据式( 3 )进行一次游走后，根据式( 6 )进行二次游走，直至二次游走后探狼感知气味浓度Yn2＞Ylead或游走次数T＝Tmax后，进行奔袭行为，若Yn2大于一次游走后该探狼感知气味浓度Yn，则更新该探狼。

Step 5：选择距离头狼较近的人工狼为猛狼，猛狼根据式( 4 )向头狼奔袭，若奔袭过程中猛狼感知气味浓度Yn＞Ylead，则更新头狼，继续召唤行为；若Yn＜Ylead，则猛狼继续奔袭，直至猛狼与头狼间距离Dn小于要求距离D。

Step 6：根据式( 7 )，对人工狼进行变异，若变异后感知气味浓度YnB大于变异前感知气味浓度Yn，则更新该人工狼，变异结束后重新选择头狼、探狼、猛狼。

Step 7：根据式( 5 )，探狼联合猛狼对猎物进行围攻。

Step 8：对头狼进行更新，淘汰部分感知气味浓度较小的人工狼，并根据式( 1 )，( 2 )随机生成等数量人工狼。

Step 9：判断是否达到精度要求或最大迭代次数Dmax，若达到，则输出头狼位置，即概率积分法模型参数，否则转至Step 3。

基于改进狼群算法的概率积分法模型参数反演方法( MIWPA )的运行流程如图3所示。

图3 MIWPA流程Fig.3 Flow chart of MIWPA

2 模拟试验

2.1 工作面概况

以淮南矿区地质采矿条件为背景，模拟工作面走向开采长度D3＝800 m，倾向开采长度D1＝300 m，煤层平均采厚m＝3 m，煤层倾角α＝5°，平均采深400 m，采用全部垮落法管理顶板开采。在工作面走向每隔20 m布设1个监测点，共51个监测点；沿工作面倾向每隔20 m布设1个监测点，共36个监测点，模拟工作面如图4所示。矿区概率积分法模型参数为：下沉系数q＝0.8，水平移动系数b＝0.25，主要影响角正切tan β＝2.5，最大下沉角θ＝85°，上、下、左、右拐点偏移距为S1＝S2＝S3＝S4＝60 m。

图4 模拟工作面及地表监测点布置Fig.4 Schematic diagram of simulated working face and surface monitoring points

2.2 改进狼群算法参数估计准确性

分别利用MWPA，MIWPA进行概率积分法模型参数反演，试验设计方案如下：参数q，tan β，b，θ，S1，S2，S3，S4波动范围分别为0.5～1.1，2.0～3.0，0.05～0.45，82～88，40～80，40～80，40～80，40～80，为了防止试验结果出现偶然性，进行10次概率积分法模型参数反演试验，计算参数中误差及参数相对误差，试验结果见表1。

表1 MWPA 和MIWPA 参数估计值与设计值对比Table 1 Estimated values of MWPA and MIWPA parameters were compared with the design values

由表1可知：在参数相对误差方面，MWPA反演参数相对误差最大不超过6.3%，MIWPA反演参数相对误差最大控制在3.4%以内。在参数拟合中误差方面，MIWPA反演参数拟合中误差均小于MWPA，MWPA反演参数中误差最大不超过9.39，MIWPA反演参数中误差最大不超过4.02。

试验结果表明，与MWPA的反演参数结果相比，MIWPA方法更加稳健，且参数反演参数精度大幅提高。

2.3 改进狼群算法的可靠性

为进一步证明MIWPA的可靠性，基于模拟试验，分别利用MWPA和MIWPA反演概率积分模型参数10次，反演参数结果的波动情况如图5所示。由图5可知，与MWPA相比较，MIWPA反演参数波动范围较小，反演参数更接近于真实值。

综上所述，MIWPA反演参数的稳定性、精度均优于MWPA，MIWPA反演概率积分法模型参数具有更好的可靠性。

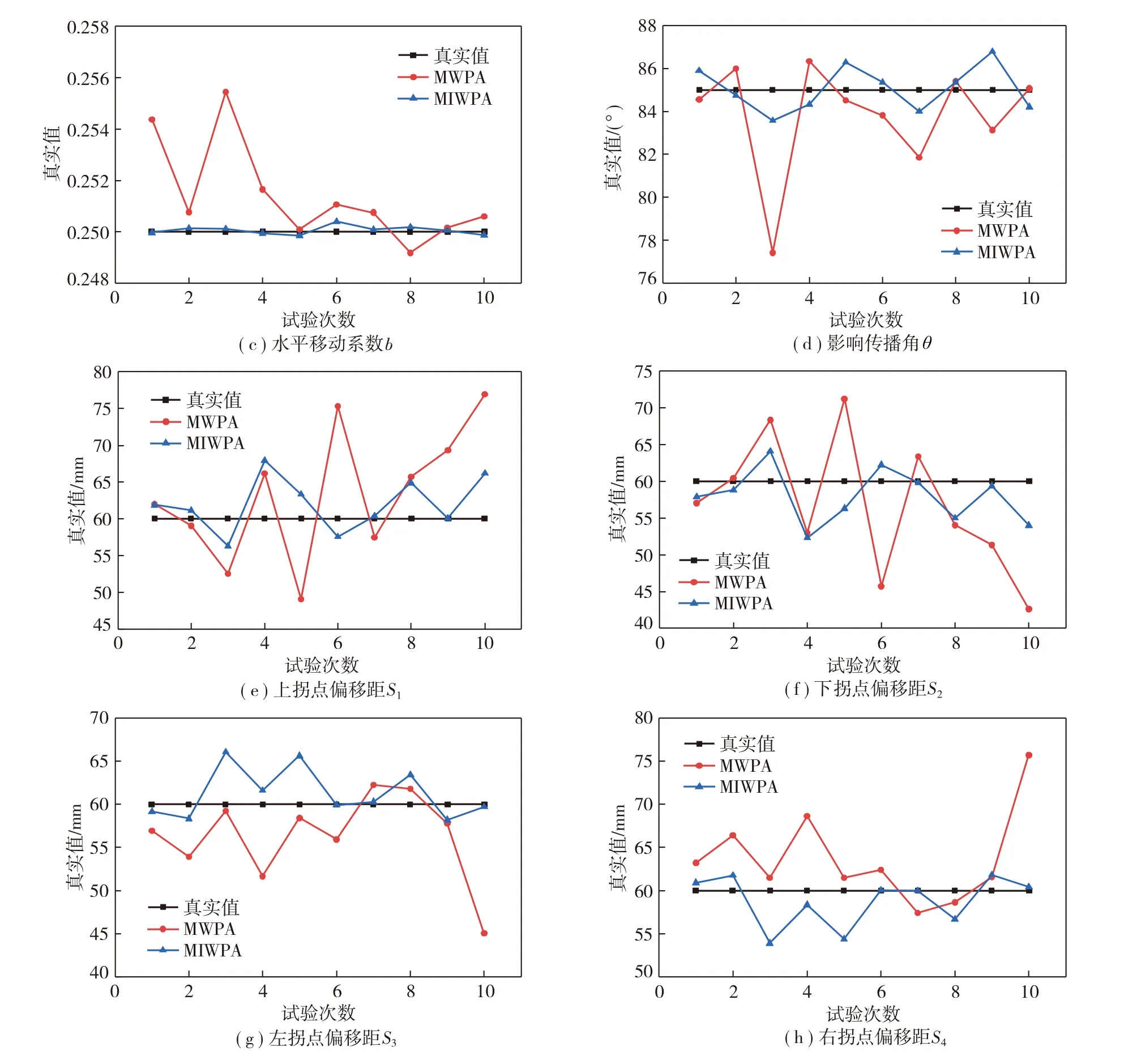
图5 10次模拟试验反演参数波动情况Fig.5 Fluctuation of parameters was inversed in 10 simulation experiments

3 工程实例

3.1 矿区概况

淮南顾桥南矿1414( 1 )为顾桥煤矿南区的第1个回采工作面，工作面从矿床边界开始向巷道往回开采，采用机械化掘进，垮落法管理顶板，一次采全高，工作面地质采矿条件为：走向开采长度2 120 m，倾向开采长度251 m，平均采深735 m，煤层平均采厚3 m，煤层倾角5°。主断面倾向观测线布置在距开切眼约1 144 m、终采线约976 m处，倾向线长度为1 500 m，相邻点之间点间距为30 m，共布设3个控制点和50个监测点。主断面走向观测线布置在下山方向偏离工作面中心线39 m的方向上，走向线长度约3 480 m，相邻点之间点间距为30 m/60 m，共布设3个控制点和95个监测点。观测站布设如图6所示。

图6 观测站布设Fig.6 Observation station layout

3.2 试验结果及分析

将顾桥南矿1414( 1 )的实测数据经过预处理，在走向线上选取75个监测点，在倾向线上选取47个监测点，利用MWPA，MIWPA进行概率积分法模型参数反演。为避免试验的偶然性，进行了10次试验，然后分别计算参数平均值与参数中误差。其结果见表2。

表2 MWPA 和MIWPA 在工程应用中求参结果比较Table 2 Comparison of parameter calculation results between MWPA and MIWPA in engineering application

由表2可知：从参数中误差方面来看，MIWPA反演参数q，tan β，b，θ中误差控制在0.88以内，拐点偏移距S1，S2，S3，S4中误差最大不超过4.65，MWPA反演参数q，tan β，b，θ的中误差控制在1.08以内，拐点偏移距S1，S2，S3，S4中误差最大不超过5.34；表明MIWPA稳定性优于MWPA。利用MIWPA反演顾桥矿1414( 1 )工作面概率积分法模型参数为：q＝0.93，tan β＝1.98，b＝0.42，θ＝84.53°，S1＝-12.44 m，S2＝-18.80 m，S3＝55.06 m，S4＝33.98 m。

将MIWPA反演的概率积分法模型参数代入概率积分法模型，计算出的下沉曲线、水平移动曲线分别如图7，8所示。

图7 MIWPA工程实例参数估计下沉值拟合情况Fig.7 Parameter estimation subsidence value fitting of MIWPA project example

图8 MIWPA工程实例参数估计水平移动值拟合情况Fig.8 Fitting condition of parameter estimation horizontal moving value of MIWPA project example

由图7，8可知，下沉值、水平移动值的实测曲线与拟合曲线基本一致，实测值与拟合值间的绝对值误差均不超过300 mm，下沉与水平移动拟合中误差为114.88 mm。可见，MIWPA在反演概率积分法模型参数中具有实际应用价值。

4 结 论

( 1 ) 在分析WPA优缺点的基础上，提出二次游走、改进变异行为策略，形成了改进的WPA( IWPA )，并将IWPA引入概率积分法模型参数反演中，构建了基于改进狼群算法的概率积分法模型参数反演方法( MIWPA )，并编制了工程应用程序。

( 2 ) 通过模拟试验论证了MIWPA的精确性与可靠性。模拟试验结果表明：MIWPA反演参数相对误差、参数中误差分别不超过3.4%，4.02，满足工程要求；MIWPA的准确性、可靠性均优于MWPA。

( 3 ) 利用MIWPA对顾桥矿1414( 1 )工作面概率积分法模型参数反演。概率积分法模型参数结果为q ＝0.93，tan β ＝1.98，b ＝0.42，θ ＝84.53°，S1＝-12.44 m，S2＝-18.80 m，S3＝55.06 m，S4＝33.98 m，下沉值与水平移动值拟合中误差为114.88 mm。