水下爆炸冲击下码头结构动力响应的数值模拟

赵利平,张 锋，彭 雄，郭锦泽

(1.长沙理工大学水利工程学院，长沙 410114；2.水沙科学与水灾害防治湖南省重点实验室，长沙 410114)

水下爆炸作为工程中常用的一种爆破手段，广泛运用于港坞建设、航道疏浚、河道开挖、桥墩拆除等工程中。码头结构作为港口工程最常见的结构形式，一方面容易受到爆炸冲击，造成不利影响；另一方面，对于老旧的结构，也可以用水下爆炸的方式拆除。因此，对水下爆炸冲击荷载作用下高桩码头的毁伤效应进行研究，剖析水下爆炸冲击荷载对高桩码头的动力响应特性及损伤规律，探寻该类结构在爆炸荷载作用下的薄弱处，对提高高桩码头的抗爆防护性能及有效拆除具有重要意义。

水下爆炸领域的探索经历了漫长的过程。在理论研究方面，盖京波等[1]通过守恒定律以及算例分析，得到了冲击荷载下多层结构中的透射波强度解析式。刘文华等[2]从灰色系统理论出发，揭露了水下爆破的参数与效果之间的关系。李澎等[3]用多种方程组成的方程组，近似计算了冲击波峰值，并与实测数据进行对比，相似率结果一致。陆遐龄等[4]通过水下爆炸相似规律及实际监测对比，给出了爆炸相似准则。Ritwik等[5]以结构响应中的反射系数为研究点，探究了各种参数对反射系数的影响。在试验方面，胡晶等[6]利用离心模型试验对比了水下爆炸和空爆产生的荷载对结构的损伤。黄晓明等[7]利用爆炸筒试验及高速摄影记录，分析了箱梁模型中垂破坏的原因。刘靖晗等[8]通过对高桩码头进行水下爆炸试验，分析了不同位置下的破坏模式和毁伤机理。由于模型试验成本巨大，且条件苛刻，因此相关学者采用数值仿真软件对水下结构开展研究。Zhang等[9]通过SPH模型，分析了水下爆炸冲击载荷对钢性板的损伤。赵小华等[10]通过建立数值耦合模型，找到了混凝土重力坝结构的薄弱处。张社荣等[11-12]基于水和空气的不同介质属性，对比分析了两种介质下冲击波的传播规律，并结合得出的结论，进一步分析了不同介质下混凝土重力坝的动态响应。Zhao等[13]通过建立数值模型，比较了钢筋混凝土板在空气和水下接触爆炸作用下的损伤特性。由于水下爆炸结构方面的研究多以单桩构件为主，对整体结构的研究偏少，而爆炸冲击波产生的流场扰动会直接作用在水下结构上，对结构产生损伤，对单桩构件的研究难以反映出整体结构在水下爆炸荷载下的动力特性。赵利平等[14]建立了水下爆炸和两层码头结构的全耦合模型分析了冲击波在不同深度下传至码头结构时对其造成的破坏。因此，通过数值模拟方法对典型的高桩码头结构进行水下爆炸动力响应研究是有一定研究意义的。

本文通过对东南沿海地区某典型高桩码头开展水下爆炸冲击荷载下的数值模拟，系统地研究该型高桩码头结构在不同爆炸荷载作用下的动力响应特性，并分析了该类结构的抗爆设计薄弱环节。研究结果可为该型高桩码头的抗爆设计及有效拆除提供一定的参考依据。

1 有限元模型

基于ALE多物质流固耦合法，选取东南沿海某港口工程的码头结构作为研究对象，建立全耦合模型，用于分析水下爆炸冲击作用下结构的动力响应和破坏模式。

该模型包括码头结构、炸药、空气、水和岩石5种材料模型，其中码头结构和岩石采用Lagrange网格划分，采用共节点法建模，炸药、水和空气采用ALE算法。对于码头结构，设置对称边界，同时空气和水体设置一个无反射边界的条件来加以描述，用关键字*Constrained_Lagrange_In_Solid来定义横梁和周围材料的全耦合。模型包括横梁、桩、炸药、空气、水、岩石6个部分，其中水域65.6 m×27.05 m×2.82 m，空气域为65.6 m ×7.32 m×2.82 m，共设7根桩柱，长度为25 m，直径0.45 m，桩与桩之间间隔6 m，模型共352 274个节点，309 472个单元，全耦合模型如图1所示，材料参数如表1所示。

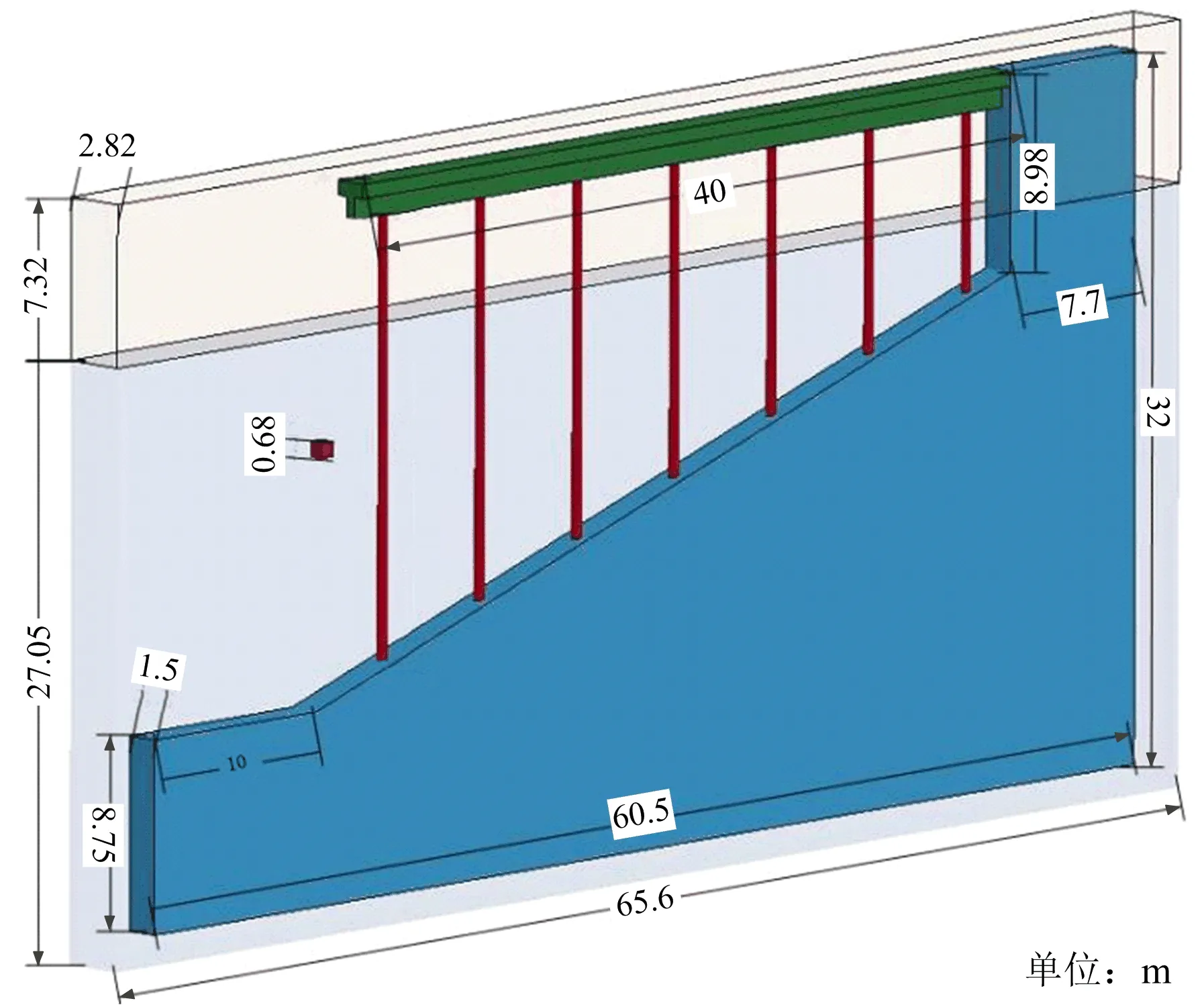
图1 数值模型Fig.1 Numerical model

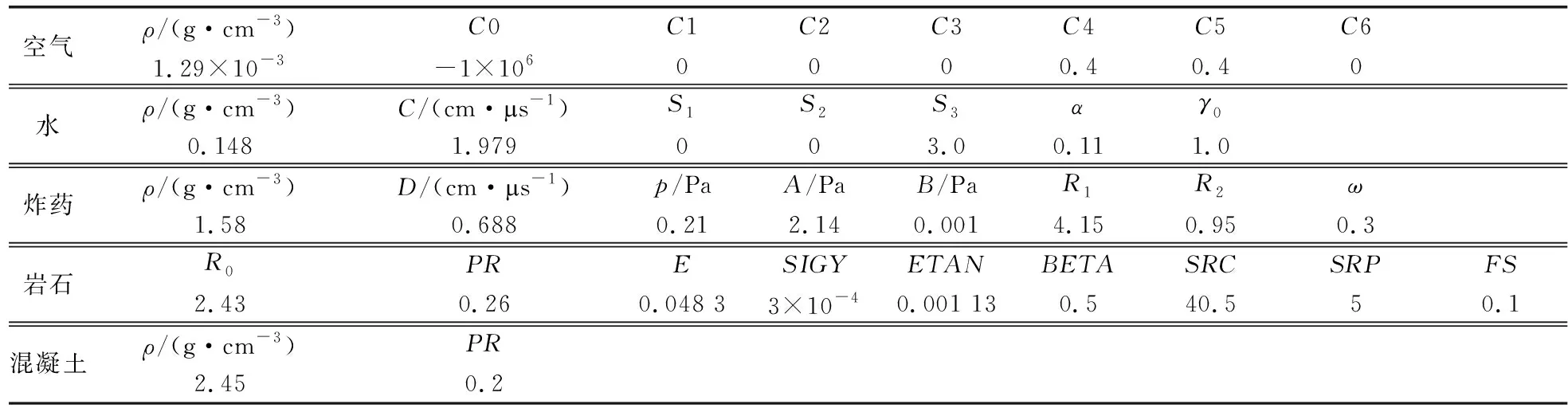
表1 材料参数

2 动力响应特性

水下爆炸冲击波在结构和水之间传播过程的压力云图(炸药当量为500 kg，距码头结构前沿爆距为4 m，爆炸深度为水下5.5 m)如图2所示。分析压力云图可知，在t=1 998 μs时刻，冲击传播通过水介质传播到第一根桩上，并对桩产生了一定力的作用。在t=3 497 μs时刻，冲击波已经到达水面并与结构相互作用，冲击波对桩产生作用的同时，流场的形态也因桩的形态而发生变化。在水面附近，由于空气的存在，发生水面截断效应；随着时间的推移，一部分冲击波在结构桩体的表面附近发生压力反射从而形成反射冲击波，以反射波的形式在水中继续传播，当反射冲击波与水下的入射冲击波相接触时会相互抵消形成低压区(见图2c)，当低压区的压力足够低时，水就会变成蒸汽形成局部空化区，空化效应会加剧结构的损伤效应。

图2 冲击波传播过程压力云图Fig.2 Stress cloud of shock wave propagation process

当冲击波作用于码头结构上时，结构在水下冲击荷载作用下会产生一定的弹塑性变形，当结构的塑性变形累计超过一定的限值时，将会导致结构发生不可逆转的塑性损伤破坏。由水下爆炸冲击波作用于结构上的损伤云图(见图3)可以看出，结构在起爆后，横梁及其周边岩石最先发生塑性变形，由于桩柱对横梁产生一个反向的压力，t=1 499 μs时，桩柱背爆面桩身区域距离爆源最近的混凝土单元最早受到破坏，并且最先达到失效阈值1，部分混凝土材料单元发生失效并被删除。结合图3，可知桩在水下爆炸冲击荷载作用下产生了一定的弯曲变形，背爆面桩身区域的混凝土单元承受了较大的拉应力，当作用于背爆面区域混凝土单元产生的拉应力值超过桩身区域混凝土材料的累积抗拉极限时，混凝土材料单元便会发生失效而直接产生桩身裂纹。随着冲击波向码头底部进一步传播，码头结构的损伤范围不断扩大。在大约t=7 497 μs时，受桩身边界条件的影响，桩身两端可视为固定支座，桩柱端部在冲击荷载作用下产生了一定的负弯矩区，桩柱迎爆面底部因较大的拉应力而逐渐屈服，产生一定的塑性破坏区。同时，由塑性损伤区的分布规律可知，在本工况下，除桩柱产生了不同程度的损伤外，第一根桩柱底部基岩区域以及与横梁相连的基岩区域塑形损伤破坏较为严重，此处基础在抗爆设计时应适当加强。

图3 爆炸冲击下码头结构的损伤云图Fig.3 Damage cloud of wharf structure under explosion impact

在模拟过程中，通过桩柱上设置监测点，检测和分析爆炸过程结构不同部分的爆炸特性。模拟共设置3个监测点,监测点1位于水下5.5 m处；监测点2位于水下0.5 m处；监测点3位于水下10.5 m处(见图4)。

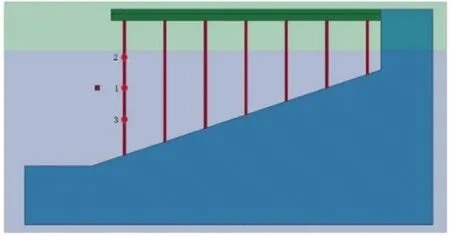
图4 监测点布置Fig.4 Layout of monitoring point

由爆点与迎爆面3个监测点的压力时程曲线(见图5)可以看出，监测点1最先达到超压峰值，既有稀疏波的反射也有水底波的反射，且主冲击波的压力值最大，监测点2和监测点3几乎同时达到超压峰值，监测点2的反射波主要以稀疏波为主，监测点3的反射波主要以水底反射波为主。可以得出，迎爆面测点距爆心越近，其超压峰值越大，也越早达到超压峰值。一定爆炸位置下，随着测量深度的增大，稀疏波的作用减弱，水底反射波的作用增强。

图5 监测点压力时程Fig.5 Pressure time history of monitoring point

3 有效性验证

对于TNT炸药情况下的水下爆炸，由Cole经验计算公式，能够准确地得到水中某点所受冲击波压力的时程曲线和峰值：

(1)

(2)

式中：pm为冲击波的峰值压力值，Pa；θ为衰减系数；m为炸药质量，kg；R为测点到爆心距离，m；R0为圆形炸药半径，m；tp为冲击波作用下的正向压力时间，s。

为保证模拟的可靠性，基于Cole经验公式，对比分析了不同起爆距离下测点1的压力峰值与Cole经验公式得出的压力峰值差异性，并绘制不同爆距处压力峰值对比(见图6)。结果表明，数值仿真结果与经验公式所计算结果的差异随起爆距离的增大而减少，当爆距过小时，误差较大，因为此时距离爆源过近，冲击波高频成分多，此时水介质受到一个强压缩，会出现一个较大的阻碍。在爆心距离超过60 cm时，两者曲线几乎重合，而模拟中所有后续仿真方案的爆心距都不小于2 m，足以保证模拟的可靠性。

图6 不同爆距处峰值压力对比Fig.6 Comparison of pressure peak at different explosion distances

分析图5中的压力时程曲线可知，在测点1的位置，主冲击波压力值为104 MPa，反射稀疏波的压力值为17.5 MPa，水底反射波的压力值为2.98 MPa，整体压力值124.48 MPa，经验公式得出的压力峰值为123 MPa，误差1.2%，说明数值模拟结果可靠。

4 爆炸冲击框架码头破坏效应

为了系统地研究码头结构的动力响应特性，从爆炸距离R、爆炸深度H以及装药量m等变量入手，通过大量模拟试验及对比分析，研究桩柱在水下爆炸荷载影响下的响应特性和破坏模式，最终选取如下7个典型工况，不同工况设置如表2所示。

表2 不同工况设置

4.1 炸药起爆距离对码头结构损伤破坏的影响

为研究起爆距离对码头结构的的动力响应特性，模拟中保持炸药的当量和起爆深度不变，仅改变炸药起爆距离，选取工况1、工况2、工况3，即炸药当量为500 kg，起爆深度为水下5.5 m，对应起爆距离分别为2、4、6 m，研究不同爆距下结构的动力响应和损伤破坏模式，不同爆炸距离模型分布如图7所示。

图7 不同爆距模型Fig.7 Model of different explosion distances

由不同起爆距离下测点的压力时程(见图8)可知，在其他条件相同的情况下，水下TNT炸药的爆炸压力峰值与测点距离成反比，工况1的测点压力峰值最大，约为263 MPa，工况2、工况3的测点压力峰值相对较小，分别为105、55 MPa，相比减少了约60%和79%，表明码头结构的测点压力随起爆距离的增大而大幅减少。

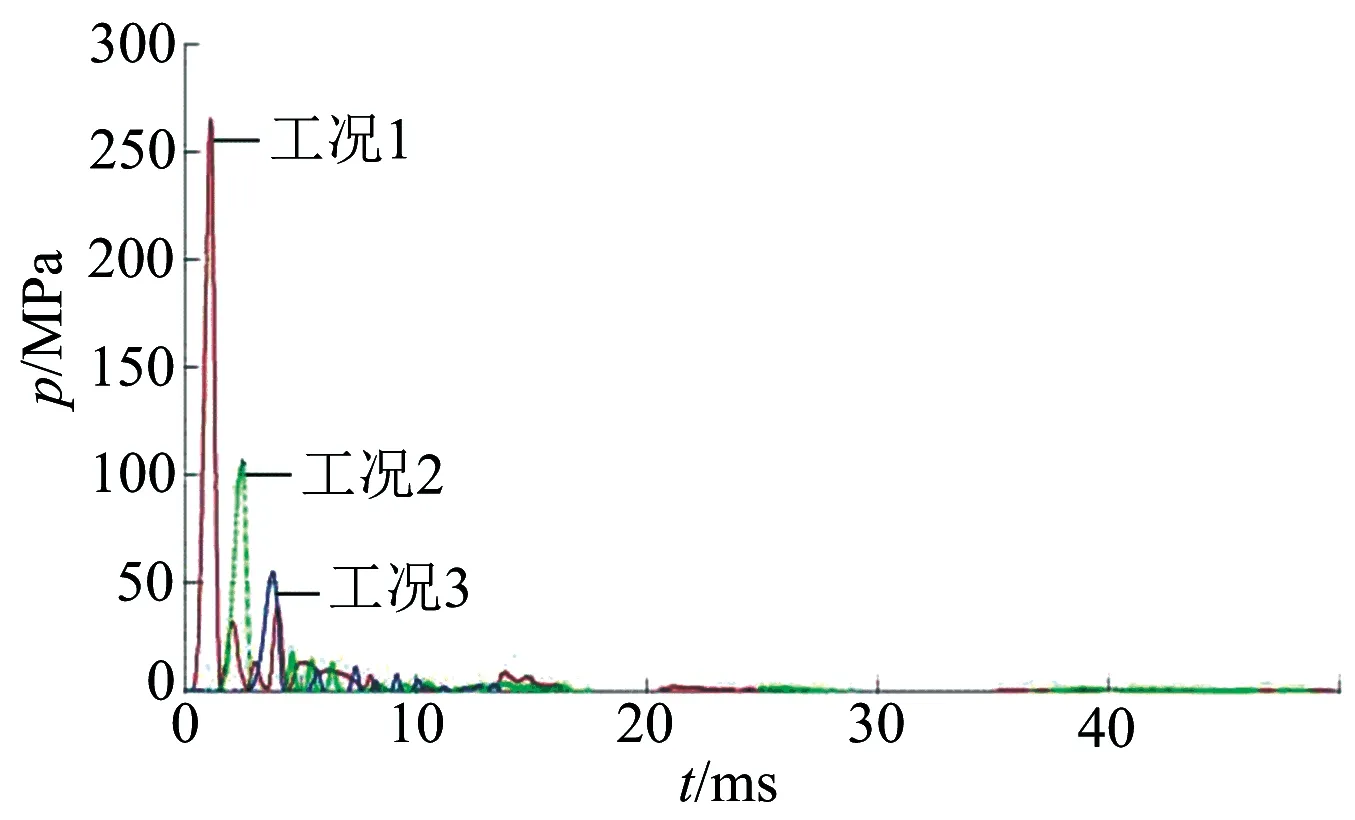
图8 不同爆距下测点的压力时程Fig.8 Pressure time history of measuring points at different explosion distances

由不同爆距下的测点位移时程(见图9)可知，对于不同起爆距离下的码头结构测点位移，其变化规律存在细微的差别，可以看出，工况1的测点位移时程曲线是一条倾斜的直线，斜率几乎没有发生过变化；而工况2和工况3在t=5 000 μs时，位移变化斜率发生过一次小幅增大，小幅增大的原因如前所述，是由于入射波和水底反射冲击波的叠加。由于工况1起爆距离较小，当冲击波作用在桩柱上时，冲击波在桩柱上的反射作用加强，桩柱上的反射波要强于水底面的反射波，因而抵消了大部分经由水底面传播到桩柱上的反射波，这是造成工况1和工况2、工况3产生差异的原因。

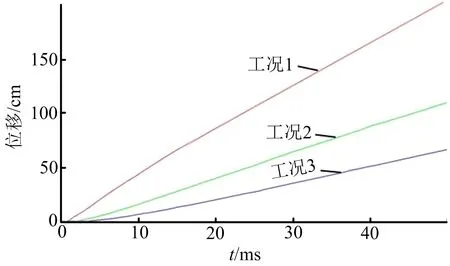
图9 不同爆距下测点的位移时程Fig.9 Displacement time histories of measuring points at different explosion distances

4.2 炸药起爆深度对码头结构损伤破坏的影响

为研究起爆深度对码头结构的的动力响应特性，模拟中保持炸药的当量和爆炸距离不变，改变爆炸的深度，选取工况2、工况4、工况5，即炸药质量为500 kg，炸药距离1号测点4 m，对应爆炸深度分别为水下2.0、5.5、9.0 m，不同爆深分布如图10所示。

图10 不同爆深分布Fig.10 Distribution of different explosion depths

通过对比分析3个不同工况下测点的压力测量曲线(见图11)可以看出，在TNT当量及爆炸距离相同的情况下，不同起爆深度的爆炸冲击波达到压力峰值的时间基本相同，但是不同的位置的反射作用对冲击波的影响较大，工况4和工况5的压力峰值相比工况2减少了80%。通过对比分析上述3种工况可知，码头结构上所承受的水下爆炸超压荷载，一部分是由爆炸冲击波直接产生并作用在码头结构上，还有一部分是水面截断效应以及水底反射而作用在结构上。且超压荷载峰值与炸药起爆点自由水面以及水底的相对距离差值有关。经分析可知，在其他条件相同的情况下，当起爆点到自由水面的距离与起爆点至基础底面距离之差的绝对值越大时，压力峰值的衰减效果会显著增大。

图11 不同爆深下测点的压力时程Fig.11 Pressure time history of measuring points at different explosion depths

由不同爆深下测点的位移时程(见图12)可以看出，在其他条件相同的情况下，起爆深度对于码头结构的动力响应特性是有显著影响的。其总体规律是，当起爆点到自由水面的距离与起爆点至基础底面距离之差的绝对值越大时，码头结构测点的位移速率变化越小，且位移峰值越小。

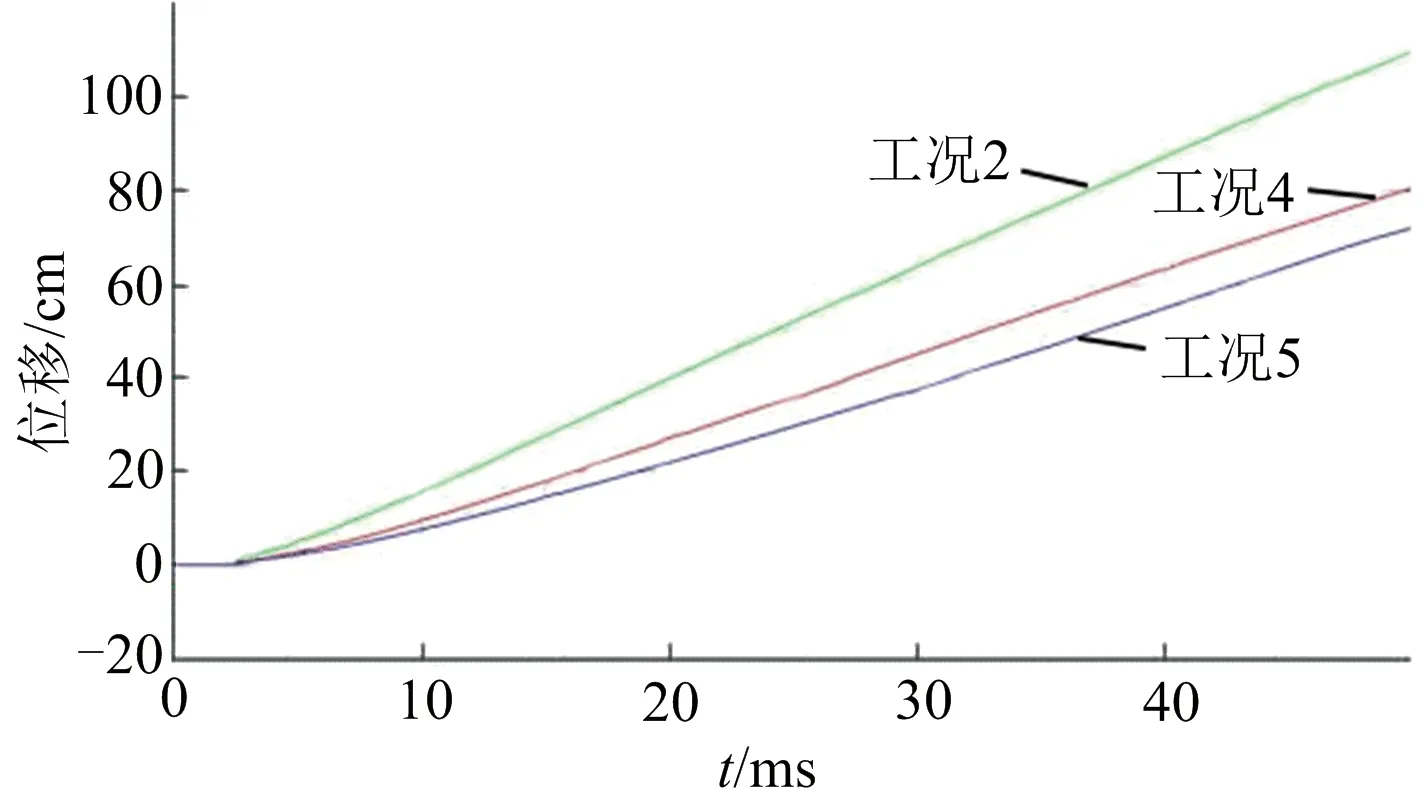
图12 不同爆深下测点的位移时程Fig.12 Displacement time histories of measuring points at different explosion depths

4.3 炸药当量对码头结构损伤破坏的影响

为研究炸药当量对码头结构的的动力响应特性，设定爆炸距离和爆炸深度不变，仅改变TNT炸药当量。选取工况2、工况6、工况7，炸药爆深为水下5.5 m，爆炸距离为码头前沿4 m，TNT炸药当量分别为500、330、210 kg。不同当量模型如图13所示。

图13 不同当量模型Fig.13 Different equivalent model

由不同当量下测点的压力时程(见图14)可以看出，在相同爆炸距离和爆炸深度的情况下，工况2、工况6、工况7的测点超压峰值分别为104、72、30 MPa，工况6、工况7相比工况2测点峰值超压，分别减少了约31%和71%。表明在其他条件相同的情况下，码头结构的测点压力峰值随TNT当量的增大而呈线型增大。

图14 不同当量下测点的压力时程Fig.14 Pressure time history of measuring points at different equivalents

由不同当量下测点的位移时程(见图15)可以看出，在不同TNT当量情况下，测点的位移变化速率是有很大区别的。其总体规律是，TNT当量越大，测点的位移速率变化越大。经分析还可以看出，在t=5 000 μs左右，位移变化速率出现一次低幅度的提高，这是水底反射冲击波与入射波的叠加导致的，此后位移速率基本保持在这个相对稳定的量级，曲线斜率基本没有发生变化。

图15 不同当量下测点的位移时程Fig.15 Displacement time history of measuring point at different equivalent

4.4 无量纲化的压力峰值分析

将所有工况进行无量纲化处理，绘制三维曲线(见图16)可以看出，当相对爆距为0.252 m/kg3，相对爆深为0.693 m/kg3时，水下爆炸荷载作用于码头结构上的压力峰值较大，此类情况下需要对码头结构进行更多的防护设计。

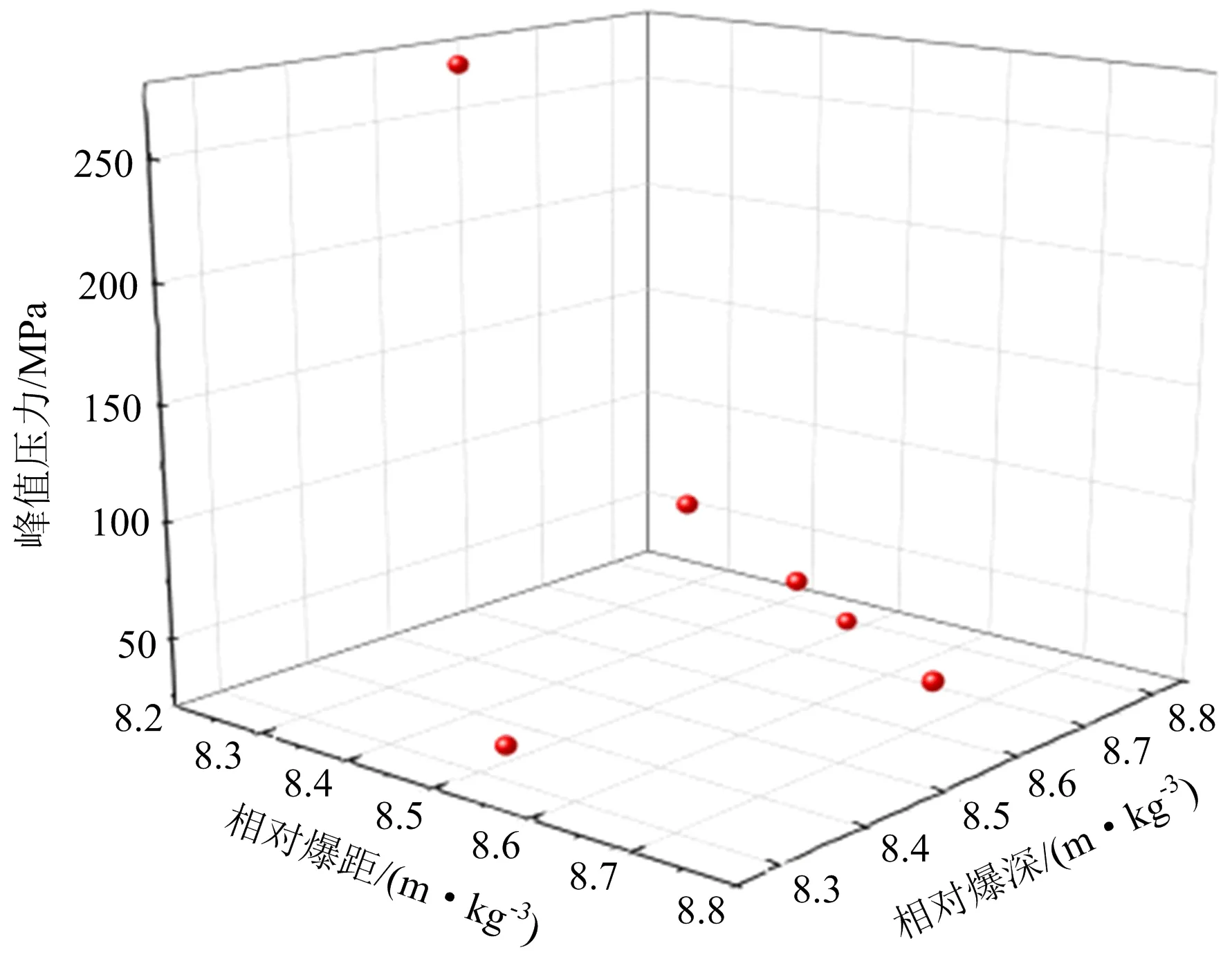
图16 相同爆距和相同爆深下监测点1的峰值压力Fig.16 Peak pressure of monitoring point 1 under the same explosion distance and explosion depth

5 结论

1)在水下爆炸荷载的作用下，所有的桩柱产生了不同程度的损伤，码头端部的第一根桩柱底部基岩区域以及与横梁相连的基岩区域塑形损伤破坏较为严重，此处的水下基础在码头抗爆设计时应适当加强。

2)当TNT炸药的起爆距离较小时，桩柱上的反射波要强于水底面的反射波，并会与之相抵消，作用在桩柱上的反射稀疏波会随之削弱。

3)在其他条件相同的情况下，当起爆点到自由水面的距离与起爆点至基础底面距离之差的绝对值越大时，压力峰值的衰减效果会显著增大。

4)当相对爆距为0.252 m/kg3，相对爆深为0.693 m/kg3时，水下爆炸荷载作用于码头结构上的压力峰值较大，在进行码头结构抗爆防护设计时，应考虑该种特殊情况。