双重变异遗传算法及其在临界滑动面搜索中的应用
覃 伟
(重庆工程职业技术学院,重庆 402260)
在公路工程、建筑工程、矿山工程、水利工程等领域中,常会遇到大量的边坡稳定性问题。确定边坡临界滑动面对边坡稳定性分析及坍岸宽度预测等研究具有重要意义[1]。
边坡临界滑动面的搜索,本质上是一个优化问题,其具有变量多、约束条件复杂、局部极值点多、非凸性等特点,使得传统的优化算法(如模式搜索法)在搜索临界滑动面时,常常陷入局部极值点,给边坡的稳定性分析带来许多困难。
遗传算法(genetic algorithm,GA)由 Holland 教授于 20世纪 70 年代提出,是一种模拟达尔文遗传选择和自然淘汰的生物进化过程的搜索寻优算法,具有思想简单、易于编程实现、算法健壮等优点,同时还具有隐含并行性和全局搜索等显著特性[2]。因此,一些学者将遗传算法运用到边坡临界滑动面搜索研究中,取得了一定成效[3−8]。如,贺子光等[3]将单纯形法和回溯机制引入GEP 中,提出了混合GEP 方法搜索边坡的临界滑动面;梁冠亭等[4]采用自适应遗传优化算法搜索采用抗滑桩支护边坡的临界滑动面;朱剑锋等[5]提出自适应禁忌变异遗传算法搜索土钉墙临界滑动面。但是目前的标准遗传算法及其改进算法仍在不同程度上存在收敛速度较慢、容易进入早熟等缺陷,有待进一步改进和完善。
本文在传统遗传算法的基础上,提出双重变异策略对遗传算法进行改进,形成双重变异遗传算法(DMGA),并结合简化Bishop 法,编写Python 程序,通过对土坡算例临界滑动面的计算,进一步为边坡临界滑动面搜索提供有效方法。
1 临界滑动面搜索问题的目标函数
求解边坡的临界滑动面,即是搜索使边坡安全系数最小的滑动面。边坡稳定性计算方法有很多,主要包括刚体极限平衡方法和数值模拟方法[9−10]。对于滑动面呈圆弧形的土质边坡,由于简化Bishop 法计算简单、物理意义明确,在工程实践中应用广泛。因此本文采用简化Bishop 法计算土质边坡的稳定性。
1.1 简化Bishop 法
简化Bishop 法是一种适用于滑动面呈圆弧形的边坡的稳定性分析方法。其中边坡安全系数F的计算公式[11]为:
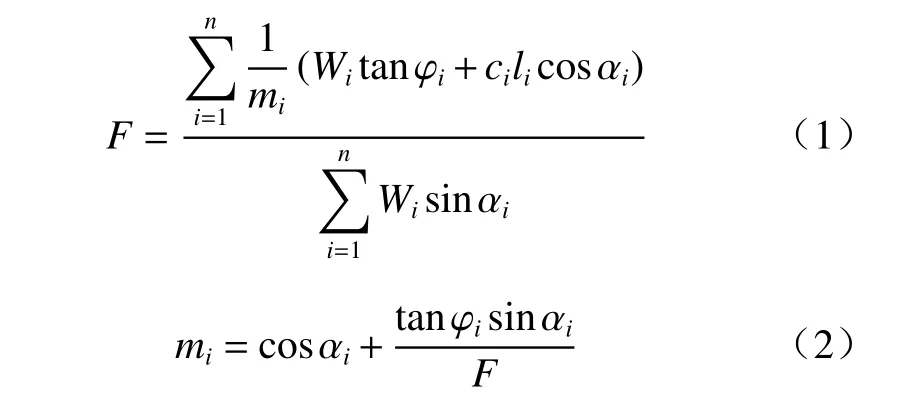
式中:ci—第i条块滑动面上岩土体的黏聚力/kPa;
φi—第i条块滑动面上岩土体的内摩擦角/(°);
li—第i条块滑动面的弧长/m;
Wi—第i条块的单宽重量/(kN· m−1);
αi—第i条块滑动面倾角/(°),当滑动面倾向与滑动方向一致时,αi取正;当滑动面倾向与滑动方向相反时,αi取负。
当变量mi很小时,计算结果与实际情况不符。根据一些学者的意见,当mi⩽0.2时,不能采用简化B ishop 法计算边坡安全系数[11]。
1.2 目标函数的确定
边坡临界滑动面的位置与圆弧形滑动面的圆心半径R、圆心横坐标xo、圆心纵坐标yo有关,因此将这3 个量作为目标函数的求解变量。
并不是任意半径及圆心位置的圆弧都能计算出边坡的安全系数,如发生圆弧与边坡不存在交点,或所采用的边坡安全系数计算方法不适用等情况。因此,临界滑动面搜索问题可表示为在一定约束条件下求解边坡安全系数最小值,即求解下面约束问题:

运用外点罚函数法[12]将该约束问题转化为无约束问题:

其中:
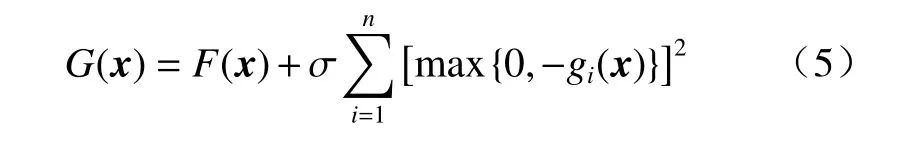
其中,当圆弧滑动面与坡体无交点时,F(x)不存在,则令其为一较大值100;σ为很大的正数,取值1 000。
2 双重变异遗传算法的设计
2.1 个体编码与初始种群产生
本文对变量采用一种特殊的实数编码,在编码中设置符号基因位与数字基因位。符号基因位存放实数的符号信息,当实数为正或0 时,该基因位的值取1;实数为负时,该基因位的值取−1。数字基因位存放实数的数字部分,实数各位上的数字占一个基因位,且该位上的数字即为对应基因位的值。对每个变量xi均采用上述实数编码,并将它们的编码依次连接构成一个染色体。例如,若目标函数的解由3 个变量构成,其中变量x1为36.12,变量x2为−5.099,变量x3为72.562,则对其进行实数编码如图1所示。
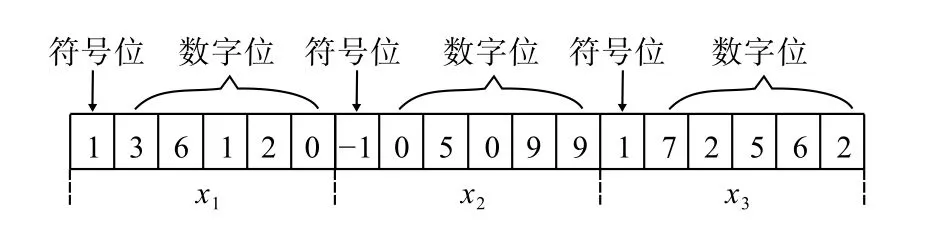
图1 实数编码Fig.1 Real number coding
初始种群内的个体数为N,每个个体通过随机数产生,个体染色体中的每个数字基因位随机生成[0,9]区间的整数,每个符号基因位随机生成1 或−1,若该变量不为负,则对应符号基因位仅产生1。
2.2 适应度值函数
遗传算法在进化时,以个体的适应度值作为搜索依据。求解优化问题时,需要将目标函数转化为适应度函数。由于目标函数G(x)为最小值问题,构造适应度值函数如下:
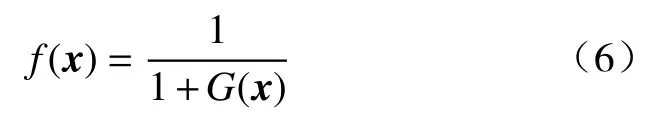
适应度函数值f(x)越大,边坡的安全系数就越小。
2.3 双重变异遗传算法的进化过程
2.3.1 选择操作
父代个体的适应度值确定后,按照适应度值进行个体的选择。本文种群的选择采用精英保留策略[13−14],每一代种群进化完成后,首先从中找出适应度值最大的一个个体,直接让其进入下一代,不再对其进行交叉、变异操作。剩余的个体,则采用转盘式选择方式进行选择操作,转盘式选择的基本原理是根据每个个体的适应度值的比例来确定该个体的选择概率[15]。
转盘式选择的计算方法:先根据个体的适应度值fi按式(8)计算个体的选择概率pi,并令p0=0,然后生成[0,1]区间的随机数r,如果r满足式(7),则选择个体j。

其中:

2.3.2 自适应交叉操作
在遗传算法中,通过交叉操作既可以使种群多样化,又可以引导搜索方向,促进优秀个体的产生。本文采取单变量交叉方式,即从种群中选出任意2 个个体(个体1、个体2)进行交叉,当产生的[0,1)区间的随机数小于交叉概率Pc时,随机选择一个变量xi,使个体1 与个体2 中变量xi所对应的基因位的值进行交换。
交叉概率是影响遗传算法性能的关键因素之一。卢明奇等[16]为了解决传统的自适应遗传算法在进化初期常存在停滞现象、进化后期易陷入局部极值点的问题,提出了一种改进的自适应交叉概率。但该方法参数较多,增加了参数设置的难度。本文在考虑适应度值及进化代数的情况下,提出一种复合自适应交叉概率,使交叉概率Pc随个体适应度值及进化代数进行调整,Pc的计算公式如下:

式中:fmax—当前种群中的最大适应度值;
f′—待交叉个体中较大的适应度值;
—当前种群的平均适应度值;
T—总的进化代数;
t—当前进化代数。
2.3.3 双重变异操作
在传统的遗传算法中,变异操作本质上是随机搜索,并不能保证产生改进的后代[17],进而常导致遗传算法的收敛速度较慢。为此,本文借鉴模式搜索法中探测移动的思想,提出探测变异操作,并与传统的直接变异操作相结合,构成双重变异策略对遗传算法进行改进,使遗传算法的收敛速度及全局搜索能力得到提升。双重变异操作包括探测变异操作与直接变异操作。其中,探测变异操作将提升算法的局部寻优能力,直接变异操作将使算法具备全局寻优能力。
为了叙述方便,将采用双重变异策略的遗传算法称为双重变异遗传算法(DMGA),将仅采用探测变异策略的遗传算法称为探测变异遗传算法(DEMGA),将仅采用直接变异策略的遗传算法称为直接变异遗传算法(DIMGA)。
(1)探测变异操作
探测变异的具体操作是在随机选择1 个基因位后分5 种情况进行。
情况1:若选择的是符号位变异,则直接进行变异探测,并计算适应度值,判断是否发生变异(图2)。

图2 探测变异操作情况1 示意图Fig.2 Schematic diagram of the first case of detecting mutation operation
情况2:若选择的基因位为变量xi的第1 个数字位,则直接进行变异探测,并计算适应度值,判断是否发生变异。该变异探测分3 种子情况(图3)。子情况1,若该位的值为0,则变异为[1,9]区间的随机整数;子情况2,若该位的值为9,则变异为[0,8]区间的随机整数;子情况3,若该位的值为[1,8]区间的整数m,则变异分两个方向进行探测,一个方向是变异为[m+1,9]区间的随机整数,另一个方向是变异为[0,m−1]区间的随机整数,然后将适应度值较大者与变异前适应度值进行比较,判断是否变异。

图3 探测变异操作情况2 示意图Fig.3 Schematic diagram of the second case of detecting mutation operation
情况3:若选择的基因位位于变量xi第1 个数字位之后,且该位的值位于区间[1,8],则直接进行变异探测(同情况2 的子情况3),并计算适应度值,判断是否发生变异。
情况4:若选择的基因位位于变量xi第1 个数字位之后,且该位的值为0,则该变异探测分2 种子情况(图4)。子情况1,当其前一位的值等于0 时,则该位变异为[1,9]区间的随机整数;子情况2,当其前一位的值大于0 时,则变异分两个方向进行探测,一个方向是该位变异为[1,9]区间的随机整数m,另一个方向是该位值也变异为m,且前一位的值作减1 变异,然后将适应度值较大者与变异前适应度值进行比较,判断是否变异。

图4 探测变异操作情况4 示意图Fig.4 Schematic diagram of the fourth case of detecting mutation operation
情况5:若选择的基因位位于变量xi第1 个数字位之后,且该位的值为9,则该变异探测分2 种子情况(图5)。子情况1,当其前一位的值等于9 时,则该位变异为[0,8]区间的随机整数;子情况2,当其前一位的值小于9 时,则变异分两个方向进行探测,一个方向是该位变异为[0,8]区间的随机整数m,另一个方向是该位值也变异为m,且前一位的值作加1 变异,然后将适应度值较大者与变异前适应度值进行比较,判断是否变异。

图5 探测变异操作情况5 示意图Fig.5 Schematic diagram of the fifth case of detecting mutation operation
(2)直接变异操作
直接变异操作是指将待变异个体的每个变量xi所对应的染色体等分为前后两段,在每一段中随机选择1 个基因位进行直接变异,变异后的适应度值不控制变异的发生。直接变异能够提供种群的多样性,避免早熟的产生。
“昆南”阴平声字“他”的唱调(《南西厢·佳期》【十二红】“爱他两意和谐”,687),其中的即为两节型过腔。虽然这个过腔的音乐材料都相同,都来自于本唱调音阶的级音,但由此组成的乐汇或句型可以分作两节,为第一节级音性过腔,为第二节级音性过腔。这个过腔即是由同一种音乐材料组成的两节型过腔。
(3)双重变异操作
当待变异个体适应度值f接近当前最佳个体时,希望待变异个体能够具有局部寻优能力,同时也具有跳出局部极值点,搜索全局最优的能力;当待变异个体适应度值f距离当前最佳个体较远时,希望个体向着适应度值增加的方向变异。将探测变异与直接变异结合在一起形成双重变异操作,便可以实现上述目标。
双重变异操作的实施策略:
(4)变异概率
变异操作是在一定的概率下发生的,当产生的[0,1)区间的随机数小于变异概率Pm时,将会发生变异。变异概率的大小决定着新个体产生的机会及计算量的大小。较小的变异概率,产生新个体的机会较小;较大的变异概率,遗传算法的计算量较大,且趋于纯粹的随机搜索算法。
为了能达到好的寻优效果,在进化的早期期望能有较大的变异概率,以增加搜索的广度;在进化的晚期期望能有较小的变异概率,以提高进化的速度。同时,也希望当待变异个体适应度值接近当前最佳个体时,减小变异概率,使较好的个体得到保留;当待变异个体适应度值距离当前最佳个体较远时,有较大的变异概率,使较差的个体容易被淘汰。
基于上述原因,本文在综合考虑待变异个体的适应度值f及进化代数对变异概率影响的情况下,提出一种复合自适应变异概率Pm,其计算公式如下:
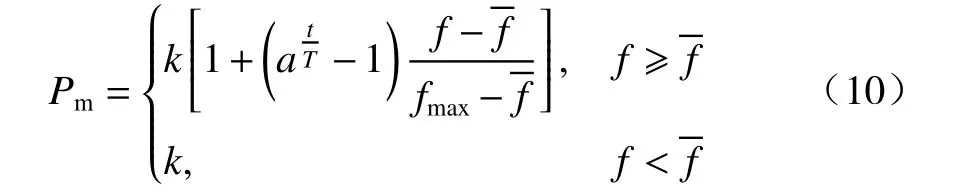
其中,a为区间(0,1)内的常数,a越大,变异概率Pm越大;k为区间[0,1]内的常数,k越大,变异概率Pm也越大。反映了待变异个体的适应度值距离当前种群中的最大适应度值的相对距离;当一定时,Pm将随t的增大而减小,即进化早期变异概率较大,使算法有较大的搜索广度;当t一定时,越大,Pm就越小,即待变异个体适应度值越接近当前最佳个体,较好的个体就更容易得到保留。
2.4 双重变异遗传算法的计算步骤
步骤一:随机生成实数编码(图1)的初始种群,初始种群中的个体数为N,且N为偶数。
步骤二:将个体染色体解码为实数,根据式(6)计算初始种群中每个个体的适应度值,并令当前进化代数t=0。
步骤三:根据式(8)计算选择概率,并令j=0。
步骤四:如果j=0,将种群中适应度值最大的一个个体直接选出,不进行后续的交叉及变异操作,直接复制到下一代,然后根据式(7)采用转盘式选择方式选择1 个个体,进行步骤六;如果j>0,根据式(7)采用转盘式选择方式选择2 个个体,进行步骤五。
步骤五:将选出的2 个个体进行单变量交叉操作,进行步骤六。交叉操作方法:当产生的[0,1)区间的随机数小于交叉概率Pc时,随机选择一个变量xi,使个体1 中变量xi所对应的基因位的值与个体2 的进行交换。其中,交叉概率Pc根据式(9)计算得到。
步骤六:对个体进行双重变异操作,进行步骤七。双重变异操作方法:当时,产生一个[0,1]的随机数 γ,若γ>0.5,采用探测变异;若γ ⩽0.5,采用直接变异。当时,采用探测变异。探测变异操作、直接变异操作按2.3.3 节所述方法进行。变异概率Pm按式(10)计算。
步骤七:如果(j+1)×2 步骤八:将新生成的种群个体的染色体解码为实数,根据式(6)计算适应度值。如果t==T,计算结束;如果t 说明:本文所述的直接变异遗传算法、探测变异遗传算法与双重变异遗传算法的计算步骤的不同之处主要体现在步骤六。若将步骤六改为:“对个体进行直接变异操作”,则为直接变异遗传算法的计算步骤;若将步骤六改为:“对个体进行探测变异操作”,则为探测变异遗传算法的计算步骤。 本文将双重变异遗传算法(DMGA)与简化Bishop法相结合编写Python 程序,以1987年澳大利亚计算机应用协会(ACADS)设计的考核题1(a)、考核题1(c)[18]为求解对象,对这两道题分别进行50 次独立计算,并以ACADS 提供的裁判程序答案检验算法的寻优效果。然后,在分别仅进行直接变异、探测变异的情况下,对上述两题也进行50 次独立计算,对比分析DMGA 算法的性能。 考核题1(a)为一均质土质边坡,如图6所示,坡高10 m,坡度为26.565°,黏聚力为3 kPa,内摩擦角为19.6°,土体重度为20 kN/m3。要求确定边坡的临界滑动面及最小安全系数。 图6 考核题1(a)坡面示意图(坐标平移后)[18]Fig.6 Profile of slope in EX1(a)(after coordinates are modified)[18] 考核题1(c)为一非均质土质边坡,如图7所示,坡高10 m,坡度为26.565°,黏聚力、内摩擦角及土体重度见表1。要求确定边坡的临界滑动面及最小安全系数。 图7 考核题1(c)剖面图(坐标平移后)[18]Fig.7 Profile of slope in EX1(c)(after coordinates are modified)[18] 表1 考核题1(c)的材料性质[18]Table 1 Material characteristic in EX1(c)[18] ACADS 给出的考核题1(a)边坡最小安全系数的裁判程序答案有:0.990,0.991,1.000;考核题1(c)边坡最小安全系数的裁判程序答案有:1.385,1.390,1.406。 本文给定圆弧滑动面半径R、圆心横坐标xo、圆心纵坐标yo的搜索区间分别为:R∈(0,99],xo∈ [−99,99],yo∈[0,99]。 计算所涉及的相关参数取值如下: (a)滑体土条宽度按R/50 进行取值,且单个条块不跨越地形剖面的转折点。当含有地形转折点、滑动面剪出口及滑动面后缘的条块,其宽度不足R/50 时,上述相应控制点即为条块端点; (b)变异概率计算公式(10)中参数a=0.5,k=0.6; (c)实数编码的串长为18(每个变量的编码长度为6,且变量精确到3 位小数),如图1所示; (d)种群数N 为50; (e)初次最大进化代数T为200,当最大进化代数与最佳个体出现代数之差小于等于30 时,最大进化代数增加30 代,最大进化代数的最大值为500。 3.3.1 双重变异遗传算法计算结果 表2、表3 分别是基于双重变异遗传算法对考核题1(a)、1(c)的计算结果(限于篇幅,仅列出了部分计算结果)。 表2 考核题1(a)的计算结果(DMGA)Table 2 Calculated results of EX1(a)(DMGA) 表3 考核题1(c)的计算结果(DMGA)Table 3 Calculated results of EX1(c)(DMGA) 计算结果统计显示,对于考核题1(a),50 次计算中,安全系数的最小值为0.985 2,最大值为0.993 7,平均值为0.985 7,与该考核题的裁判程序答案基本一致,说明对于均质边坡该算法可靠有效;对于考核题1(c),50 次计算中,安全系数的最小值为1.394 9,最大值为1.407 0,平均值为1.397 9,与该考核题推荐的裁判答案基本一致,说明对于非均质边坡该算法也可靠有效。 3.3.2 三种算法计算结果比较 基于双重变异遗传算法(DMGA)、直接变异遗传算法(DIMGA)、探测变异遗传算法(DEMGA),分别对两道考核题计算50 次的统计结果(表4)显示,DMGA算法搜索得到的安全系数平均值小于DIMGA 算法、DEMGA 算法的计算结果,说明DMGA 算法具有更强的全局搜索能力。并且DMGA 算法计算所得的标准差较小,说明该算法具有较好的鲁棒性。 表4 考核题1(a)、1(c)的计算结果统计分析Table 4 Statistical analysis of computation results of EX1(a)and EX1(c) 3.3.3 三种算法计算过程对比 (1)单次计算的进化过程对比 图8 为采用DMGA 算法、DIMGA 算法、DEMGA算法对考核题1(a)、1(c)进行的第1 次计算的进化过程曲线;表5 为采用DMGA 算法、DIMGA 算法、DEMGA算法对考核题1(a)、1(c)进行的第1 次计算的收敛过程对比表。图8 显示DEMGA 算法在计算考核题1(a)时,最大适应度值曲线明显偏低,表明陷入了局部极值点;DIMGA 算法计算的最大适应度值曲线在进化早期明显偏低,且对考核题1(a)、1(c)分别在第116代和第151 代才收敛(表5),表明其收敛速度较慢;DMGA 算法分别在第66 代和第72 代时收敛,其计算得到的安全系数低于DIMGA 算法和DEMGA 算法,显示出优于DIMGA 算法和DEMGA 算法的寻优能力。 表5 考核题1(a)、1(c)算法收敛过程对比表Table 5 Comparison of convergence processes of EX1(a)and EX1(c) 图8 考核题1(a)、1(c)第1 次计算的进化过程曲线Fig.8 Evolution curve of the first calculation of EX1(a)and EX1(c) (2)50 次计算的平均进化过程对比 为了进一步对比三种算法进化过程的统计变化规律,根据各算法50 次计算的历代最佳个体的适应度值计算出历代最佳个体的平均适应度值,绘制出前200 代的平均进化过程曲线(图9)。曲线显示,与上述单次计算对比类似,DEMGA 算法的局部寻优能力较强,在进化的早期,能快速搜索到局部极值点附近,但其跳出局部极值点的能力弱,容易出现早熟现象;DIMGA 算法具有全局搜索的特点,局部寻优能力较弱,收敛速度较慢;DMGA 算法将探测变异与直接变异结合,既具有较强的局部搜索能力,又具有较强的跳出局部极值点的能力,能够在搜索的广度与深度上达到较好平衡,因此其全局寻优能力强。 图9 考核题1(a)、1(c)的平均进化过程曲线Fig.9 Average evolution curve of EX1(a)and EX1(c) 某海堤边坡[19−20] 为一非均质土质边坡,其剖面及土层物理力学参数如图10所示,现采用双重变异遗传算法结合简化Bishop 法搜索该边坡的临界滑动面及最小安全系数。 图10 边坡剖面图[19−20]Fig.10 Slope profile[19−20] 圆弧滑动面半径及圆心坐标的搜索区间分别为:R∈(0,99],xo∈[−99,99],yo∈[0,99]。且需满足约束条件[20]:6≤yo≤30。式(10)中的参数k=0.7,其他参数设置与3.2 节相同。 经过1 次独立计算,根据历代的适应度值(最大值、平均值)与进化代数做出进化过程曲线(图11),该曲线显示了历代进化的个体适应度值的变化情况。在进化的初期(第7 代之前),种群的最大适应度值接近于0,说明进化初期种群中的个体均位于非可行域内。第7 代之后,遗传进化使种群中的一部分个体进入可行域,种群的最大适应度值及平均适应度值总体上随进化代数的增加而增加。当进化到第83 代时,种群的最大适应度值为0.370 89,随后直到第200代进化结束时均未更新,算法收敛。 图11 进化过程曲线Fig.11 Evolutionary process curve 计算结果显示,边坡的安全系数F=1.696 2,临界滑动面的圆心坐标xo=6.859 m,yo=11.910 m,半径R=14.910 m,临界滑动面左侧与坡面交点的横坐标为xL=−2.11 m,临界滑动面右侧与坡面交点的横坐标为xR=20.55 m。与文献[20]采用简化Bishop 法计算的滑面位置(xL=−2.29 m,xR=20.17 m,yo=11.65 m)基本一致,且安全系数小于文献[20]计算的最小值(Fmin=1.727),说明算法可靠有效,且寻优效果更佳。 (1)本文提出的双重变异遗传算法,能够在搜索的广度与深度上达到较好平衡,使待变异个体适应度值距离当前最佳个体较远时,能够向着适应度值增加的方向进行搜索;待变异个体适应度值接近当前最佳个体时,算法既具有局部寻优能力,也具有跳出局部极值点,搜索全局最优的能力。 (2)与仅进行直接变异或探测变异的遗传算法相比,双重变异遗传算法具有更强的全局搜索能力及鲁棒性,与简化Bishop 法结合,能够有效地搜索出边坡的圆弧形临界滑动面。3 澳大利亚计算机应用协会考核题分析
3.1 考核题及其裁判程序答案
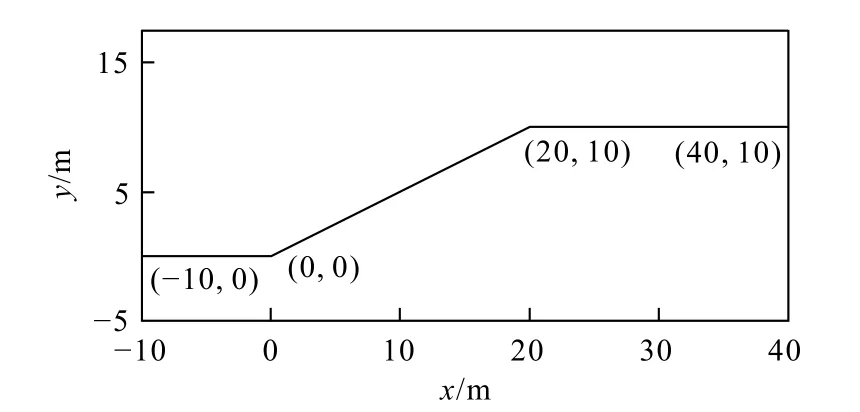
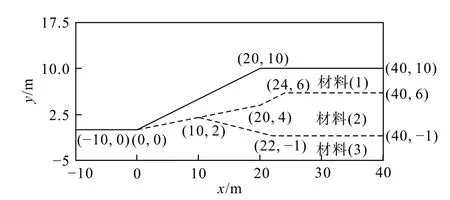
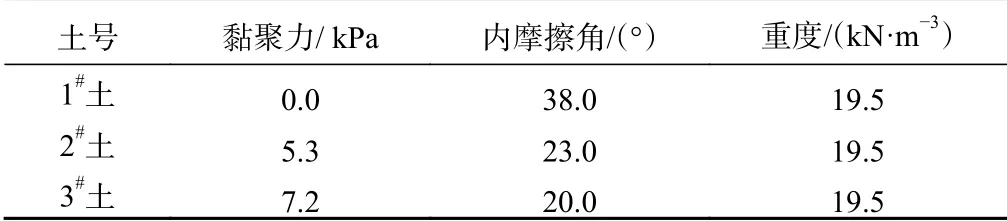
3.2 计算参数
3.3 计算结果及过程分析


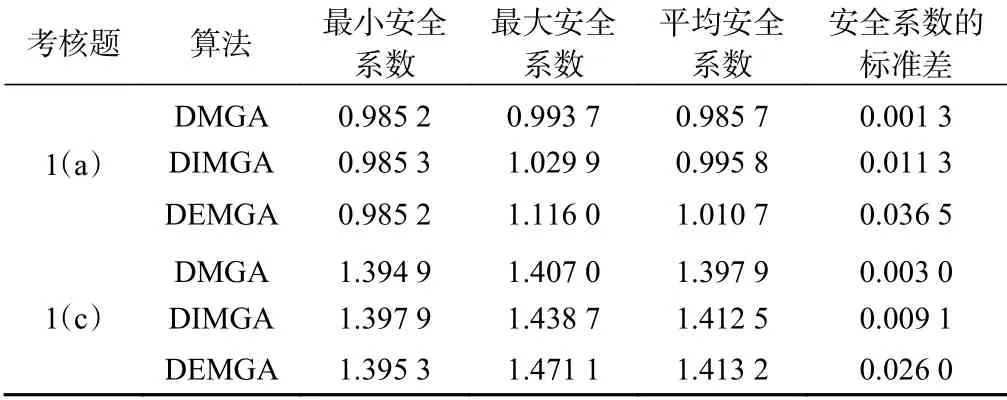

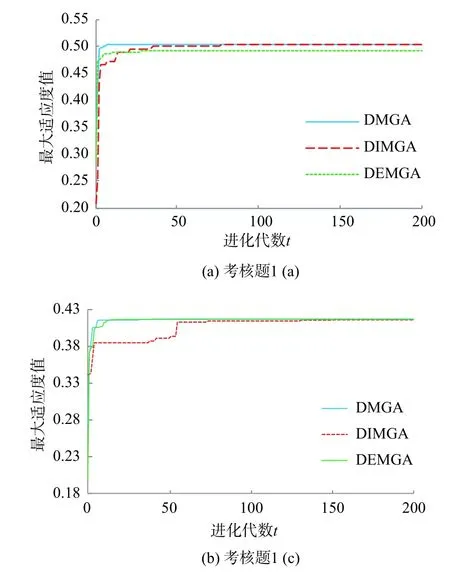

4 工程实例


5 结论

