基于离散元法的砂石混合体直剪试验结果分析

苏永华，王 栋

（湖南大学土木工程学院，湖南 长沙 410082）

对于地表高程较大甚至悬殊区域，在建、构筑物施工前都要进行一定的或较大、甚至大规模的回填处理，这种状况下建、构筑物下的地层就称为重塑地层，砂石地层是常见的重塑地层之一，在基坑、路基等工程中广泛存在。砂石混合体由力学性质以及结构相差极大的材料组成，是典型的土石混合体。砂石混合体构成的地层由于颗粒粒度变化较大、分布不均匀、块石形态各异等原因，在实际工程中易出现沉陷或塌陷等问题[1−2]，因此，砂石混合体力学性质研究是亟需进行的研究课题之一。

室内试验是研究土石混合体力学性质的基本方法，考虑不同影响因素对宏观力学性能的影响是研究的重点。但室内试验往往受尺寸效应和试验条件等因素的影响，存在可重复性差、耗时较久、不易对颗粒形状进行分析的限制。随着计算机的发展，颗粒流模拟（PFC）成为研究土石混合体力学性质的一种方法，它能够模拟微观层面的结构，充分考虑砂石混合体离散性的特点，从不同角度探讨力学性质，如：颗粒实际形状、颗粒转动、力链演化和孔隙变化等[3]。

砾石形状是砂砾石力学特性研究的重要属性参数，目前许多学者采用规则图像对砾石进行描述，如圆形、正多边形，没有考虑砾石的真实形状，很难反映出砾石真实的力学性质。许多学者利用数字图像处理技术获取真实的细观结构模型，如徐文杰[4]、廖秋林等[5]通过实际拍摄的数码图像生成土石混合体结构模型。还有学者通过识别自然块石的轮廓构建块石数据库，实现块石二维[6]、三维[7]随机模型建立，数字图像处理技术可以在不忽略砾石真实形状的前提下，对形状参数进行细致化分析，探究其影响作用。

粒度分布影响着土石混合体的变形、强度等物理力学特性。在现有的岩土工程散体材料的粒度分布描述中，大多是采用特征粒径、不均匀系数和曲率系数等参数来描述粒度分布，这些指标只能表示某些关键点的信息，缺乏对粒度整体分布的描述。针对上述情况，杜修力等[8]通过对多组试样的研究，发现土石混合体的粒度分布均满足分形结构，可以利用粒度分维值定量描述。舒志乐等[9]建立了土石混合体的二重分形结构模型，对土石混合体的粒度分维值与抗剪强度关系进行分析。

本文通过数字图像处理技术获取砾石边界信息，建立砾石形状数据库。结合分形理论建立了砂石混合体二重分形结构模型。通过颗粒流软件对不同粒度分布、颗粒形状的砂石混合体进行直剪试验，并对结果进行分析，为进一步研究砂石混合体重塑地层塌陷机理奠定基础。

1 砂石混合体随机模型构建关键步骤

1.1 基于砾石形状数据库构建离散元模型

通过数字图像处理技术获取砾石的边界坐标和形状参数，并导入PFC 中生成颗粒簇模板以供模型构建时调用，详细步骤如下：

（1）图像获取及预处理：通过高精度数码相机获取大量砾石图像，但是砾石因光线等环境因素图像会出现大量噪音，需要利用图像处理软件对图像进行消噪，并使每张图片仅显示1 个砾石（图1a）。

图1 数字图像处理技术获取边界信息流程示意图Fig.1 Flow chart showing the digital image processing technology to obtain boundary information

（2）边缘提取：预处理后的图像需进行二值化处理，可通过设定合适阈值，使图像变得简单，凸显感兴趣目标轮廓，处理后图像呈现明显的黑白效果（图1b）。二值化图像可通过边缘检测获取砾石边界，本文利用MATLAB 软件中内嵌的Canny 算法提取砾石边界（图1c）。

（3）边界拟合：通过上述方法提取的边界点数目过多，会对后续工作产生较大负担，需要对边界进行拟合，拟合方法如下[6]：选定初始点，然后顺时针获取所有边界点，依次计算边界点和初始点的距离，如果该距离满足式（1）则保留该点为拟合后的边界点，并作为下一轮的初始点，依此循环直至回到初始点。

式中：d—拟合后两个相邻边界点的距离；

D—与砾石颗粒面积相等的等效圆直径；

α—控制边界拟合精度的参数。

通过调整 α可以控制砾石边界的拟合精度。α越大所需边界点越少，但精度越低。本文选取 α为0.1，此时砾石的形状和原图像基本一致（图1d），坐标点的数量也满足后续的数值模拟需求。

（4）图像标准化处理：为了方便后续对砾石大小、旋转角度等参数的控制，需进行标准化处理，如粒径统一化、形心归零化、长轴水平化。

（5）PFC 颗粒簇模板生成：获取的砾石边界信息不能直接被PFC 识别，需要将其转换为矢量数据格式文件（dxf）。本文利用Python 第三方库dxfwrite 完成批量转换，导入PFC 并利用内置的颗粒填充算法，就可生成砾石的颗粒簇模板。

1.2 形状参数分析

颗粒形状是研究砂石混合体宏观力学行为的一个重要参数。根据相关研究[10]，颗粒可以通过轴向系数和圆度进行描述，其中轴向系数S为：

式中：LA,max，LA,min—砾石颗粒等效椭圆的长轴和短轴。

砾石颗粒的圆度公式定义为R：

式中：L，A—颗粒的周长和面积。

通过砾石形状数据库可导出形状参数，并利用数据分析软件得出圆度和轴向系数的频率分布直方图（图2），圆度分布在1.0～1.35 之间，均值为1.15，圆度指标可有效地表征颗粒整体形状接近圆的程度。圆度越大，其形状越偏离圆形。轴向系数分布在1.0～1.8之间，均值为1.28，轴向系数越大，砾石的长轴与短轴比值越大，条状性越明显。

图2 圆度频率（a）和轴向系数频率（b）分布直方图Fig.2 Distribution histogram of(a)roundness frequency and(b)axial coefficient frequency

1.3 砂石混合体的二重分形结构模型

Tyler 等[11]提出了基于分形理论的分形结构模型：

式中：r—颗粒粒径；

R—某一颗粒粒径；

MT—总质量；

RL—最大颗粒尺寸；

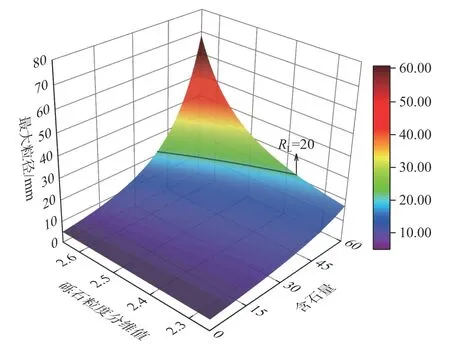
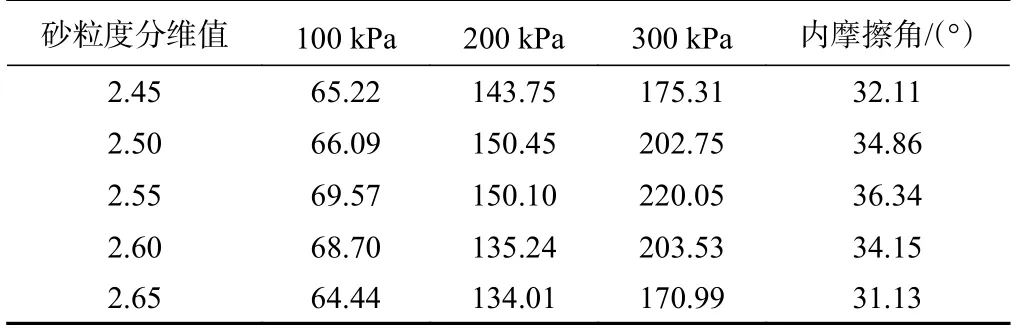
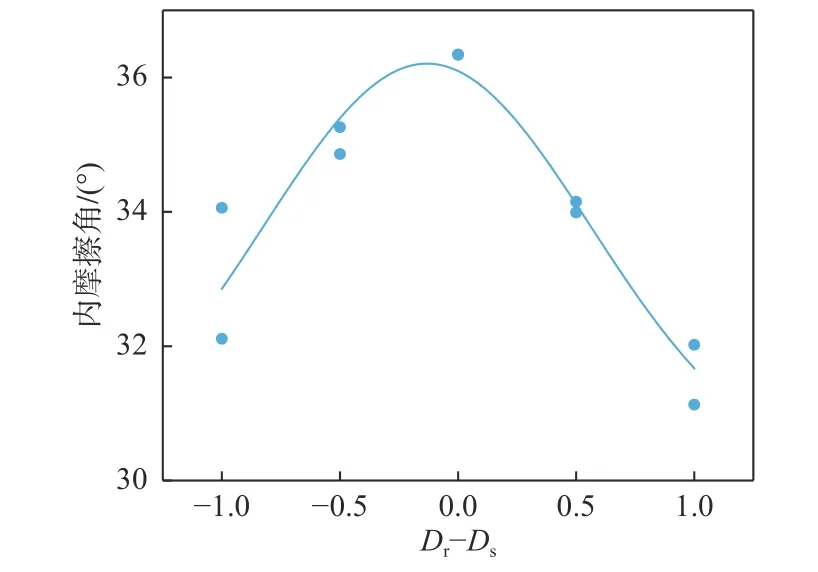
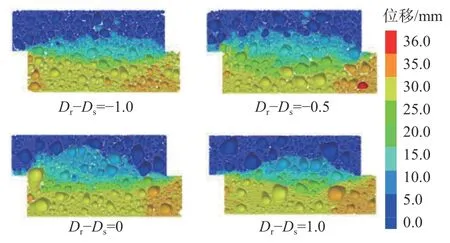
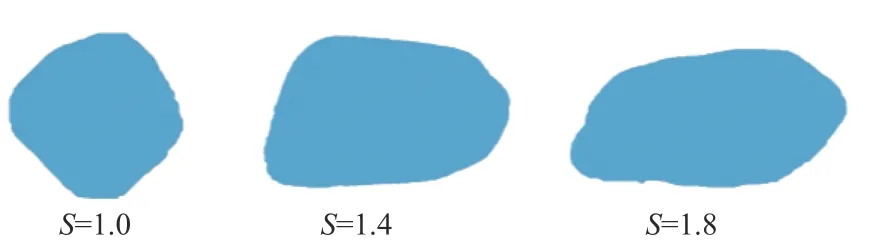
M(r

D—粒度分维值。

根据式（4）得出，如果在双对数坐标下lg[M(r

砂石混合体的粒度分布具有良好的分形结构，但是由于其复杂的颗粒组成，通常具有多重分维。本文结合砂石混合体的组成以及土石阈值构建二重分形结构模型:

式中：Ds—砂粒度分维值；

Dr—砾石粒度分维值；

RS/RT—土石阈值。

土石阈值，即“土”和“石”的界限粒径，本文结合以前学者的研究结果[12−13]，选取5 mm 作为砂和砾石的界限粒径。令式（5）中R=RS/RT即可确定砾石的最大粒径，公式如下[14]：

式中：P—含石量。

徐文杰等[15]指出含石量在25%～75%之间时，岩土体的强度取决于其中的“土体”与“块石”，其力学强度是两者相互作用的共同反映。含石量在这范围之外，整体的强度会主要取决于“土体”或者“块石”。为了分别研究砂和砾石级配变化对土石混合体强度的影响，需考虑两者共同作用，因此本文选取含石量为50%。

根据式（6）得出最大粒径、含石量和砾石粒度分维值的关系（图3），可以看出：随着含石量和砾石粒度分维值的增加，最大粒径变大；最大粒径保持不变时，砾石粒度分维值的增加，会导致含石量减少，两者关系曲线呈近似抛物线形状。

图3 最大粒径、含石量和砾石粒度分维值的关系Fig.3 Relationship among the maximum grain size,rock content and fractal dimension of gravel size

在确定含石量和土石阈值后即可根据不同粒度分维值确定砂石混合体的完整级配分布。首先需要确定每组粒径区间，取区间的粒径上限为该组粒径，并且粒组按粒径由大到小的顺序，即第1 个粒组的粒径为砾石最大粒径，则第i个粒组含量占总试样的百分数：

式中：R(i)—砾石第i组粒径上限。

将粒度分维值Dr或Ds代入式（7）就可确定不同粒度分维值下砂石混合体的试样级配。

2 基于PFC 的直剪试验模拟

2.1 直剪试验模拟流程

（1）剪切盒建立：砂和砾石颗粒单元均需要在剪切盒内生成。剪切盒尺寸和室内大型直剪试验截面一致，为300 mm×150 mm。模拟过程中剪切盒被认为是刚性体，剪切盒的刚度需大于砂和砾石的刚度，保证颗粒不飞出，并且避免模型内部产生较大初始接触力。通过试算，本文剪切盒刚度选取为1×1010N/m 。

（2）试样生成：砂采用ball 模拟，砾石采用前述构建的颗粒簇模板生成，接触模型采取线性接触模型。颗粒级配利用确定的二重分形结构模型，计算每个粒组需要生成颗粒的数量，并采用粒径扩大法生成特定级配的试样。需要注意的是：如果颗粒大小按照1∶1 的比例进行模拟，会对计算机提出较高要求，造成效率的降低。本文通过试算，设置颗粒放大系数为1.6，并忽略0.5 mm 以下颗粒，减少生成颗粒的数量，从而平衡PFC 模拟的精度和效率。

（3）施加竖向荷载：颗粒流软件中墙体无法直接施加力的作用，需要利用墙体的伺服机制，即在每一时步调整墙体的速度来控制墙体的受力大小。通过施加竖向荷载形成均匀试样，待稳定后，便可进行试样剪切。本文选取的主要正应力为100，200，300 kPa。

（4）试样剪切：剪切过程中维持上剪切盒不动，下剪切盒以一定速度向右移动，当剪切位移达到30 mm时停止剪切。剪切过程中监测剪应力和剪切位移的变化，记录数据。

2.2 细观参数标定

PFC 中颗粒的细观参数不能直接通过宏观参数获得，需要通过室内试验获取应力-应变曲线，并通过不断改变细观参数，使得数值模拟的结果与试验结果相近，完成细观参数的标定。本文采用Geotest S2450 型摩擦剪切仪进行直剪试验，砾石和粗砂作为试验材料。

由于砂石混合体参数较多，因此本文首先通过对单一砂进行直剪试验，获取砂的细观参数。并以此为基准进行砂石混合体直剪试验，完成其余参数的标定。经过大量参数试算，最终模拟曲线和实际试验曲线良好（图4），具体参数见表1。

表1 基于离散元模拟的直剪试验主要计算参数Table 1 Main computational parameters in DEM simulation of direct shear

图4 砂（a）和砂石混合体（b）剪应力-剪切位移模拟和实际试验结果对比曲线Fig.4 Shear stress-shear displacement comparison curve between the simulation and actual test results of(a)sand and(b)sand-gravel mixture

2.3 剪应力-剪切位移曲线特征分析

砂石混合体的抗剪强度明显高于单一砂时的抗剪强度。随着正应力从100 kPa 增加至300 kPa，颗粒间受到挤压排列更加紧密，剪应力逐渐增加。不同正应力下剪应力-剪切位移曲线呈明显的非线性特征，可分为3 个阶段[16]：线弹性阶段、初始屈服阶段以及应变硬化阶段，剪切过程中没有出现明显的峰值。

3 砂石混合体直剪试验结果分析

3.1 粒度分维值的影响分析

砂石混合体的抗剪强度分别受砂粒度分维值和砾石粒度分维值影响。为单独研究砾石粒度分维值的影响，采用控制变量法进行研究，首先保持砂的粒度分维值为2.55 不变，砾石的粒度分维值分别取：

2.45，2 .50，2.55，2.60，2.65。

砂石混合体的粒度分布曲线按照前文构建的二重分形结构模型计算，图5 为砂石混合体级配示意图，为了方便观察仅列出3 条典型曲线（下同），可以看出随着Dr增大，最大粒径也增大，在Dr=2.65 时，最大粒径达到32.23 mm。

图5 不同砾石粒度分维值的级配曲线Fig.5 Grading curves of fractal dimension of different gravel sizes

图6 是相应的剪应力-剪切位移曲线，采用了逐步平均法进行平滑，可以发现3 条曲线都近似呈应变硬化型，在Dr=2.55 时，曲线末尾其剪应力上升趋势还十分明显。抗剪强度与砾石的粒度分维值不是简单的线性变化，Dr为2.55 时抗剪强度最大，其值为220.05 kPa，而在Dr=2.45 和2.65 时，其值分别为196.07 kPa 和195.48 kPa，均明显小于Dr=2.55 的抗剪强度。

图6 300 kPa 正应力下不同Dr 剪应力-剪切位移曲线Fig.6 Shear stress-shear displacement curves of different Dr under the normal stress of 300 kPa

依据摩尔库伦准则τ=σtanφ+c，可以进行抗剪强度参数的计算。砂石混合体由砂和砾石组成，两者的黏聚力非常小，所以本文不考虑黏聚力，取值为0 MPa，此时抗剪强度主要由内摩擦角产生（表2）。

表2 不同砾石粒度分维值在直剪试验中获取的相关参数Table 2 Correlation parameters of fractal dimension of different gravel sizes obtained in the direct shear test

采用同样方法研究砂粒度分维值的影响，保持砾石的粒度分维值为2.55 不变，改变砂的粒度分维值，最终得出不同正应力下抗剪强度及内摩擦角的变化（表3）。

表3 不同砂粒度分维值在直剪试验中获取的相关参数Table 3 Relevant parameters obtained in the direct shear test of the fractal dimension of different sand particle sizes

为了方便观察，以砂、砾石粒度分维差值作为指标进行分析（图7），明显看出内摩擦角与Dr、Ds不是简单的线性变化，而是呈现先增大后减小的趋势。随着砂、砾石粒度分维值的接近，内摩擦角逐渐增加，当Dr−Ds=0 即砂石混合体具有单一分维时，内摩擦角达到最高值36.34°。

图7 粒度分维差值与内摩擦角关系Fig.7 Relationship between the difference in particle size fractal dimension and the angle of internal friction

为了探究影响原因，通过PFC 绘制出剪切结束时颗粒位移图（图8），颗粒的位移主要由两部分造成：第一部分是由下剪切盒的移动造成的，剪切过程中，上剪切盒保持不动，下剪切盒向右移动了30 mm；第二部分是由于剪切过程中颗粒的相互错动造成的位移。剪切盒的右下角颗粒位移最大，有的超过了30 mm，这主要是由于剪切过程中颗粒的移动并不能与剪切盒同步，在短时间里颗粒右侧形成一段空隙，使其变得较为松散，颗粒接触减少，易产生错动位移。由于上剪切盒在剪切过程中没有移动，位移主要由颗粒之间相互作用影响，因此具体分析上剪切盒颗粒位移。分析10～15 mm 剪切带附近的颗粒位移可以看出，随着砂、砾石粒度分维值的接近，10～15 mm 位移的颗粒范围在不断扩大，未受影响的颗粒范围在减少。这说明随着砂、砾石粒度分维值的接近，可观察到颗粒排列的越紧密，因剪切盒移动产生的相互错动越明显，颗粒位移增加，导致抗剪强度增加，内摩擦角也增大。

图8 不同粒度分维差值的位移变化图Fig.8 Displacement change diagram of difference of different fractal dimensions

综上，当砂、砾石粒度分维值越接近，其抗剪强度越大，内摩擦角也相应越大。当两者相等时，即砂石混合体只具有单一分维，此时试样的均一性达到最好，具有最大的抗剪强度和内摩擦角。

3.2 轴向系数的影响分析

由于本文在边界平滑和颗粒填充算法中对砾石细部边界信息有所缺失，因此只对轴向系数进行具体分析。从砾石数据库选取颗粒圆度大致相同，轴向系数分别为1.0，1.4，1.8 的砾石进行模拟（图9）。为了减少其他方面影响，模拟时选取单一颗粒形状。由图9可以看出，轴向系数越大，颗粒条状性越明显，反之，越接近于圆形。

图9 不同轴向系数的砾石Fig.9 Gravel with different axial coefficients

对不同正应力得到的剪应力峰值进行线性拟合（图10），可以发现拟合相关系数R2都在0.99 以上（表4），表明通过摩尔库伦强度准则得到的内摩擦角比较可靠。随着轴向系数的增加，抗剪强度和内摩擦角逐渐增加，S=1.8 时内摩擦角达到最高值35.92°。产生这种情况主要是因为，砾石轴向系数越大，颗粒条状性越明显，从而有更多机会接触不同颗粒，颗粒的抗转动能力也得到了提高[17]。

表4 不同轴向系数在直剪试验中获取的强度参数Table 4 Strength parameters obtained in direct shear test with different axial coefficients

图10 不同轴向系数下剪应力峰值-正应力曲线Fig.10 Shear stress peak-normal stress curve under different axial coefficients

由图11 可以发现，颗粒在剪切面附近旋转角度偏高，并且越靠近左右边缘旋转角度越大。由于颗粒移动的延迟性以及不均匀导致剪切盒右下方砾石周围的接触数量也明显降低。

图11 砾石颗粒旋转角度及周围接触示意图Fig.11 Schematic diagram of rotation angle and surrounding contact of gravel particles

为具体了解相关变化，通过Fish 语言获取300 kPa正应力下砾石和周围颗粒的接触数量以及旋转角度（表5）。由表5 可以看出，随着轴向系数从1.0 至1.8变化，接触数量从1 581 增加至1 742，砾石的平均旋转角度从9.43°减少至6.42°。这说明随着轴向系数增加，砾石颗粒的条状性越强，和其它颗粒的接触可能性越多，也导致其在旋转时遇到的阻力越多，抗转动能力较强，在剪切过程中旋转的角度总体上偏低，从而导致抗剪强度提高。

表5 不同轴向系数下砾石接触数量和旋转角度Table 5 Gravel contact number and rotation angle under different axial coefficients

4 结论

（1）利用数字图像处理技术能够自动化完成砾石真实图像至颗粒簇模板的转换，构建砾石的形状数据库，并可对轴向系数、圆度等形状参数进行分析。

（2）基于分形理论建立了砂石混合体的二重分形结构模型，得出完整的粒度曲线。土石阈值一定时，砂石混合体的最大粒径随含石量、砾石粒度分维值的增加而变大。最大粒径保持不变时，砾石粒度分维值的增加，会导致含石量减少，两者关系曲线呈近似抛物线形状。

（3）砂、砾石粒度分维值越接近，抗剪强度越大，内摩擦角也相应越大，当两者相等时，即砂石混合体只具有单一分维时，此时试样的均一性达到最好，具有最大的抗剪强度和内摩擦角。

（4）轴向系数S是形容砾石形状的一个重要参数，其分布在1.0～1.8 之间。随着轴向系数S的增加，砾石条状性越强，在直剪试验中抗转动能力越强、与周围接触可能性越大，导致抗剪强度和内摩擦角不断增加。