浅谈不定积分的学习方法

张倩倩

（湖北大学知行学院 湖北·武汉 430011）

1 不定积分的重要性

在整个高等数学知识点中主要可分为一元函数积分学及应用和多元函数积分学及应用，其中多元函数积分可最终转化为一元函数多次积分，一元函数积分又根据积分区间分为不定积分、定积分、反常积分，定积分的求解方法中有一种是先当成不定积分求出原函数再利用牛顿-莱布尼茨公式求出最终数值，反常积分在求解题目过程中有时也需要先当成不定积分求出原函数，再利用牛顿-莱布尼茨公式和极限最终求出结果。所以针对整个积分学求解的方法来说，我们可重点探究不定积分的求解方法。

2 不定积分的三种求解方法

相比较而言，这三种方法中，直接积分法是最简单的也是最基础的，无论是换元法还是分部法在做题过程中都要用到直接法，它们不是相互独立的关系，而是你中有我，我中有你的关系。在一道题中，这三种方法可能同时运用才能解出最终的结果。所以，这三种方法需要同时掌握，而不是只掌握一种，同时这也是很多同学认识不清的地方。在这几年的教学过程中，发现大家对于积分的方法使用不太了解，每次做题都是盲猜。为了学生更好的掌握积分方法，我根据自己的做题的思路和学生的反馈总结出按照被积函数的类型可大致判定优先使用积分的方法。

3 三种方法的优先使用顺序

被积函数中不含有对数函数和反三角函数。步骤：（1）被积函数是基本初等函数（即幂函数、指数函数、三角函数）的线性组合，则优先使用直接积分法。（2）若被积函数是两类不同函数相乘的形式，则优先使用分部积分法，见例1。（3）若被积函数中含有复合函数，则优先使用换元积分法，见例2和例3。

求不出来结果。

被积函数中若只是两个函数（指数函数和三角函数）相乘时，如不定积分，要使用两次分部积分法。切记“从一而终，不可始乱终弃”。从一而终说的是遇到需多次使用分部积分方法的题时，第一次用分部积分法时无论选取指数函数还是三角函数，只要第二次使用分部积分法时在选取和时与第一次使用分部积分法选取的是同一种类型，则能得到最终结果，否则，无法得到正确结果。不但在做题过程中要秉承这一原则，在生活中也要有这样的意识，这也是数学与文学、哲学的结合，在课堂教学过程中不但要教授知识，也要陶冶学生的情操，培养应用型人才，把数学方法应用到其他学科和人生这个大学科中。

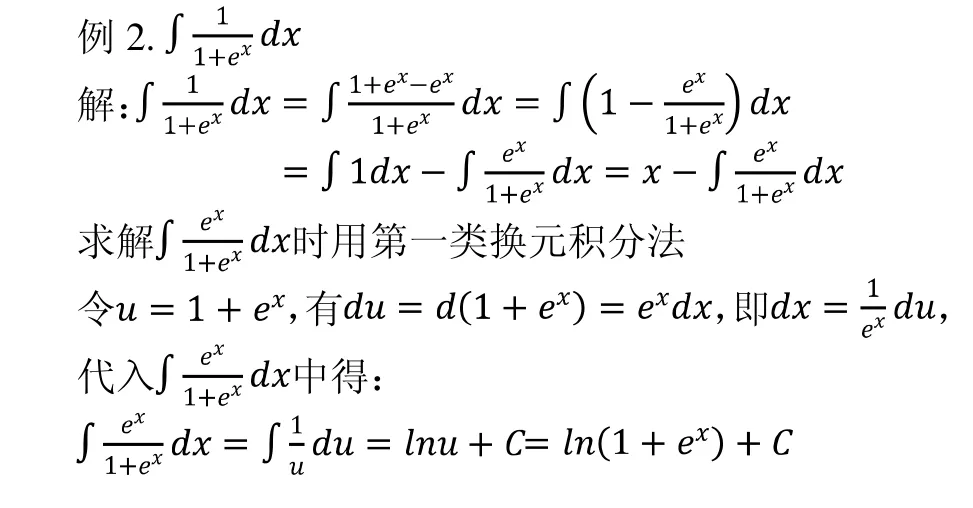
换元积分法也是一种比较重要的方法，核心步骤在于第一步要找到换元的部分和最后一步再换回原来的积分变量。在上述解题过程中，用到了“凑”，把原本的被积函数凑成可以使用直接积分法的形式。