许东沟矿下盘岩体边坡能量突变分析

白梦月 常来山 桑晓晓 寇明清

（1.辽宁科技大学矿业工程学院，辽宁 鞍山 114051；2.辽宁科技大学土木工程学院，辽宁 鞍山 114051；3.岫岩满族自治县水利事务服务中心，辽宁 鞍山 114582）

0 引言

边坡失稳是露天开采工程中时常遇到的重大问题，对露天矿的安全生产和企业经济效益有着直接影响。为减少边坡失稳造成的灾害与事故，国内外研究者对此进行了大量的分析和研究。极限平衡法以其简单实用的特点在岩土边坡稳定性评价中得到了广泛应用，且成为相应评价分析标准的主要方法。但由于它的基本假定是岩体为刚性体，不考虑岩体的形变特征，它的缺点也比较明显。许多学者在边坡稳定性分析计算方法方面进行了大量卓有成效的探讨，如Wang等［1］提出了一种基于位移统计的离散元建模方法（DSDM），与抗剪强度折减法（SRM）相结合，能够有效地分析具有潜在滑动面的节理边坡的稳定性。张小勇等［2］通过建立离散元模型，分析承张高速某顺层页岩边坡工程稳定状态，并对其失稳过程进行研究。Yang［3］依托有限差分分析软件FLAC3D，介绍了关于抗剪强度折减法和边坡稳定性数值模拟评价的基本原理和方法。Zabuski［4］利用弹塑性有限差分法研究了空间与平面分析边坡几何形态对稳定性的影响。20世纪70年代，Thom首次提出了突变理论，并在具有突变破坏特性的边坡稳定性方面得到应用并被推广，被用来分析边坡失稳破坏的问题。Dai等［5］依据尖点突变理论开发了自动搜索边坡安全系数的计算程序，并用于确定边坡稳定性状态。在尖点突变理论的基础上结合有限元强度折减法，娄一青和宋鑫华等［6，7］给出了判断边坡失稳与否的条件。岳建伟等［8］利用尖点突变模型推导出滑面与失稳点在不同应变状态下的边坡滑体高度的关系式，宋盛渊等［9］利用突变级数分别对边坡的稳定状态和滑坡危险性进行评价分析，刘海［10］结合损伤力学与突变理论知识针对岩质边坡的失稳破坏机理进行了研究。

许东沟露天矿是鞍千矿业的一个主要采场，一期境界开采时曾发生多次边坡变形破坏，二期境界设计时需重点进行境界边坡的稳定性评价，探讨多种边坡稳定性评价方法，对边坡优化设计意义重大。

1 能量突变基本理论

1.1 突变理论概述

突变理论主要是寻找系统发生质变的奇异点。即描述系统在自然界处于稳定或非稳定状态时，存在一组参数能够描绘系统当前状态。当系统处于稳定状态下，其对应函数存在唯一满足条件的极值。反之，若函数有多个极值存在，则系统处于非稳定状态；若该参数经过微小扰动或调整后系统恢复并进入新的稳定状态，该过程即为突变过程。而边坡的失稳过程正是从稳定到突变、由量变到质变的一个非线性过程，因此，突变理论在边坡工程中有着广泛的应用并成为边坡稳定性的一个评价方法。Thom R用4个控制变量总结了7种突变模型：折迭型、尖点型、燕尾型、蝴蝶型、椭圆脐型、双曲脐型和抛物脐型。

1.2 尖点突变理论

突变理论作为一种非线性科学，用定量分析方法描述岩石工程中边坡稳定性等不可逆的非线性系统临界灾变现象，已被广大学者接受并应用于工程实际中。通过对边坡岩体进行强度折减可以获得对应强度的能量场序列，可通过5次泰勒级数展开式来拟合表示不同边坡能量（重力势能、动能、弹性应变能及耗散能）与强度折减系数的关系，并将其转化为尖点突变模型的势函数，通过计算得到的分叉集Δ判断边坡所处的状态。

尖点突变模型的势函数标准形式为

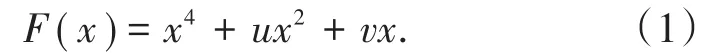
能够满足奇点集方程F″（x）的点周围平衡位置数目并不一样，这些点被叫做突变点（又叫奇异点）。系统的状态变化分2种情况：渐变和突变，也就是量变和质变。

势函数的一阶导数和二阶导数均等于零时，根据控制变量u和v，可计算得到的分叉集Δ判断边坡所处的状态：

1.3 岩体系统或单元体能量计算

依据建成的数值模型，选择任意一个单元体作为能量计算研究的对象。

单元体重力势能密度ug可由单元体材料密度ρ、单元体到基准面高度h和重力加速度g计算：

单元体动能密度uk可根据单元体运动速度v计算：

单元体弹性应变能密度uε可根据单元体主应力σ1、σ2和σ3计算：

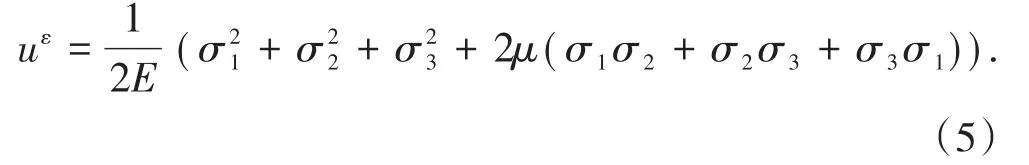
对于封闭的岩体系统，当岩体破坏时，一部分岩体由弹性状态转变为塑性流动状态，弹性能耗散掉，可记为耗散能，由封闭系统的能量守恒原理得到。边坡岩体向下滑动破坏时，表现为某区域岩体的弹性能产生突变性减小，重力势能降低，动能增大，耗散能增大。

2 FLAC建模

许东沟露天矿采场二期设计最大开采深度为-348 m，总体边坡角43.6°～46.9°，根据许东沟采区东帮边坡5 900、6 100、6 300、6 500四个地质剖面建立三维FLAC模拟计算的力学模型，如图1和图2所示。

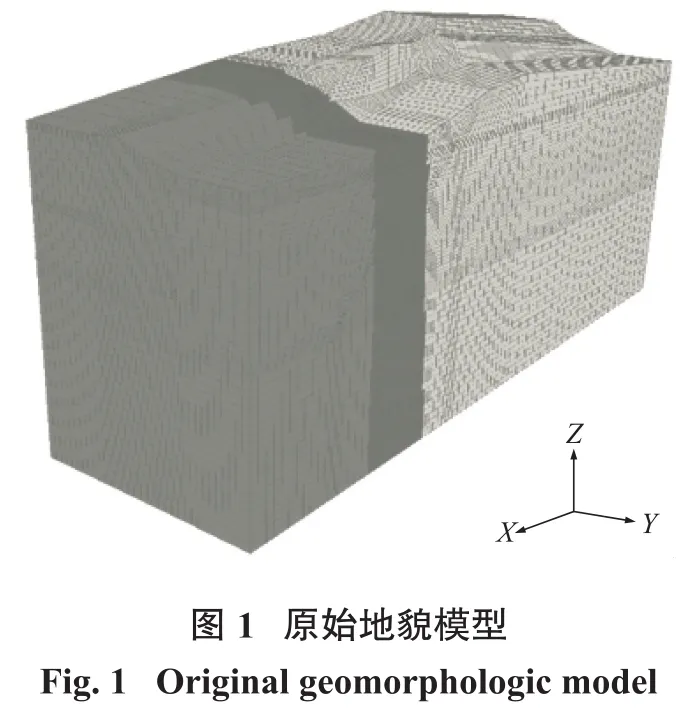
上部岩体为块状结构的混合岩，下部为磁铁石英岩（铁矿体），均采用摩尔—库伦本构模型（Mohr-Coulomb）进行建模，中间部分为顺倾层状结构的绿泥石英片岩，采用节理化本构模型（Ubiquitous）进行模拟。完成自重条件下初始应力场运算后，按二期境界+48 m、-48 m、-204 m及-348 m水平共4步进行模拟开挖。

3 边坡稳定性的能量突变分析

3.1 能量突变分析方法

应用FLAC应力分析平台（或其他软件）进行模拟开挖，计算统计待分析区域的岩体能量密度（重力势能、动能、弹性应变能及耗散能），作为下一步分析的零点。

针对各种采场开挖深度的岩体边坡，应用强度折减法进行强度折减重置，进行一定步数的FLAC模拟计算，选取一系列的折减系数进行反复计算；并统计待分析区域的岩体能量密度的变化情况（增量或减量）。

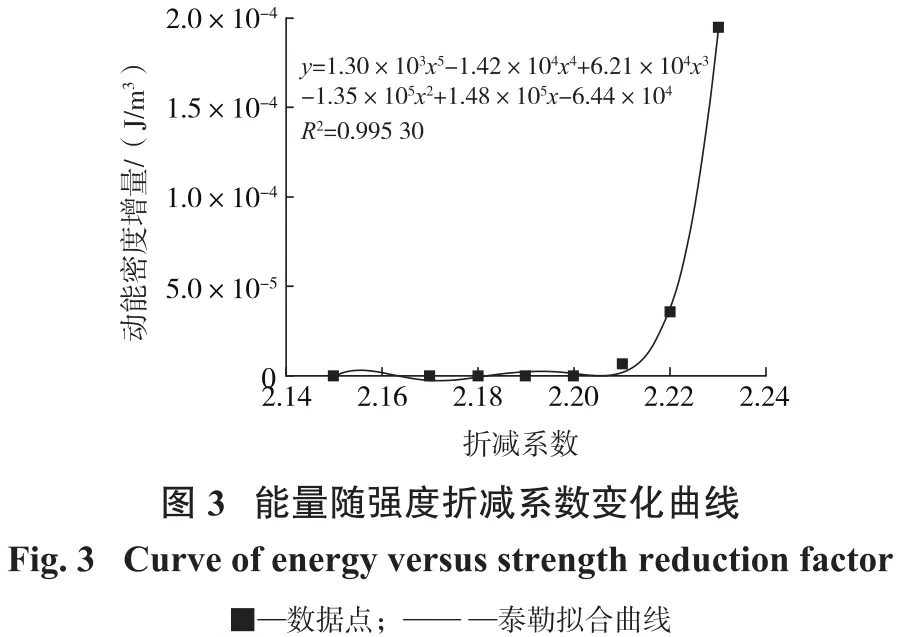
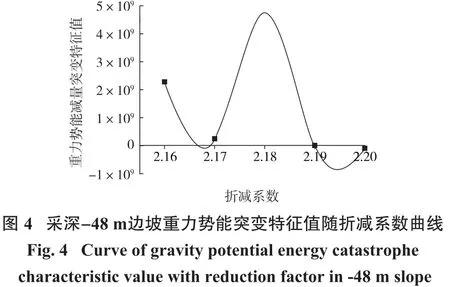
应用5次泰勒级数展开式来拟合边坡岩体能量与强度折减系数F的关系（图3），并将其转化为尖点突变模型的势函数，以分叉集Δ判断边坡所处的状态（图4）。当特征值Δ＜0时，表示岩体边坡的能量值随强度折减系数的变化超出分叉集区域，边坡发生失稳；特征值Δ＞0，边坡处于稳定状态。边坡的安全系数可确定为Δ＜0和Δ＞0对应的强度折减系数的中间值。

3.2 能量统计区域形状影响

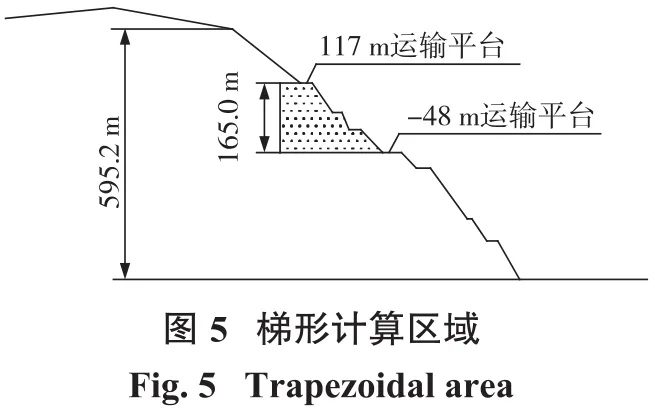
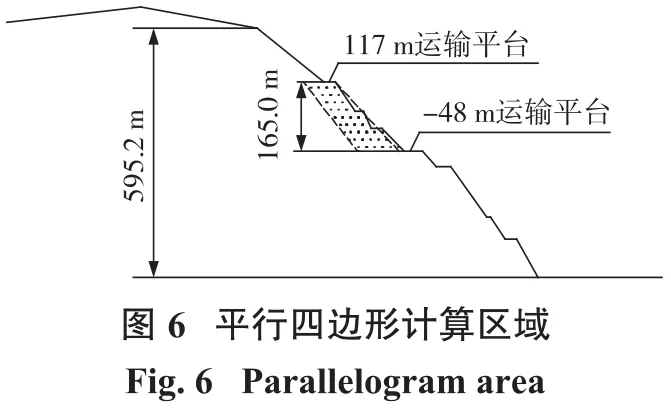
计算分析局部边坡的稳定性，很自然涉及到能量统计区域是选择梯形还是平行四边形问题。如图5和图6所示，经计算分析对比，二者统计得到的能量密度数值虽略有变化，但突变点一致。

3.3 许东沟露天矿稳定性分析

FLAC模拟计算是基于动态松弛算法的大变形分析，可以得到一定时步后的单元体速度和坐标位置，即可以计算得到单元体的动能和重力势能，具体数值大小当然与时步的选择相关，但不影响突变点的分析计算。对于耗散能而言，由于计算的局部区域与周围岩体有能量交换，其值包含在耗散能之内，影响其大小，但不影响突变分析

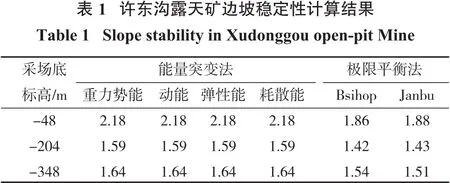
重力势能、动能、弹性应变能及耗散能的突变分析得到的边坡安全系数基本相同，与极限平衡法的Bishop和Janbu法对比，数值略所差异，均大于极限平衡法计算所得的边坡安全系数。

采深到-48 m时，边坡岩体全部由混合岩构成，边坡安全系数高达2.18，初期开挖时边坡较为稳定；采深到-204 m时，绿泥石英片岩在边坡出露，安全系数下降到1.59；而下部边坡由强度较高的磁铁石英岩（铁矿体）构成，边坡高度虽然增加，安全系数并未下降，最终边坡安全系数为1.64。

4 结语

边坡稳定性计算一直以极限平衡法为主，尽管有不考虑岩土体变形的主要理论缺陷，虽然后来的研究采用辅之以数值分析的单元安全度计算的策略，但总体上其效果尚未改观。数值模拟、强度折减和能量突变相结合，可从根本上改变稳定性分析计算的现状，是值得深入研究的一种计算体系。