齿间非线性单级平行轴轮系的动态特性研究

周新涛，刘引涛，崔亚辉

1陕西工业职业技术学院机械工程学院 陕西咸阳 712000

2西安理工大学机械与精密仪器工程学院 陕西西安 710048

齿轮作为机械传动系统常用的基础件之一，其性能直接影响到机械系统或机械设备的整体性能[1]。齿轮在实际应用中，由于制造误差、安装误差、轴承游隙以及齿轮系统构件受力变形等因素的存在，会使相互啮合的齿轮理论的轴心线产生平行度误差[2-4]。这些因素与轮齿的时变刚度、齿面摩擦和稳态传动误差等因素在齿轮运行的过程中，将会产生强非线性特性，使齿轮系统的动力学和运动学特性变得极其复杂，从而影响轮系动态特性[5-6]。

传统的动力建模方法均是采用简化或等效的方法，将齿间非线性因素的数学模型进行简化处理，难以建立齿间系统非线性因素的精确模型。经简化后处理的非线性因素在系统动力学中起到的作用将会被掩盖或忽略掉，致使轮系真实的动力学行为严重偏离实际情况，而且不能准确的反映轮系真实的动态特性。

笔者以结构简单的单级平行轴轮系为研究对象，根据齿间系统非线性因素的产生机理，再结合键合图建模法的基本原理和优势，建立了齿间系统的时变啮合刚度、齿面摩擦和稳态传动误差 3 种非线性因素的键合图模型。然后，采用键合图法建立了单级平行轴轮系含上述 3 种非线性因素的键合图模型。最后，通过数值仿真分析，研究了单级平行轴轮系在非线性状态下系统动态特性的动力学规律。

1 键合图法

1.1 图元

键合图法利用强大的图元库和灵活的建模方式，能模拟出各种类型能量系统中线性或非线性的相关特性。传统单一能域的建模与分析方法，就难以达到这种显著效果。键合图的基本图元如表 1 所列。

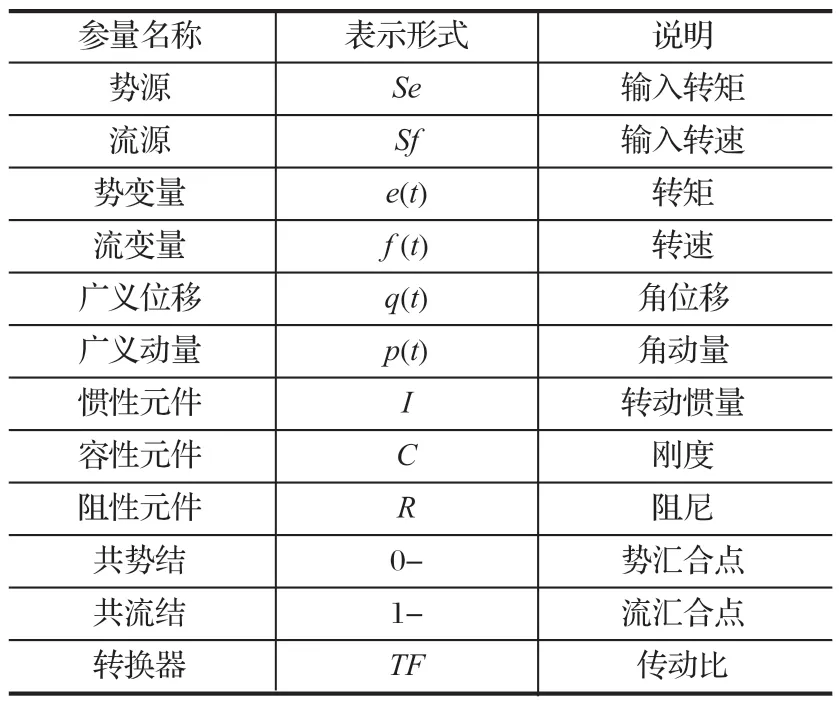
表1 键合图的基本图元Tab.1 Basic primitives of bond graph

1.2 建模规则

齿轮机构的建模规则要符合回转机械系统的特征。其建模规则如下所示[7]。

（1）根据轮系系统的性质，为轮系中每个绝对速度和相对速度建立 1 个 1-结；

（2）在每 2 个 1-结间插入 1 个 0-结，也可以在 2个 1-结之间插入 TF 键元；

（3）将惯性元件和势源键，键接在对应的绝对速度 1-结上；

（4）将轮系的势源、流源或阻性元件以及容性元件键接在对应的速度 1-结上；

（5）根据轮系中功率流动的方向，确定各图元的因果关系；

（6）根据键合图简化计算规则，将轮系的模拟拓扑图进行简化。

1.3 单级平行轴轮系的动力学模型

一对相互啮合的齿轮是这个系统中最小的传动单元，即单级平行轴轮系。单级平行轴轮系的键合图模型是以这组最小传动单元为载体，其动力学模型的如图 1 所示。O1为主动齿轮，O2从动齿轮；x1（t）、x2（t）分别为轮齿啮合线上的相对位移；T1、T2分别为输入、输出转矩；θ1、θ2分别为主、从动齿轮的角位移；k为轮齿啮合刚度；C为轮齿啮合阻尼；J1、J2分别为主、从动齿轮的转动惯量；e（t）为轮齿综合啮合误差；R1、R2分别是为齿轮O1、O2的分度圆半径。

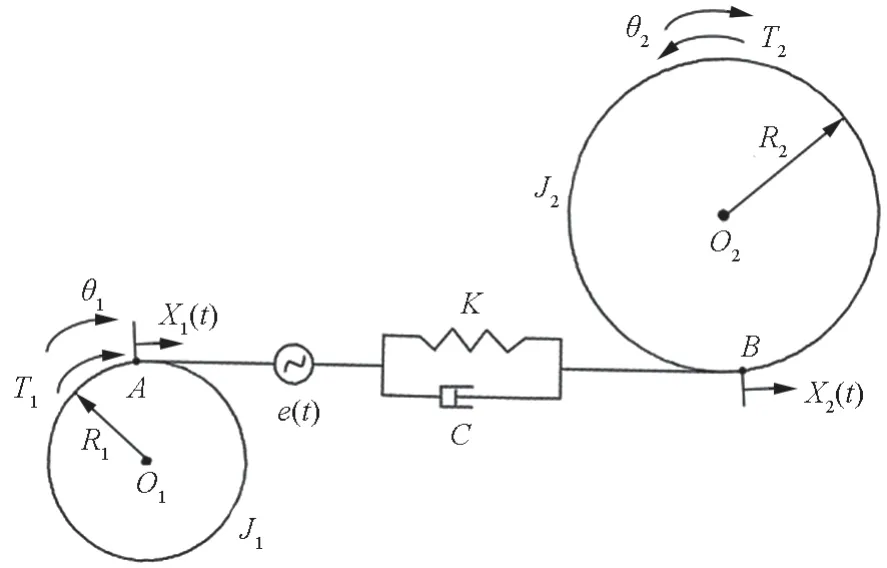
图1 单级平行轴轮系的动力学模型Fig.1 Dynamic model of single-stage parallel shaft gear train

2 齿间系统的键合图模型

2.1 时变啮合刚度

轮系啮合的时变刚度[8-9]

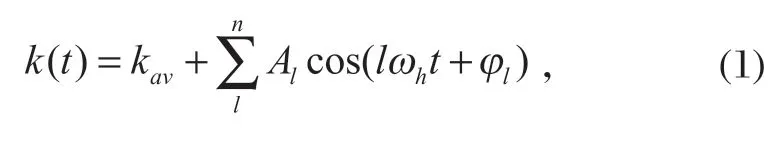
式中：kav为啮合刚度的平均值；l为谐波阶数；Al为在l阶时对应的幅值；ωh为轮齿的啮合频率；φl为l阶时对应的相位角。

根据轮齿时变啮合刚度理论和键合图建模机理，建立时变啮合刚度的键合图模型，如图 2 所示。图中，C1、C2和C3为模拟刚度的容性元件；µ1、µ2和µ3均为布尔开关，在同一时间段只能有一个起作用。

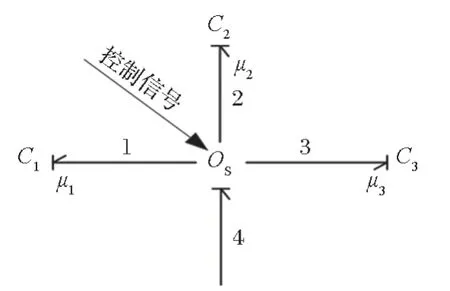
图2 时变刚度的键合图模型Fig.2 Bond graph model of time-varying stiffness

2.2 齿面摩擦

摩擦力在齿轮传动系统中消耗系统中的驱动能量，故在键合图建模时可将其简化成耗能元件 R。采用功率结型结构[10]（SPJ）法，用 0s-结和 SPJ 开关模拟齿面摩擦效应；采用 1s-结和 SPJ 开关模拟齿面摩擦力的方向与相对啮合速度之间的关系；摩擦因数µ采用可调阻性转换元件（Modulated Resistive，MR）模拟；FN为参量信号控制键。另外，该图中的变量µ1和µ2为 2 个相互排斥的布尔变量，在同一时间段内只能有一个变量被激活。因此，根据齿面摩擦理论和键合图建模法机理，建立齿面摩擦的键合图模型，如图 3 所示。

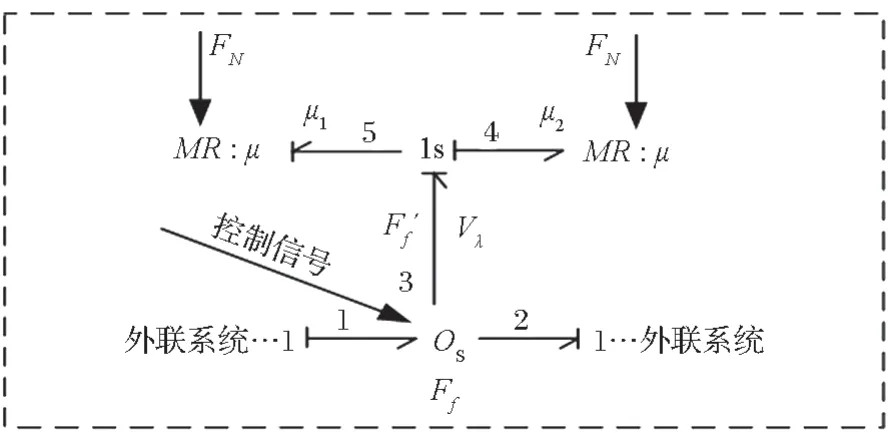
图3 齿面摩擦的键合图模型Fig.3 Bond graph model of tooth surface friction

2.3 稳态传动误差

齿轮在传动过程中有很多因素会导致产生传动误差，主要包括齿轮的制造误差和齿轮的安装误差。传动误差使轮系在传动过程中偏离理想位置，导致轮系出现振动或噪音。且会使轮系传动系统的工作状态变得复杂化，从而降低了轮系的使用寿命。传动误差在齿轮传动过程中，随着时间的变化而具有一定的周期性。当对轮系力学特性研究时，可将其投影到啮合线上，如传动误差函数[11]

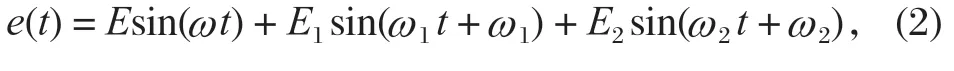
式中：E为齿频误差；E1、E2分别为齿轮O1、O2的安装误差；ϕ1、ϕ2分别为齿轮O1、O2安装误差的初相位；ω1、ω2分别为齿轮O1、O2的转动角速度。

E（t）是以位移激励的形式作用于轮系的传动系统中，e（t）的键合图模型，可用导数e（t）′作为流源Sfwc来模拟，

传动误差系统中引起的弹性变形，用容性元件C表示，接触阻尼用阻性元件R表示，其键合图模型如图 4 所示。

图4 稳态传动误差的键合图模型Fig.4 Bond graph model of steady-state transmission error

2.4 单级平行轴轮系的非线性动力学模型

根据文献 [12] 及变刚度、齿面摩擦和稳态传动误差等非线性因素的键合图模型，将其融合到平行轴齿轮传动系统中，从而建立该齿轮系统的键合图模型，如图 5 所示。

3 单级平行轴轮系的动力学仿真分析

3.1 仿真参数设置

根据图 5 所示的非线性键合图模型，按照仿真模型条件，得出如图 6 所示的仿真模型。图 6 中开关元件 1s、0s在键合图的模型库中无此类模拟元件，可采用 SIDOPS+语言编制开关元件 1s、0s的控制程序。其中，MR模拟齿面摩擦；Kc模拟时变啮合刚度；MSf模拟传动误差。另外，采用 4 阶变步长 Runge-Kutta 4 法的求解器，计算仿真模型的状态方程组。

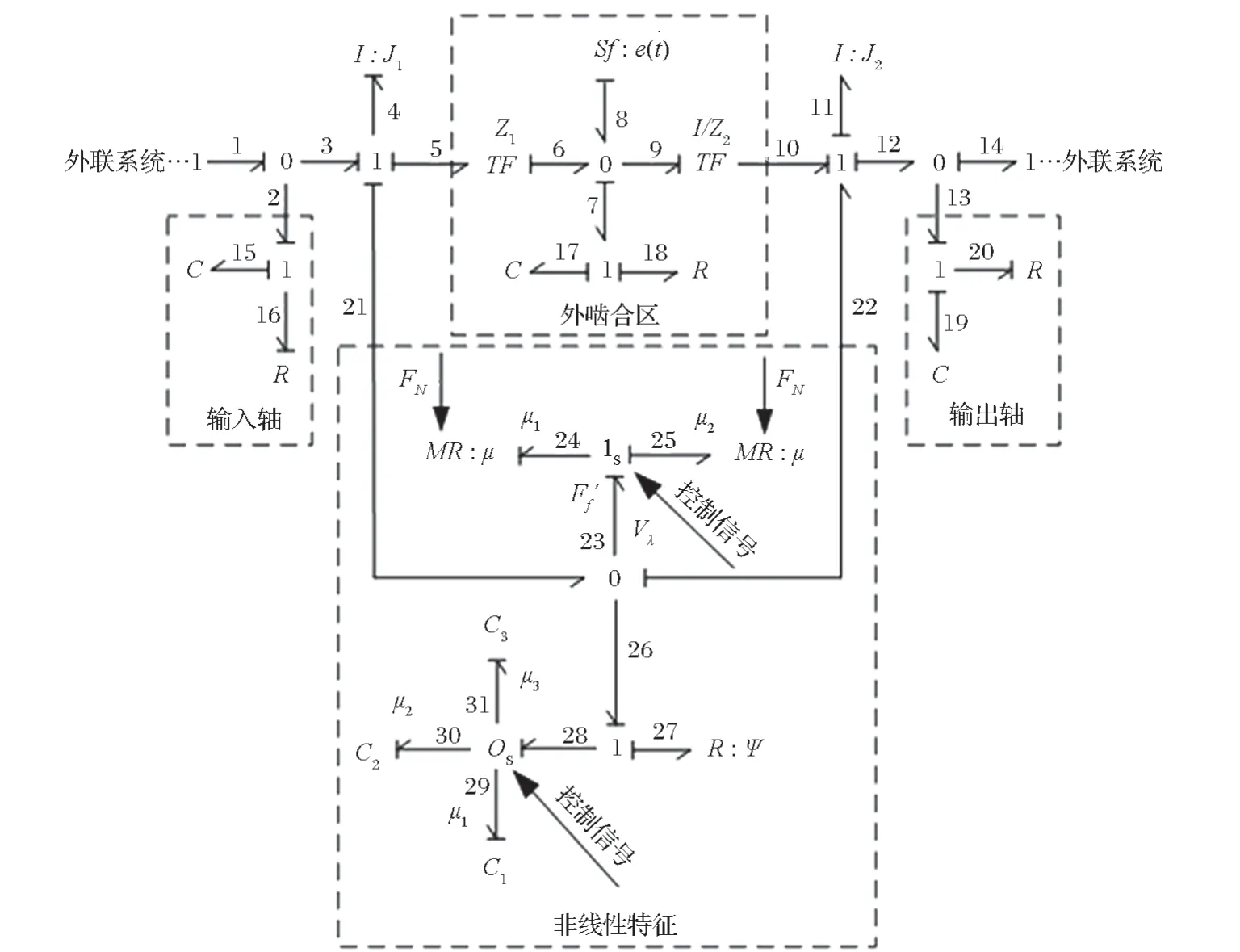
图5 平行轴轮系的非线性键合图模型Fig.5 Nonlinear bond graph model of parallel shaft gear train

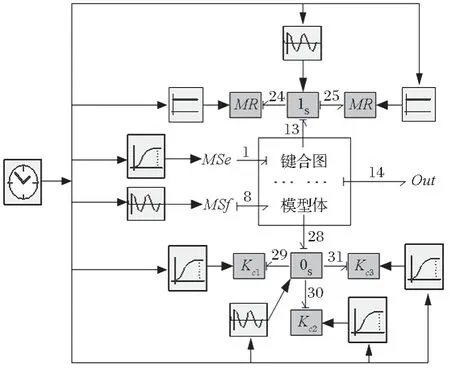
图6 单级平行轴轮系的非线性仿真模型Fig.6 Nonlinear simulation model of single-stage parallel shaft gear train

将仿真参数设置为[13]：齿数Z1＝16，Z2＝24；弹性模量E＝2.1×1011N/m2；泊松比µ＝0.3；惯性矩I1＝0.041 kg/m2，I2＝0.079 kg/m2；扭转刚度K＝2×108N/m；支撑阻尼Cv＝1 800 N·s·m-1；啮合阻尼Cg＝2 000 N·s·m-1；输入力矩TI＝470 N·m；阻力矩TO＝320 N·m；稳态传动误差的导数e˙（t）=0.002 7 cos（28t+21pi）。

3.2 仿真结果及分析

单级平行轴轮系的极点-零点图如图 7 所示。由图 7 中可得出，系统的开环传递函数的 2 对极点和零点等于 0，则构成了偶极子而相互消除。同时，在该系统中在复平面 [S] 的右侧无极点、零点，故该系统的开环传递函数为非最小相位系统。另外，也说明系统闭环的极点都在复平面 [S] 的左侧，所有闭环极点都有负实部。当时间t→∞ 时，系统指数项和阻尼指数项分量都将快速趋于零，则系统是稳定的。系统最大超调量Mp＝1.186×10-6，上升时间tr＝4 416.96 ms，最终在调整时间内振荡 7 次趋于稳定。

图7 单级平行轴轮系的极点-零点图Fig.7 Pole-zero diagram of single-stage parallel shaft gear train

单级平行轴轮系的动态特性指标如图 8 所示。从图 8（a）可得出，系统的相位裕量γ（ωc）=-3.15×10-6deg＜0（3.26×10-11rad/s），幅值裕量Kg=-244 dB＜0（0.166 rad/s）。故此，根据博德图中的稳定裕量值可判断该系统稳定。图 8（b）所示的尼柯尔斯图纵轴是幅值的对数，横轴是相角，该图反映了幅值与相角的变化关系。图 8（b）也能进一步说明 P 型单元体在此种模拟工况下，其闭环系统是稳定的。由图 8（c）所示的尼奎斯特图中可得出，该系统的开环频率特性曲线不包围（-1，j0）点，且开环无右极点。同时，可从尼奎斯特图的局部放大图中得出，开环系统相图包围原点2 次。

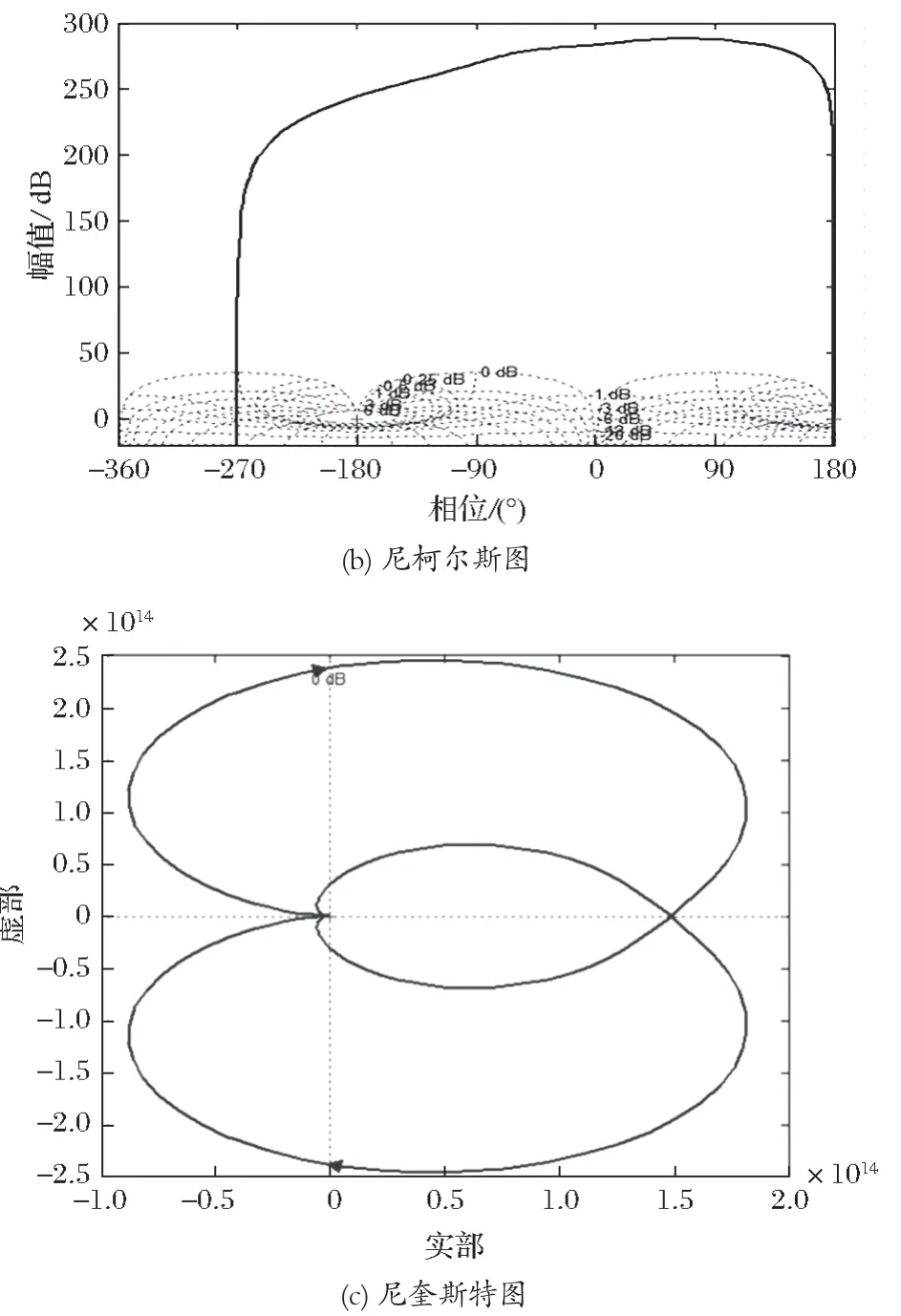
图8 单级平行轴轮系的动态特性指标Fig.8 Dynamic characteristic indexes of single-stage parallel shaft gear train

4 结论

通过单级平行轴轮系精确化的建模方法，建立了该齿轮系的键合图模型。考虑了齿间系统的非线性因素，如时变啮合刚度、齿面摩擦和稳态传动误差 3 种因素，并分别建立了键合图模型，研究非线性因素齿轮系统动态响应的影响情况。

（1）根据键合图建模法的建模原理和优势，总结出采用该法建立单级平行轴轮系的等效建模规则。

（2）研究了齿间系统的时变啮合刚度、齿面摩擦和稳态传动误差 3 种非线性因素的建模方法，并采用功率结型结构（SPJ）法，分别建立了非线性因素的键合图模型。

（3）采用键合图法，建立了单级平行轴轮系的非线性键合图模型。

（4）采用数值仿真法，得出了单级平行轴轮系的极点-零点图、博德图、尼柯尔斯图和尼奎斯特图 4个动态指标。可判断出单级平行轴轮系，在非线性状态下，其系统的动态稳定性较好。