改进启发算法在半导体生产调度中的应用研究

高 强，郭大权，李 飞，王 巍

(1.红塔辽宁烟草有限责任公司，辽宁 沈阳 110002；2.中国科学院沈阳自动化研究所，辽宁 沈阳 110016)

1 引言

现代企业正在通过大型设备实现持续，高速和自动化。重点放在高品质，低成本，准时交付和小批量订制生产。为提高竞争力，许多大型企业致力于开发可提高大型设备生产率、缩短运营间等待时间、节省材料和能源并能够降低生产成本的计算机集成制造系统(CIMS)。生产调度是CIMS的关键组成部分。其任务是确定不同工位的开始生产时间和完成时间，以便企业提高生产效率，实现产量的提升。

近年来，半导体行业的高速发展，吸引了许多研究人员的目光，很多研究机构都在提高生产效率的方面进行了深入的研究。本文研究了半导体生产的调度优化问题，针对半导体封装调度优化的问题提出了一种新的基于作业和资源动态优化的调度优化算法和解决方案。同时，通过建立阶段模型和优化算法解决了生产优化的问题，降低了问题的复杂度。本文充分结合半导体生产的特点，同时，基于现有生产调度理论与实际生产应用的差距较大，该项目是以半导体封装企业为实际研究对象，力争为企业提供可行的生产调度优化方案和实用的系统提高生产效率。

2 国内外研究现状

在过去几年中，提出了小型工厂生产计划过程的数学模型。半导体制造商正在越来越多地将多个芯片组装成一个封装，以最大化闪存的容量。通过关注瓶颈阶段，同时满足实际操作约束条件，找到半导体封装设施的良好时间表。

Tsen[1]等人研究了加工时间可控的单机调度问题，该问题的目标是最小化总延迟时间和压缩成本加权之和。建立了该问题的两种线性规划数学模型，提出一种净压缩收益算法(Net Benefit of Compression，NBC)并对该小规模车间调度问题进行求解。Kayvanfar[2，3]等人延续了TSeng的工作，并提出了一种净压缩及净扩展收益算法(Net Benefit Compression-Net Benefit Expansion，NBC-NBE)求解该类问题。Yin和Wang[4]采用了启发式算法来求解加工时间可控和学习效应的单机调度问题。该问题的目标是最小化完工时间、总完工时间和完工时间的绝对差异等成本函数。翟颖妮[5]等利用正交设计，识别生产过程中的瓶颈，对生产调度具有一定指导意义。但是结果的准确性依赖构造的正交表，该方法就不适用于多机器的瓶颈识别问题。ZHANG[6，7]通过放松调度问题分析机器的唯一性占用约束，得到一个新的优化模型，提出了一种基于约束转换的作业车间先验瓶颈识别方法。但是新的优化模型也属于复杂的组合优化问题，求解过程复杂，因此不适用于大规模调度；CARLOS[8]等人对瓶颈等级进行了划分以实现瓶颈漂移的预测；MILTON[9]等采用数学分析方法和仿真技术对瓶颈预测问题进行了研究。花季伟等[10]设计遗传算法并且建立了批决策和批调度的计划调度模型。

3 调度问题概述

半导体行业一直都面临着最具挑战性快速发展问题。本文主要基于工作和资源动态优化匹配半导体生产调度研究。半导体生产主要包括以下两个阶段：晶圆生产(前端)，封装测试(也被称为后端，后端)。其中，封装测试(Assembly and Test Manufacturing，ATM)是中国半导体行业的第一次转型，也是最适合中国行业发展的，也是目前中国半导体行业关注的焦点。

目前，国内大部分封测企业都实施了ERP、MES和EAP系统，这些系统可以提供透明管理的生产和提高生产效率。对半导体生产调度的研究已成为企业面临的常见问题之一。

制造过程中存在各种异常情况，包括设备故障，处理时间不确定性，返工和紧急任务插入。生产调度应该允许计划调整以适应生产中发生的异常情况。需要使用批次拆分调度策略来处理混合生产模式的计划。批量调度策略是将整个任务分为半任务批量和全批量任务。然后根据传感器的不同，会有两批分批到半批次和整批任务，过程如图1所示。

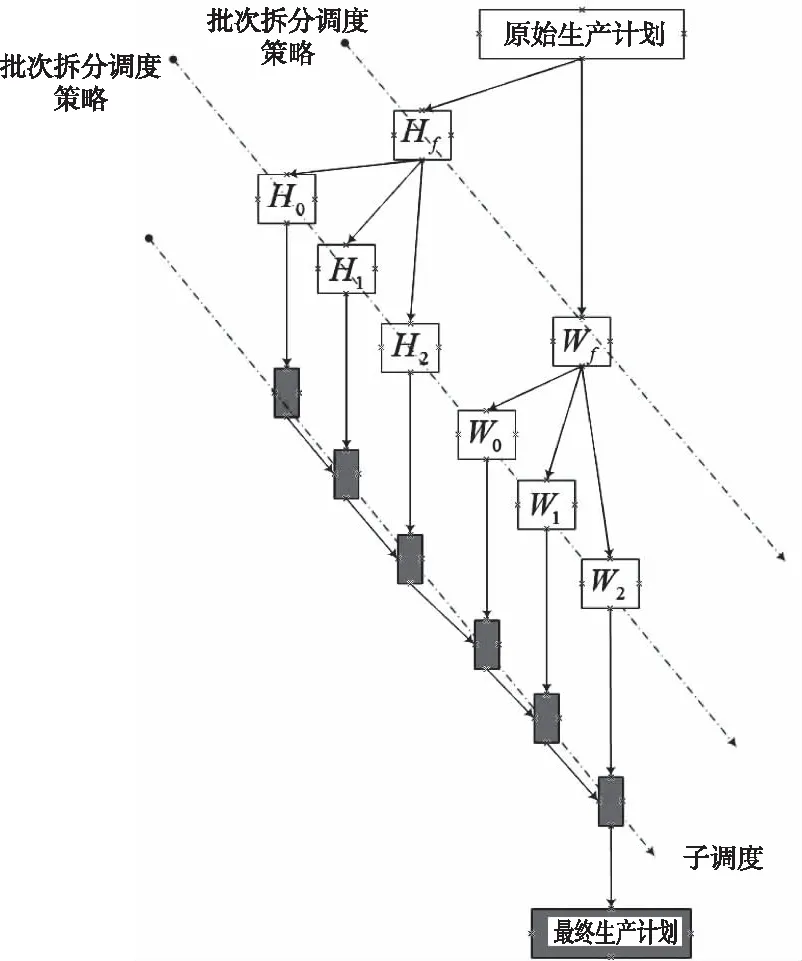
图1 生产计划分解流程

Hf是半批次计划，Wf是全批次计划，Hf⊂Ω∪Ω*，Wf⊂Ω∪Ω*。

其步骤可总结如下：

1)根据当前时间Tnow设置Hf，Wf；

2)根据任务，截止期传感器和无截止期传感器，把半批次进行二次分批，设置Hf为H0、H1和H2；

3)全批次任务也分批为H0，H1和H2；

4)把现有的任务截止期汇聚的时候要增加新的限制条件，有截止期的要有开始时间限制，没有截止期的没有限制。

4 构建数学模型

设置参数如表1所示。

表1 参数设置

建立半导体混合计划和调度的数学模型约束如下

(1)

XSI(i，j)，j′，k-Xijk≥ptijk，i∈Ω，SI(i，j，k)∈Ω

j=1，…，mi，j′∈ΘSI(i，j，k)

(2)

j=1，…，mi-1，j+1∈Θi

(3)

XSI(i，mi，k)，mSI(i，mi，k)-Xi，mi，k≥ptijk+adjtcast

i∈Ω，SI(i，j，k)∈Ω0，mSI(i，mi，k)∈ΘSI(i，mi，k)

(4)

Xi，j，k≥0，i∈Ω，j∈Θi

(5)

(6)

当最后一个设备结束时，相同的设备只能处理下一个任务。约束(2)表示处理时间的限制。约束(3)代表了工作秩序的约束。当最后一个结束时，相同的任务只能继续下一个工位。约束(4)表示相邻任务之间存在建立时间间隔。约束(5)表示决策变量是非负的。约束条件(6)表示有截止期的任务必须在截止期之前完成生产。

5 解决方案

5.1 基于时间和路径的全任务混合计划的解决方案

通过考虑最优设备和工位，选择加工设备和开始时间。最优设备的选择规则如下：

选择最早开始生产工位的规则是

R1=min{sti，mi，kyi，mi，k}

(7)

根据规则R1选择任务i的操作工位，当有多个工位时，选择工位加工时间最短的工位，如下所示

(8)

具有截止期的生产应该提前进行

(9)

无截止期的生产计划的设备选择规则如下所示

T1={pti′jk≥∑(etijk-stSI(i，j，k)，j，k)}

(10)

在开始生产时选择设备T1，选择完T1后，确定任务的开始时间，规则如下

(11)

然后继续使用T1选择设备，确定任务在工位上的开始时间。

5.2 基于锁定路径的半批次混合计划的解决办法

建立混合计划的优先约束：

1)若δ(i，j，k)→(i′，j，k)≥0，i∈Ω且δ(i′，j，k)→(i，j，k)<0，则任务i比任务i′具有更高优先级；

2)若δ(i′，j，k)→(i，j，k)≥0，i∈Ω且δ(i，j，k)→(i′，j，k)<0，则任务i′比任务i具有更高优先级；

3)若δ(i，j，k)→(i′，j，k)<0，i∈Ω且δ(i′，j，k)→(i，j，k)<0则没有优先级约束满足调度；

4)若δ(i，j，k)→(i′，j，k)≥0，i∈Ω且δ(i′，j，k)→(i，j，k)≥0，则它们有相同优先级；

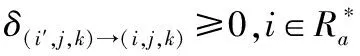
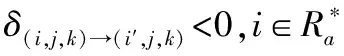
当它们具有相同的优先级时，这两项任务的选择是基于调度顺序的灵活性，调度顺序的灵活性评估方法如下：

φ((i，j，k)(i′，j，k))

(12)

解决方案步骤如下：

1)获得半任务集合H1，有截止期计划集合H0和无截止期计划集合H2，然后根据设备启动时间得到降序排列图；

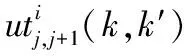
3)计算δ(i，j，k)→(i′，j，k)和δ(i′，j，k)→(i，j，k)；

4)若其中一个排序决策满足规则1至4，则获得半任务集H1。从H1中选择最早任务的开始时间，获得下一阶段的开始时间。计算δ(i，j，k)→(i′，j，k)和δ(i′，j，k)→(i，j，k)。若其中一个排序决策符合规则1或4，则根据约束在此阶段符合任务的处理开始时间。然后跳到步骤5)；若符合规则1，则回顾一下；若没有顺序决定符合规则1，2或3，则跳转到步骤7)；

5)添加新任务并跳到步骤 4)；

6)每个之前没有分类边界的任务要计算φ((i，j，k)(i′，j，k))。选择最小的任务并安排时间。若δ(i，j，k)→(i′，j，k)≥δ(i′，j，k)→(i，j，k)，则任务i要优于任务i′在工位j的设备k上生产，否则在任务i′之后生产，跳到步骤5)；

7)若没有排序决策满足规则4，则寻求解决方案以获得任务的半任务计划，然后停止。否则跳转到步骤6)；若符合规则5或6，则按照约束在该阶段确定任务的处理开始时间，然后跳转到步骤8)；若符合规则7，则回顾一下；若没有顺序决定符合规则1到8，则跳到步骤10)；

8)添加新任务并跳到步骤1)；

9)每个之前没有分类边界的任务要计算φ((i，j，k)(i′，j，k))。选择最小的任务并安排时间。若δ(i，j，k)→(i′，j，k)≥δ(i′，j，k)→(i，j，k)，则任务i要优于任务i′在工位j的设备k上生产，否则在任务i′之后生产，跳到步骤8)；

10)若没有排序决策满足规则8，则寻求解决方案以获得传感器的半任务计划，然后停止。否则，跳转到步骤9)。

6 仿真运算结果

在现实世界中，影响测试结果的因素不止一个，不同因素对测试结果也有不同影响，当影响因素数量和水平提高时，如果综合测试，测试次数会是测试急剧增加安排所有测试非常困难。如何科学地设计测试以获得高可靠性测试数据是研究人员和工程师在实验设计中需要解决的最大问题。

正交表是利用数学原理来生成一个很好的标准化表格。正交设计是使用正交表设计测试，这种设计方法被称为正交优化。在数学中，两个向量的内积之和为零，即a1b1+a2b2…anbn=0，则说这两个向量是正交的。对于4因素和3等级测试，只需要9个测试，这9个测试通常是线性空间的一些正交点。由于正交表构造了均衡(均匀分散)的优势，它可以用它来选择一些具有强表示的实验来获得最佳或更好的值。

6.1 正交设计的特点和步骤

正交设计具有均匀分散，齐整可比的特点。

1)均匀分散

正交表中任何一列的数量级别相等(不同的数字代表不同的级别)。两列之间各种级别的所有可能组合出现并等于出现次数。每个因素的一个等级等于另一个等级的其它等级的可能组合的数量，表明任何两列之间的匹配是一致的。所谓均匀分散，是指利用正交表所选的组合水平的组合，各级的分配均匀。

2)齐整可比

巧妙的可比性意味着每个因素的每个等级都是可比的。因为在正交表中的每个因素的任何水平上，其它因素的所有水平都是平衡的。

3)代表

正交表中任何列的级别都会显示，以便所有测试都包括所有因素的所有级别；任何两列的所有水平组合都出现，允许任何两个因素的组合成为一个全面的测试。由于正交表的平衡色散，可以看出正交设计点均匀分布在综合测试点上，具有很好的代表性。因此，一些试验的最佳条件应与综合试验的最佳条件一致。

正交设计的主要步骤如下：

1)根据目标和测试需求确定等级；

2)选择合适的正交表并确定测试程序；

3)组织实施测试；

4)测试结果分析。

6.2 正确的因素和表格选择

因素水平的选择主要是根据研究目标来确定的，因此首先分析哪些因素会影响目标，并根据实验成本和正交表确定最终因子。水平值的选择基于实验的经验值来确定或随机给定。

正交设计是选择合适正交表的关键，正交表选择直接影响实验结果和实验结果的分析。通常选择正交表要经过三个步骤：一是根据研究内容确定研究因素和水平；其次，根据测试条件，确定试验次数；三，上述情况选择正交表L。

正交表符号的解释

正交表的一般形式是Lt(nq)，符号如下：

L代表正交表；

T=正交表的行数也是试验次数；

N=因素的数量；

Q=正交表的列数以容纳最大数量的因子；

T=nq，q=因数=基本列数。

1)组织实施测试

将事先确定的实验因素，列数的级别按照正交表的数量来安排因素和数值的高低，以便执行该表，根据实验的实验次数为了试验n次。

2)作为趋势图

在本文中，选择最小的正交表L4(23)来说明如何使用正交试验结果作为趋势图。首先，将相同水平的相应实验结果相同的因子相加，得到Ⅰ和Ⅱ的相应值，然后求出I/kj和Ⅱ/kj的平均值。最后，利用水平轴的因子和水平值，以及其相应的垂直轴平均值可以得出相应的趋势。

表2 正交试验结果表

为了进一步研究启发式方法的效果，分析了参数变化的影响。如图2所示，随着调度规模的增加，算法性能不断下降。同时，若有更多性能更好的设备和更多的设备，则算法的性能会不断提高。

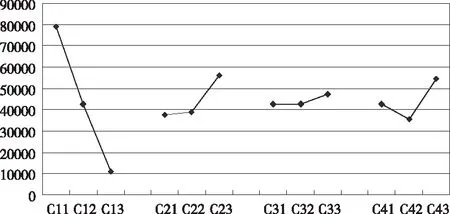
图2 趋势图

对改进的调度算法和模型系统进行了比较。每个方案的完成时间如图3所示有35个方案。使用改进算法，平均任务完成时间缩短12.1分钟。改进的算法具有更好的性能。

图3 时间比较

在工厂应用操作后，性能指标如下：平均规划时间为9.1秒；动态调整时间约为5.2秒。

7 结论

本文针对半导体生产调度优化问题，在调度之前匹配作业和资源，降低了半导体生产调度问题的复杂性，体现了该方法的创新点和可行性。在本文中，根据实际产品流程的流程，描述调度过程。并在分析过程复杂性的基础上，建立数学模型，提出传感器调度算法解决难题。利用实际数据对算法进行测试，验证改进的调度算法是有效的。文中的半导体生产时间表分析是在大型企业的工厂背景下进行的，具有一定的工程应用基础。