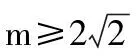陶瓷复合结构抗侵彻行为的近场动力学研究

吴远丽，刘立胜，赖 欣，刘齐文

(武汉理工大学新材料力学理论与应用湖北省重点实验室，湖北 武汉 430070)

1 引言

陶瓷/金属复合结构是陶瓷复合装甲的典型结构。该结构在受到冲击后的力学行为一般可分为8个阶段：初始开坑阶段、陶瓷裂纹扩展阶段、陶瓷锥形成阶段、陶瓷锥运动消蚀阶段、弹体冲击金属背板阶段、定常侵彻阶段、贯穿阶段和完全贯穿阶段。Wilkins[1]和江怡[2]的研究指出在复合结构中，陶瓷面板会在与弹丸接触处产生陶瓷锥，陶瓷锥在弹丸作用下向前运动，使得金属背板受力范围增大，减小了弹丸对背板的冲击作用，金属背板则起到了支撑陶瓷面板，避免了陶瓷板过早的破碎与飞溅，能更充分地耗散弹丸的动能，从而起到有效的防护作用。由于陶瓷复合装甲服役中面临的都是高速冲击载荷，在这些载荷的作用结构的损伤和破坏过程难以观察，在过去的很长一段时间里，陶瓷复合装甲的设计常采用实验和经验的方法来进行设计。在上世纪90年代后，随着计算机的高速发展，高速侵彻问题数值模拟理论和技术逐渐涌现出来，并被用于复合装甲的设计中，取得了很好的效果[2-4]。

相比于实验，数值模拟技术可以有效再现侵彻的全过程，从而能够更深入研究陶瓷/金属复合靶板受到高速冲击载荷过程的破坏机理。该方法操作简便，避免了过多的简化，结果简单直观，能定性定量的分析所需的结果，因此数值分析方法已成为研究复合装甲侵彻问题的主要手段。目前用于侵彻仿真的数值模拟方法主要有：有限元法(FEM)、光滑粒子流体动力学方法(SPH)与近场动力学方法(PD)。有限元法可有效的计算出侵彻过程中靶板吸收的能量等信息，Goh[5]利用有限元法对复合靶板的侵彻与破坏过程进行仿真，得到通过提高背板硬度进而可以改善靶板性能的结论。但是，目前有限元算法为了解决在侵彻过程中因弹体与靶板大变形引起的网格畸变问题[5]，引入了侵蚀算法删除畸变单元，但是这种操作会给体系的质量、能量和精度带来损失，这些都会导致结果失真[6]。光滑粒子流体动力学方法(SPH)与近场动力学方法(PD)都属于无网格方法，这就避免了网格畸变问题。SPH方法利用核积分将一组离散粒子近似合并成一个连续场，然而这种处理方式可能会导致结果出现不稳定性和不一致性[7]，而使用近场动力学理论可有效的避免这个问题。

Silling[8]于2000年提出了近场动力学理论，该理论通过考虑材料点的相互作用来描述材料的力学行为。近场动力学方法是一个以非局域积分公式为基础的无网格法，其空间的离散化是通过材料的粒子(或点)而达到的。由于其无网格的性质以及非局域的性质，近场动力学尤其适合模拟材料损伤，断裂和碎裂。Ning Liu[9]采用基于键的近场动力学方法研究了带有偏心缺口的梁的冲击损伤，广泛用于研究脆性材料中I-II混合裂纹的扩展，证明了使用近场动力学研究脆性材料侵彻问题的有效性。Henke与Shanbhag[10]讨论了基于态的近场动力学理论的网格敏感性对于单层板冲击过程的影响，认为近场作用范围为4倍粒子间距时结果较为稳定。近场动力学方法的计算具有强烈的网格依赖性，当影响函数与近场作用范围共同作用时对于结果的影响很大，故而讨论近场动力学理论对于复合靶板冲击过程的适用性问题非常有研究价值。

分析以上国内外研究现状可知，目前使用近场动力学方法计算冲击问题的研究较少，特别是复合靶板的侵彻问题。本文利用基于态的近场动力学方法对弹体侵彻陶瓷/金属复合结构问题进行计算，证明了其计算高速冲击问题的有效性。讨论了近场作用范围及影响函数对于结果的影响，给出了计算高速冲击复合靶板得到可信结果的最小近场作用范围，及其适用的影响函数。

2 近场动力学的态理论

2.1 常规态理论

基于态的近场动力学理论较传统的近场动力学理论有更多的本构模型，不同于键理论只适用于脆性材料，态理论可以同时计算脆性、弹塑性、粘塑性等多种材料，故而适用于模拟复合靶板的冲击问题。

态理论是用一个非局域的微分积分方法，通过考察组成物质体的材料点间的相互作用而描述某一连续体的动力学行为[11]。确定某一物质体Β∈R3，材料点x位于该物质体Β内，近场作用范围为以δ为半径的球体Hx，则材料点在该近场作用范围中与其它材料点相互作用，如图1。则有参考位置矢量态

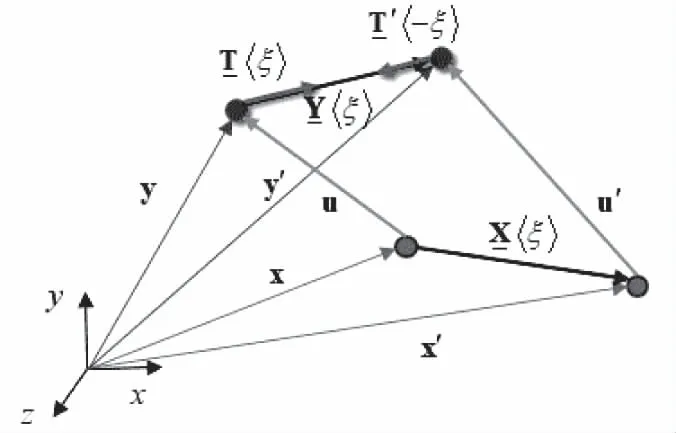
图1 粒子间相互作用

(1)

其中x′为x的近场作用范围中的某一点。

经过时间t的运动过后，该材料点的位置矢量为:

y=x+u(x，t)

(2)

其中u为位移矢量。在变形后，当前坐标系下的成键可由变形态矢量表达为

(3)

在基于态的近场动力学理论中，其运动方程为

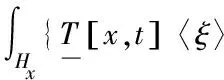
(4)

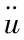
为了满足动量守恒定律，在物质体B中，需满足

(5)

由上式可看出，在近场动力学理论中，没有求导项，也不要求位移一定连续，故而应用于基本方程求解时，解决了有限单元法不适用于求解裂纹等问题的缺陷。

近场动力学中标量扩展态与加权体积的计算结合了本构模型与标量扩展状态e。态理论中的本构方程与其息息相关。

标量扩展态为

(6)

加权体积为

(7)

膨胀

(8)

在介绍上述两个方程时引入了一个新的态ω，表示影响函数，H为近场作用范围。可看出，影响函数与近场作用范围对于计算过程中各值的影响较大。此时加权体积和膨胀的定义引入了两种状态之间的点积。点积中的每一个态都是在一个点上定义的，与点积相关的积分是在这个点的邻域上。因此点积会产生一个依赖于点的量(在这两种情况下是标量)。

偏扩展态为

(9)

普通材料的矢量力状态定义为

(10)

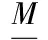
2.2 本构模型

本文计算的靶板材料为氧化铝陶瓷与高强度钢，对应的本构分别为弹性本构与弹塑性本构。

2.2.1 弹性本构

在近场动力学理论中弹性材料在能量平衡方面有与经典理论中弹性材料相似的性质，陶瓷是典型的弹脆性材料，故而使用该本构能很好地模拟陶瓷在侵彻过程中的破坏问题。

若存在可微标量函数W(·)：Β→R3，有

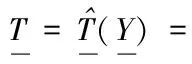
(11)

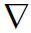
(12)

式(12)分别代表总动能，总对外做功及总应变能。并有

U(t)=K(t)+Φ(t)

(13)

对于弹性材料，标量力态可表示为

(14)

其中k是体积模量，α是剪切模量的标量倍，ω是影响方程。虽然上述关系分别与θ和ed呈线性关系，但仍与位移呈非线性关系。

2.2.2 弹塑性模型

对于弹塑性模型，该近场动力学模型遵循与率无关的J2塑性理论。适用于模拟金属在受到冲击后产生的大变形问题。在局部塑性理论(LTP)中，状态变量是必需的，而在近场动力学中，该值是一个标量的偏塑性变形状态。由于LTP与近场动力学的弹塑性本构模型有密切的相似性，许多用于积分LTP速率方程的逻辑被引入本构模型。

近场动力学塑性本构模型的一个关键组成部分是将标量扩展状态分解为膨胀和偏曲部分，以及将偏曲状态加性分解为弹性ede和塑性edp部分。虽然偏差扩展状态的本质与局部理论有本质上的不同，但从概念上讲，这两种分解都用于LTP。将式(9)中给出的总偏差扩展状态加和分解为弹塑性两部分

ed=ede+edp

(15)

由于观察到许多延性材料塑性变形与压力无关，将式(14)中给出的各向同性弹性本构模型用加法分解为

(16)

其中p=-kθ为近场动力学压力，k是体积模量。上述方程的率形式为：

(17)

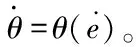
2.3 影响函数

本文主要采取三种影响函数以研究其对于结果的影响，分别为“一”型影响函数函数、抛物线衰变影响函数与高斯影响函数。

1)“一”型影响函数为最基础的影响函数，其表达式为

(18)

2)抛物线衰变影响函数为

(19)

3)高斯影响函数为

(20)

2.4 损伤模型

近场动力学理论考虑两材料点的相互作用，当材料点x′处于材料点x的近场作用范围中时其相互作用。经过时间t后；两材料点经过一定的相对位移，点对的伸长率为s，当s大于临界伸长率sc时，两材料点不再相互作用。使用μ(ξ，t)来表征材料点对的破坏情况，即

(21)

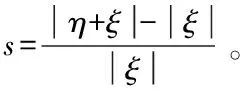
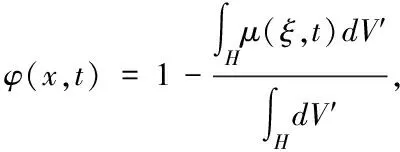
对于态理论中的三维问题[11]，临界伸长率可表示为

(22)

其中G0c为材料的断裂能，G为材料的剪切模量。

2.5 计算模型与参数选取

模型由三种不同材料组成，弹头直径为7.62mm，总重量9.6g，速度v=850m/s。陶瓷板材料为氧化铝，尺寸为50mm*50mm*5mm，金属背板使用的是4340钢，长宽与陶瓷板尺寸相同，高H=8mm。

2.5.1 近场动力学理论计算参数选取

氧化铝陶瓷使用弹性本构模型，4340钢使用弹塑性本构模型。由于重点在于观察靶板破坏情况，故而仅将损伤模型用于陶瓷面板与金属背板，即仅陶瓷面板与金属背板具有断裂极限。

现建立模型，由弹头、陶瓷板与金属背板组成，如表1。

表1 PD理论的计算参数

模型粒子间距Δx=0.00025m，近场作用范围δ=3.16Δx。其中密度与运动方程有关，弹性模量与泊松比是计算力态所用的一部分，计算临界伸长率的断裂能由断裂韧性等得出，见下式

(23)

2.5.2 有限元计算参数选取

氧化铝陶瓷材料选用JH-2模型，JH-2模型是可以模拟损伤的一种材料模型，如图1损伤通过一个损伤量D来控制，D的范围为0-1：当D=0时，材料内无损伤，即为完整材料，当D=1时，即材料完全破坏。如图1所示。4340金属背板使用的是JC模型，该模型能够很好地描述金属材料在大变形下的动态力学行为，因此在金属材料冲击爆炸问题的数值分析中得到了广泛应用。

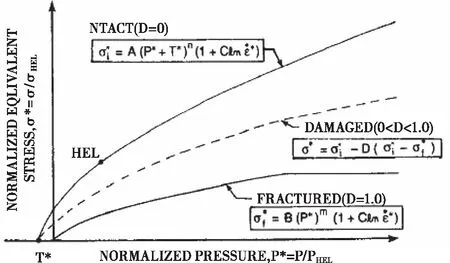
图2 含损伤的强度模型[13]

表2 Al2O3陶瓷材料JH-2模型参数[14]

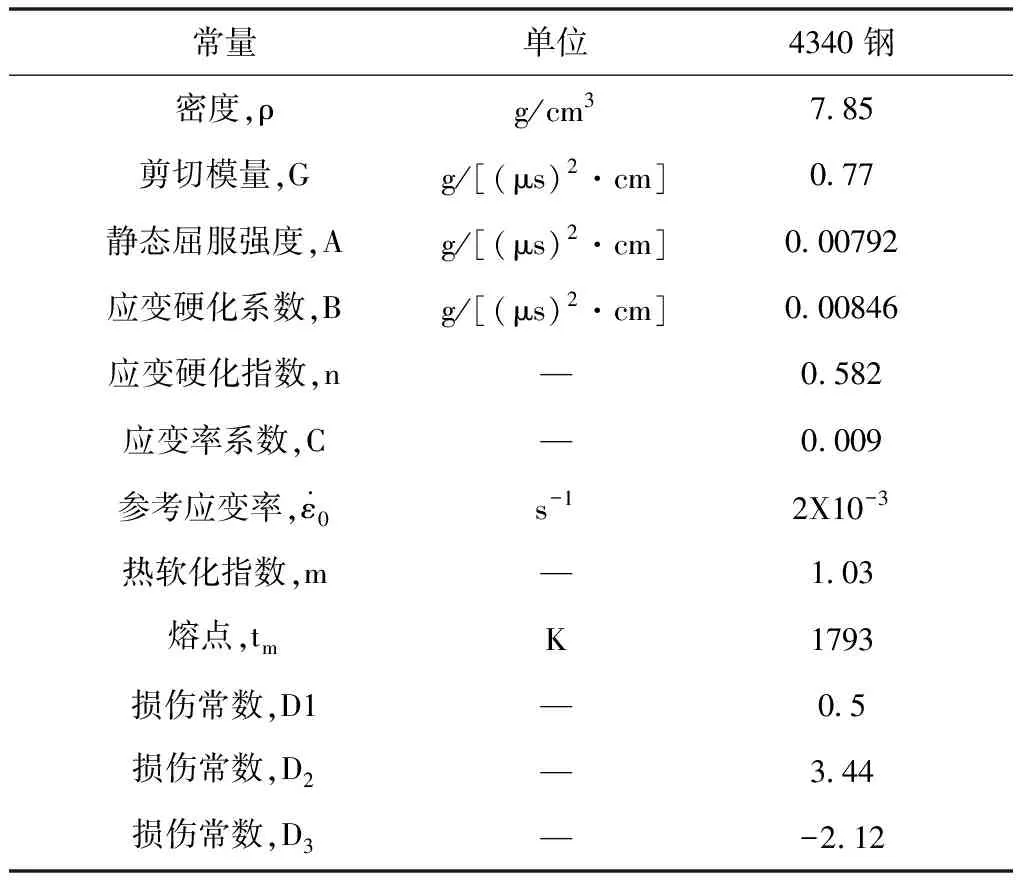
表3 背板4030钢JC模型参数[15]

3 结果与讨论

3.1 对比验证

基于近场动力学态理论，现对于该复合靶板的冲击问题进行对比验证。

在冲击陶瓷复合靶板的过程中，控制损伤演化的失效机制是复杂的，但可以用四种常见的失效模式来描述弹丸对陶瓷的冲击，即晶格塑性、微裂纹、径向裂纹和锥形裂纹。在准静态变形下，当弹头对纯弹性脆性材料施加载荷时，会形成锥形裂纹，称为赫兹锥，圆盘外的径向应力为拉伸应力，圆周应力为压缩应力。当弹头的压缩载荷逐渐增大时，接触圆半径逐渐增大，直到接触圆半径达到一个临界值，该临界值与材料的断裂韧性有关，形成一个临界半径的表面环裂纹。图2为PD、有限元与实验结果的对比，可以看到PD计算的结果比较好的吻合了实验结果，且较于有限元计算的结果更符合理论上的裂纹扩展。

图2 (a)为近场动力学计算结果；(b)为有限元程序计算结果；(c)为实验结果[16]

图3 弹头冲击后的复合靶板剖面图

陶瓷面板的主要破坏形式为陶瓷锥破坏，Woodward[17]通过实验测得当靶板受侵彻速度在220-1000m/s时陶瓷锥角度θ 的变化范围，并给出经验公式

(24)

其中，θ的单位为角度。即可算出速度为850m/s时，陶瓷锥角应为60.1度。使用近场动力学理论计算结果显示陶瓷锥角为57.35度，如图4。图5给出了使用近场动力学计算的剩余速度与使用有限元程序计算的速度变化的对比，可以看到两条速度曲线在下降时均出现拐点，此时弹头穿过陶瓷板接触到金属背板继续向下冲击，使用PD计算的速度较有限元方法计算的速度下降趋势缓略慢，但相差不大，证明了PD计算冲击问题的有效性。

图4 陶瓷锥角

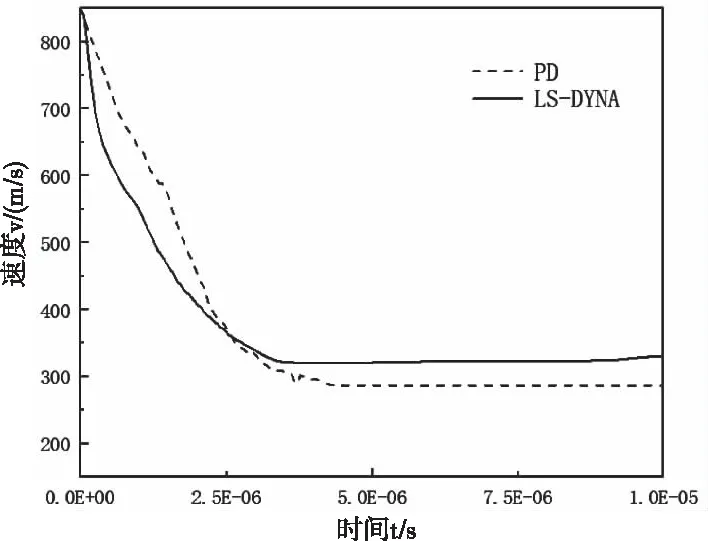
图5 PD与有限元计算弹头的速度变化

3.2 不同近场作用范围与影响函数计算结果对比

表4 陶瓷板正面损伤图

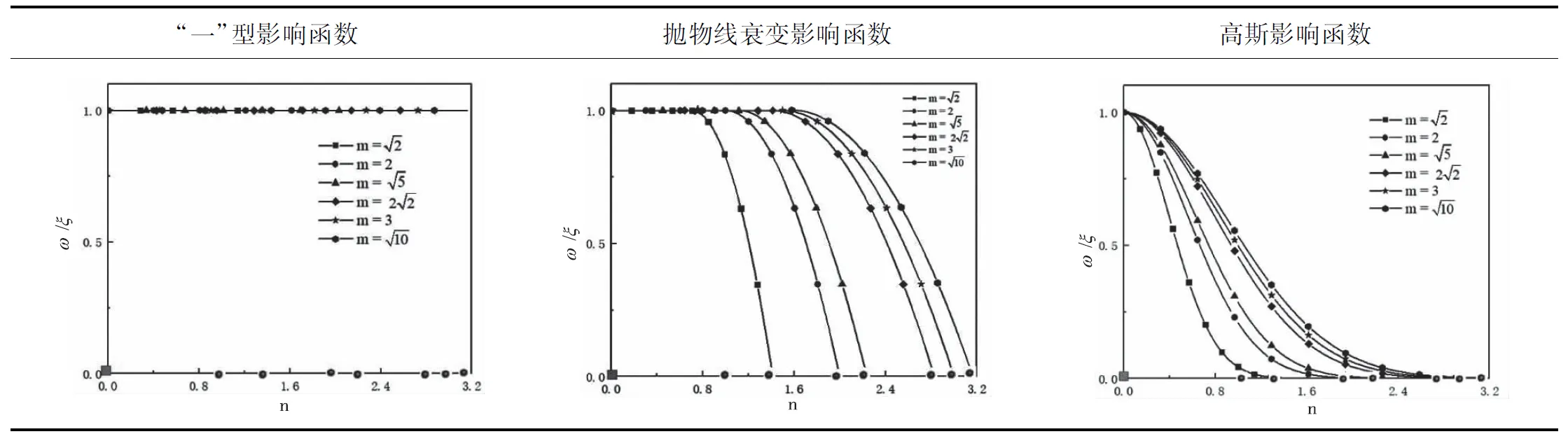
表5 不同近场作用范围下的影响函数

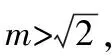
4 结论

本文使用近场动力学方法建立了陶瓷/金属复合靶板受弹体侵彻的离散模型，模拟了陶瓷/金属靶板的侵彻过程，并得出了以下结论：

1)通过模拟获得了弹头在侵彻过程中的速度随时间的变化曲线、靶板的裂纹扩展情况与粒子飞溅模式。并将PD仿真结果与实验及有限元结果进行了对比。对比结果表明，当采用合适的本构描述、影响函数和近场作用范围时，近场动力学方法可以有效、准确地模拟陶瓷/金属复合结构受弹体侵彻的问题。