基于模糊自抗扰的开关磁阻电机转速控制

邓冉冉，栾 茹

(北京建筑大学电气与信息工程学院，北京 100044)

1 引言

开关磁阻电机(switched reluctance motor，SRM)因其具有结构简单、坚固、调速范围宽，动态响应好等特点，使其成为是目前国际上电动车辆驱动系统优选方案之一[1-2]。然而，由于其自身的双凸极结构、开关形式的供电方式、以及铁心磁路的高度饱和等特点，使SRM中的各个物理量存在较强的非线性。其次，由于电动汽车运行时会出现负载转速突变，频繁启停等状况，对系统启动，转速响应，抗干扰能力上具有较高要求，因此近年来国内外学者对SRM 转速控制提出多种策略。文献[3]将CMAD与PID结合对转速实现复合控制。文献[4]将常规滑膜转速调节器与模糊控制相结合的方式，实现转速控制。文献[5]利用单神经元自学习性与PID控制器相结合，同时将模糊控制运用到增益整定上，构建转速控制器。上述控制策略都在一定程度上解决了开关磁阻电机转速控制问题，但存在计算复杂，运算时间长，时效性差，实际应用率低等问题。

自抗扰控制(Auto Disturbance Rejection Control，简称ADRC)相较于传统PI 控制，特点在于其不依赖于精确的数学模型器，能对系统所受的内、外扰动进行实时估计补偿[6-7]。结合SRM特性及电动汽车运行情况，本文选择自抗扰控制方法对开关磁阻电机进行转速控制，同时结合模糊控制理论，提出一种模糊自抗扰转速控制方法[8-17]，在发挥自抗扰控制器已有优点的同时实现部分参数自学习，自整定功能，减少参数调节，提高系统自适应能力。本文在 Matlab/Simulink 仿真软件中搭建SRM系统仿真模型，通过仿真结果表明，与常规PI转速控制器相比，模糊自抗扰转速控制器控制下的转速具有超调量更小，鲁棒性更好，抗干扰能力强，转速误差小等特点。在开关磁阻电机转速控制方面表现出良好的控制效果。

2 开关磁阻电机数学方程

SRM的第m相的电压方程为

(1)

式中Um为m相电压；Rm为m相电阻；im为m相电流。

根据力学基本定律，可得SRM的机械方程为

(2)

式中，J为转动惯量；Tm为m相转矩；TL为电机负载转矩；D为摩擦阻尼系数。

SRM的平均电磁转矩表达式为

(3)

式中，m为SRM的相数；Nr为SRM的转子齿极数；Tx为任一运行点x处的瞬时相转矩；ξ为相电流的中间变量。

3 SRM模糊自抗扰转速控制器设计

3.1 自抗扰控制器

自抗扰控制器由跟踪微分器(tracking differentiator，TD)、扩张状态观测器(extended state observer，ESO)、非线性状态误差反馈(nonlinear states error feedback，NLSEF)三个环节组成[18]，ADRC原理结构如图1所示。

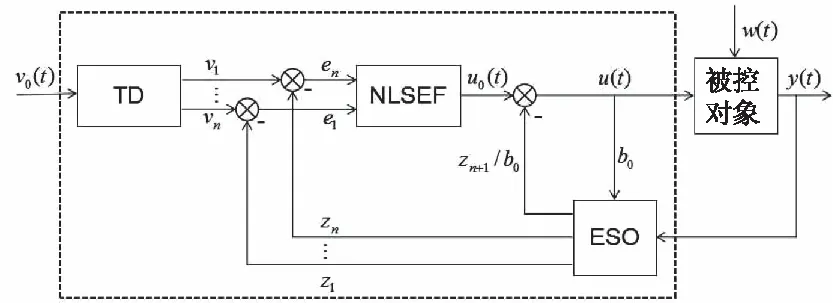
图1 自抗扰控制原理结构图

微分跟踪器(TD)将系统给定信号v0(t)实现过渡过程，以及产生的各阶导数信号。扩张状态观测器(ESO)对被控对象状态变化量进行估计给值z1，同时对系统的总扰动进行观测，给出估计补偿，补偿值为zn+1/b0。非线性状态误差反馈控制律(NLSEF)对送入误差进行计算，得出被控对象的控制量u(t)[9]。

3.2 自抗扰转速控制器设计

对SRM机械方程式(2)进行整理，可以得到

(4)

进一步化简可得

(5)

则SRM转速闭环控制系统可以表示为：

(6)

其中

a(t)包含SRM转速闭环系统的总扰动，包括转速环的定、转子惯量内部扰动与负载突变或摩擦力矩变化等外部扰动。SRM自抗扰转速环结构如图2所示。

图2 一阶自抗扰转速控制原理结构图

其中TD方程为

(7)

ESO方程为

(8)

NLSEF方程为

(9)

非线性函数fal表达式为

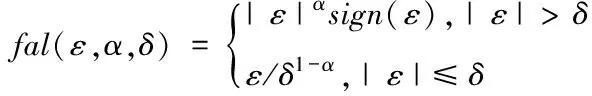
(10)

其中，ω*为给定转速; z11为 ω*的跟踪信号；z21，z22为 ESO 的状态变量，分别为转速反馈和扰动信号的观测值；u0为 NLSEF 处理过的非线性控制量，z22/b 为开关磁阻电机内扰和外扰的补偿值。

3.3 模糊自抗扰(FUZZY-ADRC)转速控制器设计

非线性状态误差反馈控制律(NLSEF)对开关磁阻电机的状态反馈及内外扰动进行实时补偿，是自抗扰控制器的核心部分。而合适的增益值β3可以使自抗扰转速控制器拥有强适应性及鲁棒性。β3值越大，系统响应时间短，速度快，但过大会使系统产生大超调。固定β3值的选定很难满足SRM系统运行中的多种状态。因此，本文利用模糊控制特点，使β3在一定的变化范围内进行修正自整定。同时减少了自抗扰控制器参数在实际操作中的整定难度。FUZZY-ADRC转速控制器结构如图3所示。

图3 模糊自抗扰转速控制结构图

本文利用Matlab中m文件建立模糊控制器，在控制器设计中，以E，EC为模糊变量输入，其中E为跟踪信号z11与扰动信号z21的差值，EC为误差变化率，Δβ3为输出量。

其中E，EC的论域范围为[-1.2，1.2]。Δβ3论域为[-1，1].

隶属度函数均采用对称高斯型属度函数，其中E，EC均分成7个模糊子集，表示成 {PB(正 大)，PM(正 中)，Z(零)，NS(负 小)，NM(负 中)，NB(负 大)}。解模糊化采用平均加权法。根据专家经验建立的模糊规则如表1所示。

表1 Δβ3模糊控制规则表

由上述的模糊规则可以得到一个修正值Δβ3，NLSEF的增益则为β′3=Δβ3+β3，其中基础值Δβ3=20。

4 FUZZY-ADRC-DITC开关磁阻电机转速闭环控制系统

本文开关磁阻电机控制系统采用转速-转矩双闭环控制策略。如图4所示，外环为转速环，通过模糊自抗扰转速控制器得到期望转矩，内环转矩环采用滞环直接瞬时转矩控制方法实现对转矩的实时控制。该双闭环控制，减小SRM 转矩脉动同时对转速实现准确控制，提高系统抗干扰能力。

图4 模糊自抗扰-直接瞬时转矩SRM控制系统

5 仿真结果分析

本文采用MATLAB/SimuLink仿真软件对模糊自抗扰SRM转速闭环控制系统进行仿真，分别对电机起动、给定转速变换、施加负载突增、突然减负载等外在扰动，得到这些情况下的转速波形。同时，对同样的SRM转速闭环控制系统采用PI转速调节器进行仿真比较。

仿真用的电机为三相6/4开关磁阻电机，额定功率为60kW，B=0.02 N·m·s，J=0.005 kg·m2。根据PI试凑调节规律，PI转速控制器参数的设置：比例增益为Kp=50，积分增益为 Ki=10；模糊自抗扰转速控制器参数设置：扩张状态观测器(ESO)中α1=0.95，δ1=0.01，β11=4000，β22=3000，误差反馈控制律(NLSEF)中α2=0.95，δ2=0.01，b2=1500.

5.1 起动情况转速仿真结果

图5图6分别为1000 r/min，空载起动时转速的变化曲线。由仿真波形图可以看出，PI与模糊自抗扰转速控制器，约都在3.5×10-2时，电机达到给定转速。可以看出，模糊自抗扰转速控制器，能实现电机起动快速性的同时保持微小超调量。

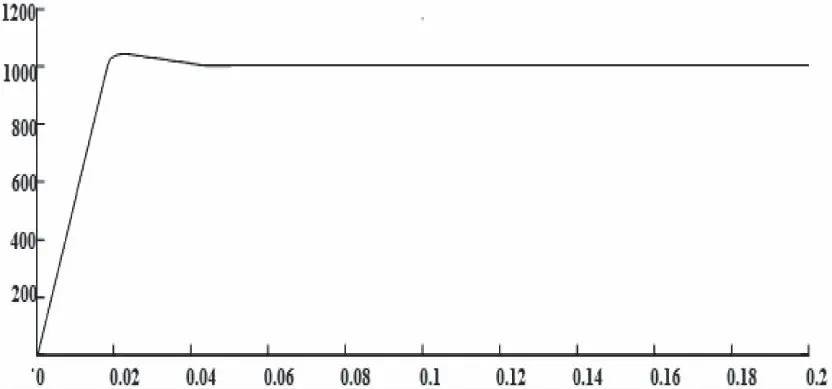
图5 PI控制下空载起动转速仿真波形图

图6 模糊自抗扰控制下空载起动转速仿真波形图

图7图8分别为1000 r/min，负载10 N·m起动时转速变化曲线。由仿真波形图可以看出，PI转速控制器控制时，约0.062s，电机达到给定转速，超调量为2.1%，转速波形波动；在模糊自抗扰转速控制器控制时，约0.054s电机转速达到给定转速，超调量为0.4%。由此可见，在负载起动下，模糊自抗扰控制能实现电机快速起动，且基本实现无超调。

图7 PI控制下负载起动转速仿真波形图

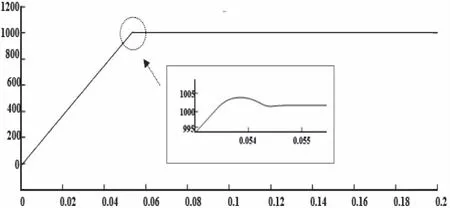
图8 模糊自抗扰控制下负载起动转速仿真波形图

5.2 突加突卸负载情况下转速仿真结果

图9为突加负载时电机在两种转速控制器控制下的转速波形图。其中，给定转速为1000r/min，起始负载转矩为10 N·m，0.1s时负载转矩突加至20 N·m。从仿真结果可以看出，突加负载时系统在模糊自抗扰转速控制器控制下，转速恢复至给定转速时间为2×10-3s，转速突变2 r/min；PI转速控制器控制下，转速恢复至给定转速时间为4×10-3s，转速突变8 r/min.

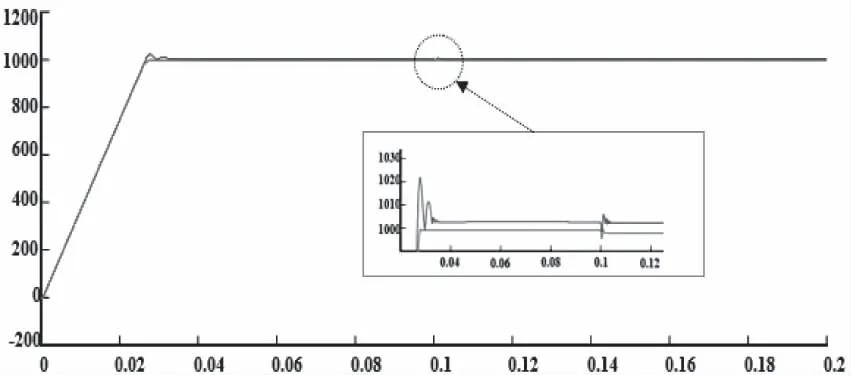
图9 突加负载时转速仿真波形图

图10显示在给定转速不变情况下，负载转矩由起始20 N·m，0.1s时突降至10 N·m时的电机转速仿真结果。模糊自抗扰转速控制器控制下，突卸负载时，转速恢复至给定转速时间同为2×10-3s，转速突变10 r/min；PI转速控制器控制下，转速恢复至给定转速时间为1×10-2s，转速突变21 r/min.

图10 突卸负载时转速仿真波形图

由仿真波形可见，在负载突变情况下，模糊自抗扰控制的转速控制器相较与PI转速控制器，能使转速更快恢复至给定转速，转速波动小，具有良好的抗扰性，满足电动汽车运行时的情况。

5.3 转速跟随性仿真结果

图11及图12为电机转速跟随波形图。以检验在给定转速突变时，模糊自抗扰转速控制器控制转速的跟随性能。图11，负载转矩为10 N·m，起始给定转速为1000 r/min，0.1s时给定转速突增至1200r/min。由仿真波形图看出，PI转速控制器控制下，转速1.14×10-2s稳定达到给定转速，模糊自抗扰控制下6×10-3s转速达到给定值。图12显示在负载转矩为10 N·m时，转速在0.1s从1000 r/min突降至800r/min的仿真情况。从仿真波形图中可以看出，PI转速控制器控制的转速在1×10-2s达到给定，模糊自抗扰转速控制器在5×10-3s内实现稳定，达到给定转速。

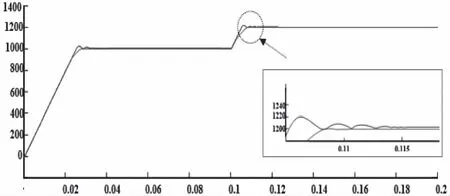
图11 给定转速突增仿真波形图

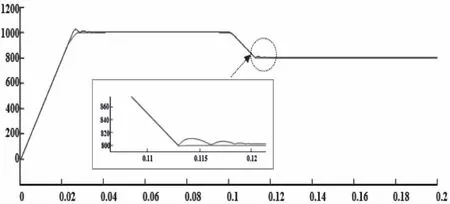
图12 给定转速突降仿真波形图

模糊自抗扰控制转速实现跟随给定快速且能基本实现无超调，转速波动及转速差值小，对系统的整体扰动小。

6 结语

本文采用模糊控制与自抗扰控制相结合的方法构建的模糊自抗扰转速调节器。①实现了自抗扰控制器中NLSEF增益β3的自整定功能;②采用这种模糊自抗扰转速控制器，使SRM调速系统转速波动小，响应速度快、抗干扰能力强、超调量小。提高开关磁阻电机双闭环控制系统的稳定性。经过仿真的比较，其综合控制性能优于传统 PI 转速控制器。