基于SIMD 的并行傅里叶空间图像相似度计算

郭渝洛，边浩东，董润婷，唐嘉豪，王晓英，黄建强

（青海大学 计算机技术与应用系，西宁 810016）

0 概述

二十世纪七十年代，TAYLOR 和GLAESER 研发了冷冻电镜（cryo-Electron Microscopy，cryo-EM）。该项技术发展至今，已经成为研究生物大分子结构与功能强有力的手段，其简化了生物细胞的成像过程，提高了成像质量，将生物化学带入一个新时代［1-3］。

冷冻电镜是在低温下使用透射电子显微镜观察样品的显微技术，即把样品保存在液氮或液氦温度下，通过对其某方向的投影显微像在时空中经调整后进行叠加，从而提高信噪比，最终将不同投影方向的显微像在三维空间进行重构，获得大分子的三维结构。

实际上，基于2D 投影的3D 重构具有挑战性。首先，样品中生物分子在随机分布后具有不同的角度，很难确定它们正确的角度，因此，需要多次迭代步骤才能使最终的模型收敛；其次，为了避免损坏样品，通常使用低剂量的电子束进行辐照，而这样获得的电子显微像具有高噪声和低对比度，需要大量的电子显微图像来生成具有高分辨率的3D 模型。由此可见，冷冻电镜模型重构依赖于数以万计的投影图片进行分析、组装和优化，冷冻电镜三维重构需要超过1 petaflops 的计算能力［4］。

目前许多研究学者对冷冻电镜三维重建计算的优化提出了许多有效的解决方案，如文献［5］基于分块流模型的GPU 集群并行化冷冻电镜三维重建，文献［6］在CPU-GPU 异构系统上并行化冷冻电镜三维重建。

在冷冻电镜三维重构过程中，傅里叶空间图像相似度计算是调用最为频繁的计算，其计算成本较高，存在应用程序尚未充分利用并行化优势、编译器自动对代码进行矢量化的优化效果不佳和数据存储架构导致不必要内存消耗等问题。随着每个芯片处理核数的增加，负载均衡的重要性也在不断提高，处理核的利用率是多核系统性能的一个关键指标［7］。文献［8-9］对经典的负载平衡方法进行了回顾和分类，基于此，本文对程序进行手动负载均衡优化操作，使各处理核对计算任务均衡处理，提高程序的并行效率。

在现代微处理器中，单指令多数据流（Single Instruction Multiple Data，SIMD）作为一种利用通用核中数据级并行性的方法［10］得到了广泛的认可［11］，SIMD 指令集允许程序员与编译器通过CPU 实现数据级并行性，提高运算效率。SIMD 矢量化在稀疏矩阵向量乘法上有着优异的性能提升效果［12］。因此，本文借鉴SpMV 中用SIMD 矢量化对傅里叶空间图像相似度计算进行优化。

随着CPU 计算速度越来越快，处理器速度与访问主内存速度差距日益增大，以至于程序将大部分CPU时间花费在等待内存访问上。缓存（cache）［13］技术能够有效减少磁盘访问次数，提高数据访问效率。但硬件缓存大多依赖于空间局部性来实现高效的内存访问，且多数内存布局优化算法都是基于深入理解程序的算法以及对原有数据结构进行调整。文献［14］指出算法的内存访问模式已成为决定算法运行时间的关键因素，文献［15］则对大网格数据布局进行优化，提高了缓存的一致性，减少了缓存未命中率。

更改数据存储结构能够获得更优的存储分配效果［16］，但原程序中的数据结构在地址空间中分散，不利于内存访问，因此，需要设计新的数据结构实现对空间局部性的有效利用。本文提出一种基于SIMD的并行傅里叶空间图像相似度算法。手动对任务进行均匀分配操作，从而在多核处理器上实现负载均衡，同时使用AVX-512 指令集进行高效的矢量化操作。此外，通过优化原程序中的数据结构并使其字节对齐，降低缓存缺失率。

1 研究背景

1.1 冷冻电镜三维重建

冷冻电镜结构解析的理论基础是电镜三维重构原理［17］，该原理基于数学中的中央截面定理和傅立叶变换的性质。中央截面定理的含义是：一个函数沿某方向投影函数的傅立叶变换等于此函数的傅立叶变换通过原点且垂直于此投影方向的截面函数，即一个生物样品的电镜图像的傅里叶变换等于该三维物体的傅里叶变换通过样品中心（设定为坐标原点）并垂直于摄像方向的截面，如图1 所示。

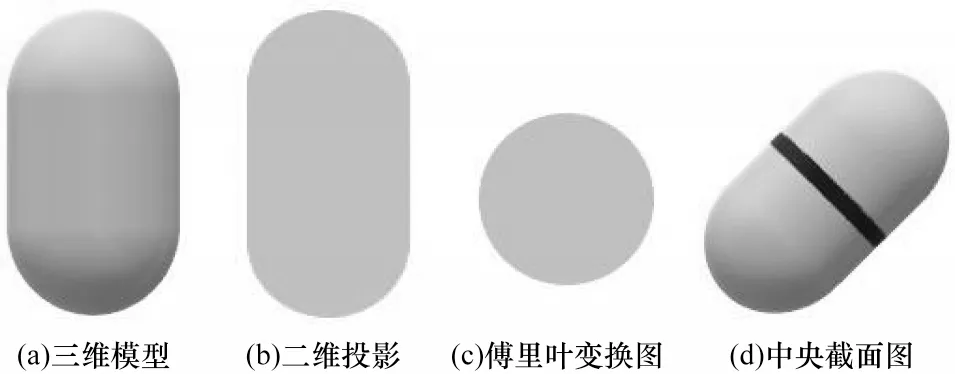
图1 中央截面定理示意图Fig.1 Schematic diagram of central section theorem

由于一个函数的傅立叶变换的逆傅立叶变换等价于原来的函数，因此利用傅里叶变换可以很容易地实现图像的旋转缩放和平移不变性。根据中央截面定理和傅里叶变换的性质，当利用透射电子显微镜获得的生物样品多角度放大电子显微图像足够多时，就能得到生物样品在傅里叶空间的三维信息，再经过傅里叶逆变换便能得到物体的三维结构，如图2 所示［18］。

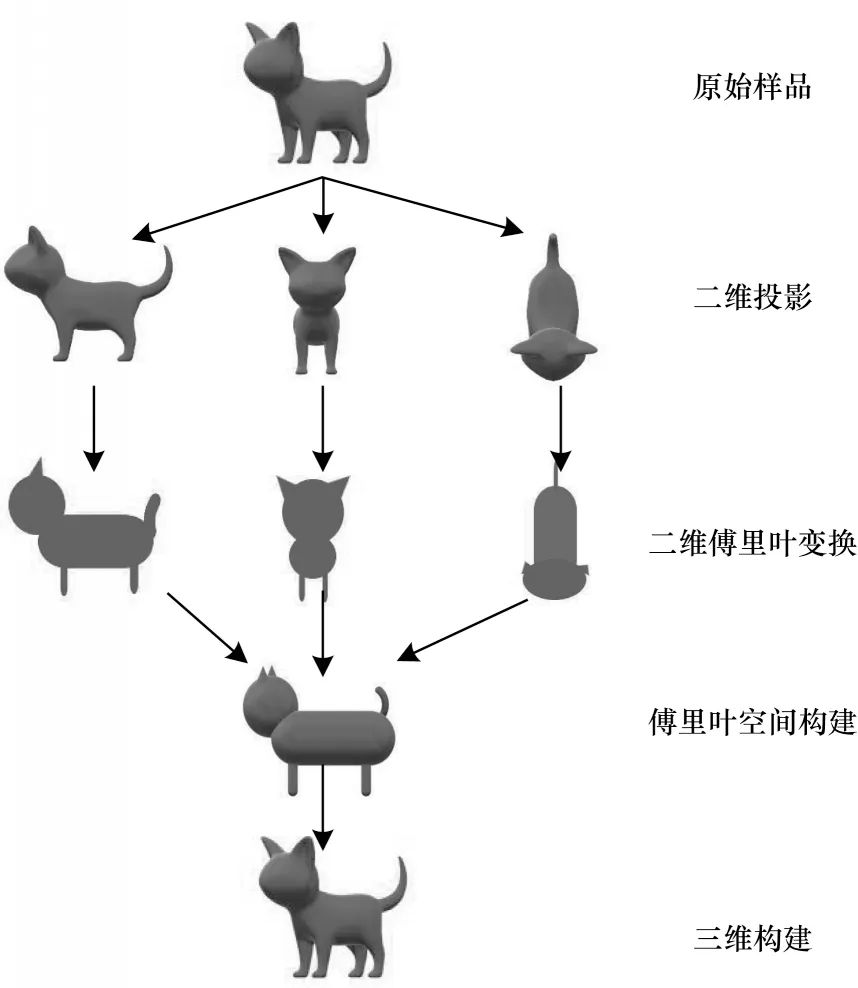
图2 冷冻电镜三维重构过程Fig.2 Three dimensional reconstruction process of cryo-EM

在冷冻电镜结构解析的实践中，可以根据生物样品的性质及其特点，选择不同的显微镜成像及三维重构方法，目前主要使用单颗粒重构、电子断层扫描重构等方法针对不同的生物大分子复合体及亚细胞结构进行解析［19］。

冷冻电镜单粒子法是获得三维重构图像的重要办法［20-21］。单粒子法就是对分离纯化的颗粒分子分别成像，其适合的样品分子量范围为80～50 MD，最高分辨率约3 Å，其基本原理就是基于分子结构同一性的假设，利用不同投影角度的多个分子的显微放大二维图像进行同一分析，通过对正、加和平均等图像操作提高信噪比，最后将不同投影方向的单颗粒显微像在三维空间进行重构，获得三维模型。

1.2 傅里叶空间图像相似度算法

在冷冻电镜数据分析处理中，傅里叶空间图像相似度计算被频繁调用，其主要使用计算样品的二维真实图像与空间中三维重构模型的投影图像之间的相似度，计算公式如下：

傅里叶空间图像相似度计算在程序中的实现代码如算法1 所示，主要计算步骤如图3 所示。

图3 傅里叶空间图像相似度计算的主要步骤Fig.3 Main steps of Fourier space image similarity calculation

首先将disturb0 与ctf 相乘，然后与复数pri 相乘，接着计算dat 与步骤2 结果相减后的范数，与上一步的result 相加后，i加1，重复执行步骤1，直至i=n-1。

算法1串行傅里叶空间图像相似度算法

2 傅里叶空间图像相似度计算优化方法

2.1 手动负载均衡

经过OpenMP 对程序进行并行化处理后，程序具有良好的并行性。但是通过vtune 工具进行分析后，有大量资源花费在了Spin time 上。Spin time 是CPU 繁忙的等待时间，是等待其他同步资源处理的自旋等待时间。当同步API 导致CPU 在软件线程等待进行轮询时，通常会发生这种情况。对于并行程序，并行循环占大部分执行时间。因此，减少并行循环的耗费也是提升整个程序性能的关键，需要对其进行手动负载均衡优化。

首先根据运行环境CPU 的线程数，尽可能将任务均分给每个线程上。如算法2 所示，本文用Begin与end 数组记录下每个线程处理数据的起始点与终点。在函数logDataVSPrior 中将任务均匀地分给每个线程，尽可能使程序负载均衡。在并行循环计算完成后，再对每个线程计算的result 进行累加，如算法3 所示。

算法2根据线程数对任务进行分配

算法3手动负载均衡后的傅里叶空间图像相似度算法

2.2 SIMD 矢量化

SIMD 矢量化操作在优化稀疏矩阵向量乘法上表现优异，其采用一个控制器来控制多个处理器，同时对一组数据中的每一个分别执行相同操作，从而实现空间并行性。利用perf 工具分析特定程序后，编译器已经自动矢量化程序中主要的计算，但仍占据了大量的总体开销。为了提高系统整体性能，需要在程序中手动添加SIMD 内联函数对其进行矢量化优化。从算法4 中可以看出，logDataVSPrior 函数中有大量数据执行单个单元的运算，如乘法、加法和减法，适合使用SIMD 向量化对其进行优化。因此，本文将SIMD 矢量化操作添加到logDataVSPrior 函数中。下文选择INTEL 的AVX-512 指令集，并给出详细优化步骤。

算法4更新数据结构后傅里叶空间图像相似度算法的实现

为了方便使用SIMD 指令集，将复数数组拆分为实部数组和虚部数组，分别对复数的实部和虚部进行计算，SIMD 优化步骤如图4 所示。首先利用_mm512_mul_pd 指令实现实数ctf 与实数disturb0 相乘的操作，并使用_mm512_fnmadd_pd 指令分别计算实部与虚部的值；然后利用_mm512_mul_pd 指令和_mm512_fmadd_pd 指令计算算法 4 中的“real*real+comp*comp”，通 过_mm512_fmadd_pd 指令将步骤4 的计算结果与sigRcp 相乘再与mark 进行相加，并把结果存储在mark 中；重复执行上述步骤，直到本线程上的任务处理完毕；最后利用_mm512_add_pd 指令将每个线程上得到的计算结果进行累加，得到二范数之和。

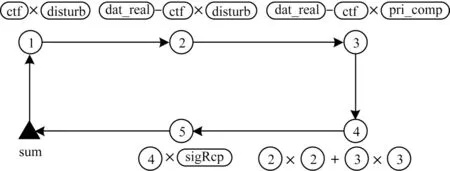
图4 SIMD 优化步骤Fig.4 SIMD optimization step

2.3 内存访问优化

目前CPU 计算速度远超内存访问速度，缓慢的内存访问速度成为限制系统整体性能的主要瓶颈。利用Linux 系统的Perf 工具进行分析，根据分析结果可以推断出，由于较高的LLC 缺失率，CPU 需耗费时间等待从本地或远程DRAM 中获取数据。由于原程序的数据存储架构不利于内存访问，导致不必要的内存消耗，因此提高内存访问效率也是提升整个程序性能的关键。

SIMD 矢量化中提出的数据结构，将复数分为实部向量与虚部向量，在logDataVSPrior 函数计算中存在大量的相对较长数据访问操作，这对内存访问非常不利。如图5 所示，对于需要计算的6 个数组，需要获取6 个位置的数据值，然后进行计算。假设每个数据之间的步长比当前CPU 的缓存行大得多，那么需要执行6 次高速缓存行替换操作才能获得6 个不同位置的值。然而，多次替换高速缓存行的操作会影响缓存性能。

图5 SIMD 优化后的数据结构Fig.5 Data structure after SIMD optimization

为解决这个问题，本文提出一种有效的数据结构。如图6 所示，将6 个不同的数组邻接存放，这样可以将一次循环内需要使用的数据合并到新结构向量中，仅需访问一次索引位置，即可获得需要计算的连续数据。与原来的数据结构相比，合并后的数据结构能够更好地实现缓存数据的重用，提高缓存命中率。这是因为合并后的数据结构使将来用到的数据与当前正在使用的数据在空间地址上相邻，从而减少了替换高速缓存行的操作。

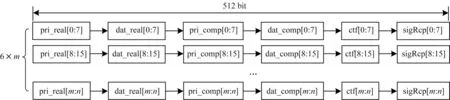
图6 本文提出的数据存储结构Fig.6 Data storage structure proposed in this paper

目前，计算机的内存空间都是按照字节进行划分的，多数CPU 只从对齐的地址开始加载数据，如果数据不按照一定的规则存储，则会降低读取速度，从而影响计算效率。因此，字节对齐在CPU 架构中起着重要的作用。当高速缓存行获取未字节对齐的数据时，会发生图7（a）所示的情况。从图中可以看出，int 类型占用4 Byte 的内存空间，当一个变量int 的起始地址是1 时，那么CPU 需要进行2 次数据读取操作，这是因为仅一次读取操作无法完全获得所需的数据，所以需要多次读取来获取剩余的数据。图7（b）显示了数据按照内存对齐的方式存放后，只需要1 次读取操作就能完全获得所需数据，提高了读取速度。

图7 数据字节对齐操作Fig.7 Data byte alignment operation

3 实验与结果分析

3.1 设备信息

本文使用的实验平台是Intel 的Skylake 架构CPU。对于SIMD 指令集，选择CPU 支持的AVX-512 指令集。快速高效的OpenMP 并行语言用于多线程实现。硬件和软件配置如表1 所示。

表1 实验平台信息Table 1 Experimental platform information

3.2 性能比较与分析

如图8 所示，本文演示了10 000、20 000、40 000、80 000、和100 000 张真实图像与投影图像的所有像素在傅里叶空间中的二范数之和的性能，并比较了4 种不同状态下的加速比性能，即原代码运行时间/优化后代码运行时间。

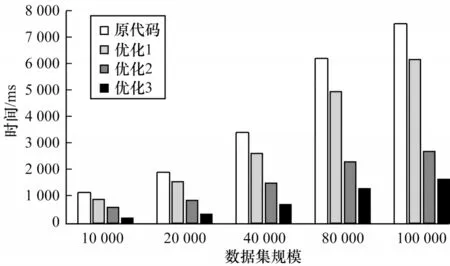
图8 不同大小数据集上的加速比Fig.8 Speedup on different size datasets

在图8 中，原代码表示使用OenMP 进行并行化处理的傅里叶空间图像相似度计算的时间成本，优化1 表示仅实现手动负载均衡优化的时间成本，优化2 表示在优化1 的基础上同时实现手动SIMD 矢量化优化的时间成本，优化3 表示实现第2 节提到的所有优化方法。

在同一实验平台上，可以发现优化1 的时间成本相比原代码有明显的性能提升，主要有以下3 方面原因：

1）在经过手动负载均衡优化后，各处理核对任务均衡处理，进行负载均衡处理的时间成本可以忽略不计，并且能够有效减少负载不均衡导致的回滚次数，提高程序并行效率。

2）实现SIMD 矢量化的优化2 比优化1 具有更快的计算速度，因为自动矢量化并不能充分利用机器中SIMD 的性能，经过手动矢量化后达到了更好的并行效果。

3）优化3 中使用了创新的数据结构以及字节对齐操作，使即将要用到的数据连续存储，实现了优秀的空间局部性，字节对齐操作提高了读取速度。因此，优化3 相较于之前的优化有较明显的性能提升。

对于不同大小的数据集，性能影响会有所不同。从图8 中可以看出，在不同大小的数据集上都有相同的性能优化趋势，在数据集规模为10 000 和20 000 时，程序具有更出色的性能提升效果，这是因为其空间开销接近高速缓存空间大小，较小的内存消耗更适合利用高速缓存的空间局部性。

为更直观地反映本文方法的优化性能，对比不同数据集上的程序加速比性能。如表2 所示。可以看出，与原程序相比，优化后的程序运行时间平均提高了5.132 倍加速比。随着数据集增大，程序性能依旧得到稳定的提高，这表明本文优化方法不会因为数据集增大而导致性能下降。

表2 在不同数据集上的程序加速比Table 2 Program speedup on different datasets

4 结束语

针对傅里叶空间图像相似度算法，本文在单个节点上通过手动负载均衡、手动SIMD 矢量化和内存访问优化这3 种优化方法来获得更高效的性能。测试结果表明，优化后的程序具有更稳定的性能。本文仅对单节点的傅里叶空间图像相似度算法进行优化，下一步将针对多节点上的程序做优化处理和测试。