移动机器人中视觉里程计技术综述

马科伟，张锲石，康宇航，任子良，程 俊

（1.中国科学院深圳先进技术研究院，广东 深圳 518055；2.中国科学院大学 深圳先进技术学院，北京 101408）

0 概述

视觉里程计（Visual Odometry，VO）［1］主要用于移动机器人和智能车辆的自主导航任务，尤其是在未知环境下的目标检测和自身定位中发挥着重要作用。VO 的主要工作原理是在刚体运动过程中，利用摄像头对周围环境采集图像数据，以连续图像序列作为输入信号，通过计算自身的位姿变化以得到运动估计。

早期的里程计技术多为机械式原理，如我国古代的记里鼓车利用齿轮传动机构实现路程计量，而近代出现的电子式里程计则利用电子传感器代替早期的机械部件，从而降低成本、提升可靠性并获取更加准确的里程信息和速度信息。VO 相关研究起 源于20世纪80年代，最早是由MATTHIES 等［2］设计一套包括特征提取、特征匹配、运动估计等模块的理论框架，并一直沿用至今。2004 年，VO 这一概念被DAVID 等［1］正式提出，同年，VO 被NASA 用于火星探测器，自此，VO 被大众熟知并逐渐引起关注。近年来，VO 的相关研究成果已广泛应用于无人驾驶、VR、AR、移动机器人等新兴技术领域。随着人工智能技术的发展，很多基于深度学习的VO方法不断被提出，并在某些性能表现上优于传统方法。

在实际应用中，通常采用实时定位与地图构建（Simultaneous Localization and Mapping，SLAM）［3-4］技术来实现移动机器人的自主建图与导航等需求。SLAM是一种无需外界信号源就能在陌生环境中实现独立自主定位的技术，通过搭载特定的传感器来捕获环境信息，通常包括搭载激光雷达的SLAM 系统和搭载相机的SLAM 系统。其中，搭载相机的SLAM 系统被称为视觉SLAM（Visual SLAM，VSLAM）［5］。VSLAM 注重全局轨迹和地图的一致性，其最终目的是获得一个全局且一致性的机器人运动路径估计，整个系统通常包括传感器数据、前端、后端、回环检测、建图等5个部分。而VO 的研究主要集中在如何根据相邻帧图像定量估算帧间相机的运动，其仅关注局部运动，工作方式是一个位姿接一个位姿地增量式重构地图，且只优化前面若干个路径位姿，因此，VO 通常作为VSLAM 的前端来使用。

为了使得VO 方法可以更好地应用于实际场景，研究人员进行了大量的研究，研究方法主要分为2 类：一类是基于传统几何方法，另一类是基于深度学习方法。本文对VO 方法的发展历程进行概述，分别介绍基于传统几何和基于深度学习的VO 系统，在对VO 进行数学表述的基础上汇总各类方法，并深入探讨直接法和间接法2 类方法。同时归纳目前VO系统研究中常用的公共数据集，并对部分VO 系统进行评价测试，最后对VO 领域的未来发展方向进行展望。

1 传统VO 方法

1.1 VO 的数学表述

VO 系统首先通过传感器采集视觉信息，在获取信息的过程中主要用到透视投影技术，透视投影的原理是将三维世界投影到二维平面，相机模型即基于透视投影，其几何关系如图1 所示。其中：C-xyz为相机坐标系；O-uv为二维投影成像平面；C点为摄像机的光心；C、O之间的距离为相机的焦距。考虑一个空间点P（X，Y，Z）经过投影映射到二维平面的p（u，v）点。

图1 相机几何模型Fig.1 Camera geometry model

从三维空间投影到二维平面的透视投影方程可以表示为：

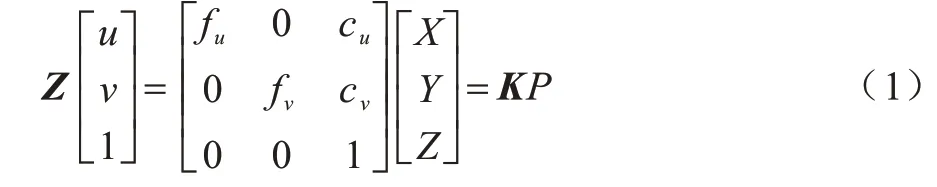
其中：fu、fv是u、v方向上的焦距；cu、cv为二维投影平面的像素从原点处向u、v方向的平移量。fu、fv、cu、cv都属于相机的内部参数，由它们共同组成式（1）中的矩阵，称为相机的内参数矩阵K，相机的内参在出厂后是固定的，不受外界环境影响。

相机在环境中以固定频率采集运动图像，假设在k时刻采集到的图像为Ik，则在一段时间内采集到的图像序列可以表示为I0：n={I0,I1,…,In}，在k-1 时刻至k时刻，相机的坐标变换矩阵T可表示为：

其中：R为旋转矩阵，t为平移向量，它们又称为相机的外参数，均随着相机的运动而发生改变，由它们组成的矩阵T称为变换矩阵（外参数矩阵），其代表着相机轨迹，同时也是VO 中的待估计目标。设相机位姿集C0：n={C0,C1,…,Cn}，通过图像序列可以计算出一系列连续的变换矩阵Tk(k=1,2,…,n)，就可以通过初始位姿C0得到相机的后续运动轨迹Cn=Cn-1×Tn=C0×T1×…×Tn。由于VO 是增量式重建轨迹，因此计算出的轨迹不可避免地会有误差积累，为了减少这种误差，通常使用捆绑调整优化（Bundle Adjustment，BA），通过迭代优化前m帧的重投影误差使得误差累计最小。

1.2 传统VO 方法分类

传统VO 方法是基于模型的系统，按照主流传感器类型可以分为单目（Monocular）、双目（Stereo）、深度相机（RGB-D）三大类，而按照对图像的处理方法可以分为特征点法和直接法两大类。

1.2.1 按传感器类型的分类

只使用一个摄像头的VO 系统称为单目VO 系统，单目相机具有结构简单、成本低的特点，受到众多研究人员的关注，常用的单目VO 系统有PTAM［6］、SVO［7］、DSO［8］等。但是，单目相机在采集数据时往往会丢失一个重要场景维度，即深度。为解决该问题，需要平移单目相机后才能估计深度信息，但通过这一过程仍然无法获得真实距离。

为得到更加准确的深度信息，研究人员尝试使用双目相机和深度相机，这两类相机可以测量物体与相机的距离，从而解决单目相机无法测量距离的缺点。在取得距离之后，场景的三维结构就可以通过图像恢复出来，也消除了尺度的不确定性。双目相机由2 个单目相机组成，常用的双目VO 系统有ORB-SLAM［9］、RTAB-MAP［10］。但是，双目相机的视差计算往往非常消耗资源，这也是双目相机存在的主要问题之一。深度相机主要利用红外结构光或者ToF（Time-of-Flight）原理，通过向目标物体发射光并接收返回的光来测出距离，与双目相机测距原理不同，深度相机是通过物理测量手段获取距离参数，相比于双目相机可节省计算资源，常用的深度VO系统有DVO［11］、RGB-D-SLAM-V2［12］等，但是深度相机存在易受光照影响、无法测量投射材质等不足，且主要用于室内测量，目前难以在室外广泛应用。

1.2.2 按图像处理方法的分类

根据是否直接对图像进行特征提取，传统VO 方法可分为特征点法和直接法两大类。

特征点法首先从图像中选取比较有代表性的点，且这些点在相机视角发生少量改变后依然保持不变，即在各帧图像中尽可能找到相同位置的点，然后基于这些点计算位姿。早期提取的特征以灰度值的形式存在，但灰度值易受光照、形变、材质等影响，在不同图像中变化较大，鲁棒性较差。为了克服这一问题，研究人员设计出更加稳定的图像特征，如SIFT［13］、SURF［14］、ORB［15］等，这些特征相对于早期的特征具有更稳定高效的优势，因此，基于这些特征描述子衍生出了很多算法，如MonoSLAM［16］、PTAM［6］、ORB-SLAM［9］等。杨冬冬等［17］基于SIFT特征提出一种基于局部和全局优化的双目VO，在满足实时性的基础上能够提高精度。但是，通常特征点法中的关键点提取和描述子计算过程都非常耗时，且只使用了图像的少量信息，如遇到某些特征缺失的场景，就难以找到足够多的匹配点来估计相机运动。

特征点法需要消耗大量的资源来计算特征点，直接法则不需要知道点与点之间的对应关系，其只提取关键点，跳过描述子计算，直接根据像素灰度信息来计算相机的运动。常用的基于直接法的VO 系统有DTAM［18］、DSO［8］、DVO［11］等。

由于基于特征点法的VO 系统在SLAM 中更适合回环检测与重定位，因此当前主流的VO 方案更多基于特征点法。常用的基于传统方法的VO 系统性能对比结果如表1 所示。

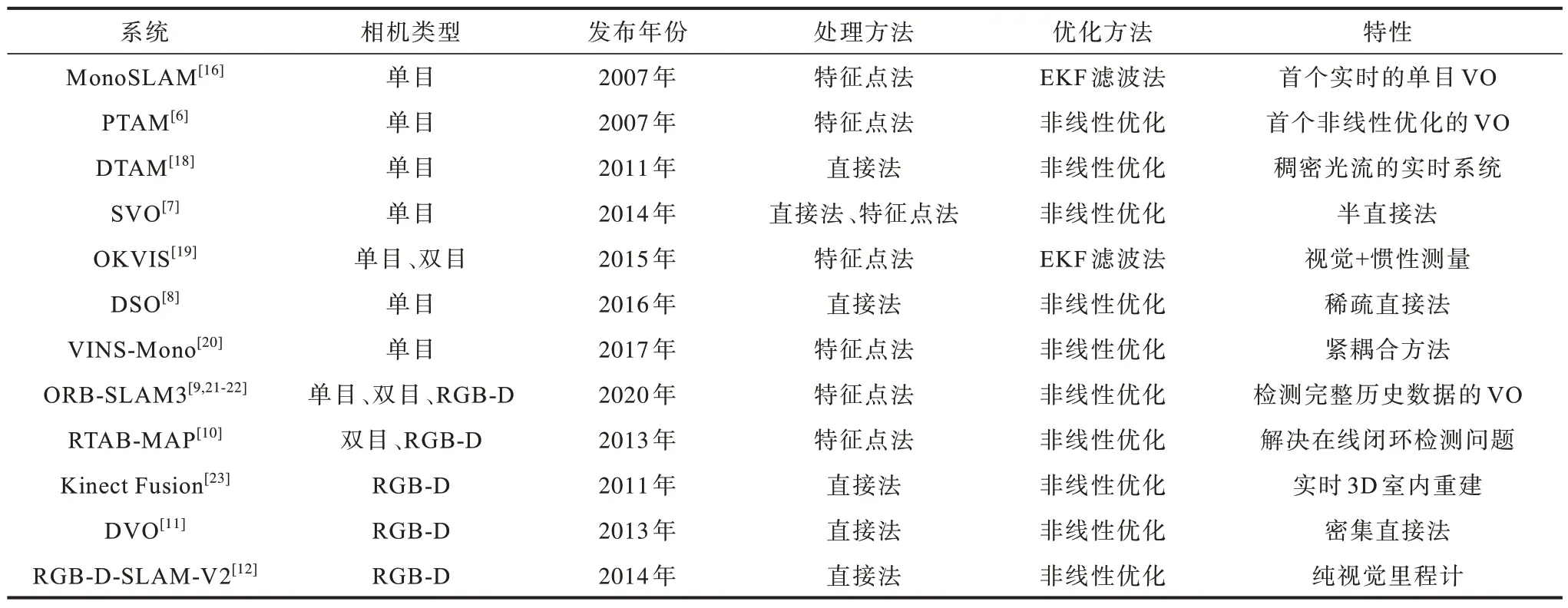
表1 基于传统方法的VO 系统性能对比结果Table 1 Performance comparison results of VO systems based on traditional methods

1.3 特征点法

基于特征点法的VO 系统主要包含特征模块和位姿估计两大部分。其中：特征模块主要包含特征检测、特征匹配、特征误匹配处理；位姿估计通常分为2D-2D、3D-3D、3D-2D。

1.3.1 特征模块

特征模块各部分具体如下：

1）特征检测。特征点由关键点和描述子2 个部分组成。关键点是指特征点在图像中的位置，其具有尺度、方向等信息，在关键点周围的区域生成一个标示性的向量来表示这个区域的特征，这个向量被称为描述子，其作用是将自己与其他区域分开，通常作为匹配过程的基础。

在特征点检测中，角点检测是最早被提出的特征点检测方案之一，角点及其特征在视角发生较大变化时依然能够稳定存在，并且与邻域相差较大。Moravec 角点检测算法［24］以像素点为中心，检测该点与周围一定范围内信息的相似性，不相似则该点会被认为是角点，但该方法具有对噪声和边缘敏感的缺点，而且不具备旋转不变性。Harris 算法［25］在Moravec 算法的基础上使用泰勒展开式，覆盖了所有方向的检测，克服了Moravec 只检测45°倍角的缺点，不仅对噪声不敏感，而且在不同光照条件下均具有很好的稳定性，但该方法不适用于对尺度变化要求较高的场景。Shi-Tomasi 算法［26］进一步优化了Harris 算法，提高了角点的稳定性。从本质上讲，Moravec 算法［24］、Harris 算法［25］、Shi-Tomasi 算法［26］都是基于梯度的检测算法。ROSTEN 等［27］于2006 年提出了FAST 算法，该算法将FAST 角点定义为：若某像素与周围邻域内足够多的像素点差异较大，则该点可能是角点，其具有计算速度快、效率高的特点，在实时场景中可以被广泛应用。

LOWE 等［13］于1999年提出了尺度不变特征变换（Scale-Invariant Feature Transform，SIFT）算法，并在2004 年对其进行改进。SIFT 特征是图像的局部特征，其描述符具有尺度不变性，能够适应旋转、尺度缩放、亮度等变化，具有很强的稳定性和抗干扰性，但随之带来的是极大的计算量，因此，无法实时计算SIFT 特征。BAY 等［14］于2006 年提出了加速稳健特征（Speeded Up Robust Features，SURF）算法，该算法基于SIFT，但改变了其原有的特征点检测方式，并将描述子从128 维降为64 维，解决了SIFT 特征计算量大的问题，提升了算法的执行效率。随后，BRIEF 算法［28］的提出大幅简化了描述子的计算过程，其利用局部图像邻域内随机点对的灰度值来建立特征，生成二值特征描述子，使得特征提取的过程大幅加速，算法实时性较好，但其缺点是不支持大角度的旋转。ETHAN 等［15］于2011年提出了ORB（Oriented FAST and Rotated BRIEF）算法，该算法在特征提取部分用改进的FAST 算法，特征描述部分基于BRIEF 算法进行改进，解决了其原先不适应大旋转角的问题，因此，ORB 算法不仅具备FAST 和BRIEF 速度快的特点，还具有较好的尺度和旋转角度不变性。

2）特征匹配。在检测出了特征点之后，就可以通过匹配算法将图像之间的特征点一一对应起来，这个过程称为特征匹配。特征匹配是VO 中极为关键的一步，它解决了VO 中的数据关联问题，即确定当前看到的路标与之前看到的路标之间的对应关系。通常最简单的特征匹配方法是暴力匹配（Brute-Force Matcher），由于描述子距离代表了2 个特征点之间的相似程度，该算法中将每一个特征点与其他待匹配的特征点进行描述子距离计算，然后在其中寻找最合适的特征点作为匹配点。在实际应用中，也会用到不同的距离度量范数，其中，欧氏距离适合浮点类型描述子，而对于二进制描述子，通常使用汉明距离。暴力匹配算法在特征点数量很多时会出现计算量很大的问题，难以满足实时性需求，因此，研究人员引入近似最邻近（Approximate Nearest Neighbor，ANN）搜索，其适用于匹配点数量极多的情况，在保证匹配精度的情况下大幅提升了匹配速度。MUJA等［29］提出快速近似最邻近（Fast Library for Approximate Nearest Neighbors，FLANN）算法，该算法依据KD 树实现，从已知数据集中的分布特点和其要求的空间资源消耗来给出合理的搜索参数，FLANN 要求的特征空间通常是n维实数向量空间Rn，其依据欧氏距离寻找实例点附近最近的点作为关键点。

3）特征误匹配处理。在实际特征匹配过程中，会遇到误匹配的情况，即将非对应的特征点作为匹配点。误匹配通常分为2 种情况进行处理：

（1）对于几何约束是参数化的情况，随机抽样一致（RANSAC）算法［30］是当前使用最广泛的误匹配点剔除算法，其具有随机性和假设性，可以从一组包含离群数据的数据集中通过迭代方式估算出数学模型参数，但该算法是一种不确定的算法，因此，为了提高结果的精确性，只能提高迭代次数。RANSAC 算法具有结构简单、鲁棒性强的特点。

（2）对于几何约束是非参数化的情况，适合应用向量场一致（Vector Field Consensus，VFC）算法［31］进行处理。该算法的原理是利用向量场的光滑先验，将外点从样本中区分出来，其具有鲁棒性强和匹配率高的特性，对于误匹配率较高的图像效果尤为显著。

1.3.2 位姿估计

位姿估计即计算2 帧图像之间的运动估计，用数学模型表达可以理解为变换矩阵T的计算。在实际运用中，根据特征点类型的不同，位姿估计通常分为2D-2D、3D-3D、3D-2D 这3 类计算方法，具体如下：

1）2D-2D（对极几何）。在单目相机中，通常采集到的信息是以二维图像形式存在，在进行2 帧之间运动估计时，由于图像上的二维点没有做三维测量，因此需要用到对极几何（Epipolar Geometry）。对极几何描述了同一场景在2 幅图像之间的视觉几何关系，其模型如图2 所示。

图2 对极几何约束模型Fig.2 Epipolar geometry constraint model

在对极几何约束模型中，I1和I2代表相邻图像帧，O1、O2是相机中心，设p1、p2分别为I1和I2中已匹配成功的特征点，连线O1p1和O2p2在三维空间中相交于P点，O1O2的连线与I1、I2相交于极点e1、e2，p1e1、p2e2被称为极线。根据代数几何关系，可以得到特征点之间满足以下约束关系：

其中：F是基础矩阵；p1、p2为特征点在图像中的像素位置。通过式（3）可以得出基础矩阵F，基础矩阵F与本质矩阵E存在如下关系：

其中：K为相机的内参矩阵。从式（4）可以得出本质矩阵E，而E=t^R，根据式（5）可求得R和t，即求出了变化矩阵T。

其中：x1、x2为特征点的归一化坐标。

在等式E=t^R中，由于R和t各有3 个自由度，故t^R共有6 个自由度。本质矩阵是由等式为零的对极约束定义的，因此，E在不同尺度下是等价的，即E实际上有5 个自由度，这表明至少需要通过5 对点才能求解相机的运动［32-34］。除此之外，还有6 点算法［34］、8 点算法［35-36］，6 点算法相比于5 点解决方案更加简单，可以更加稳健地估计本质矩阵，且在平面场景中不会失效；8 点算法是从8 个或更多匹配点中通过对匹配点的坐标进行归一化处理来计算基本矩阵，具有简单易实现的优点。在特殊情况下，当相机只做平面运动时，运动模型就会降为3 个自由度，这种情况下仅需要2 对点就能计算出相机的运动参数［37］。

2）3D-3D（ICP）。3D-3D 是针对立体视觉，从三维图像信息中计算位姿估计。假设有一组已经匹配成功的3D 特征点（已经对2 个RGB-D 图像进行了特征匹配）：P={p1,p2,…,pn}，P'={p'1,p'2,…,p'n}，通过对应的特征点求其欧式变换的R和t时，通常用迭代最近点（Iterative Closest Point，ICP）算法［38］求解，而ICP 的求解方式分为2 种，即利用线性代数的求解和利用非线性优化的求解。2 种求解方式具体如下：

（1）在线性代数求解方法中，以奇异值分解（Singular Value Decomposition，SVD）法为代表。根据对匹配点的定义，设第i对点的误差项为：

然后构建最小二乘问题，求出使得误差平方和达到最小的R和t：

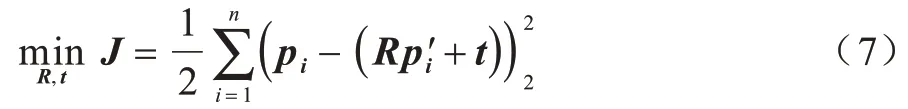
（2）在非线性优化求解方法中，通常使用迭代的方式求最优解。该类方法至少需要3 对非共线的三维点，且与3D-2D 的非线性解法类似，用李代数ξ表示相机位姿，如式（8）所示，通过多次迭代就可找到合适的ξ。

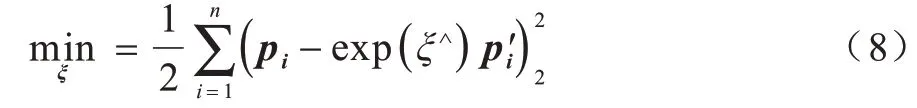
3）3D-2D（PnP）。在求解从三维空间点到二维平面点对的运动估计时，通常使用n点透视投影（Perspective-n-Point，PnP）方法，该方法不需要对极约束，且在匹配点对很少的情况下仍可获得较好的运动估计。

求解PnP 问题有很多方法，包括P3P［39］、直接线性变换、非线性优化等。其中：P3P 方法主要使用3 对匹配点和1 对验证点来估计变换矩阵；直接线性变换则要求最少有6 对匹配点才可实现对变换矩阵T的线性求解，当匹配点大于6 对时，还可以使用SVD 方法对超定方程求最小二乘解；非线性优化法则将PnP 问题构建成一个定义在李代数上的非线性最小二乘问题并进行求解。二维点坐标与空间点坐标的投影关系是求解PnP 问题的关键，其计算过程如下：

其中：P为空间坐标；u为投影的像素坐标。由于相机位姿未知，并且观测点存在噪声，故式（9）方程存在误差，因此需要构建一个最小二乘问题，使得误差最小，然后找出最合适的相机位姿：

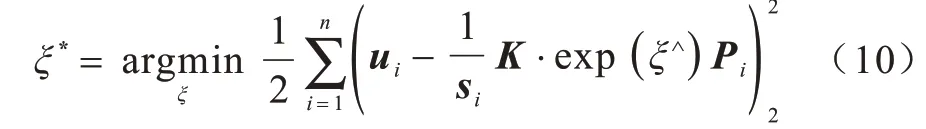
式（10）的误差项是三维空间点根据当前估计投影到二维空间的坐标与观测到的二维真实坐标之间的误差，即PnP 问题可以看作一个最小化重投影误差的问题。

1.4 直接法

在特征点法中，假设特征点是固定在三维空间中不动的点，通过最小化误差来优化相机运动，而在这个过程中，需要精准地知道2 个对应的特征点在相机坐标系下的坐标，这也是进行特征匹配的原因，但由此带来了巨大的计算量。而在直接法中，并不需要知道点与点之间的对应关系，在图像有像素梯度的情况下，仅利用图像的像素灰度信息，通过最小化光度误差来计算运动变化，该方法不要求图像中有特征点，避免了特征点的提取和匹配，同时能够充分地使用图像信息，尤其是在特征缺失的场景中，直接法的效果优于特征点法。

相比于只可以构建稀疏地图的特征点法，直接法还可以构建稠密地图。通常根据像素的使用数量将直接法分为稀疏、稠密、半稠密3 种方法。当P点来自于稀疏特征点时，称之为稀疏直接法，经典的稀疏法有SVO 算法［7］；当P点来自部分像素时，称之为半稠密直接法，如LSD-SLAM 算法［40］；当P点来自于所有像素时，称之为稠密直接法。

直接法是基于灰度不变假设而提出的方法，但是实际情况并不如此，比如相机的自动曝光可能会改变灰度差异，使算法失效。此外，直接法只适用于运动变化很小的情况，很难对较大变化的运动进行位姿估计，并且其在闭环检测过程中存在的累计漂移问题一直没有得到很好地解决［8］。

1.5 直接法与特征点法的对比

目前，基于特征点法的VO 系统依旧占领主流地位，但是在某些特定的场景中，使用直接法效果优于特征点法，如在特征点稀少且有像素梯度时更适合直接法。表2 所示为直接法和特征点法的性能对比结果。

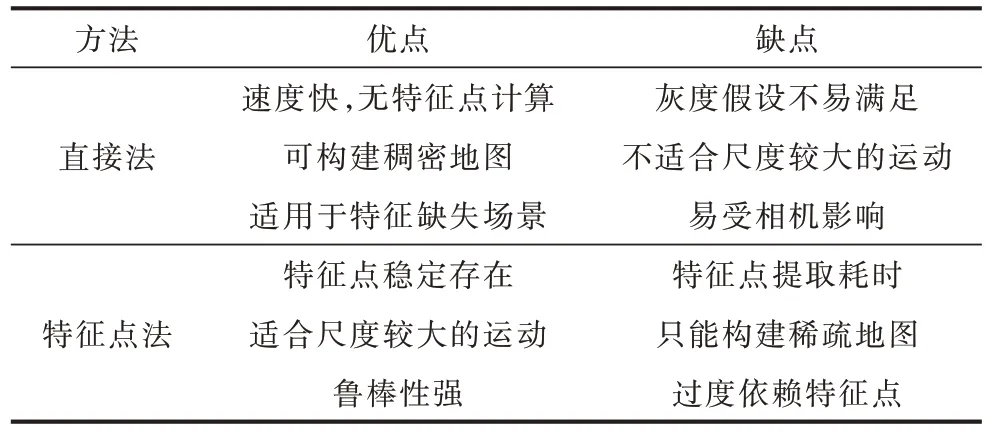
表2 直接法与特征点法性能对比结果Table 2 Performance comparison results of direct method and feature point method

1.6 传统方法的不足

特征点法和直接法这2 种VO 方法已发展多年，但仍面临以下问题：

1）人工设计的特征会丢失图像中大部分信息，在某种程度上会导致VO 效率低下。

2）特征提取计算复杂耗时。

3）在相机运动幅度较大时，特征跟踪容易丢失。

4）对于动态场景处理仍不理想，如视觉画面中有行人持续走动的情况。

5）对光照敏感，在光照条件恶劣的条件下鲁棒性差。

6）在图像特征不明显的情况下会导致精确度降低，并随之引发误差累积。

2 基于深度学习的VO 方法

2.1 方法介绍

近年来，深度学习的发展极大促进了计算机视觉的相关科学研究，提高了视觉相关任务的准确率、鲁棒性以及执行效率。不同于传统VO 系统通过严格几何理论方法来实现的方式，基于深度学习的VO则通过寻找数据规律与目标任务之间的函数关系来完成同样的工作。基于深度学习的VO 主要分为有监督、无监督、半监督3 种学习方法，其中具有代表性的VO方案有DeepVO［41］、GeoNet［42］、CNN-SLAM［43］等。

2008 年，ROBERTS 等［44］首次尝试将机器学习的方法用于VO 系统，通过使用K-邻近（K-Nearest Neighbor，KNN）算法学习从稀疏光流到平台速度和旋转速率的映射，虽然在当时无法像传统几何方法那样准确地进行运动估计，但该方法可以在没有相机校准或场景结构模型的情况下，验证相机和环境的属性与运动估计之间映射的可能性。

基于特征点法和基于深度学习的VO 方法在理论框架上具有一定程度的一致性。其中多数方法都更倾向于使用基于卷积神经网络（Convolutional Neural Networks，CNN）的特征提取网络，相比传统方法其稳定性和匹配准确率更高。2015 年，KONDA 等［45］提出一种端到端的深度卷积神经网络模型来进行位姿估计，虽然在当时其性能与传统方法无法相提并论，但该模型进一步验证了基于深度学习的VO 具有相当的潜力和可行性。2016 年，COSTANTE 等［46］提出一种名为P-CNN VO 的VO 系统，该系统在模糊、亮度对比异常的情况下具有较强的鲁棒性。2017 年，MULLER 等［47］提出了Flowdometry 系统，该系统将原始光流直接作为预测网络的输入，再通过全连接层计算出位姿估计，其达到了同时期同类方法中的最佳性能。2018 年，LIN 等［48］提出一种基于循环卷积神经网络（Recurrent Convolutional Neural Network，RCNN）的全局位姿估计网络模型，该模型主要解决VO 的远距离漂移问题。同年，JIAO 等［49］提出一种端到端的双向循环卷积神经网络的单目VO 系统Magic VO，该系统基于CNN 和双向LSTM（Bi-SLTM），用于解决单目视觉测距问题。2018 年，YU等［50］提出DS-SLAM 系统，该系统将语义分割网络与运动一致性检查方法相结合，减少了动态目标的影响，从而大幅提高了在动态环境中的定位精度。2019 年，ALMALIOGLU 等［51］提出了基于生成式对抗网络（Generative Adversarial Network，GAN）的模型来学习图像特征，通过无监督学习得到一个名为GANVO 的单目VO 系统，该模型相比于监督学习不需要大量的标定数据，且相比于当时大多数的传统方法具有更好的性能。PANG 等［52］提出一种名为CLOCs（Camera-LiDAR Object Candidates）的多模态学习网络，该网络对图像数据集和雷达数据集进行双模态学习，相比于单模态的纯视觉学习，其在精度和鲁棒性上都有了显著提升，并且在KITTI 数据集中达到了较好效果。2020 年，YANG 等［53］提出了D3VO，该系统设计一个自监督单目深度估计网络，提高了前端追踪和后端非线性优化的性能，在单目VO 中，其测试结果相对传统sota 方法得到显著提升。表3 所示为部分基于深度学习的VO 系统的性能对比结果。

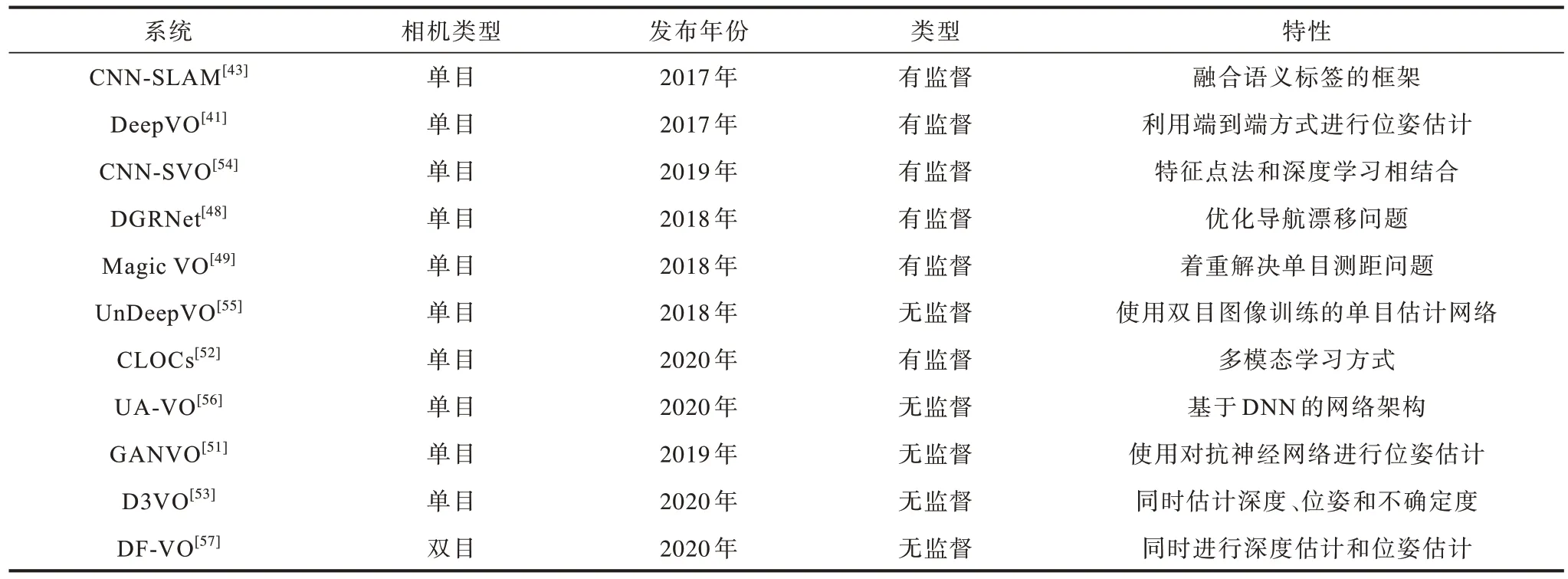
表3 基于深度学习的VO 系统性能对比结果Table 3 Performance comparison results of VO systems based on deep learning

2.2 基于深度学习的VO 方法优点

基于深度学习的VO 相比于传统VO 的性能优势主要体现在以下5 个方面：

1）基于深度学习的VO 系统具有很强的泛化能力，可以在光线复杂的环境中工作。

2）对于动态场景的识别更加有效。

3）采用数据驱动的模型，更符合人类与环境的交互方式。

4）深度学习的方法可以更好地和其他传感器数据融合。

5）端到端的系统省去了中间的复杂流程，直接输出结果。

2.3 基于深度学习的VO 方法缺点

虽然基于深度学习的VO 在一定程度上展现出性能优势，但其依旧存在以下发展瓶颈：

1）模型训练时间长，且需要大量的计算资源。

2）网络层数多的模型容易出现梯度消失问题，使得梯度无法从输出层传到输入层，进而导致训练难度增大。

3）深度学习是典型的黑箱算法，没有理论依据，不像传统方法那样每个环节都有很强的解释性，其通过数据驱动的方式去学习，模型复杂，通常包含上亿个参数，若应用结果出现问题很难确定是哪个参数的原因，从而无法针对性地解决问题。

4）大部分模型依赖于大规模带有标签的训练数据，人工标注数据将消耗大量精力，并且实际场景更具复杂性，不可能收集到所有的标签信息。

5）对数据集要求较高，即使在某个数据集上取得了优秀的结果，换个场景可能导致精准度降低，只有当数据集足够大时，才可能展现出较强的适应性，因此，数据集的大小对于深度学习是一个非常重要的因素。

3 数据集

在测试VO 系统性能时，通常通过公共数据集来对比不同方法的性能，当前在VO 领域比较流行的公共数据集包括KITTI［58］、TUM RGB-D［59］、EuRoC［60］等。表4 所示为不同数据集之间的特性对比结果。

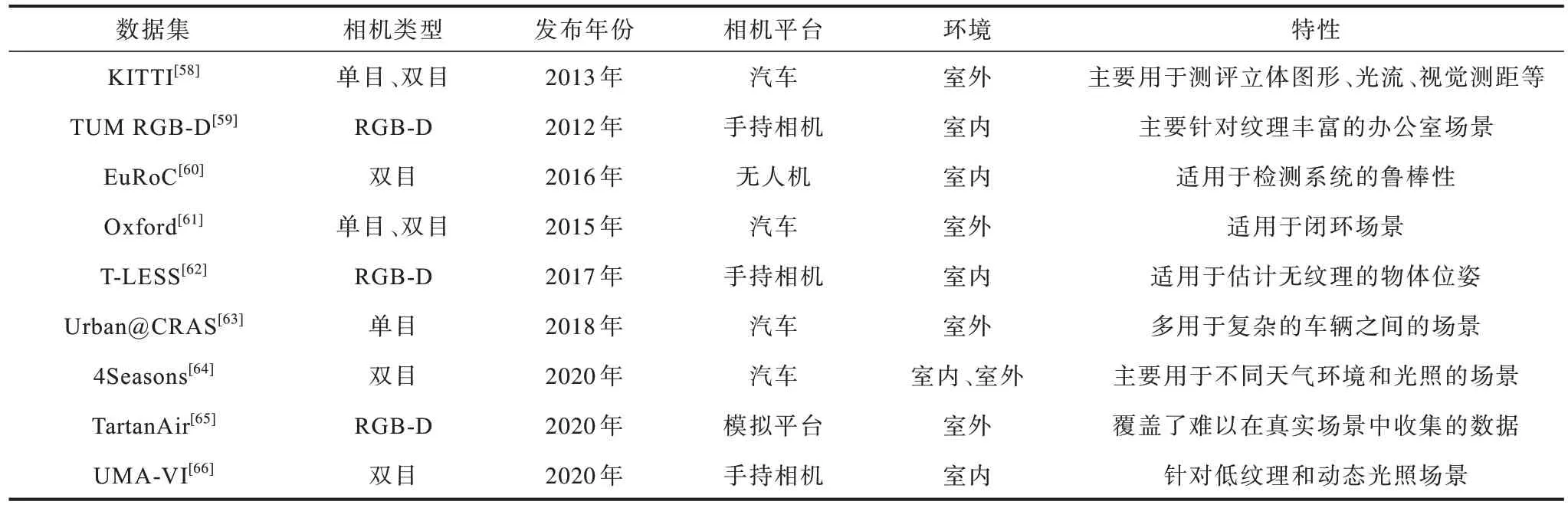
表4 部分VO 数据集对比结果Table 4 Comparison results of some VO datasets

KITTI［58］由卡尔斯鲁厄理工学院和丰田美国技术研究院共同创办，是目前国际上最大的自动驾驶场景下的计算机视觉算法评测数据集，其包含市区、乡村、高速公路等不同场景以及在不同车速和光照条件下的数据，主要面向室外，多用于评测立体图像、光流、视觉里程计、3D 物体检测、3D 跟踪等计算机视觉技术在车载环境下的性能。表5 所示为5 种典型VO 系统在KITTI 上的测试结果。

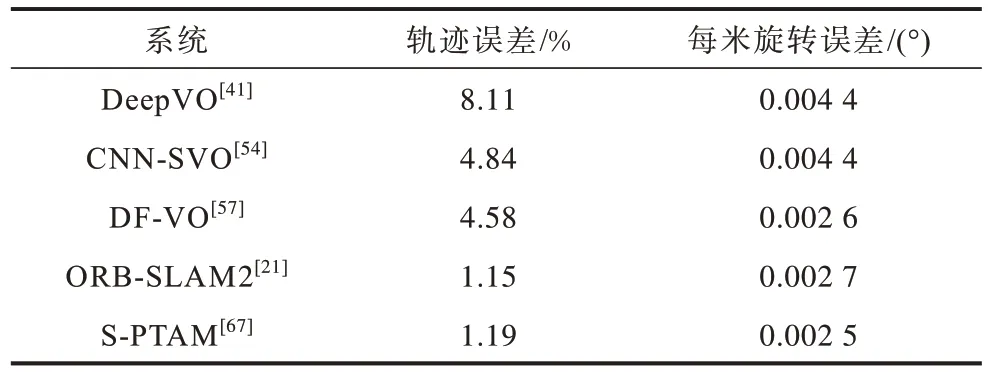
表5 5 种VO 系统在KITTI 数据集上的性能测试结果Table 5 Performance test results of five VO systems on KITTI dataset

TUM RGB-D［59］是由德国慕尼黑工业大学Computer Vision Lab 发布的针对深度相机的数据集，是业界很有名的RGB-D 数据集，该数据集主要针对纹理丰富的室内场景，数据类型多样，包括帧数大小、相机运动快慢、场景结构以及不同的纹理类型。

EuRoC［60］是由苏黎世联邦理工学院发布的一个专门针对室内场景的数据集，其通过小型无人机+双目相机+IMU 的形式采集数据，该无人机运动比较剧烈，适宜于检测系统的鲁棒性。

4 VO 领域未来的研究方向

VO 技术已经发展多年，在很多方面都取得了重大进展，但目前仍旧有一些问题等待解决，本文在总结现有方案的基础上提出以下2 个值得探索的研究方向：

1）提高VO 在动态场景下的鲁棒性。动态场景中存在着不确定因素，如在分辨动态物体时还要处理被遮盖的静态场景，而且许多VO 方法只能容忍在小尺度动态场景内发生的部分异常事件，在大尺度动态场景中并不能达到很好的效果。为了实现场景由小范围固定环境到大范围复杂动态环境的扩展，保证VO 在动态场景中具有良好的环境适应能力，需要快速有效地处理动态场景，这也是VO 未来的研究热点。

2）探索基于深度学习的多模态融合VO 框架。机器人在移动过程中会面临诸多场景变化，如天气季节、光照角度、动态遮挡等，纯视觉的单模态系统易受噪声影响，从而降低轨迹估计的精确度。多模态融合的系统常使用多种传感器来补偿位姿估计，从而降低场景变化时所带来的噪声影响。如使用IMU 提高高速运动下的定位效果，使用LiDAR 提高不良照明条件下的鲁棒性。同时，深度学习模型能充分利用不同类型传感器的信息，提高对各类信息的利用率。因此，基于深度学习的多传感器融合VO框架是一个值得探索的课题。

5 结束语

VO 方法在移动机器人领域应用越来越广泛，本文分别介绍基于传统几何和基于深度学习的2 类VO 方法，并对比分析各类经典方法的性能特点，总结当前在VO 领域常用的公共数据集。分析结果表明，在VO 领域，以特征点法为代表的传统几何方法依旧是当前较为可靠的解决方案，同时基于深度学习的VO 也在不断地展现出新的成果，虽然后者在VO 的部分环节表现出比传统方法效果更好的特点，但其整体性能和传统几何方法相比还有差距，依旧存在较大的发展空间。实际应用场景复杂多样，下一步将针对弱纹理环境中的特征提取问题进行研究，引入线特征策略来提高特征提取的精确度，同时尝试使用深度学习方法优化前期的图像数据，从而提高图像质量。