基于中断概率的星地网络鲁棒功率控制算法

陈威龙，梁 俊，肖 楠，郭子桢

（空军工程大学 信息与导航学院，西安 710077）

0 概述

星地网络作为实现全球无缝覆盖的重要组成部分，能够使卫星网络［1］和地面网络形成有效互补与互连互通，是下一代卫星通信技术发展的主要趋势［2］。随着地面网络业务传输需求的不断增多，卫星通信与地面通信对频谱的竞争日益激烈，频谱干扰问题成为制约星地网络发展的主要因素［3］。认知无线电技术是一种提高频谱利用率的有效手段，如何将卫星链路长时延、大衰落等特点与认知无线电相结合，成为卫星通信研究机构的关注焦点［4］。

在认知无线电中，减少频率干扰的关键是功率控制技术，因此，星地认知网络中的功率控制得到了国内外学者的广泛关注。文献［5］采用基于投影梯度的动态博弈模型，通过纳什均衡方法提高了频谱利用率，但前提是基于完美信道感知信息的情况，通常网络难以得到精确的系统参数。文献［6］联合考虑能量消耗，对信道选择和控制进行联合优化，但是没有考虑卫星信道的时变特性。文献［7］考虑功耗和接收到的信干比，提出一种鲁棒的功率控制算法，但是没有考虑感知存在延迟的情况。文献［8］引入一种特殊的约束条件优化上行链路，但是没有考虑次级用户间公平性的问题。文献［9］考虑网络的能效和平均吞吐量，提出联合确定最优功率和帧长的低复杂度算法，但是没有考虑因网络拓扑或信道的变化而产生的中断问题。文献［10］根据距离提出动态调度的功率分配策略，但不足是需要精确感知每个用户的位置。文献［11］考虑信道信息感知的不确定性，提出一种鲁棒的资源分配方案，但是能量效率较低。文献［12］提出一种低复杂度的中继选择和功率分配联合优化算法，但是没有考虑因授权用户行为变化而导致中断的情况。

目前，多数星地网络功率控制算法仍基于完美信道信息感知情景，没有考虑卫星网络中因覆盖范围大而产生中断的情况。此外由于卫星网络用户大多为移动用户，因此能量消耗也是需要解决的问题。本文考虑信道转移概率的不确定性，提出信道状态似然不确定性模型，并进一步构建信道状态离散马尔科夫链。在此基础上，采用鲁棒的向后递归方法得到功率分配矩阵，利用博弈论方法设计基于中断概率的星地网络鲁棒功率控制算法。

1 问题模型

1.1 系统模型

本文在静止轨道卫星点波束覆盖场景下建立星地认知网络模型，如图1 所示，网络中包括N个认知用户（Secondary User，SU）和M个授权用户（Primary User，PU）。假设每个授权用户信道只允许一个认知用户进行通信，认知用户采用定向天线与卫星进行通信，卫星传输链路采用Generalized-K 模型［13］。

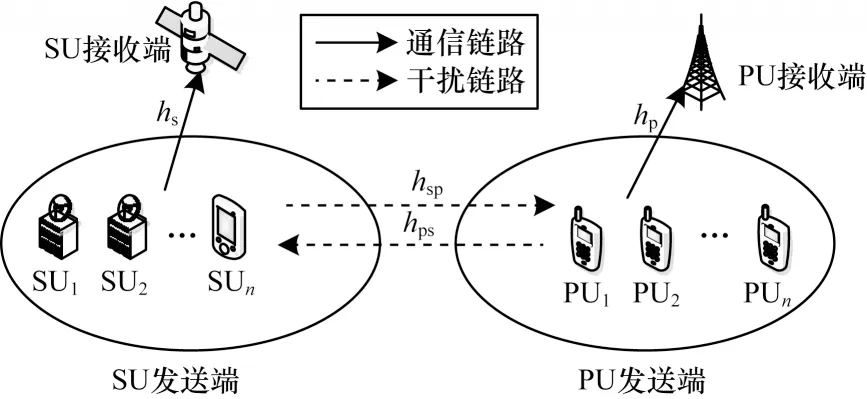
图1 星地认知网络模型Fig.1 Satellite-ground cognitive network model

在信道模型中，视距分量和多径分量的幅度均服从Nakagami-m分布，接收信号功率的概率密度函数为：

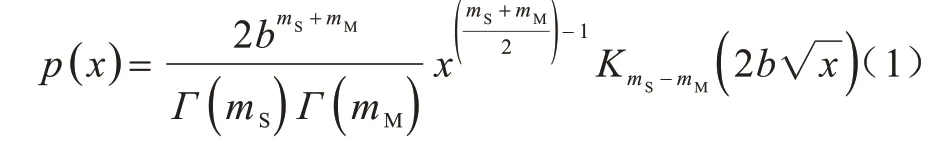
其中：x>0；KmS-mM(∙)是第2 类修正贝塞尔函数，阶数为mS-mM，mM≥0.5，mS≥0，分别为多径参数和阴影参数为接收信号的平均功率。

卫星用户到卫星的通信链路增益为hi，地面用户到卫星用户的链路增益为hp，则第i个认知用户的信干比为：

1.2 马尔科夫决策模型

采用图2 所示的离散时间马尔科夫链对PUm行为建模，由一组离散状态S={s0,s1,…,sK-1}表示，其中：K是状态总数；s0表示PUm处于活动时的状态；s1,s2,…,sK-1表示PUm处于不活动时的状态，在此状态下，PUm不同的状态影响SUi的信干比，因此，用SUi的信噪比阈值来确定PUm的各个状态［15］。

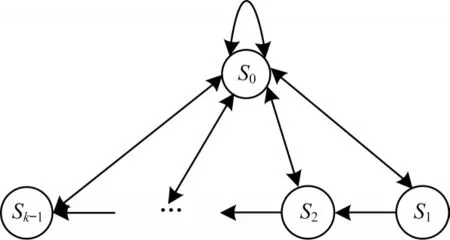
图2 离散时间马尔科夫链Fig.2 Discrete time Markov chain

对于马尔科夫链各个状态sk做如下规定：

1）当k=0 时，活动状态s0可以转变为任何状态。

2）当1≤k≤K-1 时，每个不活动状态sk只能转换为相邻状态或活动状态，即sk→sk-1/sk+1/s0。

以Pkj表示从状态i到状态j的转移概率，以St表示时隙t中的信道状态，有Pkj=P(St+1=sj|St=sk)。将信噪比阈值表示为{Γ1，Γ2，…,ΓK-1}，分别对应于PUm不活动时的各个状态。因此，可以得到PUm非活动状态之间的转移概率［16］，如式（4）所示：

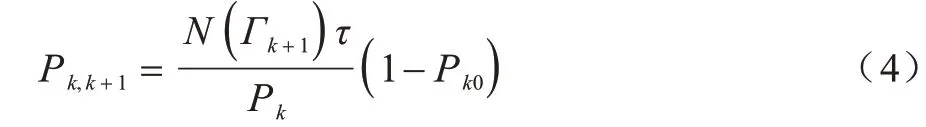
其中：τ是一个时隙的长度；Pk表示信干比落入[Γk，Γk+1]的概率；N(Γk+1)表示电平通过率，其为衡量衰落的关键指标。与此同时，PUm的活动状态（即P0j和Pk0）由PUm自身决定。因此，PUm的状态由转移概率Pkj=P(St+1=sj|St=sk)组成的转移矩阵决定。

当PUm处于活动状态时，规定SUi的最大发射功率为pL。当pi＞pL时，信道会发生中断；另一方面，由于星地认知网络覆盖范围大，存在传输延迟和频谱感知延迟，因此只能在当前时隙t观察到St-t0，其中t0为延迟时间。由此可以得到信道的中断概率为：

为了在延迟存在的情况下实现最优的功率控制，定义时隙t中的中断概率预算Ot，Ot+1=Ot-ot。因此，时隙t中的系统状态Xt≜(St-t0,Ot)，其由时隙t观测到的信道状态St-t0和中断概率预算Ot组 成［17］。令P(Xt+1|Xt,pt)表示转移概率，由于信道状态转移概率与中断概率相互独立，因此有：

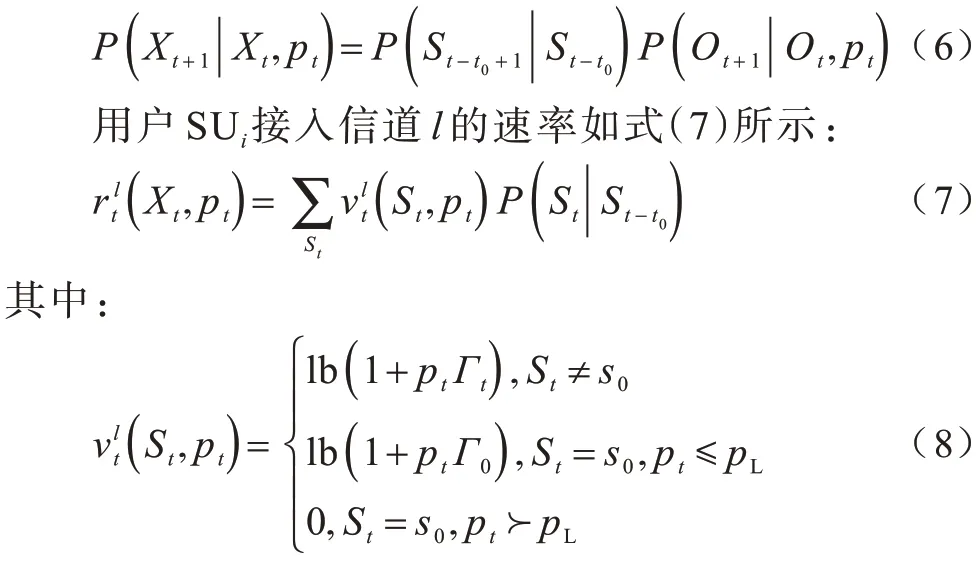
对于接入信道l的用户SUi，功率控制优化目标是不仅实现当前时隙内速率的最大化，同时也实现未来速率期望的最大化。因此，本文优化目标为：

2 鲁棒功率分配策略

对于式（9）所示问题的鲁棒功率分配，应考虑两方面的速率最大化，令时隙t时的未来速率期望和如式（10）所示［18］：

在实际过程中，PU 的行为和信道转移概率模型都难以准确描述，造成功率计算的精确度大大降低，因此，本文考虑鲁棒性来降低模型不确定性的影响。在鲁棒的功率分配问题中，定义信道状态的转移矩阵如式（13）所示：

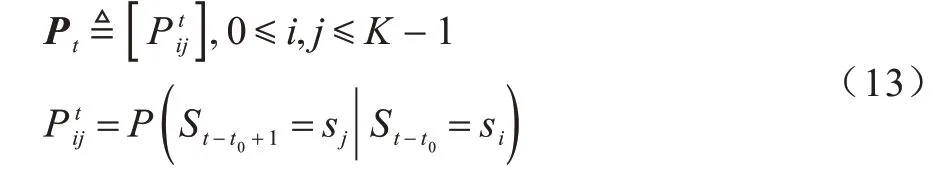
其中：Pt∈Θ，Θ是给定的有界集合。因此，式（9）所示的鲁棒性问题表示为式（14），即考虑信道转移模型最坏情况下的功率分配速率期望和最大化，求解方法是与式（12）类似的向后递归方法。

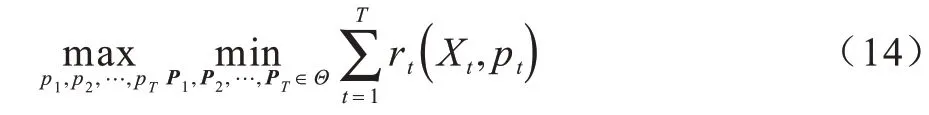
对式（10）～式（12）做简单整理，首先根据转移模型最坏情况下得到速率期望和最小值［19］，如式（15）所示。然后找出使速率期望和最小值最大化的功率分配，如式（16）所示：

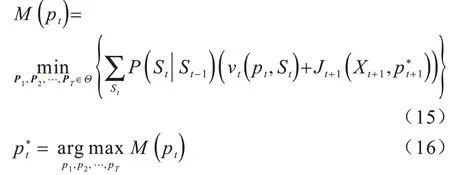
可以看出，求解上述鲁棒功率分配问题的关键在于式（15）的求解，即信道状态的不确定模型，本文采用似然不确定性模型来解决此问题［20］。基于似然不确定性模型的经验转移概率矩阵可以表示为：

其中：P(j)是信道转移矩阵Pt的元素；αi是预先给定的，表示第i行的不确定性水平，取值范围为如式（20）所示：

由于目标函数是线性的，并且约束条件中对pT求二阶导均为非负，容易得到上述问题是凸的，因此采用转换为对偶问题的方法。构建式（23）所示问题的拉格朗日函数，如式（24）所示：

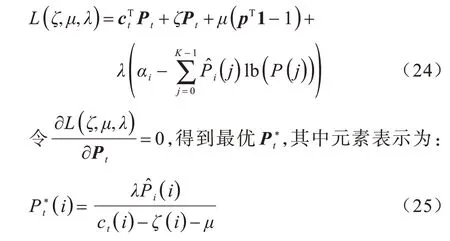
将式（25）代入式（24），得式（23）所示的对偶问题［21］：

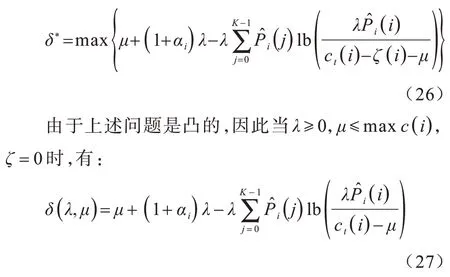
而在其他情况下，δ(λ，μ)→+∞。

为了简化变量，由文献［22］可得：

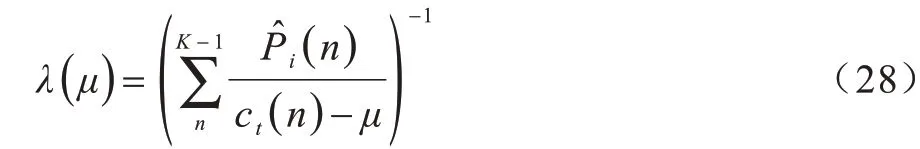
将式（28）代入式（27），即可得到式（23）所示问题的转化问题，如式（29）所示：

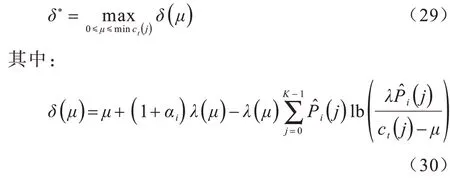
由于已知μ的取值范围，因此可以先求导再采用对分搜索方法［23］求解，得出式（15）所示问题的解，而对于式（16）所示问题，依然采用式（12）的向后递归的方法。

3 基于感知延迟的星地网络功率控制算法

上一节中得到了储存在离线表中的最佳传输策略，而对于多用户的星地认知网络，则需要进行信道选择与功率控制以得到最优的通信质量。本节采用博弈论的方法来进行多用户的资源分配，设计基于感知延迟的星地网络鲁棒功率节能博弈算法RPSGA-SD。

在博弈论中，每个参与博弈的用户都希望自身的效用函数最大化，而在星地认知网络中用户多为移动用户，能量消耗是要考虑的重要问题。因此，定义效用函数如式（31）所示［24］：

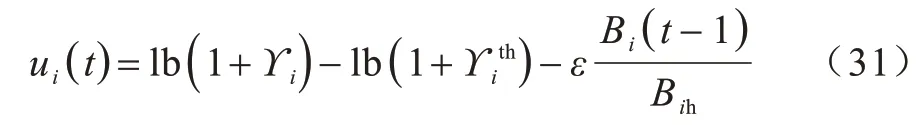
因此，可以实现认知用户SUi的最优功率控制，如式（33）所示：

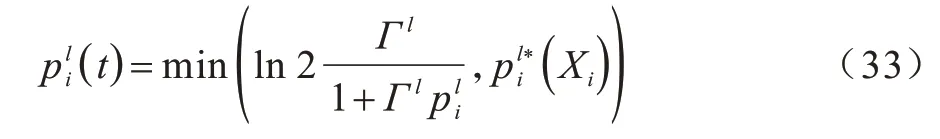
RPSGA-SD 算法流程如图3 所示。

图3 RPSGA-SD 算法流程Fig.3 Procedure of RPSGA-SD algorithm

4 仿真与分析

假设本文星地网络有10个PU用户和5个SU用户，马尔科夫决策模型有10个状态，其中，s0表示活动状态，s1,s2,…,s9表示不活动状态。信噪比阈值设置为Γk=Γk-1+2 dB，Γ0=0。仿真时隙数T=20，最低功率限制pL=0.5 W，功率预算Bih=100 W，信干比门限=1 dB，中断概率预算Oc=0.1，信道延迟t0=2。卫星高度为35 786 km，信道转移概率设置如下：P0j=0.02，j=1,2,…,9，Pi0=0.25，i=1,2,…,9，Pi,i+1和Pi-1,i由式（3）给出。本文选取RRAP 算法［11］和TS-RS-PA 算法［12］作为对比算法，在不同情况下比较3 种算法性能。

总时隙内3种算法在时延t0=2和t0=4时的平均功率和中断概率分别如图4和图5所示。总体来看，随着时隙的增加，用户功率逐渐下降。从图4（a）和图5（a）可以看出：RRAP 算法由于考虑了SU 用户的QoS 需求和延迟，平均功率为三者最高，并且由于信道延迟的增加造成了功率下降；TS-RS-PA 算法将观察到的延迟信道状态近似为当前信道状态，平均功率基本没有变化；RPSGA-OP 算法由于考虑了能量消耗问题，因此平均功率最低。从图4（b）和图5（b）可以看出：由于TS-RS-PA算法忽略延迟状态，因此中断概率最高；而RPSGA-OP算法会考虑所有可能的信道状态，因此中断概率可以满足通信要求。

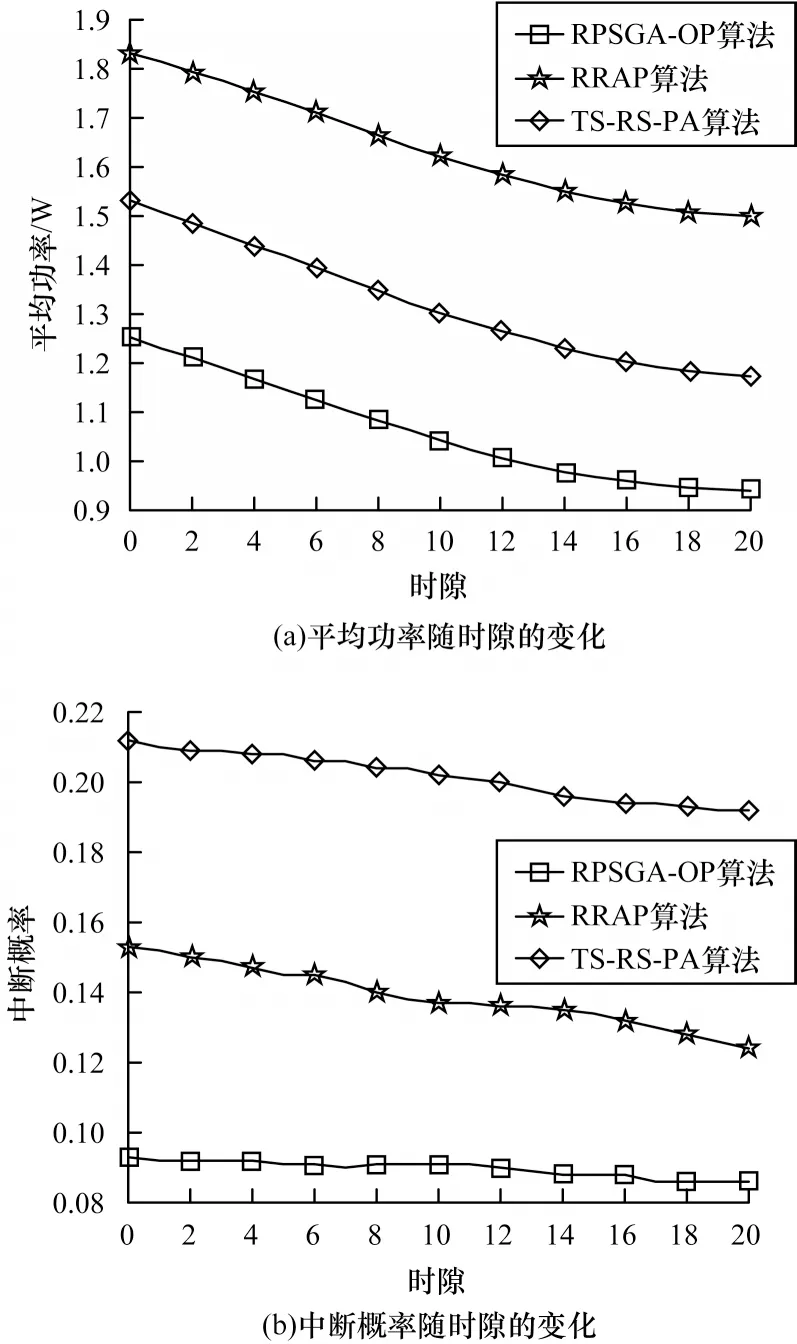
图4 基于网络延迟的算法性能比较(t0=2)Fig.4 Comparison of algorithms performance based on network delay(t0=2)

图5 基于网络延迟的算法性能比较(t0=4)Fig.5 Comparison of algorithms performance based on network delay(t0=4)

在信道状态不确定情况下，总时隙内3 种算法的平均功率和中断概率如图6 所示。定义区间模型不确定度为：

其中，fi(j)表示真实过渡矩阵的元素，图中不确定度是对估计的过渡矩阵和真实过渡矩阵之间误差的量化表示。从图6（a）可以看出，随着信道不确定度的上升，RPSGA-OP 算法为了减少信道不确定性带来的影响，增强系统的鲁棒性，功率逐渐降低，而其他2 种算法功率基本保持不变，由此带来的结果如图6（b）所示，可以看出，RPSGA-OP 算法中断概率还是维持在中断约束内，具有较好的鲁棒性，而其他2 种算法随着不确定度的增加，中断概率不断上升。

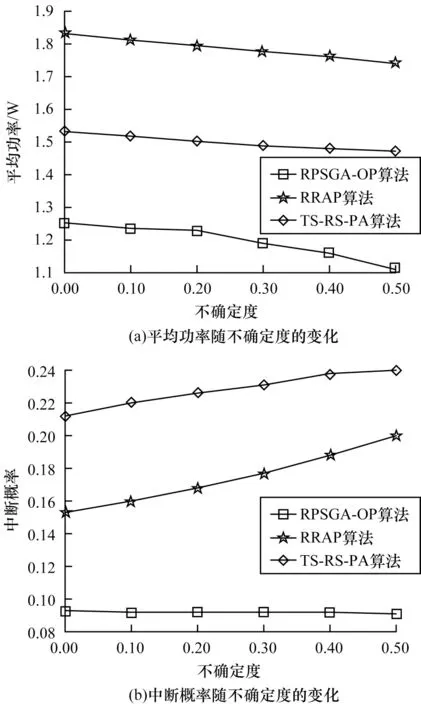
图6 基于模型不确定度的算法性能比较Fig.6 Comparison of algorithms performance based on model uncertainty

总时隙内3 种算法剩余能量的变化如图7 所示，可以看出，RPSGA-OP 算法在博弈过程中由于考虑剩余能量的变化，因此能量剩余最多，达到了节能的目的，而其他2 种算法没有考虑剩余能量，能量消耗相较RPSGA-OP 算法很大。

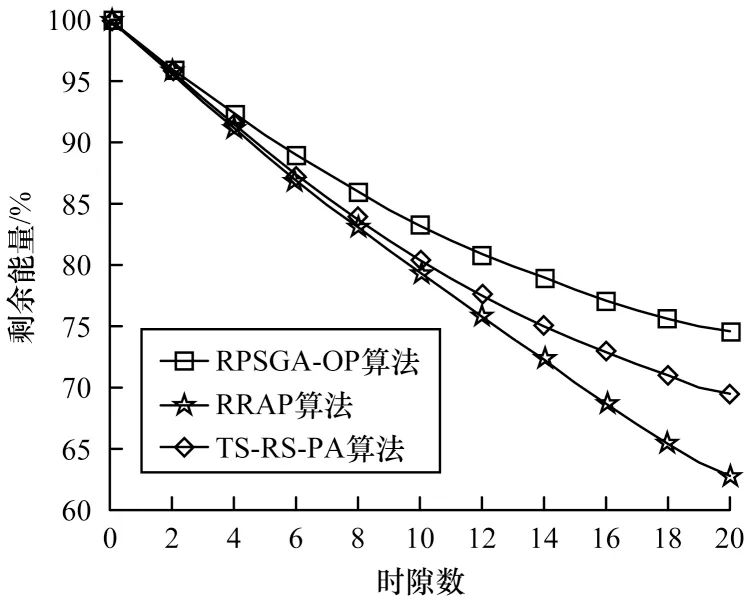
图7 能量消耗随时隙数的变化Fig.7 Energy consumption changes with the number of time slots

5 结束语

本文针对因感知延迟而导致用户通信中断的问题，建立信道马尔科夫决策链表征信道衰落和PU 用户行为，并利用中断约束保护PU 用户传输，考虑模型参数不确定时的鲁棒功率控制，同时针对能量消耗问题采用博弈论方法，使每个认知用户都选择对自身最优的信道。仿真结果表明，在考虑网络延迟的情况下，该方法能够有效降低中断概率，并且其在信道转移模型不确定的情况下也具有较好的性能。下一步将从算法复杂度和收敛速度2 个方面出发设计功率控制算法，更好地满足实际应用要求。