基于智能计算的周转器材消耗预测最优组合模型

柴林，郭峰，熊天霞

（海军航空大学青岛校区，青岛 266041）

引言

周转器材是指日常供应保障的器材。周转器材的种类和数量都很多，也占用了大量的航材保障经费，如何准确地预测周转器材的消耗数量也一直是海军部队航材保障工作中的重点和难点。现有文献中所采用的单项预测方法在周转器材消耗预测精度方面存在一定的不足，会产生较大预测误差，而组合预测方法能够综合利用多种方法，获得更多的有用信息，能够提高预测的精准度和可靠度，在军事、经济等领域得到了广泛的应用。

当前，国内外有很多单项预测方法在航材消耗预测方面的研究，但在航材消耗组合预测方面的研究成果不多。万玉成等人在《航材消耗广义加权函数比例平均组合预测模型》中提出了一种新的组合预测模型——广义加权函数比例平均组合预测模型，并利用二次规划算法求解其加权系数。针对航材消耗的季节性与波动性特点，本文建立了基于灰色系统和神经网络的航材消耗广义加权函数比例平均组合预测模型并以实例说明了其预测效果[1]。毛开翼在《关于组合预测中的权重确定及应用》中运用组合预测模型进行比较，并对组合预测的权重通过几种赋权方法进行综合分析，结合实例对各种预测模型与组合预测模型探讨了不同的组合预测权重的确定方法在实际中的应用。实例表明所提出的组合预测模型比单项预测模型的预测精度高[2]。耿建军等人在《基于GRNN神经网络的变权组合预测的权重确定方法》中为使组合预测的组合权重随样本数据不同而改变，从而使误差平方和达到最小，采用了二次规划法对不同样本数据组合权重进行确定，利用所得权重样本通过广义神经网络训练使其对样本数据组合权重进行确定[3]。

现有研究成果中同时采用多种传统方法和人工智能方法探索在周转器材消耗预测最优组合模型的研究比较欠缺，本文在这方面进行了探索性研究，主要采用了一次指数平滑法、灰色系统预测法、一元线性回归分析法等传统方法和BP神经网络、遗传算法等人工智能方法，建立了航材消耗最优组合模型，并进行了算例分析。下面进行详细介绍。

1 单项预测方法

1.1 一次指数平滑法

设周转器材历年的消耗数依次为：y1,y2,…,yT，α为加权系数，0<α<1，则一次指数平滑预测值为：

初始值的确定：若样本数量较多，如n≥20，初始值对以后的预测数值影响较小，这时可选择将第一个数据作为初始值，也就是若样本数量较少，初始值对以后的预测数值影响较大，这时可选择将最初两期的实际数据的平均值作为初始值，也就是

加权系数的确定：如果已知数据基本趋势较为稳定，波动较小，这时α取值应该小一点，如α=0.2；如果已知数据波动较大，这时α取值应该大一些，如α= 0.8，使预测模型灵敏度高一些。如果已知数据不是很多，可以多取几个α值分别进行计算，选择均方误差小的α值作为实际预测时的加权系数。

1.2 灰色系统预测法

令X(0)为GM（1,1）建模序列：

X(1)为X(0)的1-AGO序列：

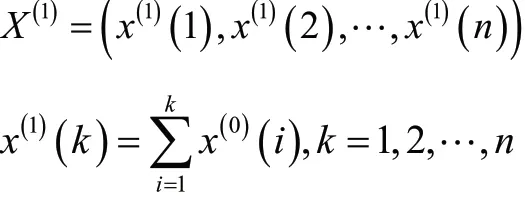
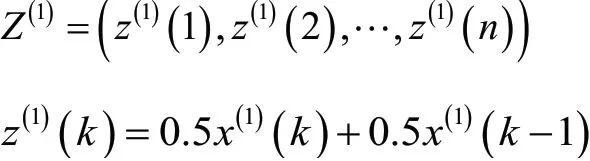
式中：

则灰色系统预测值为：

式中：

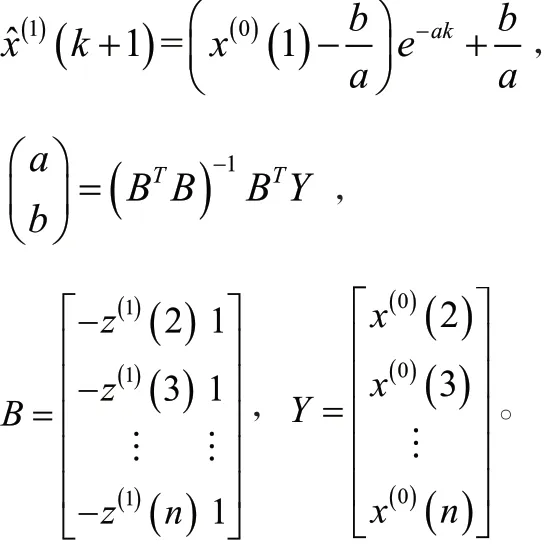
1.3 一元线性回归分析法

设x为自变量，y为因变量，y与x之间存在某种线性关系，则一元线性回归方程为：

式中：

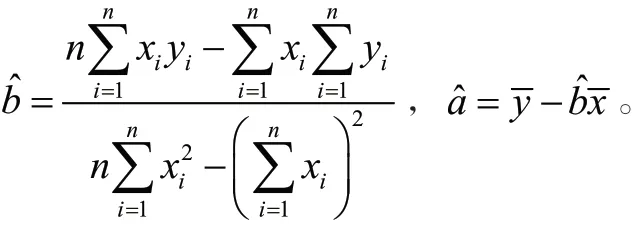
1.4 BP神经网络模型参数设置

设Xi为输入矩阵，kT为输出矩阵，Uij为输入层与隐含层的连接矩阵，Vij为隐含层与输出层的连接矩阵，Yp为期望输出矩阵，i为输入层神经元个数，j为隐含层神经元个数，k为输出层神经元个数。确定最佳隐含层的神经元数j的公式为：

式中：

a—1~10之间的常数[4]。

2 组合预测方法

不同的单项预测方法各有优劣，是相互联系和相互补充的。不同的单项预测方法利用的数据不尽相同，得到的信息也就不尽相同。如果直接将某种预测误差较大的单项预测方法弃置不用，可能会丢失部分有用信息。而如果将不同的单项预测方法进行优化组合，利用不同的单项预测方法提供的不同的有用信息，则可以大大提高预测的精确度。经过优化组合之后的新模型就是组合预测模型。

2.1 模型的建立

设ix为第i种方法的加权系数，Yit为第i种方法第t年的预测值，tY为组合预测方法第t年的预测值，则组合预测模型的目标函数为：

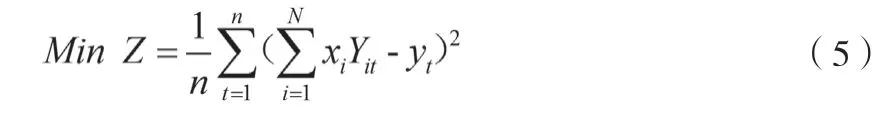
式中：

N—选取单项预测方法的个数。

2.2 加权系数的确定

在组合预测时最重要的就是求出加权系数，使组合预测模型的结果能够更加精确。在求解加权系数过程中，一定要保证所有方法权系数之和为1，也就是同时也要满足 xi≥0这个条件。本文通过遗传算法进行求解，遗传算法的步骤[5,6]如下：

步骤1 ，参数设定。本文取种群数目为200、交叉概率为0.6、变异概率为0.001、进化代数为600、代沟为0.9。

步骤2 ，本文采用实数编码并生成初始种群，个体编码串长度为单项预测方法的数量N。

步骤3 ，根据选择的适应度函数计算种群适应度。由于组合模型的目标函数Z是极小值问题，而在确定遗传算法的适应度函数时，需要将极小值问题转化为极大值问题。

步骤4 ，根据适应度在遗传空间依次进行选择、交叉和变异操作，产生新一代群体。

步骤5 ，返回步骤3，直到达到所设定的进化代数，最后获得组合模型的加权系数。

2.3 模型评价

为了对本文所建立的组合预测模型的准确度进行全方位的综合性评价，按照组合预测效果评价原则和惯例，预测误差一般至少采用三种误差性能指标进行全面评价，并从中选取预测误差最小的一组作为最优组合预测模型[5,6]。本文主要采用了以下三种误差性能指标进行模型评价。

1）误差平方和(Squared Sum Error，SSE)

2）均方误差(Mean Squared Error，MSE)

3）希尔不等系数(Theil IC)

希尔不等系数的取值通常为0到1之间，其值越小则拟合程度越高。

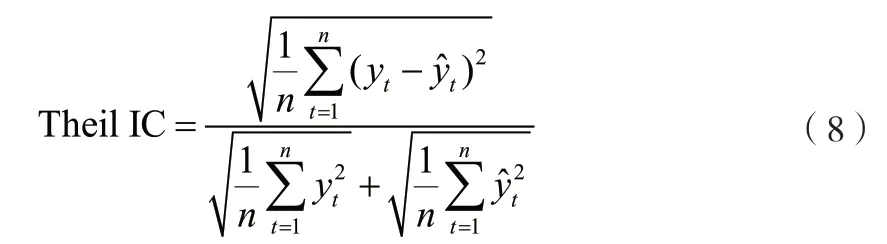
yt—第t年真实的消耗数；

n—样本数量。

3 算例分析

海航某机场航材股某器材历年来的消耗数据如表1所示，预计未来一年的飞行训练时间为120 h，试预测该器材下一年的消耗数量。

表1 海航某机场航材股某器材历年来的消耗数据

采用BP神经网络进行计算时，网络的隐含层神经元数为5，即BP神经网络的最终结构为BP（1，5，1）。不同单项预测方法的三种误差性能指标计算结果如表2所示。

表2 单项预测方法的误差性能指标

在单项预测方法中，根据误差平方和、均方误差计算结果可知，一元线性回归分析法预测效果最好，一次指数平滑法预测效果最差；根据希尔不等系数可知，BP神经网络法预测效果最好，一元线性回归分析法的预测效果近似于BP神经网络法，一次指数平滑法预测效果最差。因此，总体上来说在单项预测方法中一元线性回归分析法精度最高，一次指数平滑法精度最低。这说明一元线性回归分析法考虑的因素更多，因此预测结果也更精确。

与每一种单项预测方法相比，组合预测法的三种误差指标计算值更小，表明组合预测法能够获得单项预测方法所难以获得的精确、稳定的预测结果。

另外，通过遗传算法进行求解的各个单项预测方法的权重如表3所示。

表3 表明，一元线性回归分析法所占权重最大，一次指数平滑法所占权重最小，这与上述不同单项预测方法的误差分析结果完全相符。可见，组合预测能够赋予预测精度高的单项方法更高的权重，如此可以最大限度地从各单项预测方法获得更多更有用的信息。

表3 权重系数表

4 结束语

本文将一次指数平滑法、灰色系统预测法，一元线性回归分析法、BP神经网络法四种单项预测方法建立了周转器材消耗预测最优模型，并通过遗传算法求得其在组合预测方法中的权重系数。本文提出的周转器材消耗预测最优模型综合采用了传统的预测方法以及人工智能方法，算例表明该模型比任何一种单项预测方法的精度都高。本文的研究成果具有较高的现实意义和推广应用价值。