勾股定理——解决实际问题的桥梁
2021-11-18 07:34浦梦婷
初中生世界 2021年42期
文/浦梦婷
一、怎样花钱最少呢?
如图1,A、B两所学校在河l的同侧,分别距离河边1km和3km,两所学校水平距离为3km。现两校准备在河边合建一座水厂,铺设水管的工程费为每千米1万元。请在河边选择一个位置,使铺设水管的费用最低,并求出最低费用为多少。
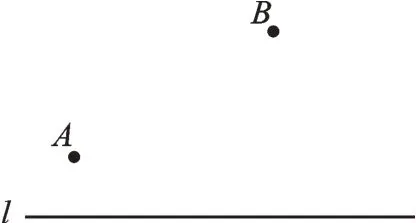
图1
要使得费用最低,则铺设水管距离最短,即在l上取一点D,使得AD+BD最短。这与我们熟悉的“将军饮马”问题类似。同学们可以试着作辅助线,如图2,利用勾股定理求出BC的长,最后求得最低费用为5万元。
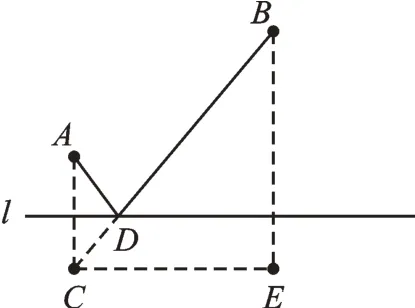
图2
二、地基挖得合格吗?
图3 是农民自建房的地基平面图,按标准应为长方形。工人挖完后测量了一下,发现长为16m,宽为12m,对角线长度为19m,请你帮他看看挖得是否合格。
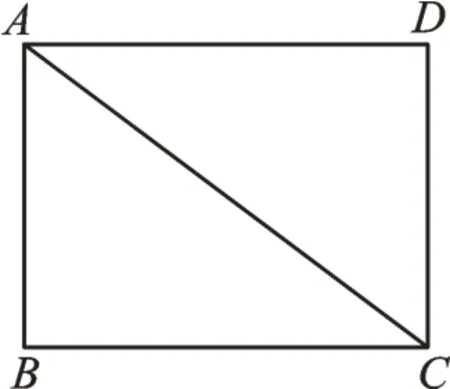
图3
我们可以运用直角三角形判定定理,即勾股定理的逆定理,来验证。由题意得AB=12,BC=16,AC=19,因为AB2+BC2=400,AC2=361,所 以AB2+BC2≠AC2,即∠ABC≠90°,所以工人挖得不合格。
三、木棒能放进木箱吗?
有一根木棒,要放在长、宽、高分别是50cm、30cm、40cm的木箱中,木棒最长为多少?
如图4,木箱的形状是长方体,其空间的最大长度为木箱的对角线的长,即BF或CE。由题意得BC=50,CG=30,FG=40。在RtΔBCG中,BG2=BC2+CG2=3400。在RtΔBGF中,BF2=BG2+GF2=5000,所以BF,即木棒最长为
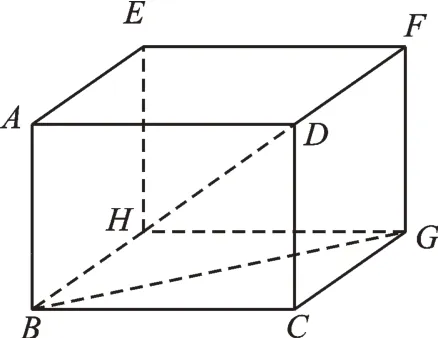
图4
猜你喜欢
小天使·一年级语数英综合(2020年5期)2020-12-16
作文周刊·小学二年级版(2019年21期)2019-08-09
读友·少年文学(清雅版)(2018年7期)2018-11-16
学与玩(2017年7期)2018-03-05
中学生数理化·八年级数学人教版(2016年2期)2016-04-13
中学生数理化·八年级数学人教版(2016年3期)2016-04-13
小雪花·成长指南(2015年7期)2015-08-11
红蜻蜓(2015年1期)2015-03-26
小天使·五年级语数英综合(2014年12期)2015-01-14
读写算·高年级(2009年8期)2009-08-12

