基于分布式协调算法的多导弹网络避障*

杨孝敬，郭 涛，李 娜

（安阳师范学院计算机与信息工程学院，河南 安阳 455000）

0 引言

随着对高自适应制导和控制方法需求的不断增加，对无人机［1］、地面车辆［2］、无人水面车辆［3］、自主水下车辆［4］和移动机器人［5］提出了避障技术。影响导弹精准拦截的条件比较复杂，障碍规避和实际复杂条件对制导和控制系统的要求较高。因此，最近一些研究集中在避障路线［6］和制导策略［7］上。然而，在上述研究中只考虑了单一的拦截导弹，为了提高多节点网络的目标探测和攻防能力，需要实现多节点网络的协同工作［8］。该问题的难点是多导弹网络的避障问题，该网络具有较高的目标捕获精度，以及有效协调各部件之间的碰撞时间［9］。

在目前文献中，针对多导弹网络提出了许多先进的协同制导策略。第一类方法研究对给定目标同时进行拦截的影响时间约束的设计。文献［7］中，在线性规划的基础上，提出了一种封闭形式的冲击时间控制制导律，它能使一组导弹在理想的时间内到达目标。然后利用时变导航增益来协调多导弹网络的冲击时间［10］。还提出了对时间约束制导的扩展以控制碰撞时间和碰撞角度［11］。上述制导策略通常要求每枚拦截导弹都能获得发射时间的全局信息。为此，提出了基于冲击时间约束的分布式控制体系结构，以增强多导弹协同工作能力［12］。使用离散拓扑模型调整特征期望的冲击时间［13］。

另一类方法采用leader-follower 模型来构建多导弹网络的协同制导模型。在文献［14-15］中，非线性状态跟踪控制器和状态调节器分别用于求解时间约束制导。然后将共识协议应用于leader-follower策略的设计，保证了每个follower 的影响时间在有限时间内收敛到leader。为了方便多导弹异质交战，提出了一种基于均衡导航（Proportional Navigation，PN）制导策略的分布式leader-follower 模型［16］。此外，利用虚拟leader 方案将约束制导问题转化为非线性跟踪问题来实现碰撞时间控制［17］。

影响时间约束和leader-follower 策略［18-20］促进了多导弹网络协调算法的发展，但在这些协同制导方法中，避障没有考虑在内。因此，本文提出了一种基于PN 的分布式制导算法的改进方法，以增强多导弹网络在避障条件下的交战能力。本文工作：1）基于PN 的制导策略以简单的形式开发，由目标捕获、时间协调和避障3 个独立组件组成；2）多导弹网络中的每个成员只需要邻居的出发时间信息就可以进行协同作战；3）在目标捕获精度较高的情况下，有效协调碰撞时间，实现了避障。

1 基本假设

在平面追击情况下简化弹靶的非线性问题，便于多导弹网络分布式协调算法的设计，本文假设一些常见的条件。

1）将拦截导弹和目标都视为平面上的几何点。

2）每枚拦截导弹的导引头和自动驾驶仪动力学比制导回路快得多。

3）各拦截导弹的速度是恒定的，加速度输入只改变其方向。

假设n 枚导弹参与多导弹网络，同时拦截静止目标。在特定假设下，多对一啮合的二维几何如图1所示。Mi表示各拦截导弹，T 表示目标，则追击情况：

图1 多对一交战的几何结构

本文研究是各导弹在不同初始条件情况下，寻找一种协调算法，在不发生障碍物碰撞的情况下，同时引导导弹群到达给定目标。

2 分布式协调算法

在传统PN 制导律的基础上，重点研究分布式布局下多节点网络的协调算法设计。提出协同制导策略由3 个独立的组成部分组成：

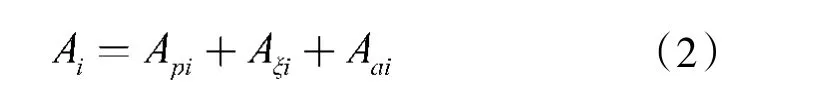
其中，术语Api、Aξi和Aai分别用于目标捕获、时间协调和避障。

PN 组件Api是由传统PN 制导策略在文献［3］得到：

如果ξi（t）→0 s 为ri（t）→0 km，则Aξi→0 m/s2为ri（t）→0 km。当导弹群接近给定目标时，作战时间的相对误差Aξi逐渐减小，协同分量的作用就会减弱。引导拦截导弹目标的同时，协调的设计变量tgo，i（t）将在接下来的部分讨论。

集中协调算法通常考虑多导弹网络中每个导弹与所有其他成员通信的情况。然而，当某些拦截导弹只能从其最近相邻导弹获取有效信息时，制导策略就失效了。因此，有必要选择协调变量tgo，i（t）对分布式时间的影响。图2 说明了多导弹网络中通信限制的示例。

如图2 所示，每枚导弹的有效通信区域用Si标记，Mi可以在该区域内获得其相邻导弹的出发时间信息。因此，这组导弹共有n 个通信区域，考虑这些通信区域的限制，协调变量tgo，i（t）中定义的组件Aξi分布形式：

图2 多导弹网络的通信限制

其中，si为区域Si内导弹总数。这也意味着Mi可以从分布通信区域内的si-1 邻居处获取多个时间信息。因此，组件Aξi调整同时到达的多导弹网络中每个成员的时间。然而，分布式设计并没有降低整个多网络的相对时间误差，而是降低了每个小群体的误差。通信区域的限制实际上是由通信系统的性能决定的。在目前的文献中，拦截导弹之间的距离通常用来表示通信限制。因此，本文也通过各导弹之间的相对距离来确定相邻导弹。

第3 个组件Aai是基于简单势函数设计的避障形式：

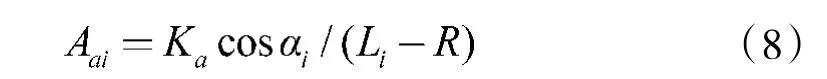
式中，Ka为增益参数，R 为障碍物的半径，Li表示障碍物和拦截导弹之间的距离。如图3 所示，此处使用圆形障碍物O，因为任何不规则形状的障碍物O1和O2都可以简单地替换。

图3 避障拦截导弹的几何结构

角度αi∈［-π/2，π/2］，i 是定义在视线框架相对于障碍的中心。可以发现，分量Aai主要取决于距离Li和航向角αi。具体来说，输入分量Aai的大小随着|Li - R|→0 km 和|αi|→0°的增加而逐渐增大，而较大的|Li- R|和|αi|则会导致加速度减小。

因此，基于这3 个组成部分，式（9）可以给出完整的多导弹网络分布式协调算法。目标捕获的效果由在整个参与过程中持续的PN 组件Api决定。当多导弹网络的发射时误差增大时，协调分量Aξi将决定式（9）制导算法。第3 部分Aai主要用于避障，在拦截导弹接近障碍物时生效。这3 个部分的集成产生一个权衡因子，以实现满足目标捕获精度和有效协调碰撞时间的避障。改进后的协调算法通过式（9）进行了简单的设计，因此，很容易实现。

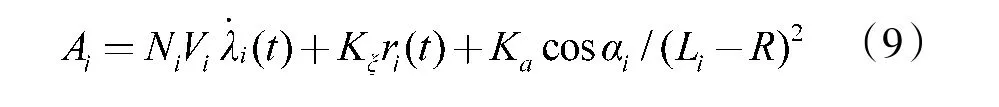
3 实验仿真

为验证所提分布式算法式（9），在同时到达的情况下进行了数值仿真，假设一组3 枚导弹参与多导弹网络，在不同初始条件下在（0，0）km 处拦截给定目标，如表1 所示。每个拦截器导弹极限加速度5.0×9.81 m/s2和导航常数3.0。设增益Ka为20，增益Aξ为30/（r0tgo0），其中，r0为初始导弹射程的平均值，tgo，0为初始到达时间估计的平均值。

表1 多导弹网络的初始条件

如图4 所示，多导弹网络选择了一种简单的通信拓扑，其中，M1和M3只能从相邻的M2获取发射时间信息。因此，3 导弹组的协调变量表示为

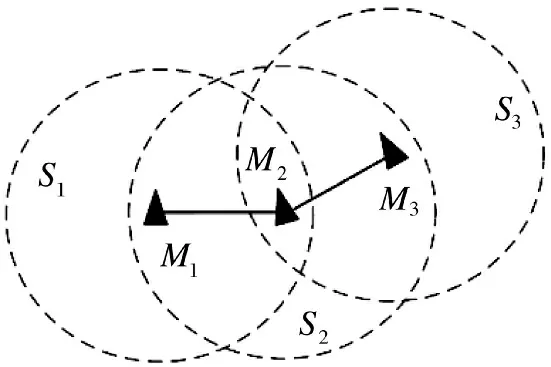
图4 多导弹网络的通信拓扑结构

其中，Si区域（i=1，2，3）导弹总数分别为s1=2，s2=3，s3=2。

图5 ～ 图6 给出了分布式协调算法的数值结果。Case 1 给出了没有分量Aai的简化制导策略的结果，协调算法式（9）的结果如Case 2。在Case 1 中，多导弹网络的地面航迹和时间表明，无Aai制导策略能在86.18 s 内驱动3 枚导弹同时拦截目标。但是，M3不能飞入给定（-14，5）、半径为2 km 障碍范围。相比之下，式（9）分布式协调算法成功地在0.1 s的色散范围内避障并同时到达。当冲击时间增加到94.13 s 时，这组导弹会移动更多的轮来避开给定的障碍物。

图5 拦截导弹对固定目标的地面轨迹

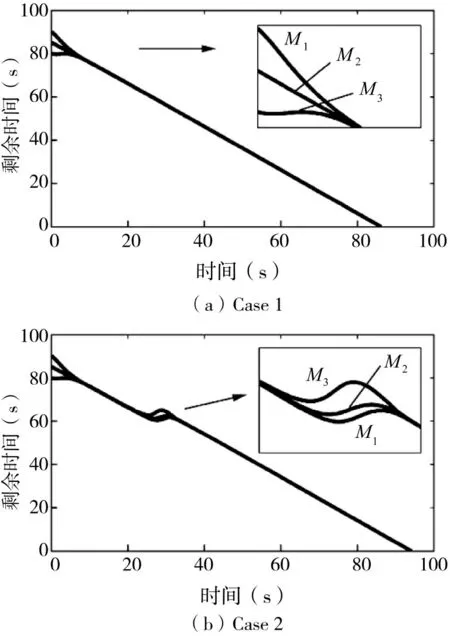
图6 拦截导弹对固定目标拦截的剩余时间

4 讨论

4.1 增益参数

关于协同制导策略式（9）的有效性，协调碰撞时间分量Aξi和避障分量Aai在很大程度上由增益参数Kξ和Ka决定。因此，适当选择这些增益变量可以保证多目标网络实现避障和同时到达。通过仿真验证了增益参数Kξ和Ka的影响。

首先，冲击时间的收敛速度主要受增益参数Kξ的影响。图7 为3 种拦截导弹的出发时间数值结果，其中，增益参数Kξ分别为20/（r0tgo，0）、30/（r0tgo，0）、40/（r0tgo，0）和50/（r0tgo，0）。很明显，当增益参数Kξ=50/（r0tgo，0）时，多导弹网络的出发时间具有最快的收敛速度。相反，当增益逐渐减小到Kξ=20/（r0tgo，0）时，速度变慢。仿真结果表明，当增益参数Kξ在20～50之间时，可获得较好的冲击时间协调性能。

图7 增益参数Kn 对剩余时间的影响

此外，通过另一个例子来检验增益参数Ka的影响。图8 给出了多导弹网络地面轨迹的数值结果，其中，增益Ka分别设置为10（波折号-点）、20（点）、30（波折号）和40（实线）。研究发现，当增益从Ka=10 增加到Ka=40 时，为了避开障碍物，这组导弹会越早越远。如图9 所示，当Aai组件选择较大增益Ka时，拦截导弹的控制性能（实线为M1，波折线M2，点为M3）要低得多。仿真结果表明，适当选取增益参数Ka在10～40 之间，能够较好地满足避障要求。

图8 增益参数Ka对地面轨迹的影响

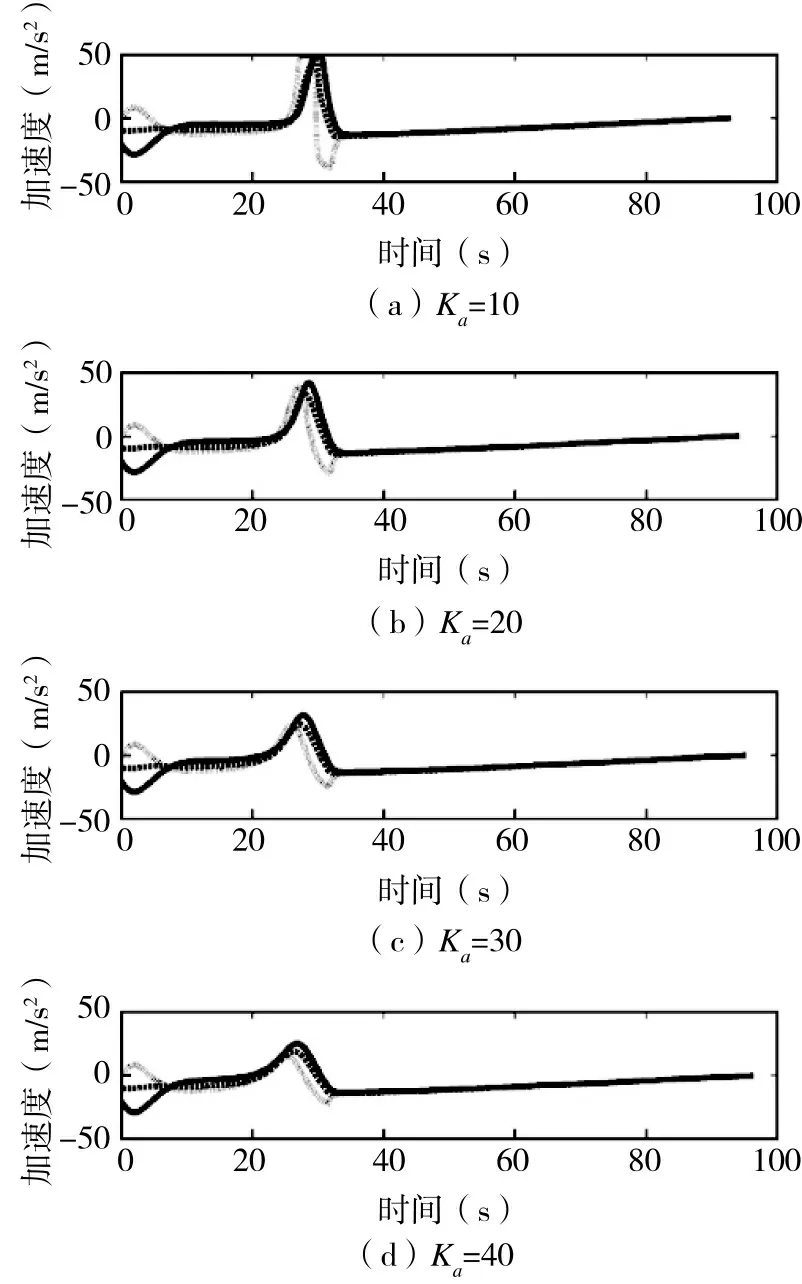
图9 增益参数Ka 对控制性能的影响

4.2 控制目标

选用一个机动目标协同作战的场景来验证所提出的协调算法。选择与上述相同的初始条件。设目标物体的速度和加速度为常数，即VT=100 m/s，AT=-2.0×9.81 m/s2。目标的初始航向角对惯性参考系将60°。

图10～图11 给出了对机动目标协同作战的仿真结果。用Case 3 和Case 4 分别展示了无组件Aai的协调算法和完整的协调算法式（9）。结果表明，多导弹网络中各成员对机动目标的拦截具有有效的碰撞时间协调。采用所提出的导引方法也可实现避障。由于在此场景中执行了头-追击制导，最终撞击时间逐渐增加。

图10 拦截导弹对激动目标的地面轨迹

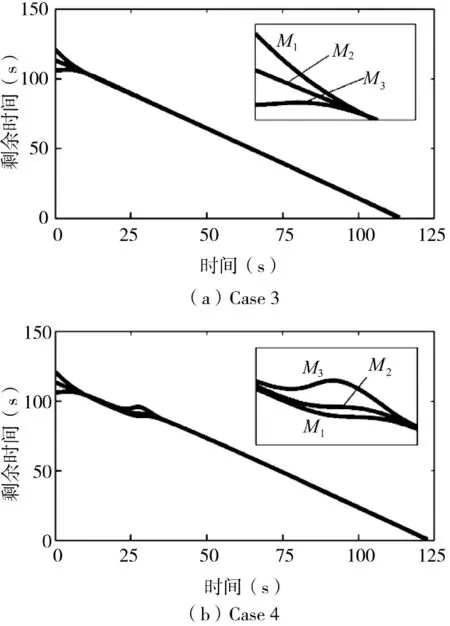
图11 拦截导弹拦截机动目标的剩余时间

4.3 障碍尺寸

针对协调算法中障碍物大小的影响，进行了数值仿真。协同作战场景下选择不同的障碍大小（R=2 km、3 km、4 km 和5 km），初始条件与上述相同。

图12 为拦截导弹的地面轨迹，实验结果表明，在障碍物大小达到5 km 的情况下，该制导策略仍能实现避障。碰撞时间协调有效，目标捕获精度较高。下页图13 说明了障碍物大小对加速度和移动时间的影响。可以发现，较大的障碍通常导致控制性能的早期饱和。随着障碍物尺寸的增大，多导弹网络的出发时间也随之增大。

图12 障碍物大小对地面轨迹的影响

图13 障碍物大小对加速度和剩余时间影响

5 结论

本文提出了一种分布式协调算法，该算法既考虑了避障问题，又考虑了拦截导弹之间的有限通信区域。

1）在传统PN 算法的基础上，提出了一种简单的引导策略。即使一些拦截导弹只能从最近的导弹收集信息，也能使同步到达成为可能。

2）仿真结果表明，适当选择增益参数Ka可以保证目标捕获精度和避障效果，冲击时间的收敛率由另一个结论决定。

3）分布式协调算法对于常见的障碍大小通常是有效的。该算法也可以实现对机动目标的协同拦截。