基于双谱切片小波包的雷达体制识别技术*
刘 傲,周 正,杨卫国
(1.海军航空大学,山东 烟台 264001;2.解放军91206 部队,山东 青岛 266109)
0 引言
电扫描天线可以通过微秒级的速度使天线波束指向产生捷变,使得相控阵雷达能同时对多个目标进行跟踪[1]。电子扫描体制雷达以其快速扫描能力、多波束形成能力、波束捷变能力等优势得到广泛应用[2],其与机械扫描雷达在脉冲宽度、脉冲重频、载频等参数使用上很相近[3-4]。目前,对不同体制雷达的区分主要集中于对脉冲幅度(PA)信息的提取上[5]。文献[6]通过脉冲幅度特性与正弦序列幅度特性的相似系数,来识别不同体制雷达;文献[7]根据侦察接收机信号强度的变化,结合天线方向图,建立信号幅度变化图,使用动态峰值搜索的方法找到峰值附近时间窗内相邻幅度差的均值变化规律,以此识别不同体制的雷达。
侦察接收机收到的信号中,含有热噪声、发射机噪声、杂波以及需识别的雷达信号。杂波及热噪声近似高斯分布,雷达发射机包含的噪声一般为非高斯的色噪声。而通过高阶谱分析的方法能够很好地抑制高斯色噪声,并使得信号幅度及相位信息得到较好保留[8]。高阶谱中,阶数和计算量最小的是双谱,并且尺度、时移不变性及相位保持性的特点,使得双谱分析在信号处理中更具有优势[9-11]。小波分析可以在时频域同时对信号进行处理,因此,可以区分出信号中的突变成分及噪声,完成信号去噪[12-13]。小波包是在小波分析的基础上,将高频部分进行正交分解。不同雷达的信号在通过小波包分解后重构系数会有区别,这些系数的能量也有较大差异,因此,小波包重构系数的能量特征常被用于信号的识别中[14-18]。
双谱分析虽然有尺度、时移不变性及相位保持性的特点,但双谱为三维特征,为降低运算量需进行降维处理;而小波包变换可使频带划分为多个层次,更好体现出不同信号的差异,从而弥补双谱分析的不足。本文提出了一种基于双谱切片小波包的雷达识别方法,首先将不同体制的雷达信号的脉冲幅度序列进行双谱分析,再将三维双谱特征进行切片处理,转换为二维特征,再进行小波包分解,通过支持向量机(Support Vector Machine,SVM)完成对不同体制雷达的识别。
1 ESM 截获雷达脉冲信号幅度序列
机械扫描雷达的扫描方式是通过伺服系统将天线的指向按一定的扫描周期连续改变。天线通过360°的旋转,使得ESM 截获的脉冲也呈现周期性。假设某机械扫描雷达的天线方向图函数呈高斯性,可表示为
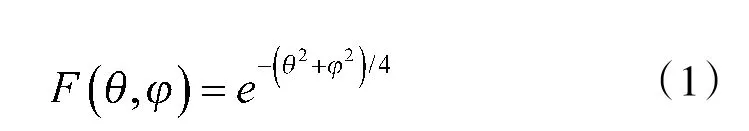
其中,θ 为方位角,φ 为俯仰角。
一维相控阵雷达通过线性相控阵天线,方位上为采用机械伺服机构带动的机械扫描方式,俯仰上为电扫描方式,方位、俯仰叠加后则是天线方向图[19-20]。
方位天线方向图函数为
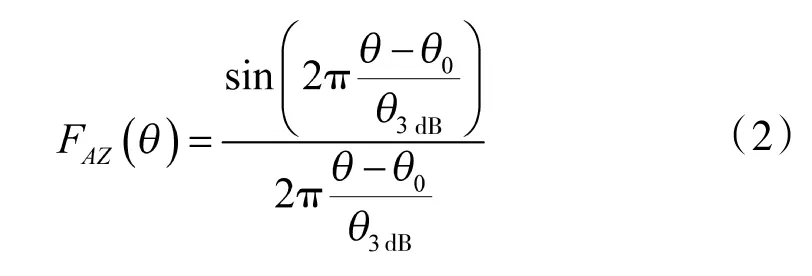
其中,θ 为方位角,θ0为最大指向角。
2 提取双谱切片小波包特征
2.1 信号的双谱
对雷达信号进行分析时,往往受到噪声的影响。双谱是对信号三阶积累量进行两次傅里叶变换,而通过高阶谱分析信号能有效降低高斯噪声的影响。所以,为抑制噪声,先对雷达信号提取双谱。信号双谱通过高阶积累量定义为:

双谱即三阶谱,其定义如下

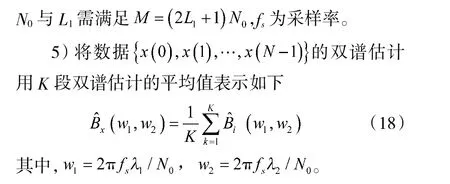
2.2 切片化处理
双谱为三维特征,若直接进行处理,运算量较大,所以需进行简化,提取其二维特征。简化时需遵循的原则有两个:一是减少运算量,确保算法的计算速度;二是简化后尽可能保证原有的特征。可沿X 轴作等间距截面,且此截面与YOZ 面平行,划分后得M 个部分,取其中双谱的最大值作为特征向量,即有新的二维特征Rx。这种直接切片取双谱幅度谱最大值的方法,避免了对分辨度不强的多余部分的计算,又能充分利用双谱三维特征的幅度信息,减少了计算量,得到较为有效的特征。

二维双谱特征可以反映出不同扫描方式间的不同,但这种二维特征不便于自动识别,需将其降维。
2.3 特征提取
小波包变换可以使频带划分为多个层次,更好体现出不同信号的差异,所以对二维双谱特征进行小波包分解处理。信号s(n)在不同尺度的小波包变换如下所示

具体流程如下所示:
1)小波基的选择通常依据支撑长度、对称性、正则性等标准。Symlets 小波系具备较好的正则性,在连续性、支撑长度、滤波器长度等方面与dbN 小波一致,但Symlets 小波具有更好的对称性,即一定程度上能够减少对信号进行分析和重构时的相位失真。本文选择Symlets 小波函数“sym6”和Shannon熵,对Rx采取L 层小波包分解的处理方式,分别从低到高频上第L 层的2L个特征。

3 识别步骤
本文所提出的基于双谱切片小波包特征的相控阵雷达体制识别步骤如下:
步骤1 对机械扫描雷达、一维相控阵雷达和二维相控阵雷达作双谱估计,其中包含对数据的归一化处理;
步骤2 沿双谱三维图的X 轴作等间距截面,且此截面与YOZ 面平行,划分后得M 个部分,取其中双谱的最大值作为特征向量,即为对3 种体制雷达双谱三维谱的切片处理,将特征转化为二维特征Rx;
步骤3 为便于识别,将切片后的二维图像通过小波包分解进行降维,对Rx采取L 层小波包分解的处理方式,分别从低到高频上第L 层的2L个特征,第L 层的2L个小波包系数进行重构,得出重构信号,并通过重构信号的能量构建归一化后的特征向量Wx。这里求二维特征Rx的3 层小波包分解,得到双谱切片小波包特征Wx。
步骤4 将Wx1作为特征参数通过SVM 对不同体制雷达进行识别。
4 仿真实验
4.1 不同雷达的双谱三维图
仿真实验时,ESM 在3 种体制雷达方向的(0°,10°)处,且假定各体制雷达互不干扰。ESM 每次可接收的波位数为6~10 个,每个波位上,雷达发射的脉冲数为20~100 个。3 种体制的雷达扫描范围在方位上为-60°~60°,俯仰上为0°~50°,周期为5 s,波束宽度为2°。其中,一维相控阵雷达俯仰方向天线阵元个数取值为30,二维相控阵雷达的平面相控阵天线为60×60,各阵元等间隔分布,方位和俯仰最大指向角分别为0°和10°。对3 种体制雷达信号取双谱三维图,每个信号分为10 段,每段256 个采样点,共取2 560 个采样点。图1~下页图3 分别是脉冲重复频率(PRF)为500 Hz、1 000 Hz、2 000 Hz 的256×256的双谱三维图,由图可见,不同体制雷达的双谱三维图区别较明显。

图1 500 Hz 3 种雷达双谱估计三维图

图2 1 000 Hz 3 种雷达双谱估计三维图
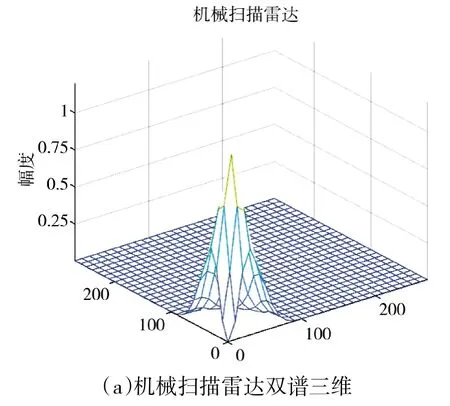
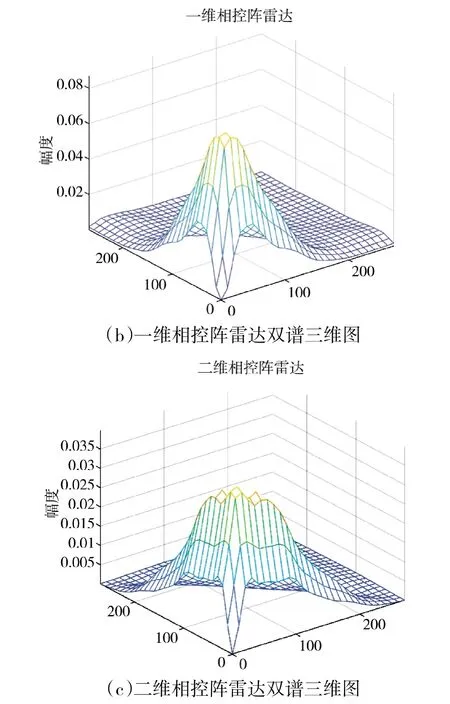
图3 2 000 Hz 3 种雷达双谱估计三维图
4.2 雷达脉冲的双谱二维切片图
将每个信号分为10 段,每段256 个采样点。图4~下页图6 分别是脉冲重复频率(PRF)为500 Hz、1 000 Hz、2 000 Hz 时,3 种雷达的双谱二维切片图。
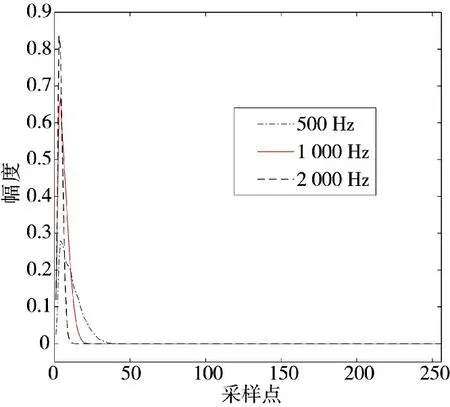
图4 机械扫描雷达双谱二维切片图
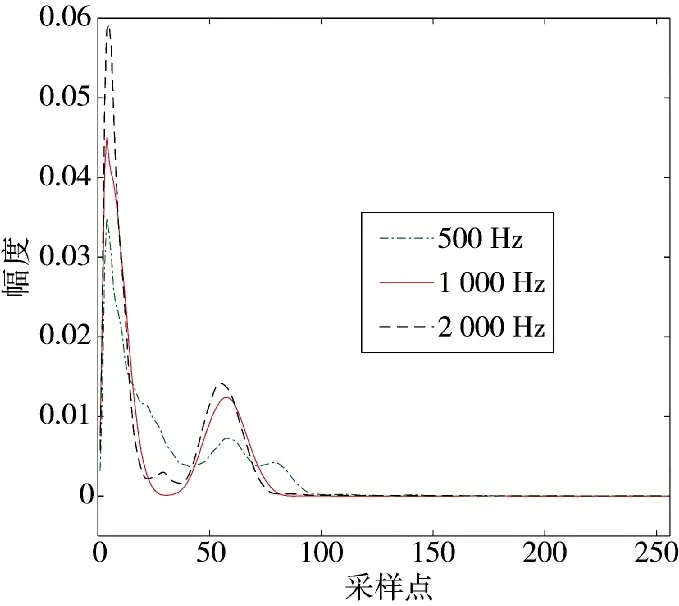
图5 一维相控阵雷达双谱二维切片图
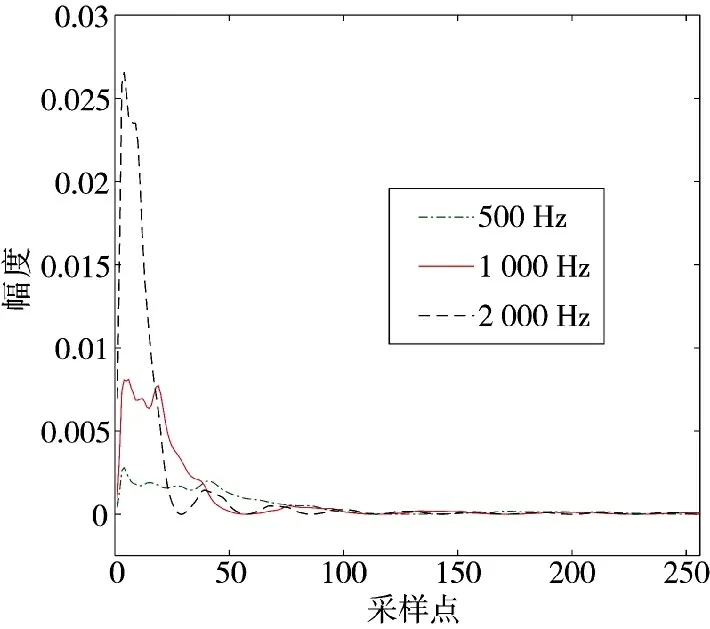
图6 二维相控阵雷达双谱二维切片图
图中各曲线幅度的最大值即为二维特征Rx取值,通过对比图中数值,可以看出3 种雷达在各PRF 上幅度的最大值Rx区别较为明显。
4.3 雷达体制的识别
仿真实验时,ESM 在3 种体制目标雷达方向的(0°,10°)处,且假定各体制雷达互不干扰。ESM 每次可接收的波位数为6~10 个,波位宽度与高度均为1°,每个波位上,雷达发射的脉冲数为20~100个。3 种体制的雷达扫描范围在方位上为-60°~60°,俯仰上为0°~50°,周期为2 s~5 s,波束宽度为1°~5°。其中,一维相控阵雷达俯仰方向天线阵元个数取值为30,二维相控阵雷达的平面相控阵天线为60×60,各阵元等间隔分布,方位和俯仰最大指向角分别为0°和10°。仿真参数均在参数区间上均匀分布。
1)特征提取
通过仿真,在PRF 分别为500 Hz、1 000 Hz 和2 000 Hz 的情况下,生成3 种体制雷达的双谱各50个,并提取Wx1,得到结果如下
从图7~ 图9 中可以看出,3 种不同体制雷达的双谱切片小波包特征存在较明显的区别,分离度较好。

图7 500 Hz 3 种雷达的Wx1 分布

图8 1 000 Hz 3 种雷达的Wx1 分布

图9 2 000 Hz 3 种雷达的Wx1 分布
实际测试中,往往伴随噪声等干扰因素,对信号脉幅的测量存在一定的误差,并且信号会因为淹没在噪声中而被过滤掉,存在丢失脉冲的情况。在模拟的信号中加入高斯噪声信号,取PRF 为500 Hz,将噪声占比设置为0~20%,在每种噪声下进行500 次蒙特卡洛实验,分别算出在不同脉冲丢失率下3 种体制雷达Wx1的均值,如图10~下页图12 所示。
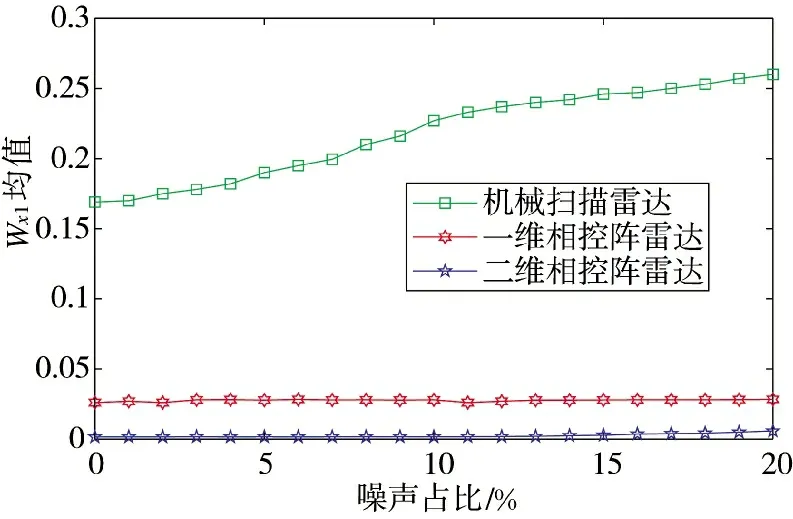
图10 Wx1 随噪声占比变化图,脉冲丢失率为5%

图11 Wx1 随噪声占比变化图,脉冲丢失率为10%
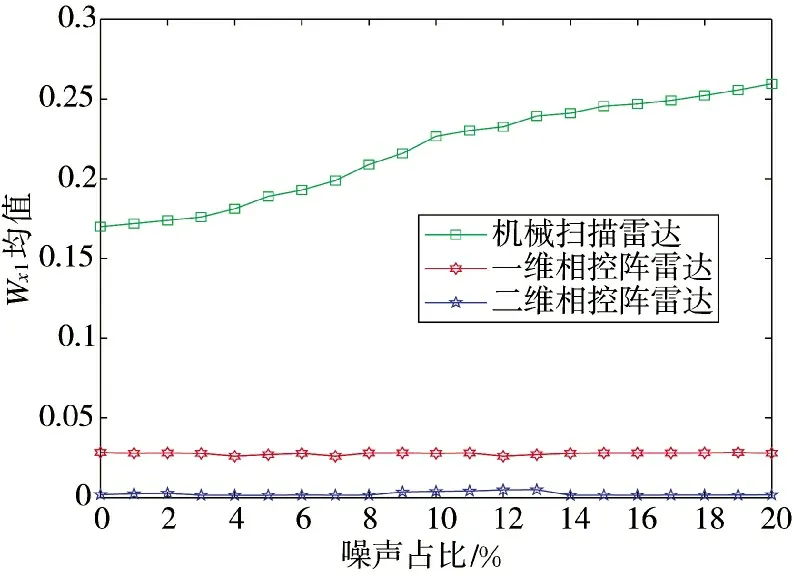
图12 Wx1 随噪声占比变化图,脉冲丢失率为15%
由图可知,噪声占比变化时,一维相控阵雷达的Wx1较为稳定,二维相控阵雷达的Wx1虽有增加趋势,但幅度不大。而机械扫描雷达的Wx1值随噪声占比的递增而增大,是因为噪声使得机械扫描雷达包络粗糙,频率分量有所增加。但总体来看,不同脉冲丢失率下3 种体制雷达Wx1较稳定,且识别率依然很好。
2)通过SVM 进行雷达识别
PRF 取1 000 Hz、2 000 Hz 时,分别加入高斯噪声信号,将噪声占比设置为0~20 %,在每种误差下分别进行500 次蒙特卡洛实验,分别算出3 种体制雷达Wx1的均值。对3 种PRF 下算出的3 000 组数据,通过SVM 进行识别,其中,SVM 核函数取径向基函数,核函数参数取1,惩罚系数取2。通过交叉验证法,把上述3 000 个数据平均分为30 组,每组100 个样本数据。每次仿真选取其中的5 组为训练集,另外25 组为测试集,交替循环30 次,就可使每组样本既为训练集,又为测试集。得到30 次实验结果的平均值为正确识别率,如图13 所示。

图13 噪声占比变化对正确识别率的影响
由图可知,相对噪声占比变化时,正确识别率仍能达到93%以上,说明以双谱切片小波包作为识别特征效果较好。
3)方法对比
文献[24]提出了频谱边带小波包特征用于识别雷达辐射源。为一步验证本文方法的性能,将文献[24]方法的正确识别率同本文进行对比,仿真条件同上文,并计算使用两种特征所耗平均时间,结果如图14 和表1 所示。

图14 两种方法识别率对比

表1 两种特征的平均识别时间
综上所述,在相同噪声占比下,本文方法识别准确率较高,且识别时间短。这是因为双谱分析有效抑制了高斯色噪声对雷达信号的影响,保留了信号幅度及相位信息,也使得处理计算量变小,缩短了运行时间。
5 结论
本文通过对不同体制雷达信号的脉冲幅度序列进行双谱切片分析和小波包分解,提出双谱切片小波包这一识别特征,并用SVM 进行识别。经过仿真,证明该特征能够很好地识别不同体制雷达,并且在0~20%的噪声占比下,仍具有较好识别率,且耗时较少,具有一定的参考价值。

