台风作用下风-浪-潮三维环境等值面模型

魏 凯，钟 茜，沈忠辉，秦顺全,2

(1. 西南交通大学土木工程学院桥梁工程系，成都 610031；2. 中铁大桥勘测设计院有限公司，武汉 430034)

台风是我国东南沿海常见的灾害性天气[1]，登陆时常伴随着强风、巨浪、风暴潮，给近海工程，特别是跨海大桥的设计、建造和安全运营带来了严峻挑战[2]。近年来，桥梁风致振动[3-7]、波浪对桥梁的动力作用[8-11]、风-浪作用下的桥梁动力响应得到了较多关注[12-13]。风暴潮作为台风造成的海面异常升高现象，会加剧波浪对桥梁基础等结构的冲击作用[14]。随着跨海大桥跨径增大，风-浪-风暴潮增水(以下简称“潮”)共同作用下桥梁结构动力响应愈发明显，如何获取台风下的风、浪、潮数据并且确定给定重现期下的荷载参数成为制约跨海桥梁设计的关键科学问题。

我国过去在确定给定重现期下桥梁的风、浪、潮荷载参数时，常忽略变量间的相关性[2]。然而，台风下的风、浪、潮参数并非相互独立。现场实测是获取长期风、浪、潮数据以开展后续研究的有效途径，但由于布点有限、数据保密以及仪器损坏等原因，获取台风下的风、浪、潮数据非常困难。常根据有限的资料计算给定重现期下环境变量，陈子煜等[15]使用1984 年-2005 年间中国南海海域的观测资料推测了100 年一遇的风暴增水和波高。近年来，随着数值模拟技术的快速发展，台风作用下海洋环境参数数值模拟得到了广泛应用。Chen 等[16]基于FVCOM 耦合模型模拟了中国沿海9 个站点35 年波高与风暴潮参数，并将其用于计算联合概率密度。魏凯等[17]则利用SWAN+ADCIRC 开展了台风下近岸海域波浪-风暴潮耦合数值模拟，并通过实测数据验证了方法的有效性。

获取台风期间风、浪、潮数据之后，下一步就是如何考虑三者的相关性并确定不同重现期下的环境荷载参数。API RP 2A-WSD 设计规范[18]和DNV-OS-J101 设计规范[19]指出，在建立多个随机环境参数与重现期的关系时，可先建立多维联合概率分布，然后构造环境等值面模型。Copula 函数可将多个一维边缘分布连接起来，描述多变量间相关结构[20]，近年来被广泛应用于海洋环境下的多参数联合概率分析。环境等值面是由环境变量构成的面，可根据概率分布由一阶逆可靠度理论(IFORM)得到，其提供了给定重现期下多个环境荷载参数的组合[21]。上述研究为构建台风作用下的风-浪-潮三维联合概率和环境等值面模型提供了重要思路。

因此，本文以在建的西堠门公铁两用大桥所处的舟山海域为例，采用SWAN+ADCIRC 建立台风作用下海洋环境参数数值模型，通过对1987 年-2018 年49 条历史台风下的风、浪、潮进行数值模拟，获得台风下的风、浪、潮数据；采用嵌套Copula函数拟合上述数据，构造风-浪-潮三维联合概率分布；根据IFORM 建立并得到了100 年重现期下的环境等值面；重点讨论了4 种环境参数选取方法对环境等值面模型的影响。

1 台风下风-浪-潮参数数值模拟

1.1 台风风场模型

本文的台风风场模型由参数风场(包含移行风场和梯度风场)及背景风场叠加组合而成。其中，移行风场采用宫崎正卫模型[22]，移行风速vm根据台风中心的位置变化进行计算，其表达式为：

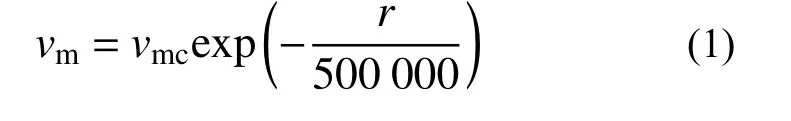
式中：vmc为台风中心移行风速；r为计算点到台风中心的距离。

梯度风场采用Holland 气压模型[23]，梯度风速vg通过求解环流空气质点的离心力、科氏力和压力梯度力构成的梯度方程得到(忽略地面摩擦力的影响)，其表达式为：

式中：P0为台风中心气压；ρa为空气密度；ΔP为外围气压(取1010 hPa)与中心气压P0之差。

梯度风vg通过0.9 的高度系数从大气边界层转换到海面高度[25]，海面高度处的梯度风vgs与根据台风中心位置变化计算得到的海面高度处的移行风矢量叠加合成经验台风场ve，如式(5)。

背景风场较参数风场能更精确地模拟距台风中心较远的风场，可利用其对参数风场进行改善[26]。本文选用Cross-Calibrated Multi-Platform(CCMP)再分析数据库提供的全球尺度的背景风场与上述参数风场按照距离加权叠加，如式(6)[27]，得到改进的台风风场。在台风中心处为经验台风场，离台风中心较远处为CCMP 背景风，过渡区为经验台风场ve与CCMP 背景风vb的结合，通过与到台风中心处距离相关的系数α 进行叠加，α 的计算公式如式(7)。

式中：R1取300 km；R2取400 km。

1.2 边界水位模型

边界水位采用TPXO9_atlas 模式中8 个主要分潮(M2、S2、N2、K2、K1、O1、P1、Q1)进行模拟。

1.3 台风下波浪-风暴潮耦合模拟方法

台风作用下波浪-风暴潮的模拟利用SWAN+ADCIRC 耦合模式进行。SWAN 基于波作用量守恒方程进行计算，其考虑了风能输入，白帽耗散、底部摩擦，深度诱导破碎及非线性波-波相互作用等物理过程[2]。ADCIRC 模式基于广义波动连续性方程和动量方程求解流速、水位。SWAN 与ADCIRC 共用一套网格，在台风风场和边界水位的共同驱动下，ADCIRC 将计算出的流速、水位传递给SWAN，SWAN 再将其计算出的波浪辐射应力传递给ADCIRC 以实现耦合[25]，如图1 所示。风速(Vw)、有效波高(Hs)可由耦合模式直接输出，风暴潮(S)可利用数值模拟出的水位减去天文潮获得。其中，天文潮位利用无风场输入、仅由边界水位驱动的ADCIRC 模式进行模拟，这里的边界水位同样由TPXO9_atlas 模式进行计算。上述数值模拟方法的有效性已在作者之前的研究[25]中进行过验证。

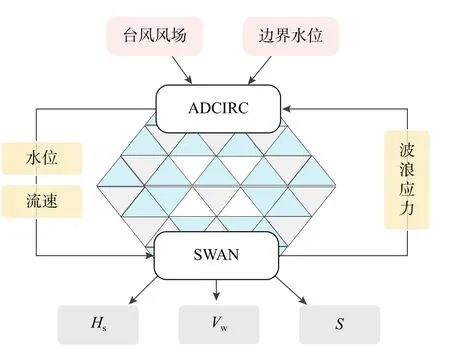
图1 SWAN+ADCIRC 耦合模型Fig. 1 SWAN+ADCIRC coupling model

2 数值模型验证及风、浪、潮选取

2.1 算例海域数值模型

常年受台风影响的舟山海域位于浙江省东北部，该地区周边经济发达，人口稠密，海域内建有多座跨海大桥。以舟山西堠门公铁两用大桥所在海域为中心，建立范围大致为115°E～127°E，25°N～41°N(网格边界为曲线，非矩形)，包含了渤海、黄海以及东海部分海域的数值模型，如图2所示。工程海域附近网格尺寸最小为150 m，外海最大网格尺寸约60 km。采用非结构化三角形网格，网格数为70144，节点数为37064。

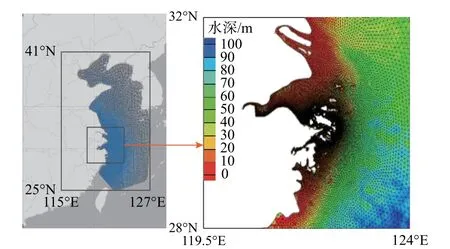
图2 计算域网格及舟山海域水深Fig. 2 Model domain with unstructured triangular grids

2.2 数值模型验证

合成风场的准确性通过对9711 号台风“温妮”及1509 号台风“灿鸿”期间的风速模拟进行验证。台风“温妮”路径如图3 中带矩形标记的线所示。利用合成风场模拟了1997 年8 月17 日0 时-1997 年8 月20 日0 时的风场，以定海站的实测风速[28]进行对比验证，如图4(a)所示。台风“灿鸿”路径如图3 中带圆形标记的线所示。同时利用合成风场模拟了2015 年7 月8 日12 时-2015 年7 月12 日0 时的风场，以南麂岛站实测风速[29]进行对比验证，如图4(b)所示。合成风场对台风期间的风速变化趋势及极值均吻合较好。

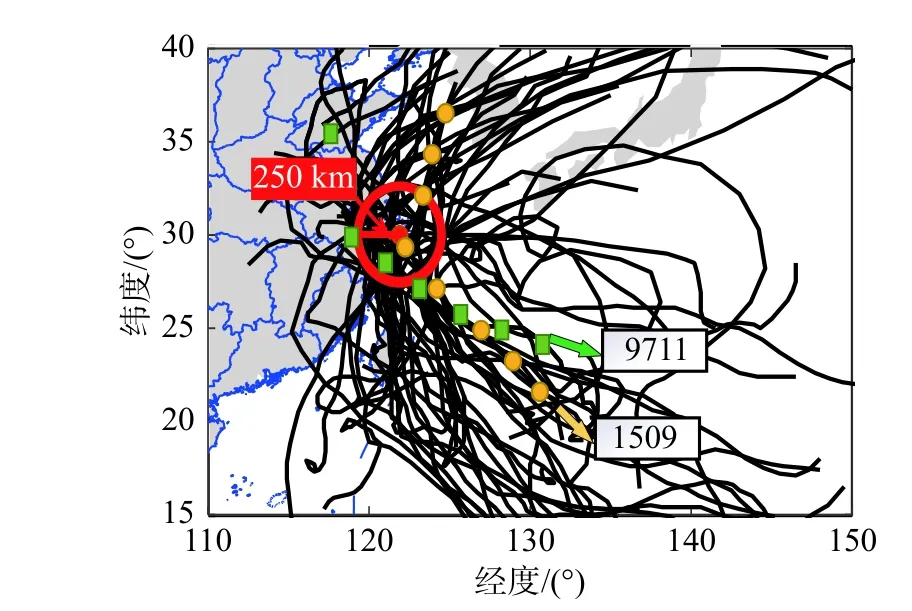
图3 所选计算台风路径Fig. 3 Traces of selected tropical cyclones

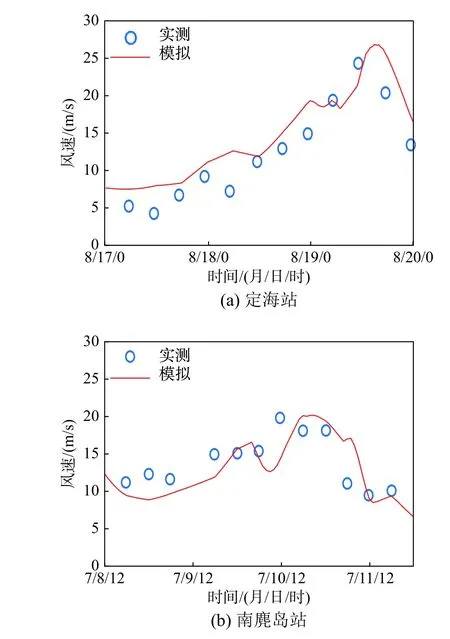
图4 实测风速与合成风速比较图Fig. 4 Comparison of calculated and measured wind speeds

为验证数值模型模拟波高的有效性，模拟了1997 年8 月17 日0 时-1997 年8 月20 日0 时9711号台风“温妮”期间的环境参数。以镇海站的实测波高[28]进行对比验证，如图5(a)所示，实测最大波高为2.97 m，模拟最大波高为2.98 m，相对误差为0.3%。还模拟了2015 年7 月9 日12 时-2015 年7 月11 日12 时1509 号台风“灿鸿”。图5(b)给出了在南麂岛测站的数值模拟与实测有效波高[29]的对比图。由图5(b)知，实测最大有效波高为5.69 m，模拟最大有效波高为5.74 m，相对误差为0.9%。数值模拟具有较高精度。

图5 有效波高实测值与模拟值对比Fig. 5 Comparison of calculated and measured significant wave heights

为验证数值模型模拟风暴潮的有效性，同样利用台风“温妮”期间定海站的实测风暴潮增水[28]进行对比验证，如图6(a)所示，实测最大增水为1.44 m，模拟最大增水为1.17 m。还模拟了2012年8 月6 日0 时-2012 年8 月9 日0 时1211 号台风“海葵”期间的环境参数。以“MJ”站的实测风暴增水[24]进行对比验证，如图6(b)所示，实测最大增水为1.31 m，模拟最大增水为1.58 m。数值模拟增水与实测增水吻合良好。

2.3 台风作用下风、浪、潮参数选取

仅关注某区域的环境变量时，为了节约计算资源，常忽略强度较低、距离较远的台风，只对经过指定范围的台风进行研究。Li 和Hong[30]选择200 km、250 km、300 km 作为台风的选取半径，以研究台风选择范围对估计诱发灾害的影响，结果表明三种情况相差很小。基于验证的数值模型，根据中国台风网历史台风库数据，选取1987 年-2018 共32 年间，对途经以金塘水道中点为圆心、250 km 为半径范围内的49 条台风(如图6 所示)进行数值模拟，获得了各台风过程中风速Vw、波高Hs、风暴潮增水S的时程数据。这里的风速Vw指的是海平面以上10 m 高度处10 min 平均风速；波高Hs指的是有效波高；风暴潮S指的是台风引起的风暴潮增水。这里的风、浪、潮数据利用第1.3 节中描述的方法获取。

图6 风暴增水实测值与模拟值对比Fig. 6 Comparison of calculated and measured storm surges

需要注意的是，一次台风过程中的风、浪、潮往往不会同时达到最大，风、浪、潮参数选取会影响后续联合概率分析的结果。刘德辅等[31]指出，当结构最敏感荷载类型不明确时，可分别取不同时刻环境参数构建复合极值分布。因此，本文分别以风、浪、潮最大时刻以及假设三者同时取最大这四种情况选取每个台风的风、浪、潮参数，根据49 个台风的选取结果建立四个数据集，如表1 所示。4 个数据集中风、浪、潮数据均值与标准差如表2。

表1 4 个数据集风、浪、潮的选取方式Table 1 Four ways of selecting wind, wave and storm surge data

表2 4 个数据集中环境参数均值与标准差Table 2 Means and standard deviations of environmental parameters of four data sets

数据集一的最大风、浪、潮分别为31.48 m/s、5.02 m、1.17 m；数据集二的最大风、浪，潮分别为31.49 m/s、4.97 m、1.86 m；数据集三的最大风、浪，潮分别为31.00 m/s、3.36 m、1.86 m。这三个数据集49 条台风过程中的最大风速基本一致，最大波高数据集三较小，最大风暴潮数据集一较小。数据集一、数据集三与数据集四风速差值的方差分别为1.4 m/s、4.5 m/s；数据集一、数据集二与数据集四的风暴潮差值的方差分别为0.38 m、0.33 m；数据集二、数据集三与数据集四的波高差值的方差分别为0.38 m、0.77 m。数据集三反映的每条台风期间风、浪的值偏小。

3 风-浪-潮参数联合概率Copula 模型

3.1 多维联合概率模型

Copula 函数可用于多维联合概率的建立。由Sklar 定理，对于具有一元边缘分布函数F1,F2, ···,Fn的联合分布函数F，一定存在Copula 函数C，满 足 式(8)[2]，若 边 缘 分 布 函 数F1,F2, ···,Fn连续，则C唯一确定。采用嵌套Copula 函数建立风-浪-潮联合概率分布，如式(9)。

3.2 风、浪、潮参数边缘分布

采用广义极值分布(GEV)对风速、波高、风暴潮的边缘分布进行拟合，GEV 表达式如下：

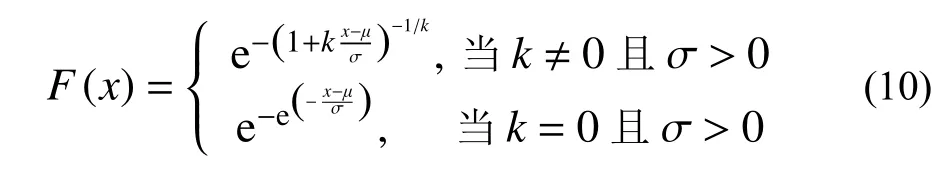
式中，μ、σ、k分别为位置参数、尺度参数、形状参数。

利用最大似然法拟合边缘分布相关参数，并用RMSE 及5%显著水平的K-S 检验进行拟合程度判断。其中RMSE 计算如下：

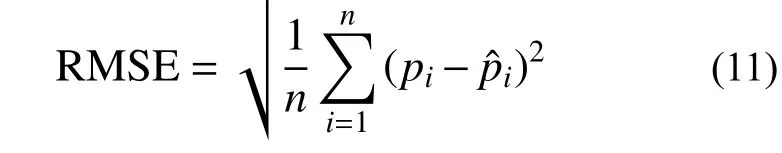
式中：n为观测值个数；pi为根据数据直接计算出的经验频率；pˆi为按照拟合的边缘分布得出的理论频率。

四个数据集边缘分布拟合参数及检验结果如表3。利用GEV 能较好拟合风、浪、潮的边缘分布。

表3 广义极值分布参数Table 3 Fitted parameters of GEV

3.3 风-浪-潮三维联合概率分布

获得边缘分布后用Copula 函数将两个边缘分布连接起来。选取水文分析中常用的Frank Copula拟合风-浪、浪-潮、风-潮三个组合的二维联合分布，拟合结果如表4 所示，其联合概率分布表达式如式(12)。

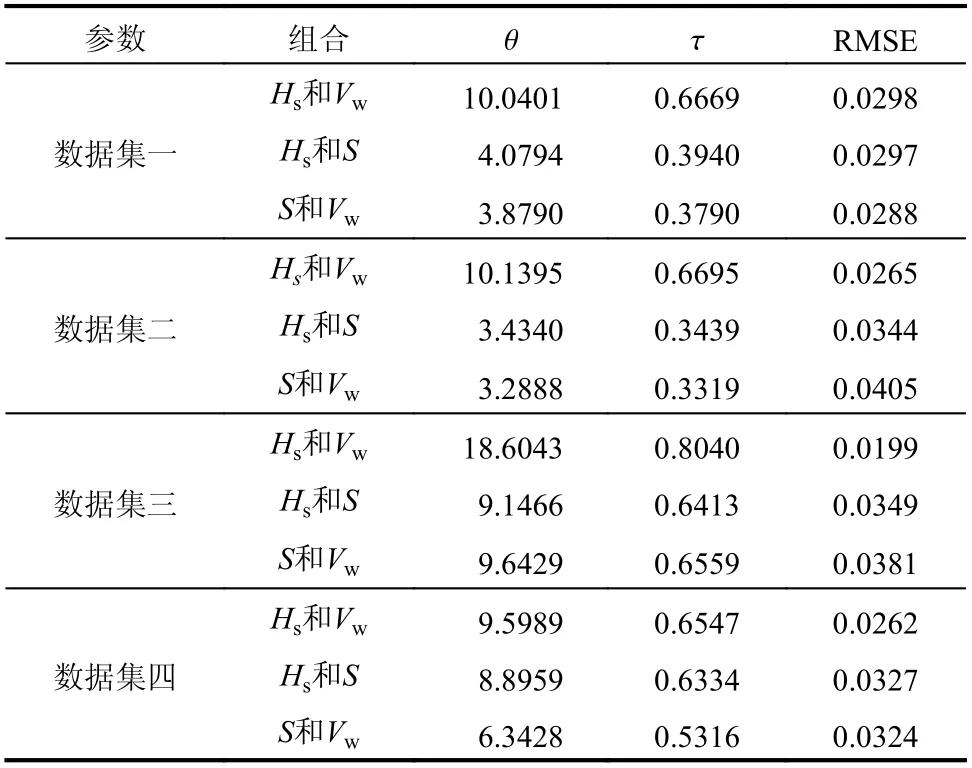
表4 二维Frank Copula 联合分布相关参数Table 4 Fitted parameters of Frank Copula

1) Frank Copula：

联合分布函数和概率密度函数的关系为：

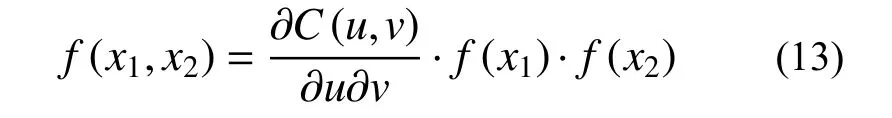
式中：f(x1,x2)为二维联合概率密度；f(·)为概率密度函数。

利用Frank Copula 函数拟合后以RMSE 进行评判，由表4 可知，Frank Copula 函数对三个组合的联合分布拟合优度均较好，其能反映各变量间的相关性，故三维Copula 的第一层函数选择Frank Copula。

三维Copula 的第二层函数一般取相关性较强的组合[2]。Kendall 相关系数τ 可利用Frank Copula函数中的θ 相关性系数进行估计，如式(14)[32]，利用其计算得到“波高和风速”、“波高和潮位”、“潮位和风速”的τ 如表4。τ 越大变量间相关性越强，由表3 可知，三种二维变量组合中风-浪相关性最强，且拟合程度较好，故将风-浪联合分布作为三维Copula 的第二层函数。综上，风-浪-潮联合概率构建过程如图7 所示，其概率分布及概率密度表达式如式(15)～式(16)。

图7 构建风-浪-潮联合分布Fig. 7 Construction of wind-wave-tide joint distribution

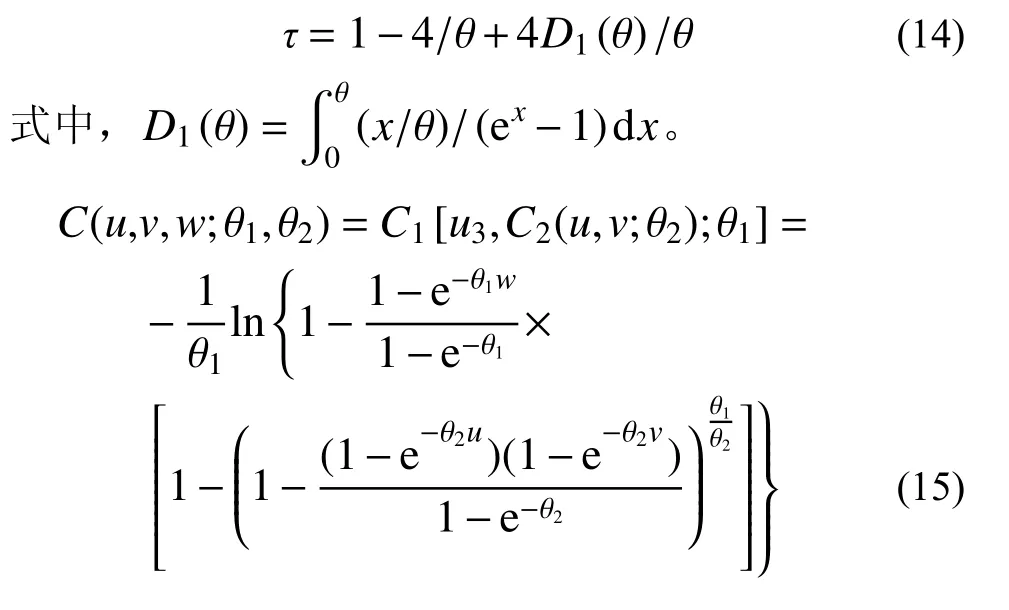
式中：f(x1,x2,x3)为三维联合概率密度；w为变量X3的边缘分布函数。

RMSE 值越小，说明函数拟合越好，4 个数据集风-浪-潮联合分布RMSE 分别为0.0313、0.0438、0.0381、0.0363，三维嵌套Frank Copula 能较好拟合4 个数据集的风-浪-潮三维联合概率分布。

4 风-浪-潮三维环境等值面模型

4.1 环境等值面模型的确定方法

给定重现期的风-浪-潮参数可以通过联合超越概率或IFORM 确定。后者能提供给定重现期下的环境等值面，为分析结构响应带来便利。基于Rosenblatt 变换的IFORM 可将三个不相关标准正态分布变量U1、U2、U3构造的半径为γ 的球面转换到由风、浪、潮构成的联合随机变量空间[33]。球面半径γ 与重现期T及随机事件平均年发生次数N(本文为1.53)的关系如下：

4.2 环境参数选取对环境等值面模型的影响

基于四个数据集，根据上述方法构建了舟山海域100 年重现期下的环境等值面，对比图8 中4 种数据选取方法构造的环境等值面：a)在波高方向上取值较大，形状较扁平；b)在风速方向上取值较大；c)在风暴潮增水方向上取值较大，在风、浪、潮处在较低水平时，环境等值面出现“尖角”；d)在风、浪、潮处于较高水平时较a)、b)、c)更加“饱满”。风-浪-潮环境等值面形状受数据选取方式影响较大。

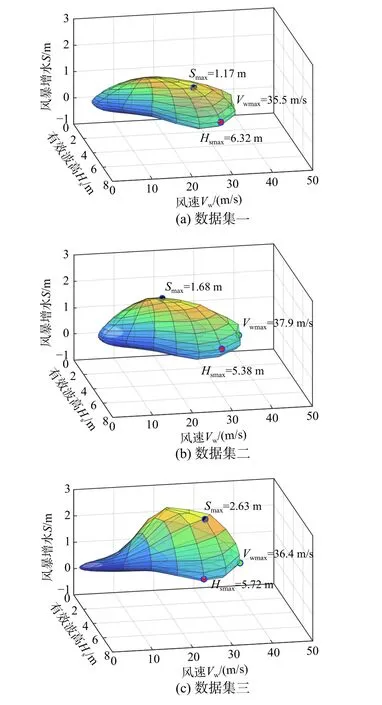
图8 基于不同数据集构造环境等值面Fig. 8 Environmental contours with 100-year return period constructed with data set

4 个环境等值面的最大波高、风速、潮位见表5。数据集一、数据集二、数据集三求到的最大波高与数据集四的相对差异分别为0%、17%、14%；最大风速与数据集四的相对差异分别为6%、0%、4%；最大风暴潮与数据集四的相对差异分别为56%、36%、0%。风暴潮最大值受参数选取时刻影响最大。若结构响应对风暴潮较敏感，而选取风、浪最大时刻参数构建环境等值面模型可能导致结构不安全。

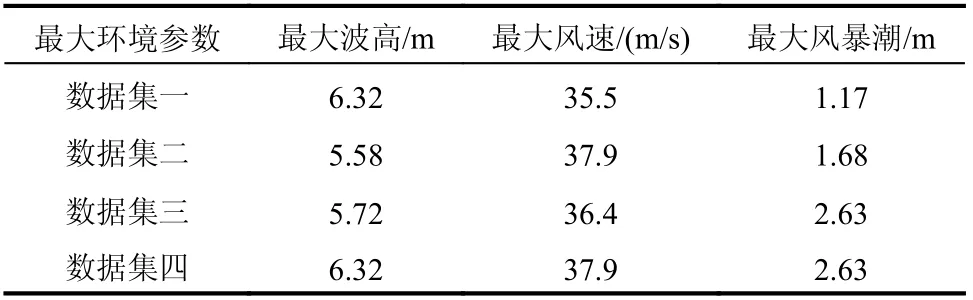
表5 100 年重现期下4 个数据集的最大环境参数Table 5 Maximum environmental parameters with 100-year return period constructed by four data sets

不考虑变量间相关性，利用边缘分布计算得到100 年重现期的浪、风、潮值分别为6.57 m、38 m/s、2.64 m，其直接组合结果如图8(d)中“+”点所示。该点位于100 年环境等值面外，重现期大于100 年，说明不考虑相关性直接组合估计的方式偏保守。

5 结论

利用SWAN+ADCIRC 耦合模式对32 年间影响舟山海域的49 次台风进行模拟，建立了4 个风、浪、潮数据集。在拟合边缘分布和二维联合分布的基础上利用嵌套Frank Copula 函数建立风-浪-潮三维联合概率分布，并利用IFORM 方法计算了100 年重现期下风-浪-潮的环境等值面。主要结论如下：

(1) 本文建立的数值模型能较好地模拟台风作用下舟山海域风、浪、潮环境的发展历程，为后期构建联合概率分布模型及环境等值面模型提供了可靠的数据来源。

(2) 用GEV 拟合台风期间风、浪、潮的边缘分布，Frank Copula 拟合风-浪、风-潮、浪-潮的二维联合分布，由此建立的三维嵌套Frank Copula能较好反映4 个数据集的风-浪-潮特征。

(3) 舟山海域给定重现期的环境等值面形状受数据选取时刻影响较大，其中风暴潮增水对选取方法最为敏感。不考虑风、浪、潮相关性，会高估给定重现期下的参数。

本文研究了基于台风数值模拟构建风-浪-潮联合概率及环境等值面模型的方法。碍于篇幅，本文未能结合实际工程，给出波-潮等作用的最不利叠加方法。未来应利用环境等值面上风-浪-潮变量的不同组合，从工程角度出发，分析结构受力和响应，通过研究结构响应与环境变量间的关系，为不同结构风、浪、潮设计参数的组合方法提供理论依据。