基于深度学习的RC 梁集中塑性铰模型参数研究

韩小雷，冯润平，季 静，吴梓楠

(1. 华南理工大学土木与交通学院，广州 510640；2. 华南理工大学亚热带建筑科学国家重点实验室，广州 510640)

建立能够准确反映构件的力学性能的结构计算分析模型对抗震设计至关重要，有学者基于试验数据对RC 梁在往复荷载作用下的受力特点与极限变形能力进行研究[1-2]。且目前国内外已形成较为完善的基于宏观单元的钢筋混凝土结构弹塑性分析方法[3]，其中梁柱构件常采用分布塑性铰模型或集中塑性铰模型进行模拟。

纤维模型是常用的分布塑性铰模型，存在应变局部化问题[4]，需通过调整纤维材料的软化斜率或端部积分点的权重[5]来规避，导致分析结果缺乏客观性，且计算耗时长。集中塑性铰模型不存在前述问题，计算量小，收敛性易于保证，但需通过试验数据从构件层次进行本构参数标定。

目前常用的集中塑性铰模型包括理想弹塑性双线型模型、BWBN(Bouc-Wen-BaberNoori)模型[6]及修正的IMK(Ibarra-Medina-Krawinkler)模型[7]等。国内外众多学者基于试验数据库对集中塑性铰模型本构参数进行公式回归[8-14]。Yu 等[8]基于30个剪切破坏的钢筋混凝土柱构件对捏拢型BMBN模型控制参数进行回归分析；Haselton 等[9]基于255 个弯曲破坏的钢筋混凝土柱试验数据，回归得出钢筋混凝土柱IMK 模型参数经验公式；Seok等[10]基于40 个剪切破坏的钢筋混凝土柱子，采用多元回归分析提出了IMK 模型参数的经验公式；Lignos 等[11-12]基于200 个钢筋混凝土梁试验数据进行IMK 模型骨架参数的校准，并基于151 个钢柱试验数据采用多元回归提出钢柱IMK模型骨架参数；Dai 等[13]基于103 根锈蚀RC 方柱构件试验数据，采用逐步回归分析建立IMK 模型参数经验公式，并基于76 根RC 圆柱实验数据，采用多元线性回归和分布拟合提出了IMK 模型参数经验预测公式[14]。

集中塑性铰模型参数与构件试验参数间存在复杂的联系，拟合的经验公式缺乏充足的泛化能力，而具备强大非线性数据分析能力的智能算法如神经网络能有效地解决这一问题。近年来已有学者逐渐将神经网络应用到土木工程研究当中，姜亚丽等[15]采用神经网络预测桥梁结构在地震下的结构响应；Ning 等[16]基于251 根RC 柱试验数据，采用神经网络模型对BWBN 模型参数进行预测；Naderpour 等[17]基于PEER 试验数据库采用神经网络算法预测钢筋混凝土构件的变形及承载能力。

本文基于试验结果对Pinch-IMK 模型本构骨架参数和滞回参数进行辨识，得到182 组骨架参数数据和91 组滞回参数数据，以构件特征参数为输入，以三折线骨架特征点参数、滞回参数为输出，建立Pinch-IMK 集中塑性铰RC 梁构件参数深度学习预测模型(HDLM)。将HDLM 预测骨架特征点参数与截面分析及现有经验公式等方法的计算结果作对比；将基于HDLM 预测参数计算的滞回曲线与基于经验公式的IMK 模型计算结果进行对比。

1 Pinch-IMK 模型介绍

Lignos 等[7]提出了修正的IMK 恢复力模型理论。Pinch-IMK 模型的骨架曲线正、负不同性，如图1 所示，除弹性刚度K外，各向包含6 个骨架参数，分别为硬化系数αs、屈服强度My、残余强度系数R、强度峰值点塑性变形θp、残余强度点塑性变形增量θpc和极限转角θu。

图1 Pinch-IMK 骨架参数Fig. 1 Pinch-IMK skeleton parameters

如表1 所示，Pinch-IMK 包含12 个滞回参数，可分为10 个退化参数及2 个捏拢参数，分别为基本强度退化参数λS及其退化指数CS、峰值强度退化参数λC及退化指数CC、再加载强度退化参数λA及退化指数CA、卸载刚度退化系数λK及退化指数CK、正负退化速率D、捏拢参数Fpr及Ap。

表1 Pinch-IMK 模型参数Table 1 Pinch-IMK model parameters

如图2 所示，通过调整骨架参数可表征试验构件的延性及承载力，通过调整滞回参数不仅可表征延性构件饱满的滞回环特性，亦可表征脆性构件的捏拢效应。通过改变模型的关键参数，可以有效地模拟RC 梁不同破坏形态下的滞回特性，如强度退化，刚度退化及捏拢效应。

图2 模型模拟构件滞回特性Fig. 2 The model simulates the hysteretic characteristics of components

2 RC 梁试验数据库

收集国内外共91 根RC 梁的低周往复试验数据并建立数据库。数据库包含两部分内容：

1)基本信息：梁的破坏形态、加载方式、试验材料强度信息、梁的几何信息及梁的配筋信息；

2)试验结果：基于文献中试验测量结果得到的滞回曲线和骨架曲线。

为得到更准确的拟合结果，防止深度神经网络由于过拟合导致泛化能力不足，所收集试验数据的各特征参数范围应尽可能的宽广，但仍需控制在工程设计应用中常见的范围内。所有试件的主要特征参数统计结果如表2 所示，所收集RC 梁构件的控制参数范围能涵盖工程设计中绝大部分情况，满足对于试验数据的要求。

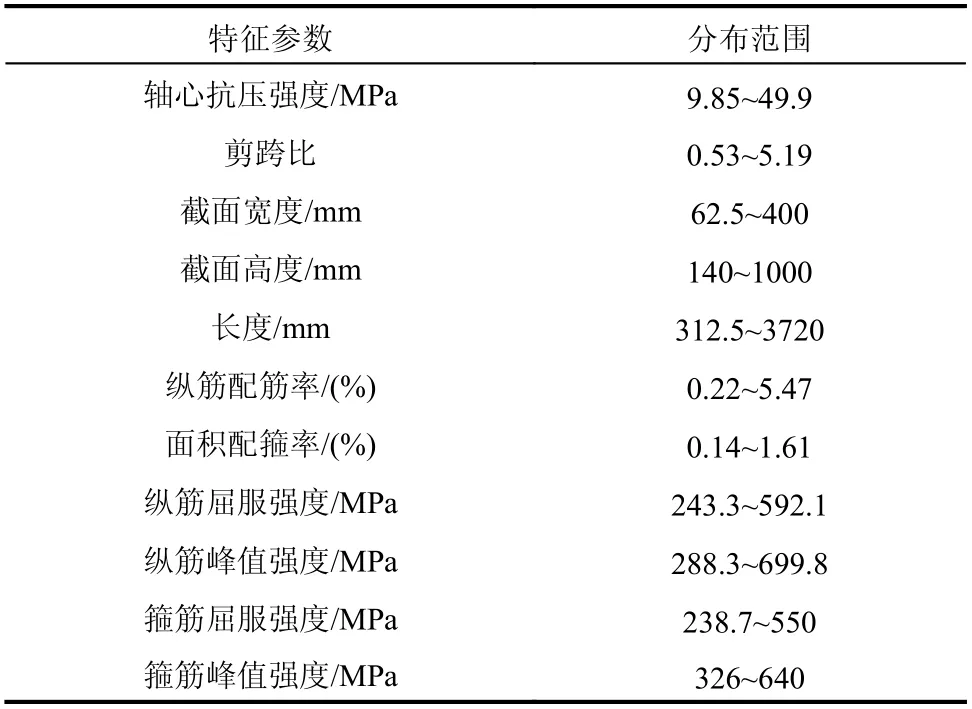
表2 RC 梁试验数据分布情况Table 2 RC beam test data distribution

试验数据中包含有悬臂式(C)、双曲率式(DC)及双简支式(DE)3 种低周往复加载模式。为了对试验数据进行统一的整理和利用，将梁试验均简化为等效悬臂式，等效悬臂高度为试件弯矩最大点与弯矩为0 点之间的距离。对于按悬臂方式加载的试件，试件的等效悬臂高度为试件的悬臂高度；对于按双曲率方式加载的试件，等效悬臂高度则为整个试件高度的1/2，提取的位移为试验位移的1/2；对于双简支式加载的试件，提取的荷载为试验荷载的1/2。在此原则上对试验结果的滞回曲线和骨架曲线进行数据提取，最终建立数字化RC 梁试验数据库。

3 基于试验数据的Pinch-IMK 模型参数辨识

为建立基于Pinch-IMK 集中塑性铰RC 梁构件参数预测模型，需根据构件试验数据对Pinch-IMK 模型参数进行辨识，形成可用于神经网络模型训练及测试的数据集。本文将对骨架参数进行常规几何算法辨识，对滞回参数进行参数筛选，选出4 个关键滞回参数，以误差公式为参考进行参数辨识。

3.1 骨架参数辨识方法

根据构件滞回试验数据，将每一加载级首个滞回环的最大位移点连线即为试验骨架曲线。Pinch-IMK 为三折线本构模型，采用通用的三折线骨架曲线拟合试验骨架曲线即可通过计算得到Pinch-IMK 模型骨架参数。为提高适用性，本研究对三折线骨架特征点参数进行辨识，而需要确定的三折线骨架特征点参数有屈服承载力My、屈服转角θy、峰值承载力Mc、峰值转角θc和残余承载力Mr=0 所对应的转角θr，共分为上升段和下降段2 部分进行。

如图3(a)所示，已知Mc和θc，通过能量等效原理求解未知量My及θy，即以试验曲线及拟合曲线与X轴包围面积相等，如式(1)所示，且使试验曲线及拟合曲线间阴影面积E最小为目标求解，如式(2)和式(3)所示。

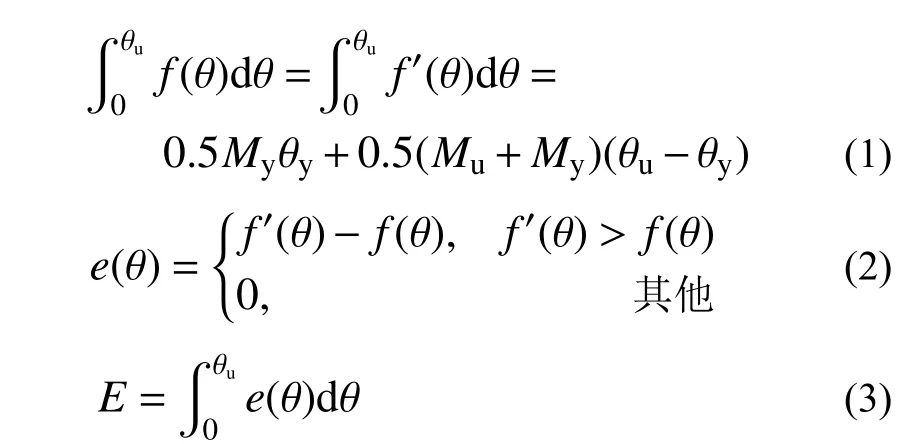
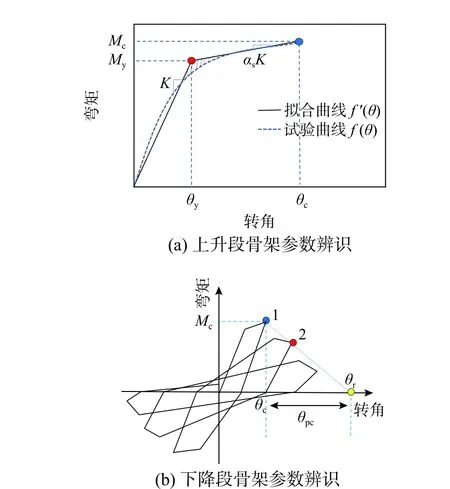
图3 骨架特征点参数辨识Fig. 3 Skeleton feature point parameter identification

如图3(b)所示，曲线下降段有1 个未知量，即残余承载力Mr=0 所对应的变形值θr。以软化斜率最小为目标，取下降段内第一圈滞回环的最大位移点与峰值承载力对应点连线斜率为下降段斜率。下降段内的退化则通过滞回退化参数考虑。

采用上述方法对每根梁的5 个骨架参数进行辨识，建立对应骨架参数的深度神经网络数据库。

3.2 滞回参数辨识方法

滞回参数无明确的物理意义并且参数数量较多，因此难以用常规方法对其进行辨识，故基于误差公式(4)进行参数辨识，在保证拟合效果的同时兼顾参数辨识效率。本文首先对表1 中的12 个滞回参数进行参数筛选，选出关键滞回参数。

本文基于低周往复试验数据对骨架曲线以及滞回参数进行预测，当变形较大时，往复加载得到的骨架曲线相对于单调骨架曲线延性更小，承载力下降更明显。并且由于该模型是基于历史滞回耗能计算后续的强度和刚度的退化，当以较小变形进行多次同级循环加载后，下一级加载会出现较大的刚度和强度退化，不符合实际试验结果。

本文不考虑基本强度退化参数λS和峰值后强度退化参数λC的影响，退化参数λ 的影响与数值大小呈负相关，因此取λS、λC= 100，主要通过再加载刚度退化对滞回曲线的退化进行控制。再加载刚度退化的退化效果基于历史滞回耗能随着加载级数的累积增大而逐步放大，符合实际的试验结果。通过图4(a)和图4(b)的对比可知，不考虑参数λS、 λC的滞回曲线贴合基于低周往复试验提取的骨架曲线，同时有效解决小变形下多次循环加载造成较大退化的问题。

图4 λS、λC 对计算模型的影响Fig. 4 The influence of λS, λC on the calculation model

基于误差公式(4)对剩余8 个滞回参数进行影响性分析，即对目标参数数值分别进行20%和10%的增加和减少，观察计算结果误差的变化幅度，从而判断该滞回参数对模型计算的影响程度。分析过程发现卸载刚度退化指数CK对拟合结果影响较小，且当其取值较小时易出现沿骨架曲线路径退化的无效结果，故不考虑CK参数影响。其他参数影响程度见图5，滞回参数λA及CA对退化效应影响较显著并且取值越小影响越显著，捏拢参数对滞回耗能影响较显著，根据影响分析筛选出4 个关键参数，分别为λA、CA、Fpr和Ap。

图5 滞回参数影响分析Fig. 5 Hysteresis parameter influence analysis

对于其他滞回参数取值为λS、λC=100，λK、CS、CC、CK、D+、D-=1，通过控制4 个关键参数建立Pinch-IMK 模型对不同类型的RC 梁试验滞回曲线进行拟合，情况如图6 所示，能够很好地表征不同类型RC 梁的滞回特性。因此基于试验数据，对每根梁的4 个关键滞回参数进行辨识，建立对应滞回参数的深度神经网络数据库。

图6 Pinch-IMK 模型拟合梁试验滞回曲线Fig. 6 Pinch-IMK model simulating hysteresis loops of experimental data

4 深度前馈神经网络的训练及结果分析

4.1 深度前馈神经网络的建立

本文采用多层BP 神经网络建立模型参数与梁特征参数的映射关系。分别对5 个骨架特征点参数及滞回参数建立深度前馈神经网络模型并进行训练。为提高模型收敛速度和预测精度，进行以下考虑：事先对数据进行最大值归一化处理；采用MSE 作为算法性能评估指标；采用可根据历史梯度对学习率进行修正，以保持合适的学习率进行训练迭代的Adam 优化器；加入早期停止避免过拟合现象；采用交叉验证的方法，仅需将数据随机划分为训练集和测试集，以充分利用实验数据；选取合适超参数以提高模型性能。

神经网络的超参数包含：学习率、网络层数、单元个数、激活函数等。超参数会直接影响神经网络的预测精度、收敛速度、泛化能力等性能，因此需要确定合适的超参数组合。

先确定超参数的合理取值范围，学习率可取0.0001、0.0005、0.001、0.005、0.01；为避免出现过拟合现象，网络层数不宜太多，可取3 层或4 层；单元个数可取16、32、64、128、256；激活函数可取性能较好的tanh 或Leaky ReLu 函数。基于以上参数取值进行组合，通过网格搜索的方法确定最优超参数组合，即对每种超参数组合建立模型并训练6 次，取平均误差作为该模型的误差，进而找出最优超参数组合。

4.2 特征参数降维

对于神经网络模型，输入参数越多，所需要的样本数量越多，在一定的样本数量下，为使模型更加准确可靠，对输入特征参数进行降维。选出关键输入参数，提高模型的适用性，减少模型复杂度以减少过拟合的风险。本文拟对5 个骨架特征点参数分别建立独立神经网络模型进行训练预测，故需针对不同的骨架参数进行输入特征参数降维。

随着加载位移的增大及循环次数的增多，RC 梁滞回曲线会出现明显的退化，且退化情况与加载历史呈强相关性，导致θr数据具有较大的离散性，难以确定θr的取值。本文采用残余转角系数θr/θc来确定θr，通过将每根梁的θr与自身θc建立关系来保证数据的合理性，再利用神经网络寻找残余转角系数与梁特征参数之间的映射关系。

首先分别选取11 个和14 个特征参数作为输入参数，通过网格搜索，采用5 折交叉验证法确定超参数，建立屈服荷载系数神经网络模型和峰值荷载系数神经网络模型。基于两个模型对屈服荷载系数和峰值荷载系数进行参数影响分析，即打乱目标参数数据排序，基于打乱的数据集对屈服荷载系数和峰值荷载系数进行预测，计算拟合误差，通过误差波动幅值来判断该参数影响大小。

分析结果如表3 所示，由于截面尺寸及配筋信息等参数在截面分析中已被考虑，因此对于荷载系数的影响不明显，而未被考虑的剪跨比和配箍率呈现强相关性，符合经验理论。根据参数影响分析结果，最终确定对于屈服荷载系数的4 个输入参数，峰值荷载系数的3 个输入参数。

表3 特征参数影响分析Table 3 Characteristic parameter influence analysis

基于现有针对RC 梁屈服转角和峰值点对应转角的研究及经验公式[18-20]，分别确定屈服转角和峰值转角的7 个输入特征参数；同样采用参数影响分析的方法，确定对应残余转角系数的7 个输入参数；对应滞回参数神经网络模型则采用11 个输入参数，各目标参数所对应输入参数见表4。

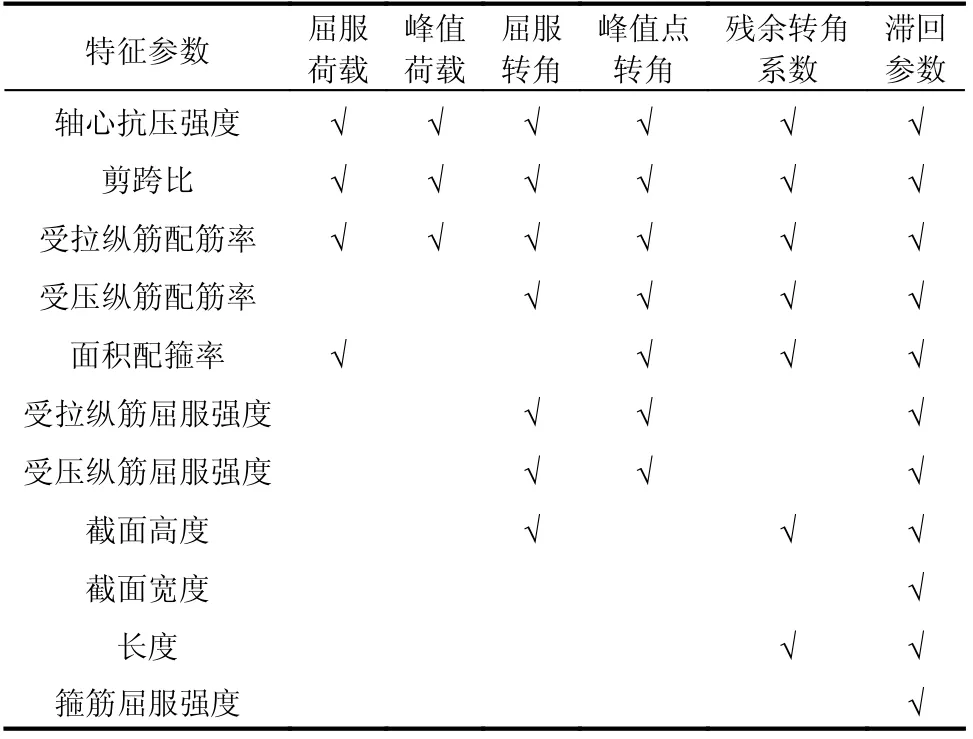
表4 输入特征参数Table 4 Input parameters

4.3 结果分析

通过上述方法最终建立Pinch-IMK 模型参数选取的智能预测模型HDLM，其包含6 个神经网络模型，分别为：屈服荷载系数神经网络模型、峰值荷载系数神经网络模型、屈服转角神经网络模型、峰值转角神经网络模型，训练集均包含162 份样本，测试集均包含20 份样本；残余转角系数神经网络模型，训练集包含103 份样本，测试集包含15 份样本；滞回参数神经网络模型，训练集包含83 份样本，测试集包含8 份样本。神经网络结构如表5 所示。

表5 神经网络模型结构Table 5 Neural network model structure

基于收集的RC 梁试验数据将HDLM 预测骨架参数与现有其他常用方法或经验公式进行对比，结果如表6 所示。可知截面分析对于RC 梁的承载力计算具有一定的精度，其他方法对于RC 梁的转角计算普遍误差较大，由于θpc受加载制度及加载历史影响，因此难以通过公式拟合，而HDLM预测骨架参数相对其他方法具有更高的精度。

表6 采用不同方法计算骨架参数的误差 /(%)Table 6 Skeleton parameter errors calculated by different methods

为更直观表示构建的HDLM 对于RC 梁低周往复加载下滞回曲线的预测情况，选取滞回参数神经网络模型测试集中的8 份样本，基于HDLM预测参数计算滞回曲线，并采用基于经验公式的IMK 模型[19]计算结果作对比。这部分样本包含不同剪跨比、不同配筋率、对称配筋及不对称配筋的RC 梁构件，且该部分样本并未用于所有神经网络模型的训练，仅用于反映模型训练效果，测试模型泛化能力和评估预测结果精度。由于目前尚未有对Pinch-IMK 模型捏拢参数的取值研究，因此采用峰值指向型IMK 模型进行对比计算，骨架参数以及退化参数λ 通过经验公式确定取值，退化指数C均取1。

采用基于经验公式的峰值指向型IMK 模型对8 份样本试件进行计算，计算结果与试验滞回曲线的对比如图7 所示，图中λ 为剪跨比，ρ 为纵筋配筋率。由于基于经验公式计算的转角存在较大误差，计算得到的退化参数λ 数值普遍偏大，导致计算结果下降段与试验不符，且无法模拟RC 梁的退化效应以及剪切型破坏滞回曲线的捏拢效应。

图7 基于经验公式的集中塑性铰模型计算结果与试验结果对比Fig. 7 Comparison of experimental results and calculation results of concentrated plastic hinge model based on empirical formula

通过HDLM 预测8 个样本试件的Pinch-IMK模型参数，建立Pinch-IMK 集中塑性铰模型进行计算分析，计算结果与试验滞回曲线进行对比，结果如图8 所示。

图8 HDLM 预测结果与试验结果对比Fig. 8 Comparison of the predicted hysteresis loops using the HDLM prediction parameters and experimental results

对比可知，HDLM 预测模型能够很好地对Pinch-IMK 模型参数进行预测，HDLM 预测骨架特征点参数相比于经验公式和截面分析具有更高的精度，预测滞回曲线与试验曲线吻合良好，可以较好地模拟构件的承载力、捏拢效应和退化效应，较基于经验公式的集中塑性铰模型具有更好的模拟效果。且试验数据库中构件剪跨比范围为0.53～5.19，涵盖弯曲破坏、剪切破坏及弯剪破坏3 种不同破坏类型的RC 梁构件，结果表明模型能够较好地预测不同破坏类型的RC 梁在低周往复加载下的滞回曲线。基于HDLM 的RC 梁滞回曲线预测结果表明，该预测模型具有计算速度快、计算精度高、使用范围广的特点，证明了该方法准确可靠。

5 结论

本文基于91 根RC 梁低周往复试验数据，对Pinch-IMK 模型本构骨架参数和滞回参数进行辨识，并建立Pinch-IMK 集中塑性铰RC 梁构件参数深度学习预测模型。本文结论如下：

(1) 基于91 根RC 梁低周往复试验数据，通过深度前馈网络建立RC 梁构件特征参数与Pinch-IMK 模型参数之间的非线性关系，进而建立Pinch-IMK 模型参数选取的智能预测模型HDLM。

(2) HDLM 预测骨架特征点参数相比于经验公式和截面分析的结果具有更高的精度；预测滞回曲线与试验曲线吻合良好，较基于经验公式的IMK 模型具有更好的模拟效果，可以较好地模拟构件的承载力、捏拢效应和退化效应，该方法适用于预测剪切破坏、弯曲破坏及弯剪破坏的RC 梁滞回曲线。