射孔套管极限承载力计算二次开发研究

曹先凡，刘美会，赵开龙，姚志广

1.中国石油集团工程技术研究有限公司，天津 300451

2.中国石油天然气集团公司海洋工程重点实验室，天津 300451

射孔套管在油气开采中受到内压[1-3]、外压[4-6]、拉力[7-8]、弯矩和温度[9-10]等载荷的作用，可能产生强度[1，3-7，9-10]、断裂[2，8]、屈曲[11-12]等形式的破坏。

本文给出射孔套管极限承载力计算流程，建立射孔套管数值模型，基于Python进行ABAQUS二次开发，实现射孔套管极限承载力的自动计算，给出特定射孔模型对应的抗外压、抗拉和抗弯能力，以及外压+拉力、外压+弯矩、拉力+弯矩和外压+拉力+弯矩等联合载荷下的极限承载力[13-22]。

1 射孔套管极限承载力评价方法

本文以射孔套管屈服强度对应的载荷为极限承载力，其计算流程见图1。首先根据射孔套管材料、外径、壁厚、射孔空间分布、射孔尺寸等参数建立数值模型，施加初始载荷得到其应力分布，选取最大应力σi与屈服强度σ0比较，如果差别较大，则根据特定算法调整载荷，重新计算射孔套管应力，直至最大应力达到屈服强度，此载荷即为极限承载力。

图1 射孔套管极限承载力计算流程

2 数值模型

2.1 建立方法

射孔套管数值模型有两种建模方法：第一种方法基于ABAQUS CAE模块建立计算模型，包括套管和射孔模型建立、几何模型运算以及载荷与边界条件设置等，然后采用Python调用该模型并修改相关参数；第二种方法完全基于Python编程建立套管和射孔模型，进行几何模型运算，以及施加载荷与边界条件等。第一种方法可以利用现有的交互式界面，参考资料丰富，建立模型方便。第二种方法需要熟悉Python语言和ABAQUS软件架构，较为复杂，但可以控制更多的参数。在需要参数化建模或者针对管径、壁厚、孔径、孔数、射孔分布等参数优化时，采用第二种方法更合适。本文目标是建立特定射孔形式套管的极限承载力求解方法，因此选取了第一种方法建立数值模型。

射孔套管的主要几何参数见表1，其外径为210 mm，壁厚为10 mm；套管每隔3 m在同一个圆环上布置6个圆孔，每个圆孔环向间隔60°，圆孔直径为16mm。套管管材为P110钢，弹性模量为210 GPa，泊松比为0.3，屈服强度为758 MPa，假设其为理想塑性材料。

表1 射孔套管主要参数

根据射孔套管主要参数建立数值模型，见图2。由射孔套管结构特点可知，危险点位于圆孔附近，为了避免边界对计算结果的影响，令长度与外径之比大于3，模型长度选择为1.5 m。可以采用实体单元或壳单元离散射孔套管模型，实体单元可以直观展示径向应力分布，但计算量大；壳单元适用于厚度远小于面内尺寸的结构，可大幅提高计算效率，通过设置厚度方向的积分点数目，可确定厚度方向的应力变化。如图3所示，本文根据射孔套管结构特点选择壳单元离散模型，在厚度方向设置5个积分点；为了精确得到射孔区域的应力，并降低计算量，在射孔附近采用密集网格，而在其他部分采用稀疏网格。图4给出了边界条件施加方法，在模型两端分别设置参考点，参考点分别与相应端面绑定，在一端参考点施加固支约束，另一端参考点施加载荷。

图2 射孔套管数值模型

图3 射孔套管有限元离散图

图4 射孔套管边界条件示意

数值模型保存为*.cae文件，通过指定文件路径“*:/NAME/”以函数openMdb调用该模型，函数如下：

2.2 单元集定义

既可以在整个模型中计算最大应力σi，也可以根据结构特点，缩小搜索区域。前者适合于结构、载荷、边界条件复杂，难以确定最大应力位置的模型，后者用于已确定最大应力区域的结构。根据射孔套管结构特点，其最大应力处于射孔附近。文中将6个射孔附近单元定义为单元集Set-EL，见图5。

图5 单元集区域示意

程序段如下所示：

2.3 载荷调整

载荷既可为外力也可为位移，一般情况下非线性分析时施加位移载荷更易于收敛，本文采用了位移载荷，其定义和调整程序段如下：

2.4 最大应力计算

2.5 极限承载力迭代计算

采用迭代法使最大应力逼近材料屈服强度，得到射孔套管的极限承载力。迭代法主要有切线法和割线法，其中切线法速度快，但需要求解导数；割线法计算慢，但割线斜率易于求解。由于文中最大应力关于载荷的导数难以求解，故选取了割线法，见图6。

图6 割线法示意

如图1所示，某载荷作用下的最大应力与材料屈服强度之差小于一小量时，则认为两者相同，该小量越小越好，考虑计算效率，选择为屈服强度的万分之一。

载荷调整方法见下式：

式中：θi+1为第i+1步载荷，θi为第i步载荷，σi为第i步的最大应力，σ0为材料屈服强度。

载荷调整程序如下：

3 极限承载力分析

3.1 抗外压能力

根据以上分析方法，计算射孔套管抗外压能力。当外压为23.84 MPa时，射孔套管圆孔附近的应力达到屈服强度，计算结果见图7，可知该射孔套管抗外压能力为23.84 MPa。

图7 外压作用下射孔套管应力/Pa

3.2 抗拉能力

根据以上分析方法，计算射孔套管抗拉能力。当拉力为1 713 kN时，射孔套管圆孔附近的应力达到屈服强度，计算结果见图8，可知该射孔套管抗拉能力为1 713 kN。

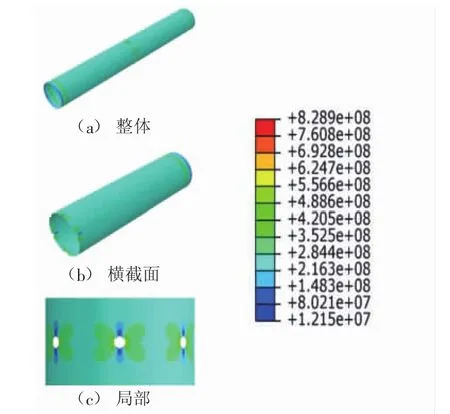
图8 拉力作用下射孔套管应力/Pa

3.3 抗弯能力

根据以上分析方法，计算射孔套管抗弯能力。绕X轴施加转角，当转角为0.75°/m、弯矩为88.27 kN·m时，射孔套管顶部和底部圆孔附近的应力达到屈服强度，计算结果见图9，即该射孔套管抗弯能力为88.27 kN·m。

图9 转角（弯矩）作用下射孔套管应力/Pa

3.4 联合载荷作用下的极限承载力

射孔套管服役中往往承受外压、拉力和弯矩的联合作用，为了保障结构安全，本文研究了联合载荷作用下结构的承载力。外压+拉力、外压+弯矩、拉力+弯矩等载荷作用下的包络线分别见图10（a） ～（c），当两种载荷构成的坐标位于包络线之下，则结构是安全的；外压+拉力+弯矩等联合载荷作用下的极限承载力安全面如图11所示，当三者构成的坐标位于安全面之下时，则结构是安全的。

图10 承载力包络线示意

图11 外压+拉力+弯矩作用下承载力安全面示意

4 结论

（1）基于ABAQUS CAE建立射孔套管数值模型，以Python编写模型调用程序，利用割线迭代法搜索射孔套管极限承载力，实现射孔套管极限承载力计算的自动化，提高了分析的效率。

（2）利用建立的二次开发程序，分析了射孔套管在外压、拉力和弯矩单独作用下的响应，得到了抗外压、抗拉和抗弯能力；考虑射孔套管服役环境的复杂性，计算了外压+拉力、外压+弯矩和拉力+弯矩等载荷联合作用下极限承载力的包络线以及外压+拉力+弯矩作用下的安全面，验证了二次开发程序的有效性，为射孔套管极限承载力的参数优化奠定了基础。