吸附塔球封内件支撑环结构优化分析
郝明涛,江保全,李宗伟,张杰
(1. 西南化工研究设计院有限公司,成都 610065;2. 合肥通用机械研究院特种设备检验站有限公司,合肥 230031)
吸附塔是变压吸附制氢装置中的关键设备,多台规格相同的填料塔内,交替循环进行“吸附→顺放→逆放→解吸”的过程。由于循环周期短,在设计使用年限内,塔内压力循环次数通常高达百万次。在长期的交变应力作用下,由于晶间滑移和位错运动容易萌生微裂纹,微裂纹在载荷循环下不断扩展,最终导致整个截面疲劳断裂丧失承载能力。为改善设备受力情况,保障装置的的安全运行,对于压力波动范围大、循环次数高的工况,吸附塔上下封头通常采用球形封 头。
为了保障气流与吸附剂的均匀接触,同时有效利用封头空间。通常将吸附剂支撑结构设置于封头内壁,由此封头内表面不可避免地出现角焊缝,从而产生应力集中,影响设备的疲劳寿命。分析设计方法应用之前,吸附塔承压壳体厚度取值通常较为保守,内件支撑型式及几何参数的合理性问题,在大裕量设计情形下很难暴露出来。随着设备大型化的发展,保守取值往往会显著增加设备成本。安全性与经济性并重的要求下,就要求设计源头对每一个高应力危险区域进行精确分析,以便设计出安全、经济、便于制造、易于安装和检验的结构。
疲劳强度减弱系数反映角焊缝对局部不连续区疲劳寿命的影响程度。角焊缝的疲劳强度减弱系数与焊接接头是否全焊透,是否经过机械打磨,是否做过无损检测以及做了何种无损检测息息相关。不同制作情况下的系数取值差异较大,标准中提供的常见取值为1.5、1.7、2.0、3.0、4.0[1]。因此,垫板、拉筋等传统未焊透角焊缝连接方式都不宜采用。本文给出了一种与封头焊透的全新支撑环结构,并采用ANSYS中响应曲面(Response Surface)优化设计模块探讨支撑环几何参数,对球形封头支撑环的结构不连续区的最大应力强度的影响规律。
1 模型分析
1.1 设计条件
本文以DN 1 400 mm 吸附塔,带全焊透支撑环的上部球形封头为研究对象,封头与支撑环材质均为Q345R,操作压力为0.02 ~ 1.8 MPa,操作温度为20 ~ 40℃,压力循环次数为8.0×105,结构如图1 所示。

图1 模型结构示意Fig.1 Schematic of model structure
1.2 边界条件
(1)封头中心线厚度方向沿界面对称约束,封头水平方向沿厚度界面的法线方向位移为零。
(2)封头内表面仅承受垂直于表面的内压,为简化分析,文中仅计算最大操作载荷下模型的应力强度最大值,用于疲劳寿命判定。
(3)忽略内件重力对支撑环的影响。
(4)支撑环远离球封结构不连续区,根据圣维南原理,筒体及封头中心开孔对支撑环的局部峰值应力不会产生影响,模型简化为带支撑环的半球形封头,如图2 所示。

图2 模型边界条件图Fig.2 Boundary condition of model
2 结构优化
2.1 优化方法
优化作为一种数学方法,通常是利用对解析函数求极值的方法来达到寻求最优值的目的。基于数值分析技术的 CAE 方法,通过多个数值点利用插值技术形成一条连续的可用函数表达的曲面(或曲线),当插值点样本足够多时,可以用样本值点形成的曲面近似代替目标曲面,该曲面的最小值便可以认为是目标最优值[2]。
ANSYS DX 是一个基于参数的设计探索及优化模块,其中响应曲面法(Response Surface)在实验设计组件(Design of Experiments)定义设计空间。文中采用软件缺省的中心组合实验法(Central Composite Design)对设计空间进行采样。根据输入参数的数目,利用蒙特卡罗抽样技术,采集设计参数样点,计算每个样点的响应结果,利用二次插值函数构造设计空间的响应面或设计曲线。采用响应面法,可用较少的试验次数响应复杂的工程设计问题,减少有限元数值分析的次数[3]。
2.2 目标函数
由图1 可知,影响封头支撑环峰值应力的几何结构参数:封头厚度;支撑环厚度T;支撑环角度A;内侧焊角r;外侧焊脚R。降低峰值应力最简单的办法是直接增加封头厚度,从源头上减少封头内压作用下封头的形变量,结构突变区域产生的峰值应力也随之降低。但是,增加壁厚使得设备重量显著增加,经济性变差。着眼于支撑环局部结构尺寸优化便成为了首选,即在T、A、r、R组成的设计空间内,找出各设计变量对最大应力值的变化规律,并选择一组或几组适用于工程设计参数组合。
支撑环结构优化问题可以表示为如下数学优化模型[2,4]:

式中,目标函数σ代表应力强度最大值,约束条件为满足疲劳工况的最大应力强度,S为设计变量的搜寻区域。
2.3 设计变量设置
设计变量的初始值,以及各参数的取值范围见表1。

表1 支撑环几何参数初值及取值范围Table 1 Initial value and value ranges of geometry parameters for supporting ring
2.4 状态变量设置
优化目标函数为第三应力强度(Intensivity Stress)的峰值最小,约束条件见表2。

表2 支撑环优化约束条件Table 2 Optimal constraint condition of supporting ring
3 中心组合试验
中心组合设计方法其样本点包括一个中心点,输入变量轴的端点以及水平因子点。实验数据如表3所示。

表3 中心组合实验数据Table 3 Central composite design data
图3 表明,在试验点12 处的应力强度极值最小,在试验点22 处的应力强度极值最大。综合表4,试验点12 处的应力强度极值为134.751 MPa,参照ASME 标准疲劳曲线,许用循环次数约为1.2×108。试验点22 应力强度极值为186.046 MPa,按照JB/T 4732 许用循环次数约为5×105。考虑不带支撑环时,该工况下封头远离不连续处的薄膜应力约为79.2 MPa,试验点12 和试验点22 对应应力集中系数分别为:1.7、2.35,两者理论疲劳寿命差距近240 倍。
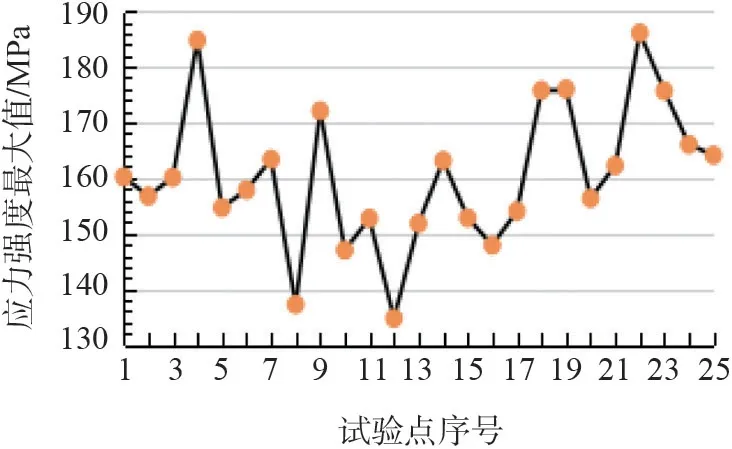
图3 试验点应力强度最大值分布图Fig.3 Maximum stress intensity distribution of experiment design points
4 实验结果
4.1 参数灵敏度分析
图4 表明:T、r、A与结构不连续区的峰值应力正相关,即支撑环厚度、内侧焊脚圆弧、支撑环锥度增加,结构应力强度最大值增大,且三个变量对峰值应力的影响力T>r>A,其比重大约为:58%、28%、10%;R与结构不连续区的峰值应力负相关,即外侧焊接圆角R增大,结构应力强度最大值减小,其相对影响比重约为24%。
4.2 参数对优化目标影响曲线
图5 在水平线上下两侧的曲线,再次印证了图4 中设计变量对结构峰值应力的影响关系。P5-T、P5-r、P5-A 三条递增曲线表明,随着参数值的增加,峰值应力增大,即变量与目标函数正相关。而且,位置越高的曲线所对应的参数的变化,对应力强度最大值的影响也越大。P5-R 递减曲线表明,随着参数值的增加,峰值应力减小。

图4 设计变量参数敏感度柱状图Fig.4 Sensitivity histogram of design variable parameter
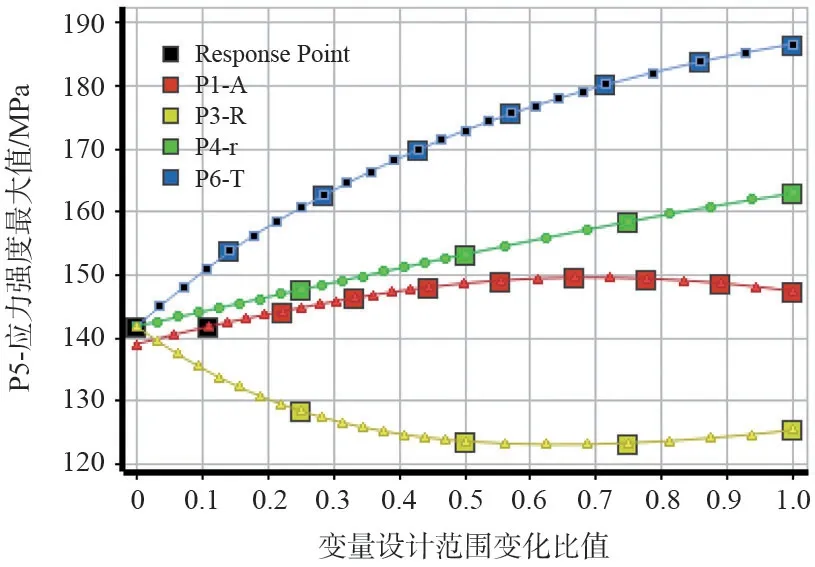
图5 设计变量对应力强度最大值的响应曲线Fig.5 Response curve of design variable to maximum stress intensity
此外,从曲线的斜率变化可以反映出:在所定义的设计空间范围内,目标函数对设计变量的变化快慢不同。P5-T 响应曲线的斜率逐渐减小,表明在厚度增加相同比例的情况下,峰值应力增加的比例在逐渐减小。从P5-r 响应曲线近似为一条斜线,表明在r增加相同比例的情况下,峰值应力增加百分比几乎相同。P5-A 和P5-R 的响应曲线并不完全是一条单调递增或递减的曲线,曲线上均存在拐点。在设计空间40% ~ 80%的范围内,峰值应力变化曲线的斜率几乎为零,表明在该范围区间内,应力强度最大值对这两个参数的这两个参数的变化不敏感。
4.3 响应曲面值与中心组合试验点计算值比较
见图6。
4.4 目标函数极值
通过响应曲面的参数输出模块,查看目标函数在设计空间下的最大值和最小值,如图6 所示。

图6 响应曲面和设计点应力强度最大值比较Fig.6 Maximum Stress intensity comparison between the response surface and design points
由表4 可知,表1 所定义的设计空间下支撑环处的应力强度极值中,最大为201.83 MPa,最小为123.33 MPa,应力集中系数范围为1.56 ~ 2.55。

表4 目标函数极大值和极小值Table 4 The maximum and minimum value of target function
5 结论
球形封头支撑环处局部最大应力值调整时,降低最大应力值的办法:减少支撑环厚度T;减小内侧焊脚圆弧r;减小支撑环角度A;增大外侧焊脚圆弧R。为快速确定满足工程设计的参数,建议调整优先顺序依次为:T、r、R、A。而且A对最大应力值影响最小,应主要结合制造情况确定。
6 建议
支撑环与封头的焊接接头质量是保证疲劳设备安全的关键因素,支撑环尺寸结构需要考虑焊接施工难易程度,焊缝机械加工或者打磨操作难易程度,以及无损检测难易程度。此处的焊接接头的无损检测建议按A 类焊缝考虑,采用100%RT + 100%MT(PT)+ 100%VT 的方式检测,以保证焊接接头质量[5]。
A对峰值应力变化影响很小,建议该参数的选取结合制造过程中成型难易程度确定。另外,焊脚成型过程中,除非采用机械加工的方式,往往很难打磨出理想的圆角尺寸。而且,从图5 可以看出,减小r不仅可以降低制作过程中的焊接量,还可以改善最大应力值。同样,对于R,虽然在小范围内增加会降低最大应力值,但超过约50%的变化范围后,增大R同样会增加焊接工作量和打磨工作量。因此,在图纸设计过程中建议内侧圆角r标注上限,外侧圆角R标注下限。如果标注某一确定值,在设备出厂验收时,在保证焊接接头质量的情况下,技术人员可以参考文中揭示规律评估焊脚尺寸对疲劳寿命的影响。

