高超声速喷管设计理论与方法
汪运鹏 姜宗林
中国科学院力学研究所, 高温气体动力学国家重点实验室, 北京 100190
1 引 言
钱学森先生在谈到我国风洞建设事业时说: “我始终认为, 空气动力学的研究及其相应试验设施的建设, 是我国航空航天事业中不可缺少的一项重要工作” (张涵信 2004). 风洞试验设备对航空航天技术发展和飞行器研制至关重要, 特别是高超声速飞行器的风洞试验和高焓气体流动相关的研究, 对高超声速风洞性能提出了更高的研发要求. 高焓流动的模拟能力需要风洞喷管流动不仅满足高马赫数 (一般 ≥5)条件, 还要确保试验气体具有足够高的焓值可以产生明显的高温气体效应. 一些学者通常采用“hypervelocity” (超高速)来描述这种流动 (Stalker 1989), 以便区别于传统高超声速风洞的低声速高马赫数流动.
Stalker (1989)认为模拟高温真实气体效应最成功的地面试验设备是基于反射型运行模式的激波风洞. 这种模式实现了高温气源的“即生即用”, 大大降低了风洞的热负荷. 20世纪60年代中期以来, 国际上发展了多种强驱动方式来提高激波风洞的性能. 其中, 自由活塞驱动和爆轰驱动等成为高焓风洞的主要驱动运行方式. 采用Stalker (1967)提出的自由活塞驱动技术, 压缩和加热实验气体可实现7 ~ 8 km/s的试验气流速度, 其焓值最高可达40 MJ/kg. 但其有效试验时间仅为1 ~ 3 ms, 对流动测试技术发展构成巨大的挑战. 尽管如此, 自由活塞激波风洞仍然以其能同时产生高雷诺数和高马赫数实验流动, 模拟高超声速飞行器在地球大气层中的高温飞行环境, 成为研究真实气体效应最为广泛的设备之一 (徐立功 1992). Bird (1957)首先提出了应用爆轰驱动激波管产生高焓气源的基本思想, 随后对驱动段末端和主膜处起爆的驱动方式分别进行了计算和分析. Yu等(1992)提出在驱动段末端增加卸爆段装置以消除反射超高压造成的高载荷风险, 从而使爆轰驱动方法可用来产生高焓试验气流. 姜宗林等(2012)提出长实验时间激波风洞理论, 把反向爆轰驱动激波风洞的实验时间延长到130 ms. 由此研制成功JF-12复现风洞, 能够再现飞行马赫数5 ~ 9, 高度25 ~ 50 km的飞行条件 (Jiang et al. 2017). 但是, 相对常规高超声速风洞, 激波风洞的有效试验时间依然非常短, 因此能否迅速得到高品质试验气流成为风洞研制成功与否的关键因素之一. 对于高焓激波风洞, 还需要考虑高温真实气体效应对于喷管型线的影响, 因此借助传统方法设计的高超声速风洞喷管要通过型线修正才能得到较好品质的高焓试验气流.
20世纪20年代, Prandtl和Busemann (1929)提出了特征线方法 (method of characteristics,MOC), 为现代风洞喷管设计奠定了理论基础. 许多超声速、高超声速风洞的喷管大多是基于MOC方法设计的. 到20世纪四五十年代, 发展了多种图解方法设计高速喷管 (Busemann 1931,Preiswerk 1940, Puckett 1946). 但是随着对喷管流场品质要求的提高, 图解法设计的高速喷管不再能满足设计需求. 基于特征线方法, 也发展了多种喷管设计的多种解析方法 (Foelsch 1946,1949; Cresci 1958; Sivells 1969, 1970, 1978). 这类方法基于理论源流假设, 采用理论和经验公式, 通过MOC方法计算得到喷管型面曲线. 其中, Sivells提出基于轴向马赫数分布的设计方法, 使喷管流场品质得到改善, 成为经典的高速喷管设计方法, 并沿用至今.
随着人们对高超声速飞行技术的深入探索, 高温真实气体效应在飞行器气动特性方面的显著影响使得高焓流动受到广泛关注. 20世纪四五十年代开始, 人们探索高焓喷管设计方法, 以获得高品质的高超声速试验流场. 最早的高焓喷管设计仅仅关注比热比γ变化的影响 (Guentert et al.1959, Enkenhus et al. 1962), 型线计算依然采用MOC方法. 实践表明对于高焓喷管设计仅考虑γ变化会产生一定的设计误差, 尤其是对于超高速喷管, 这种误差变得难以接受. 于是人们采用CFD (computational fluid dynamics)数值计算技术进行型线计算和优化, 以达到提高喷管流场品质的要求. 90年代初, MOC方法在高超声速喷管设计中的局限性问题得到进一步的认识, MOC方法对马赫数在8以下的喷管设计是有效的, 对于更高马赫数的喷管则建议通过求解抛物化的Navier-Stokes (PNS)方程进行型线设计 (Benton 1990). 已经有许多CFD计算技术用于高超声速高焓喷管的优化设计工作 (Korte 1992a, 1992b, 1992c, 1992d, 1993, 1994, 1995, 2000; Keeling 1993;Tolle 1997; Shope 2006; Chan et al. 2018), 他们把不同的优化算法耦合到CFD求解器中, 然后进行自动迭代求解与优化选型. CFD求解器耦合优化方法使得超高速喷管的流场品质得到了较大的提升, 但其计算程序和优化流程非常复杂, 求解器的鲁棒性也参差不齐. Gaffney (2006)和唐蓓等(2019)把CFD求解器与优化方法的计算过程解耦处理, 在保障喷管设计效率和流场品质的同时, 使设计流程复杂程度大大降低, 便于工程推广应用.
关于风洞喷管设计理论与方法的文献多发表于20世纪70年代以前, 由于受到计算机技术的限制, 当时的研究偏重于解析和半解析的方法. 随着计算机和CFD技术的发展, 对喷管流动实现了更加精确的计算模拟, 使得CFD计算技术辅助的优化设计方法得到广泛关注 (易仕和等2013). 针对高焓风洞喷管的设计方法也得到发展, 提出了一些改进的设计理论和高温气体效应的修正方法. 但是, 由于高温反应气体流动的复杂性, 及其非平衡流动的物理化学特性模拟方程的局限性, 高品质的高焓喷管设计依然是一个难题. 而且, 随着流动马赫数和焓值的提高, 实际得到的试验流场参数与设计结果存在着偏差较大的问题. 高超声速飞行技术是将来宇航工业的核心技术, 风洞实验是其主要的研究手段, 所以关于高超声速喷管设计理论与方法的研究具有重要的意义.
2 高超声速喷管设计的基础与问题
在激波风洞这样的脉冲型风洞设备中, 喷管被放置在被驱动段管道与试验段之间, 空气在被驱动段内通过激波加热, 产生的高温高压气体通过喷管膨胀加速抵达试验段, 形成均匀稳定的试验气流 (见图1). 喷管型面设计与被驱动段、实验段的几何布局和热力学状态密切相关. 本文仅关注二维轴对称喷管设计和高焓流动问题, 也是其他类型喷管设计的基础.
被驱动段的驻室条件是由入射激波的反射决定的, 是一种高温反应气体. 因此, 高焓风洞喷管的膨胀加速流动具有复杂的物理化学反应机制和高温气体效应, 使得计算模拟和试验测量均难以准确评估. 所以, 早期喷管设计方法都采用准一维化学平衡流动模型进行分析. 如果再假定高焓流动无黏绝热时, 那么平衡化学反应喷管流动是等熵的. 在喷管流动分析中,等熵流动的结论可以用来代替动量方程或者能量方程. 通常, 平衡化学反应并不会引起系统不可逆, 即如果一个反应平衡系统在压强和温度分别为 p和 T的初始条件下, 由于某种条件变化发生偏离, 但最终状态仍然回到 p和 T, 那么化学成分也变成初始状态时的组成. 在平衡化学反应是可逆的条件下, 任意无激波、无黏、绝热的平衡化学反应流动都是等熵的 (童秉纲等1990). 在局部热力学和化学平衡条件下, 二维轴对称喷管流动可简化为准一维流动, 其截面积是一个变量A=A(x), 但所有的流动参数在任意截面上都是一个确定的常数. 在任意给定位置的流动参数和面积比A/A∗依赖于3个参数, 即p,T和当地速度u, 且满足下列公式 (Anderson 2006)

而对于量热完全气体 (比热容比γ=1.4时), 喷管流动的性质仅依赖于当地马赫数, 即
UCT 算法 (Upper Confidence Bound Apply to Tree),上限置信区间算法,UCT算法是一种特殊的蒙特卡罗搜索算法,它有三个部分:树选择策略,默认模拟策略和模拟结果。

因此喷管平衡流动可被简化为等熵的准一维流动, 并探究其膨胀流动特性和规律, Anderson(2006)在他的著作中给出了详细的证明. 然而, 当喷管流动是非平衡的时候, 上述结论是不成立的.
非平衡过程的影响使高焓风洞喷管设计产生诸多的不确定性. 面对非平衡流动的复杂性,Hall和Treanor (1968)的喷管流动分析仅限于定常状态. 1969年, Anderson (1970a, 1970b)提出一种新的非平衡喷管流动的求解方法, 涉及到非定常状态. 该方法利用时间推进有限差分方法求解, 规避了关于定常假设分析存在的问题 (Anderson 2003). 在诸多的文献和著作中, 非平衡流动的分析方法都是假定喉道处达到当地平衡, 然后从喉道下游开始非平衡计算. 这种方式避开了带有鞍点奇异性和未知质量流的问题, Erickson (1963), Harris和Albacete (1964)进行了详细的分析和讨论. 在喷管设计理论与方法研究中, 二维轴对称非平衡喷管流动通常采用MOC方法(Prandtl & Busemann 1929)或者CFD数值方法求解. 由于在非平衡流动中, 沿流线的熵增是有限速率反应过程的不可逆因素的结果, 因此采用非平衡MOC方法时需要注意的是, 通过非平衡超声速流动任意一点的特征线是基于冻结声速的马赫线和流线. 关于应用MOC方法详细求解非平衡流动过程可参见Zucrow和Hoffman (1997)的文献. 对于高超声速喷管设计, 随着马赫数的提高, MOC方法表现出了一些理论上的局限性. 全流场求解的CFD数值计算技术在喷管设计中得到越来越多的应用, 但是随着超高速气流焓值的增加, 目前化学反应模型的准确性和CFD数值求解技术同样表现出了一些局限性, 尤其是针对极高马赫数的高焓流动. 所以, 高超声速高焓喷管设计仍然存在一些难点和问题没有得到有效的解决.
2.2 产后2 h阴道出血量 48例患者中有45例出血量为50~100 ml,2例出血量为150~200 ml出血量,1例出血量250~300 ml。
(1) 目前的高超声速喷管设计仍然使用或参考几十年前的传统方法, 只是由于计算技术的发展, 使得某些方法的计算成本降低了. 相当一部分传统方法中的假设条件对高超声速和高焓流动是不适用的, 亟需针对高焓流动喷管设计发展新的、有效的理论和方法;
(2) 在高焓喷管流动中, 气体的比热比是一个变量. 高温、化学反应、非平衡流动等问题在高焓喷管流动中也产生了较大的影响, 并且随着流动速度的提高, 高温气体效应影响也越来越大;
(3) 利用传统方法设计的高超声速喷管较长, 尤其对于超高速喷管. 由于喷管出口流动均匀区 (通常称为菱形区)本身就很长, 使得目前的短化技术也无能为力. 超长的喷管导致出口边界层厚度增大, 甚至超过喷管出口截面积的50%. 此外, 目前的计算技术对高焓流动边界层的发展(流态以湍流为主)难以做到准确评估, 也导致了边界层厚度无法进行精确修正;
(4) 更为棘手的问题是目前发展的CFD数值计算技术也难以对复杂高焓流动实现准确预测和评估, 同时, 目前发展的试验测量技术同样难以对其进行可靠性的验证. 这些研究手段方面的问题制约着高性能高焓喷管设计理论和方法的发展.
随着我国经济的快速发展和人们生活水平的不断提高,人们对生活质量的要求越来越高,越来越多的人涌进城市,使得我国的城市化水平不断提高。青岛市作为我国经济发展迅速的城市,同时作为美丽的海滨城市,其人口城市化率每年都在提高(见图1)。
医院人力资源管理包含众多内容,其中绩效评价管理和薪酬管理是其重要组成部分,而且这两项管理工作的内容都较为琐碎,对管理体系构建的科学性有较高要求。在新医改实施下,医院必须兼顾现阶段发展过程中经营效益和社会效益,努力改善医疗服务水平,为患者提供满意服务。绩效评价管理和薪酬管理是优化医院内部管理的重要手段,应在新医改要求下,对传统评价体系及薪酬体系中存在的问题作出有效整改。
3 高超声速喷管设计方法
比较3种设计方法获得的喷管长度, 第3种方法设计的喷管最短, 第2种最长. 第3种喷管在喉道附近膨胀过急, 轴向压力梯度大, 通常会引起壁面边界层厚度突变, 甚至产生流动分离现象.膨胀度过大导致喉道流动较为复杂, 不符合均匀声速来流的假设. 第2种方法采用较小的最大膨胀角, 通常设计的喷管长度过长. 对于高超声速流动, 较长的喷管会产生更厚的边界层. 因此, 比较而言, 第1种较为常用.
3.1 基本原理
风洞喷管几何型面分为轴对称、二维、三维和非对称等几种类型, 而高超声速喷管大多采用轴对称的型面结构. 根据喷管流动特征, 轴对称喷管设计一般分为4个区域: 亚声速收缩段、初始膨胀段、消波段和试验段, 如图2所示.
在高超声速喷管设计中, 为了保证喷管出口气流的平直均匀, 从喉道到出口采用扩张曲线,一般按照超声速MOC方法设计. 喷管扩张曲线分为前、后两段, 其分界点在B点处, 称为转折点或拐点. 如图2所示的OA线所在截面为喉道位置最小截面, 喷管曲线用ABC曲线表示,β为斜角,且 tanβB为 管壁曲线中B点 斜率, 且βB为最大膨胀角, 其大小取决于设计马赫数和设计方法.
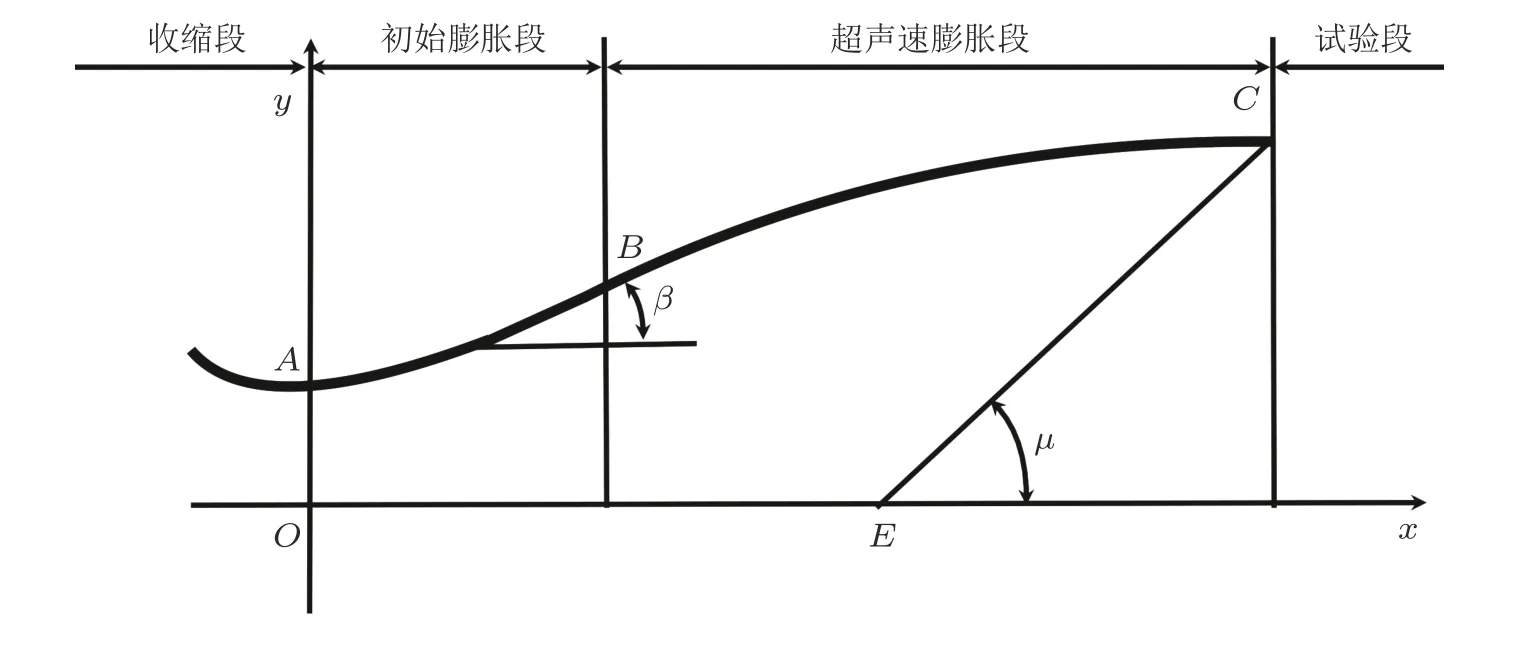
图2

式中,v1为 试验段马赫数对应的普兰特-迈耶角.AB轴向距离称为初始膨胀段长度, 段内气流膨胀加速, 气流方向沿着壁面AB曲线逐渐向外偏转. 气流膨胀过程中会产生一系列膨胀波, 持续到转折点B为 止. 从B到C称为消波段, 且BC曲线的斜率逐渐减小, 一直到C点变为零. 流动沿着BC曲线产生一系列压缩波, 以抵消前段产生的膨胀波, 逐步增大核心均匀区. 试验段对应的马赫角为µ1, 即直线EC与喷管轴线的夹角. 当气流达到EC线时, 气流完成了膨胀加速过程, 其流动方向与轴线平行, 达到设计马赫数.
在常规高超声速风洞喷管设计中, 一般给定风洞喷管出口尺寸, 然后根据面积比公式计算喉道尺寸, 实现设计马赫数. 面积比和马赫数存在如下关系

式中,A为喷管截面积;A∗为 喉道处截面积;r为从原点开始至任意点之间的距离;r∗为从原点开始至喉道断面间的距离;Ma为 喉道处的当地马赫数;γ为气体比热比, 理想气体为1.4. 由于没有考虑高温引起的比热比的变化, 该公式对于低总温高超声速风洞喷管设计是有效的. 对于高焓喷管型面设计, 人们仍然可以采用传统方法开展高超声速喷管设计, 但对于真实气体效应的影响需进行必要的修正处理. 本文后面将会详细讨论.
在特征线理论和方法的基础上, 早期学者发展了多种喷管设计的解析方法. 解析法的共同特点是假设在喷管转折点B处 (参见图2), 流动为超声速源流. 此时, 利用解析的方法, 计算得到B点之后的曲线, 这条曲线的设计原则是要消除所有在其线上反射的膨胀波. 对于B点前的型线, 处理方式不同, 但一个共同的思路是前段曲线应能够把喉道处的均匀声速来流变成转折点处的超声速源流.
(1) 假设喷管内的流动为理想流动, 根据等熵关系式设计势位势流型线 (无黏型线);
(2) 估算喷管壁面的边界层发展, 实际上就是估算边界层位移厚度;
(3) 将估算的边界层位移厚度在法向上叠加到位势流喷管型线.
此外, 本文讨论的喷管设计主要针对高超声速喷管的扩张段设计, 喷管收缩段的设计由于方法较为简单 (主要采用多项式拟合方法)且对超声速段的设计没有直接的影响, 在此不做赘述.
2.2.2 草原生态安全待评物元的确定 以2007,2010和2013年为代表实例,根据各评价指标的具体量值,天祝牧区2007、2010和2013年高寒草原生态安全评价的待判物元矩阵表示为R2007,R2010和R2013:
3.2 传统高速喷管设计方法
MOC方法的提出为现代喷管设计奠定了理论基础. 早期的超声速、高超声速风洞的喷管大多是基于特征线方法进行设计的, 而且应用的较为成功. 尽管高超声速风洞喷管流场出现了一些特殊问题, 诸如真实气体效应、喉道散热和变形、更厚的边界层发展等, 但是通过一些修正后也得到了相对满意的结果.
由MOC方法衍生出了多种理论方法, 包括图解法和解析法, 这些方法设计出的喷管型线基本上可以分为以下3种形式 (伍荣林等1985):
(1)设计弯曲喉道型线 (“曲率半径”较大), 采用最大膨胀角βB=0.5v1;
(2)实行重点施工环节的验收制度。如对二开固控设备、水平井下FEWD、进入沙河街组地层等特殊环节进行验收。
(2)设计弯曲喉道型线 (“曲率半径”较大), 采用最大膨胀角βB<0.5v1;
克莱默希望,在它们从人们的视线中消失之前,人们能够更好地认识到漂流木在河流和海洋生态中的重要作用,更好地理解河流、树木和海洋之间的关系。
近十几年来, 在国内外航空航天领域, 高超声速飞行技术得到了高度重视. 随着新一代空天飞行器的研发, 对高超声速风洞地面试验研究提出了更高要求, 尤其是对高焓试验来流的品质越来越关注, 凸显了发展高焓喷管设计理论和方法的重要性. 因此, 本文重点综述了传统高超声速喷管设计的主要理论和常用方法, 它们在高超声速喷管设计中一直发挥着重要作用.
采用传统MOC方法设计的喷管, 在高马赫数流动条件时, 边界层发展的厚度已不能再忽略处理 (尤其是现代喷管设计一般针对的风洞尺度都较大), 所以要进行适当边界层的修正才能满足出口设计马赫数要求. 本文还将对MOC局限性做进一步的分析和讨论.
3.2.1 图解设计法
在20世纪四五十年代, 一些学者针对喷管设计提出了多种图解方法. 其中, 典型的Busemann法 (Busemann 1931, Preiswerk 1940)是最基本的一种特征线网格法. Busemann假设喉道处的声速流动是均匀的, 依据喷管设计理论, 在转折点B以前, 根据经验任意给出一条斜率逐渐增大的初始曲线AB, 且在B点 处满足βB=0.5v1.
如图3, 以折线AA1A2···ANB代 替AB曲 线,Ai为转折点, 每一段折线向外转折相同 (或可变化)角度Δβ, Δβ取值越小越精确. 根据特征线理论, 所有发自Ai点的膨胀波、在喷管轴线或曲线壁面上的发射波、以及彼此相交后产生的波均可计算得到, 所有波线围成的区域都是均匀流区域. 最终, 依次连接折点Ai形成连续光滑喷管型线. 超音速气流绕外钝角流动产生的是膨胀波系,这种方法仅仅用一道单波代替, 是一种近似. 这种方法对于设计非常规喷管是有用的, 而对于常规高超声速喷管, 后来发展的解析法则更为方便, 计算结果也更精确.
(3)设计“急变”喉道型线 (“曲率半径”较小), 采用最大膨胀角βB=0.5v1.
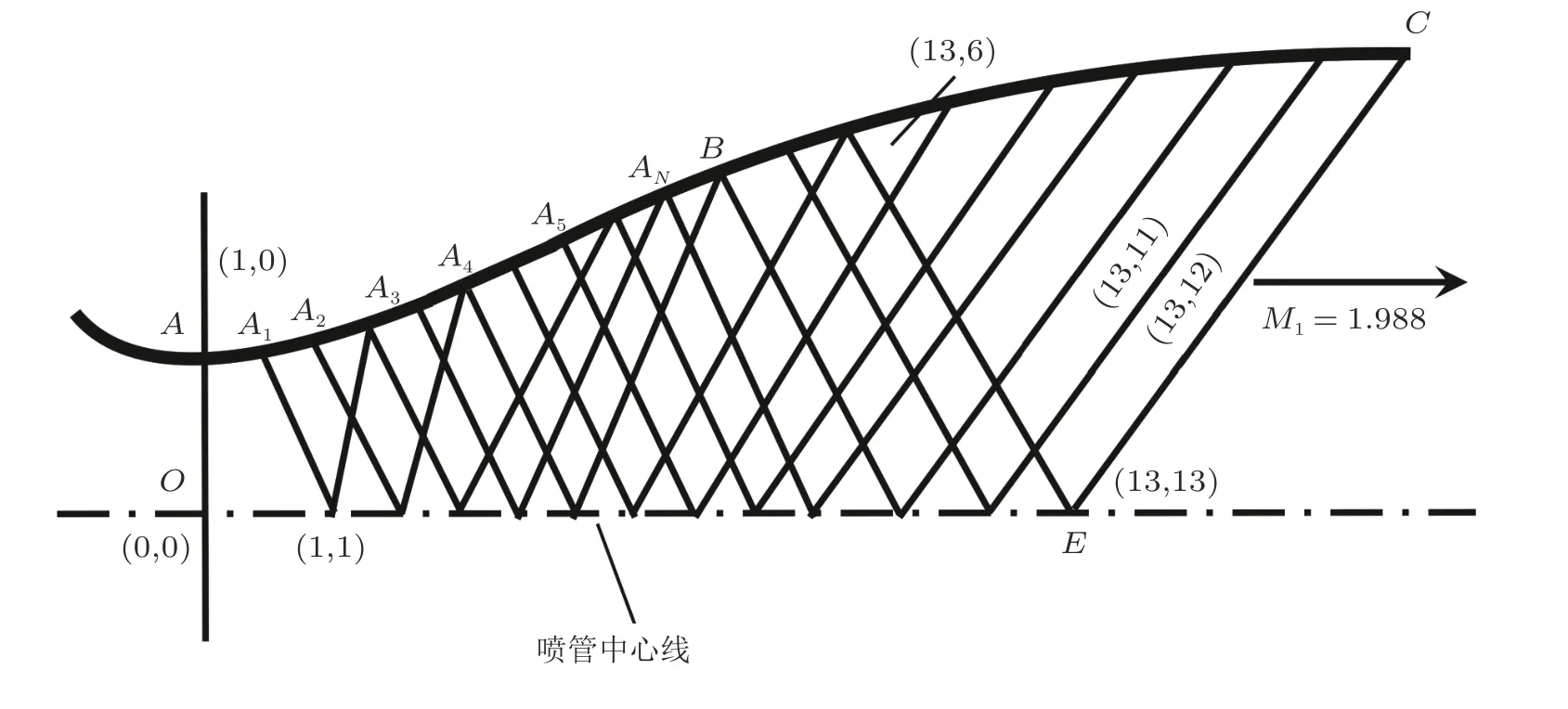
图3
Puckett (1946)改进了原始的Busemsmn方法, 新方法具有诸多优点. 首先, 使用简化的初始设计曲线, 使得设计喷管所需的时间或工作量减少大约一半. Puckett方法从喷管中间开始向两端进行特征线的计算, 并假定在最大膨胀部分 (拐点处)通过喷管的气流具有均匀的速度和均匀变化的流动方向 (如图4所示). 根据经验, 这些边界条件的设定是合理的. 利用这些边界值, 可以通过与原始Busemann相同的方法确定喷管的出口部分 (消波段). 以此类推也可以构造初始膨胀段. 此外, 如果β小 于βB, 则必须增加一个或多个转折点来反射膨胀波. 由于可以选择反射波, 所以可选择多个初始曲线AB, 在其对应的消波段型线实现指定的设计马赫数. 实际上, 如果网格尺寸可以无限小的话, 理论上有无限多个初始曲线可供选择. 同理, 对应特定的初始膨胀段曲线也有无数个消波段曲线可以使用. 但是, 尽管每个消波段曲线都有无数个合适的初始曲线, 这并不意味着任何满足面积比 (见式 (8))要求的喷管型线都是合适的. 此外, 对于大多数实际工程应用,只要适当加以修正处理, 一般可以忽略使用任意初始曲线引入的误差.

图4
在Busemann方法喷管设计中, 膨胀波是沿着平滑的初始曲线上某些点产生的. 也就是说, 膨胀波的间隔是有序的, 尽管它不需要是均匀分布的. 当使用的网格尺寸较大时, 有时膨胀波在某些点处从喷管壁面反射, 从而破坏后面膨胀波系间隔的有序性, 由此最终的喷管消波段型线会出现轻微的不规则性. 理论上随着网格变得无限密, 这些不规则现象便会消失. 但实际上Puckett方法无法避免这个问题, 所以在应用该方法的时候, 一般假设消波段曲线不受初始曲线的波形影响, 并通过加密网格来减小误差, 给出尽可能光滑的喷管型线. 但受到当时计算技术的限制, 网格加密后的计算量增大, 相应的设计效率降低. 同时, 随着解析法的提出和发展, 得到的喷管流场远优于图解法, 因此早期图解法基本不再应用于高速喷管的设计.
实验1加速比是衡量算法串行处理和并行处理效率的一项重要指标,本文计算了处理表1中不同大小数据集的加速比,实验使用单个节点的Hadoop集群即一个主节点和一个从节点的情况代替算法串行处理时间的近似值。由图7的结果可以看出,随着数据规模的逐渐扩大,算法的加速比性能越来越好。
3.2.2 解析近似设计法
依据图2中喷管型面结构, 解析法与图解法类似,B点为转折点 (或拐点), 型线ABC在B点有最大的斜率,AB段 和BC段分别为初始膨胀段和消波段.A和C点为喷管型线的起始点和终止点,通常喷管型线在这两点的斜率为零. 此类方法一般采用源流假设, 初始膨胀段设计原则是采用不同的近似方法, 将喉道处的声速来流变成转折点B处的源流. 消波段型线则是把超声速或高超声速源流变成满足设计马赫数要求、流向与轴向平行的均匀来流, 同时要能消除喷管壁面所有的膨胀波.
依据上述设计理论介绍, 传统的喷管设计可分为3个步骤:
在喷管型线设计中, 首先要根据严谨的理论方法设计出不考虑黏性的无黏位流型线, 然后进行边界层的修正. 但其中一个很大的问题是对边界层的评估、计算很难做到足够精确. 尤其对于高超声速和高焓流动边界层, 理论方法和数值方法都很难准确评估. 因此, 十分精确的喷管位流型线设计则显得完全没有必要. 此外, 理论计算出的波系可能完全不同于实际的流动情况. 基于此, 到目前为止, 大部分的喷管位流型线均采用简单近似的方法进行设计, 这大大减少了设计工作量.
引言:合理有效的护理对于患者的恢复以及生活质量的提升都十分重要。双肺移植患者对于呼吸机的依赖性不言而喻,而在呼吸机使用过程始末的护理手段与措施也直接影响到患者的体验。如何加强在撤机前的患者适应性训练,如何做好撤机过程中的保障措施,如何在撤机后为患者营造一个舒适的环境并提供充足的呼吸道管理以及营养保证。这些都是摆在护理工作从业者面前的现实问题。
此外, 解析法源流假设的思想对于早期不考虑高温效应影响的喷管设计 (尤其是低速喷管)在某种程度上是合理的, 设计结果基本满足使用要求. 对于较高马赫数喷管的设计, 为了得到更高品质的流场则不得不应用各种优化技术进行设计后处理. 本文回顾并对比了喷管设计中一些较为经典的解析法, 有些方法至今依然有应用, 由此可以把握喷管设计方法的发展脉络.
3.2.2.1Foelsch法
683 Therapeutic effect of pingyangmycin injection combined with hypercator resection under suspension laryngoscope on laryngopharyngeal hemangioma
Foelsch (1946, 1949)提出了一种近似方法(图5). Foelsch方法假设喷管某一区域为源流,采用经验公式设计初始膨胀段, 并利用特征线法过渡到均匀区. 由于源流假设的局限性, 这种方法设计的喷管一般很长, 而且源流区与均匀区直接相接造成轴向速度梯度不连续, 影响了流场品质. Foelsch法并没有从理论上确定一条曲线并保证在转折点处满足源流假设条件, 而是采用了一条经验曲线. 该曲率单调变化且在B点处满足面积比公式的要求, 曲线方程如下
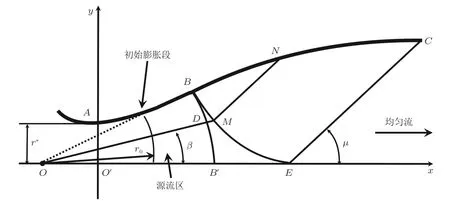
图5

式中

由该方法得到的初始段型线在转折点处的实际流动与源流有差别, 并对试验段流场均匀性产生一定影响. 另外, 其消波段型线的设计在首尾两端点(B和C点)的曲率不连续.
Crown (1948)对Foelsch法进行了改进, 给出了一条新的曲线 (见式 (11))作为初始膨胀段型线. 但总体而言, 并没有对Foelsch方法在本质上有很大的改进
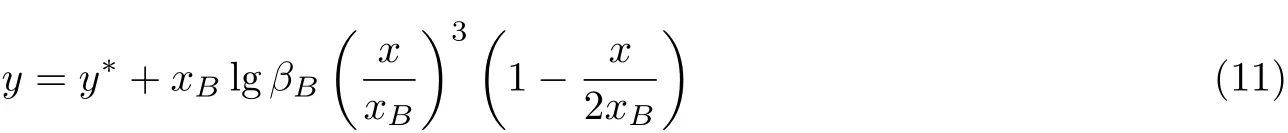
式中
1.2 农村地区信息贫困的归因研究 何隽等[15]对贵州农村信息贫困调查研究,赵奇钊等[11]对武陵山片区信息化发展水平评价与信息贫困研究,张孟嘉[16]对安徽农村信息环境调研及分析,孙贵珍等[17]对河北城乡信息化相关因素比较研究,李玉华[18]对吉林省农村信息贫困因素分析,唐乐融[19]和李钢等[9]分别对河南省鹤壁市淇滨区、洛宁县和栾川县农村信息状况进行调查报告,通过对上述文献进行归纳总结,发现这些研究者都将信息贫困与我国的农村地区联系起来研究,重点研究农民这一信息贫困群体,他们归结出信息贫困主要有以下形成原因。

Foelsch法的贡献和意义是用源流假设对喷管喉道附近流场进行了“合理”处理, 使喷管设计中最为复杂的喉道区域的壁面型线设计得到大大简化. 也由此, 衍生出了一系列基于源流假设的喷管设计方法, 这些方法被应用于20世纪建造的大部分高、低速风洞的喷管设计当中.
3.2.2.2圆弧加直线方法
取已知氯霉素浓度的蜂农蜂蜜15 g向其中添加浓度分别为130、260、660 μg/kg的氯霉素溶液各2 ml进行加标回收实验,按1.3.3第二种方法进行样品前处理,按1.3.2中V(甲醇)∶V(水)(0.2%磷酸氢二铵缓冲液,pH值5)=40∶60的色谱条件进行实验。每个加标水平重复3次。氯霉素回收率结果见表2。其回收率为84%~93%,相对标准偏差4.2%,满足线性分析要求。
Cresci方法在初始膨胀段AB的 设计采用了Foelsch方法的经验曲线, 在消波区域BDEF内假设轴向的速度分布满足一个多项式. 根据经验,D点马赫数选择比E点马赫数小0.2,E点马赫数即为设计马赫数. 此时, 如果假设DE段速度分布满足一个三次多项式

图6
圆弧可使喉道处的超声速流动向源流过渡, 直线段则有利于流动变成源流, 而且越长越能使流动接近真正的源流. 易仕和等(2013)对采用圆弧加直线方法设计的超声速喷管型线进行了计算分析, 认为该方法的源流假设并不是很合适, 而且直线段的膨胀取决于圆弧膨胀段发出的膨胀波的反射, 相应的膨胀效率较低. 圆弧加直线的方法与Foelsch法都是以假定转折点处能否得到源流为基础的, 不同的只是初始膨胀段型线设计方式不同. 关于消波段型线的设计, 两者完全一样. 此外, 两种方法设计的喷管均会导致轴线上的速度梯度间断, 因而也导致了喷管型线曲率的不连续. 关于圆弧加直线的详细设计方法和公式, 可参阅易仕和等(2013)和伍荣林等(1985)的著作.
3.2.2.3Cresci法
所有患者均仰卧于体部的真空垫进行CT定位扫描及接受射波刀(Accuray Incorporated, Sunnyvale, CA))放射治疗。肿瘤靶区(gross tumor volume, GTV)定义为影像学所示病灶靶区,计划靶区(planning target volume, PTV)定义为肿瘤靶区在x、y、z轴方向各外放2~3 mm。总剂量30~36 Gy(5~8次分割)。至少90% PTV被处方剂量线包绕。
Cresci (1958)通过在型面中设置一个部分消波区对Foelsch系列方法进行了改进, 尝试解决Foelsch法和圆弧加直线方法的算法导致轴向速度梯度间断问题. Cresci方法是把喷管流场分成3个区域 (图7): 第1区域 (即图中OABD区域)为喉道膨胀区, 认为是从原点发出的源流; 第2区域 (即图中BDEC区)为过渡区, 该区将源流整流, 矫直成平行流; 第3区域 (即图中均匀流区)为平行流区, 气流具有同样马赫数的平行均匀流.
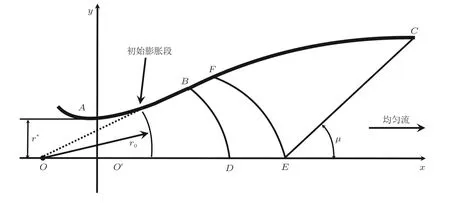
图7
圆弧加直线方法是一种经验性的近似方法, 其初始段曲线用圆弧加直线组成. 圆心位于通过喉道的y轴 上, 而直线的斜率为 tanβB. 圆弧与直线相切于P点, 见图6.

由于气体黏性效应, 实际喷管流场不同于无黏流场. 黏性影响表现为: (1) 喷管壁附近流场出现附面层, 其厚度沿喷管壁的发展影响了喷管主流区流动; (2) 喷管内波系与附面层发生相互干扰, 不但影响了边界层内的流动, 而且改变了喷管壁上的波系的发生和反射, 从而不能实现位势流设计中完全消除膨胀波反射的要求. 如果喷管型面直接采用位势流设计的型面坐标, 那么实际的喷管流场将会出现两个问题. 一是由于壁面存在黏性边界层并且厚度不断增加, 因此改变了波系形状, 使得到达喷管出口的流场不均匀; 二是较厚的边界层减小了有效位势流面积, 因而改变了面积比, 使喷管出口的实际马赫数低于设计马赫数. 这两个问题在高超声速喷管流动中更为严重, 尤其是高焓喷管流动. 因此, 必须对设计完成的位流型线进行边界层修正. 考虑喷管附面层修正时, 一般是考虑修正附面层对喷管流量的影响. 具体方法是计算喷管位势流型线各个点位置的边界层位移厚度, 然后在法向方向叠加到位流型线上, 即将理论型线向外推移, 其推移距离等于边界层位移厚度. 对于低速喷管, 其位移厚度较小, 通常也可以在垂直轴线方向上取位移厚度.


并且由
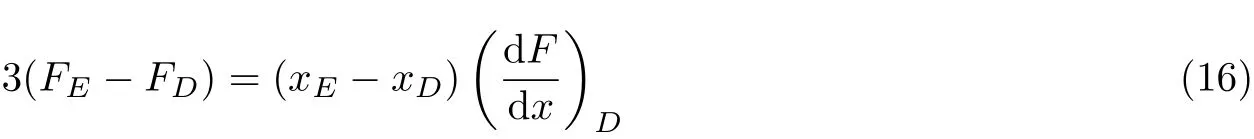
选定xE的 值, 将边界条件代入三次多项式, 可以确定D点 和E点位置. 通过E点左行特征线为直线且其马赫数为设计马赫数, 因此特征线端点C可以确定. 将BD,DE,EC作为边界条件, 利用特征线理论和质量守恒定律可以求出整个流域的特征线网格以及BC段喷管型面曲线. 在初始膨胀段设计中, 仍然采用Foelsch方法的经验曲线, 由此设计的喷管型线很难再进行优化. 但是, 相比Foelsch法, Cresci方法在喷管型线设计中已经是较为成熟的技术了.
3.2.2.4Sivells法
采用上述设计方法进行喷管设计时, 只考虑喷管型面问题, 因此也很容易造成喷管轴线上扰动聚集和壁面流动分离等现象. 20世纪60年代末到70年代, Sivells (1969, 1970, 1978)在Cresci设计思想的基础上, 考虑Hall跨声速理论 (Hall 1962), 提出了基于轴向速度与马赫数分布的喷管设计方法. Sivells法通过设置轴向马赫数分布得到了具有连续曲率的喷管型线, 使得喷管内部没有集中的压缩波, 出口马赫数分布均匀, 大大改善了流场品质.
Sivells方法通过已知边界点, 设定的轴向马赫数分布以及近似的声速喉道解析解三者之间的特征线网格来确定喷管设计型线. 如图8所示, 喷管分为3个区域,TIEG所组成的喉道区,GEBA所 组成的径向区,ABCD所 组成的下游区. 对于径向流区, 特征线EG和AB之间的区域都是源流, 而且从G到A点 的型面是与轴线成ω角的直线. 因此, 确定型面主要有两部分工作, 也就是要求解两组特征线方程. 一是确定分支线上H点到G点 的喉道型面, 其中H位于从声速点I出发的左行特征线上, 采用Hall的跨声速流动方法计算喉道区域的流场; 另一个是确定从A到喷管理论端点D的下游型面.图8中特征线CD是 直线并且D点为理论上喷管型线终点, 即喷管出口位置. 根据这些假设的边界条件, 利用特征线网格结合质量守恒定律即可求解IHGE和BADC区域的流场, 从而得到沿着HG和AD的 喷管型线.TH段 型线由跨声速解得到, 求解流程是先假定从I到C点的速度分布, 即其喉道的理论跨音速条件, 然后使得中间区域的源流条件以及喷管出口设计流动条件相配合.I到C的轴向速度分布分为三步处理: 一是从喉道区域中音速点I到假定径向流开始点E, 这部分速度分布是由一个4次多项式来描述; 二是从E到径向流结束点B, 这部分速度分布由产生径向流条件给出; 三是从B点到均匀流开始点C, 这部分马赫数分布由一个5次多项式来描述. 其中多项式系数的选择原则是轴向速度的二阶导数处处连续, 且在C点处导数为零. Sivells方法的详细求解过程和喷管设计流程可参考Sivells (1959, 1970, 1978)著作.
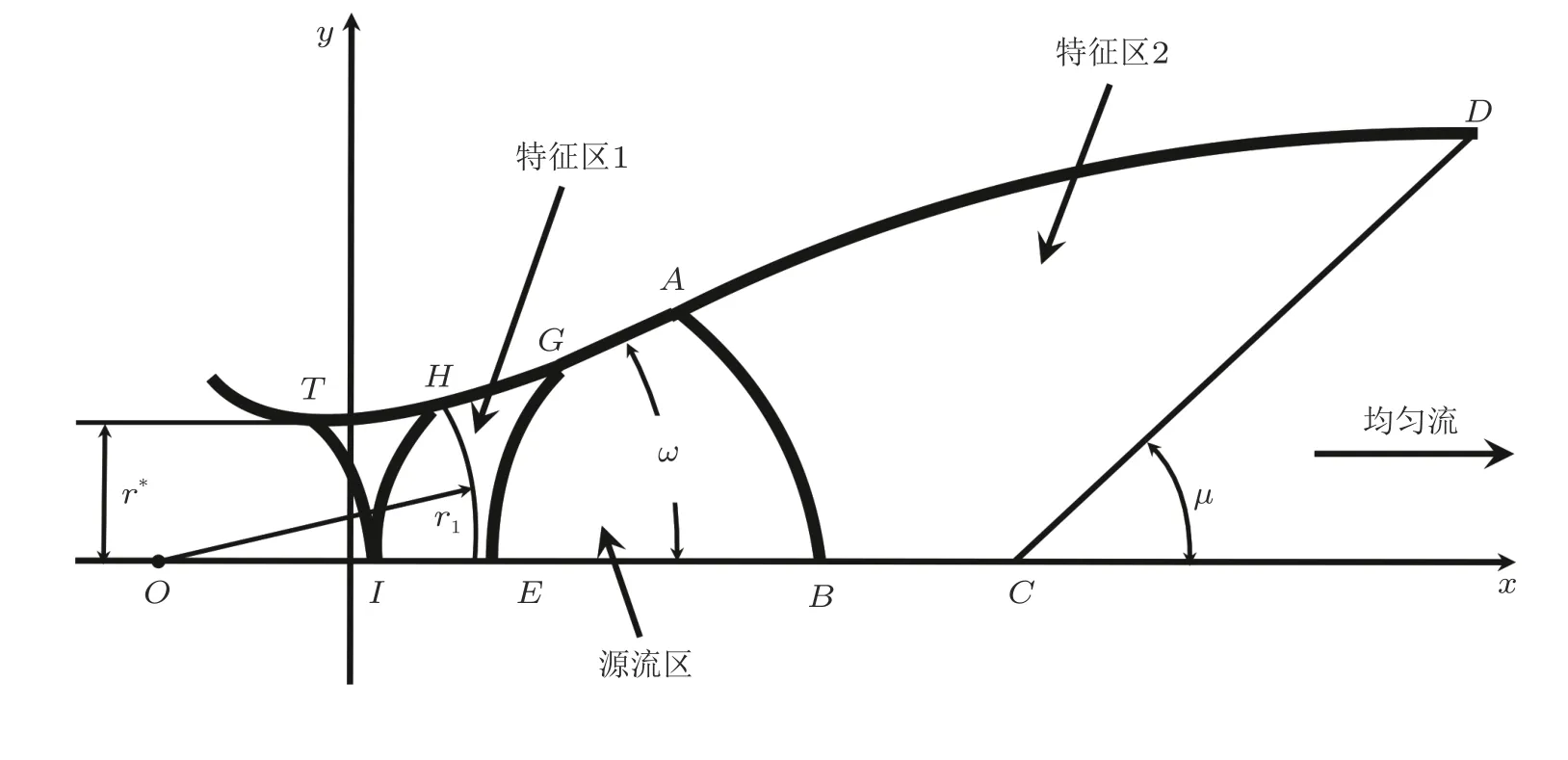
图8
Potter和Carden (1968)使用传统MOC方法设计了AEDC-VKF (Arnold Engineering Development Center, von Kármán Facility)低密度高超声速风洞的Ma=9, 10两套喷管, 其无黏位势流型线设计则是采用了Cresci (1958)和Sivells (1963)相结合的设计方法. 设计思路如图9所示, 在消波区 (III区)采用了基于源流假设的Cresci的方法, 在轴线上按照Sivells的设计流程给出马赫数分布曲线完成型线的设计. 实验结果表明设计马赫数为9和10的喷管通过试验测量的喷管出口实际马赫数分别为10.15和9.30. 原因是该设计未考虑比热容比的变化影响, 且由于密度较低而认为喷管流动为全层流, 因此带来了一定的设计误差.
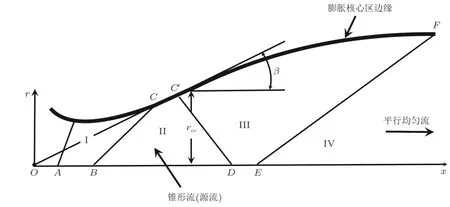
图9
易仕和等(2013)对采用Sivells法设计的马赫数为6和7的高超声速轴对称喷管进行了流场数值分析, 发现通过圆弧加直线、Foelsch和Cresci等喷管设计方法的对比, 发现Sivells方法设计的喷管流场品质相对更好, 而且随着马赫数的增加, 能够进一步改善流场品质, 因此Sivells法更适合于高超声速喷管的设计. 从某种程度上讲, Sivells方法在喷管设计理论与方法的发展中具有里程碑意义, 它基于传统特征线方法, 经过不断完善, 使得喷管设计理论与方法趋于成熟. 到目前为止, Sivells法是国外公认的精度较高, 并且得到广泛工程应用的高速喷管设计方法之一.
3.2.2.5Sivells衍生方法
Sivells方法提出时, 受到当时计算技术的发展限制, 设计喷管的长度较长, 尤其是高速喷管.针对该问题, 诸多学者提出了一些喷管短化设计方法, 比较常用的是采用喉道直声速线和弯曲声速线假设的喷管短化设计方法 (Ali et al. 2012). 但是, 这些喷管短化方法可以满足较低马赫数的设计要求, 在马赫数较高时却很难保证流场品质. 为了解决高超声速喷管设计过长的问题, 张敏莉等(2007)提出了一种新的短化喷管的设计方法. 该方法保留了Sivells方法, 通过设置轴向马赫数分布来计算喷管型线. 设计思想舍弃了源流假设, 利用六次贝塞尔 (Bézier)曲线来构造轴向马赫数分布, 并结合Hall的跨声速理论设计喷管型线. 该方法取消了传统方法的一元跨声速流和源流假设, 摆脱了经验公式的束缚. 采用六次贝塞尔曲线构造的轴向马赫数分布可以灵活控制, 二阶导数在全场连续, 这将保证喷管内部参数不会发生突变, 从根本上杜绝了产生集中膨胀和压缩波的可能. 因此可以通过设计参数的选择使喷管达到短化、优化的目的.图10给出了喷管短化和优化的对比结果.

图10
图11是张敏莉等(2007)给出的Sivells方法和新的短化方法设计结果比较, 校测得到的出口流场与数值模拟的结果符合得较好, 验证了设计方法的合理性以及数值模拟结果的可靠. 但张的工作仅仅针对Ma=3.5的工况进行了喷管设计, 而且在低马赫数条件下, 新的喷管短化设计方法并没有比传统Sivells方法具有十分明显的优势. 随后, 赵一龙等 (2012) 采用B样条曲线构造轴线上速度分布以避免轴向马赫数分布出现大于喷管出口马赫数的问题, 取得了较为理想的效果, 但是仍然针对的是低马赫数的喷管设计分析, 给出的算例为超声速Ma=4的情况.
Tajfar等(1991)利用源流面积比和马赫数的关系, 采用三次或五次多项式描述面积比分布,然后根据面积比反算马赫数分布. 采用了带有面积比的多项式后, 轴线马赫数不会超过设计出口马赫数, 但仍可能产生分布不合理的现象, 特别是在起点附近存在马赫数增长过快的可能性, 进而导致计算特征线网时特征线相交. 胡振震等(2016)在Tajfar等(1991)研究工作基础上, 改进了基于面积比的轴线马赫数分布预设方法, 提出了一种多点控制的轴线特征点分布方法, 并应用于马赫数12喷管的型线设计. 他们采用数值计算对比分析了基于Sivells轴线马赫数分布、基于B样条曲线马赫数分布、基于面积比三次及五次多项式分布等4种预设马赫数分布设计的Ma=12喷管流场. 研究结果如图12所示, 他们分析的结论是, 4种不同轴线马赫数分布的设计流场与数值模拟结果基本一致. 实际上特征线方法计算的出口参数就是设计出口马赫数, 只要数值过程足够精确, 理论上特征线方法得到的型面应该就是能够产生均匀出口马赫数的型面. 然而, 由于计算过程中, 布点数、网格和数值方法等都带来误差, 所以实际得到的喷管出口必然有一定的偏差, 而这个偏差需要用数值模拟方法进行评估.
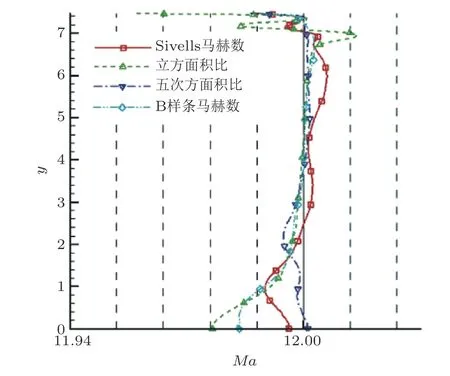
图12
理论上讲, 对于不存在明显高温气体效应的高超声速喷管, 采用MOC方法设计的喷管无黏位势流型线基本可以达到要求, 并且采用不同改进方法可以进一步满足喷管设计当中所关注的其他特殊要求. 到目前为止, 起源于MOC最成功的改进方法为Sivells喷管设计法, 尤其对高超声速喷管的设计, 得到了广泛认可并沿用至今.
3.3 边界层修正的理论方法
喷管壁面边界层厚度引起的喷管横截面的改变, 可用位移厚度δ*分布表示.图13所示的位移厚度定义为
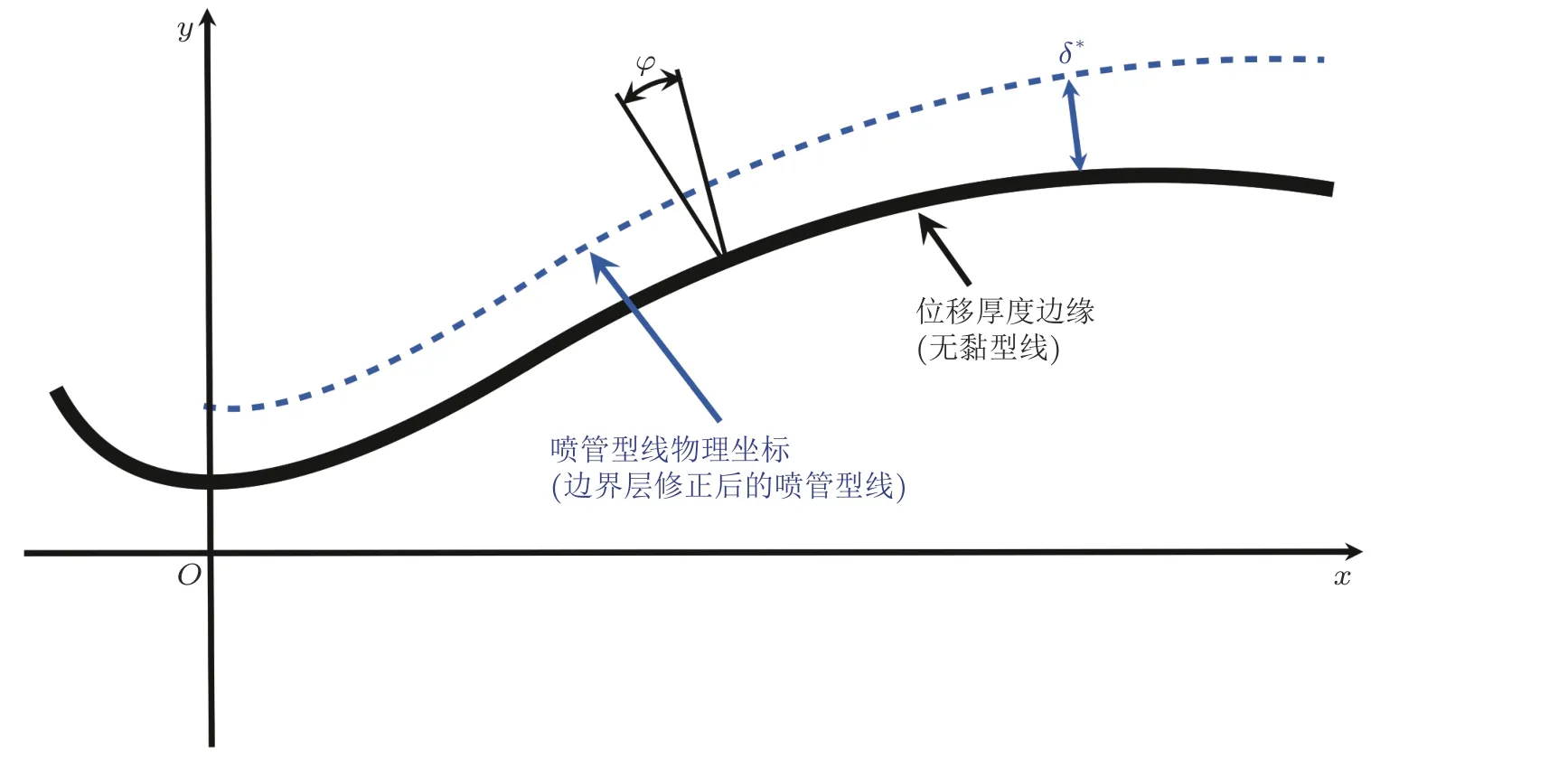
图13

式中,ρ1和u1为 边界层边界处的密度和速度. 把喷管位流型面沿壁面法向向外排移δ∗厚度, 即在位流型线法向叠加δ∗厚度. 喷管的边界层修正通常是在喷管的型面壁上按照以下公式进行修正

式中,x位流和y位流为 位流型线坐标;θ为 位流壁面对x轴的倾斜角度. 喷管壁面上的增长规律与黏性流动的特点有关, 喷管内气流沿轴向加速时, 壁面上边界层一般处于顺压力梯度. 边界层厚度的分布可以用理论方法、经验方法和数值方法来确定. 在低速风洞喷管设计中, 对其边界层位移厚度的计算和评估较为粗略, 通常采用理论近似或经验公式. 由于喷管较短, 其边界层较薄, 这种简单的修正方法不会在喷管出口引起很大的设计偏差, 通常都能得到相当满意的结果. 对于高超声速风洞, 由于喷管长度较长, 边界层较厚, 采用理论和经验公式的边界层修正所带来的误差不可忽略, 尤其是对于高焓喷管设计. 所以, 无论采用哪种方法, 边界层修正的效果实际上取决于对边界层厚度的准确评估.
高超声速风洞喷管壁面边界层 (低密度风洞除外)还有可能发展为湍流边界层. 对于常规高超声速风洞, 为了防止空气组分液化, 一般需要将试验气体加热到几百开. 所以, 风洞壁面上的热传导使得喷管流场的计算变得更复杂 (孙启志 2005). 高焓气流边界层计算方法目前仍不太成熟,大多数是直接把低速湍流边界层计算方法移植到高超声速边界层计算. 应用比较多的是Sivells-Payne方法 (Sivells & Panye 1959), 其计算相对比较简单, 但没有考虑真实气体效应对边界层发展的影响. Preiswerk (1940)提出了Persh-Lee方法, 该方法以轴对称动量方程为基础, 且考虑了高温气体效应的问题.
总体来看, 边界层修正方法是采用不同计算模拟方法对边界层厚度进行计算, 获得位移厚度,然后对之前设计完成的位势流型线进行修正处理, 也称之为MOC/BL (the method of characteristics/boundary-layer).
3.4 特征线方法的局限性
基于特征线理论的解析方法是喷管设计方法发展的主流, 针对理想气体高超声速喷管的型线设计, 从20世纪40年代末至今已经发展得较为完善. 自20世纪80年代起, 随着CFD计算技术的发展, 采用特征线无黏位流型线设计结合边界层修正的方法 (MOC/BL)获得成功, 其设计流场结果得到了CFD数值计算的验证和评估 (Benton 1989). Benton (1990) 详细分析了传统MOC方法应用到轴对称高超声速喷管设计中的局限性问题, 认为经典的特征线法结合边界层求解进行位移厚度修正 (MOC/BL)的喷管设计方法对于高超声速喷管的设计也存在可靠性问题.MOC/BL方法对于马赫数小于8的喷管相当有效, 但是随着流动马赫数增大, 尤其是对于超高速高焓流动模拟存在局限性. 这种情况下, 相对于流场均匀区直径, 边界层变得很厚, 基于MOC/BL方法设计的喷管难以达到设计要求. Benton (1989)对马赫数为13.5和17两套MOC/BL设计的喷管采用Navier-Stokes (N-S)方程进行求解, CFD结果与设计要求的一致性较差. 进一步考虑比热比影响后也没有改善数值结果. 所以, 当设计喷管所产生的流场品质不理想或者马赫数分布不符合设计参数时, 很大程度上是薄边界层假设带来的问题. Benton分析过的高超声速喷管流场中都存在压缩波, 这些波发生在拐点附近, 带来来流场的不均匀性. 他建议开发一种使用抛物型Navier-Stokes (PNS)方程的设计方法, 解决边界层计算的不确定性问题. Candler和Perkins(1991)对高超声速边界层内的特征线反射进行了分析, 发现MOC/BL方法基本假设的层流边界层和喷管核心流是不耦合的. 如果边界层较薄、几何形状较短的低马赫数喷管, 该假设是一个合理的近似, 并且流动特征线反射位置基本在无黏型线上. 然而, 通过较厚边界层后, 实际的反射特征线与通过位势流边界反射的计算特征线之间存在一定滞后性, 即实际的特征线反射可能发生在较厚的边界层内部而不是发生在位流边界线, 导致实际反射特征线滞后于设计反射特征线, 最终使得传统方法设计的喷管流场品质下降 (Craddock 2000, Chan et al. 2018), 见图14. 因此使用经典MOC/BL设计的喷管存在流动特征线反射的偏差, 使得喷管消波段中的膨胀波未完全消除, 从而导致喷管出口流场不均匀. Benton (1990)认为使用MOC/BL方法设计的高超声速喷管,在马赫数约为7时就开始显示出边界层厚度影响, 这时湍流边界层增长到喷管出口, 其边界层厚度占喷管半径的百分比随着马赫数提高而增大. 因此, 需要发展更为精确的喷管设计方法, 该方法应能对边界层发展提供较为精确的评估, 使得边界层修正更加适当.

图14
3.5 基于CFD的分析设计方法
为了克服MOC/BL方法在高超声速喷管设计中存在的局限性问题, 20世纪90年代初期,Korte等(1992a, 1992b, 1992c, 1992d, 1993, 1994, 1995)提出了基于CFD数值技术的高超声速喷管设计方法, 其设计优化流程见图15. Korte方法利用高精度CFD求解器 (Korte 1991), 耦合了基于最小二乘法的优化算法 (Huddleston 1989), 优化生成使喷管流向角度和出口马赫数变化最小的喷管型线. 其中, CFD技术求解了一套PNS方程, 可以对MOC/BL方法设计的喷管出口流场进行优化处理. Shope (2006)将此方法称为“分析设计”方法. Korte方法的主要优点是采用了NS方程的求解器, 从而可以较准确处理高马赫数喷管的核心流场 (无黏流场)和边界层之间的相互作用. 在设计流程中, 将喷管流场CFD计算方法和喷管型线代入优化算法进行迭代计算, 直到获得均匀的喷管出口流场. Korte设计方法的精度取决于CFD求解器的精度以及优化算法所能达到最优解的性能. 另外, 该设计方法通过简单地采用三维流场求解器, 不仅可以设计轴对称喷管, 还可以设计三维喷管.

图15
Korte (1992c, 1993)对基于CFD方法的高超声速喷管设计方法进行了改进. 改进后的方法仅仅使用CFD计算技术即可完成整套设计流程, 无需利用MOC/BL设计的初始喷管型线. 在设计流程中, 轴线马赫数分布根据出口马赫数和流向角等参数进行了优化, 其中轴线马赫数分布仍然采用Sivells方法 (Sivells 1970). Korte方法基本上摆脱了传统MOC方法的束缚, 并且设计得到的喷管流场比理论方法更加精确. 显然这种基于CFD计算技术的设计方法对数值模拟精度的依赖性是很强的, 所以对于具有化学反应非平衡流动现象的高焓喷管, 也有待于进一步的探索. 本文后面还将详细讨论真实气体效应问题的处理方法.
2000年, Korte (2000)开发了一套计算代码, 使用Sivells的特征线方法 (MOC) (Sivells 1970)来处理高温气体流动, 且比热比可以随温度变化. Gaffney (2006)将该方法应用于设计HYPULSE激波/膨胀风洞的喷管. HYPULSE风洞为美国NASA兰利研究中心的高焓地面试验设备, 具有非均匀流场的喷管, 可以产生Ma=15的飞行焓值条件流场能. 计算代码利用MOC方法结合Euler方程组的求解, 其优点是不受现有代码结构 (或编程语言)的限制, 不必逐行处理、修改程序, 运行起来相对较快, 并且描述喷管型线的点数也基本取决于指定的初始点数量. Gaffney的方法未直接考虑黏性效应问题, 最终的喷管型线边界层修正可以通过采用N-S方程解 (Gaffney &Korte 2004) (通常只有一两次迭代)迭代耦合MOC解来完成.
Korte方法理论上允许在设计过程中使用任意CFD求解器和优化算法的组合. 一些学者(Keeling 1993, Tolle 1997, Shope 2006, Chan et al. 2018)在Korte方法基础上做了一些改进, 包括采用不同CFD求解器和优化算法. 在改进早期的Korte方法中, Korte开发了喷管设计的程序CAN-DO (Korte 1992d), 该程序在喷管型线设计中采用三次样条插值, 并通过调整样条插值点以寻求最优出口流场, 对喷管流场的分析采用PNS求解器. 近几年, Chan等(2018)采用一套开源雷诺平均Navier-Stokes (RANS)CFD求解器, Eilmer (Gollan & Jacobs 2013), 与单纯形优化方法(Nelder & Mead 1965)的结合, 用于喷管型线设计, 优化目标为在喷管出口得到具有最小流向角和最小偏差设计马赫数的流场. Chan等(2018)应用该程序设计了澳大利亚昆士兰大学激波风洞T4 (Hannemann et al. 2016)的喷管 (Ma=4, 7, 10), 并进行了数值和试验结果对比分析. 研究结果表明其核心区来流具有很好的均匀性, 喷管出口处马赫数变化小于0.5%, 流向角度变化小于 0.05°, 静态温度和流速变化均小于1%, 皮托管和静压力变化小于2%. 此外, 实验测量了3个优化喷管出口下游几个截面上的皮托压力, 与CFD数值模拟吻合较好, 证明了所提出的基于CFD的喷管分析设计方法的有效性.图16和图17为Chan等(2018)针对Ma=7喷管的优化结果, 并对比分析了网格影响和MOC方法的设计结果.

图16

图17
在高超声速喷管的设计中, 基于CFD计算技术的设计分析方法取得了较好的效果, 但设计流程较为繁琐. 尤其采用CFD计算技术耦合优化算法的设计过程, 其采用不同N-S求解器, 需要选取合适的优化算法, 因此不便于工程领域的推广应用. 唐蓓等(2019)采用基于CFD计算技术的MOC设计方法, 优化了一系列高超声速喷管设计(图18). 与Korte、Gaffney的方法不同的是, 该方法没有采用耦合到N-S求解器的优化算法进行优化处理高超声速喷管型线, 而是基于Sivells的无旋特征线方法, 通过求解高温化学反应非平衡流动的N-S方程组, 同时对喷管无黏型线 (位流型线)和高温边界层进行修正和优化. CFD求解器与MOC方法分别独立求解, 然后组合优化处理, 完成喷管型线设计流程, 使得设计方法变得简单并且方便使用. 利用每一迭代步的CFD数值流场解, 得出边界层位移厚度数据, 作为下一迭代步的边界层修正依据. 同时, 每一迭代步的边界层流场信息, 也将应用到下一迭代步的优化计算中. 其中, MOC方法的所有的初始条件和边界条件均来自CFD计算的喷管流场数据. 一般通过2 ~ 3次迭代即能得到较为满意的喷管出口流场. 对喷管流场是否达到设计要求的评估则是考察喷管出口核心区域流场流向角大小和马赫数分布的均匀性是否满足试验条件.
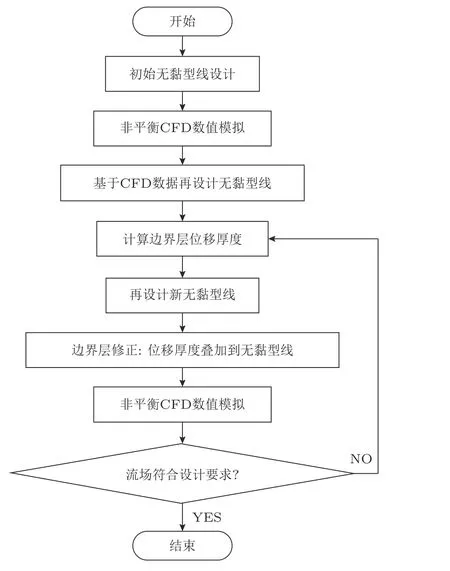
图18
总结来说, 基于CFD计算技术的喷管分析设计方法大致分为两类, 一类是CFD数值求解器与优化算法深度耦合设计方法, 即CFD分析设计方法(computational fluid dynamics/optimization method, CFD/OM). 该方法试图摆脱MOC解析设计方法或仅采用MOC设计型线作为初始输入条件. 相比于MOC/BL的理论解析设计方法, CFD/OM方法在优化过程中考虑了黏性效应的影响, 不必再进行边界层修正. 该方法可以得到更均匀的喷管核心流, 流场品质得到了一定提高, 尤其是针对边界层更厚、马赫数更高的情况. 但是, 该方法受优化过程中使用的控制点数量的限制, 并且相比MOC/BL方法, 计算成本非常高. 其次, 对每个要考虑的特定情况, 必须要重新修改代码, 使其应用具有诸多不便. 另外, 该方法设计结果精度完全取决于CFD计算格式和优化算法的精度. 因此, 对于超高速高焓流动, 会产生复杂的热化学反应和非平衡现象, CFD数值模拟的能力受到挑战, 其喷管设计优化方法的有效性需要根据实际测量进行评估. 另一类为CFD求解器、传统MOC解析方法、型线优化结合的设计方法, 简称为CFD/MOC/OM. 该类方法实现CFD数值计算与成熟的MOC设计方法独立求解, 然后组合优化喷管型线, 降低了设计流程中的技术难度, 也降低了计算量. 针对高焓喷管设计方面, 本文重点介绍CFD/MOC/OM方法.
4 高焓喷管设计方法
4.1 喷管设计中的真实气体效应问题
在20世纪50 ~ 70年代间, 出现了一系列关于理想气体超声速和高超声速喷管设计方法的研究报告 (Armstrong & Smith 1951, Ruptash 1952, Beckwith & Moore 1995, Johnson 1963)和著作(Lukasiewicz 1973, Zucrow & Hoffman 1997, Shapiro 1953). 他们提出的方法选取喷管半径为特征长度, 边界层厚度相对是可以忽略的小量, 喷管流场可以被作为无黏情况来处理. 一旦喷管位势流型线确定后, 再通过估算一个边界层位移厚度进行边界层修正即可完成喷管型线的设计. 对较低马赫数条件下高超声速喷管, 这些传统设计方法得到的结果还是可以接受的. 但是, 随着马赫数、总温、焓值的提高, 真实气体效应所带来的影响越来越明显. 在一个大气压力条件下, 当总温超过800 K时, 空气分子振动能被激发, 气体的比热比不再是常数. 温度达到2000 K时, 氧气开始解离; 超过4 000 K时, 氧气基本完全分解为氧原子, 同时, 氮气开始分解为氮原子. 对于高温、高压气体流动, 如果继续使用理想气体假设来处理喷管设计问题, 将会导致较大的误差, 传统的优化方法也不再有效.
比热比γ反映的是气体温度变化时, 焓值与内能变化之比. 空气在常温、常压下,γ=1.4. 只要温度和压力变化不大, 空气可以认为是理想气体时,γ则保持不变. 但在高超声速高焓条件下,喷管型面设计应考虑比热比变化对其产生的影响. 在早期的高焓喷管设计研究中, 主要考虑了由于温度和压力变化引起的气体比热比变化对喷管型线设计的影响, 选择性忽略了分子振动激发、离解、电离等热化学反应现象的影响, 依然假设为半完全气体, 状态方程有效.
关于比热比变化,图19给出了温度和压力变化对比热比的影响规律. 在可压缩流动中, 实际上仅在高超声速高风洞中才出现γ值变化的问题. 一般在马赫数达到7时, 在喷管设计中就必须要考虑γ的变化了. 而飞行速度或试验气流速度达到Ma=10的 时候, 飞行器头部激波后空气的γ值为1.15 ~ 1.2.γ值较大幅度的变化不仅仅会影响试验测量结果, 而且对高焓喷管设计也会产生显著影响.

图19
Johnson等(1975) 研究了比热比对喷管型面的影响,图20给出了不同比热比条件下, 不同马赫数喷管型线的对比. 显然, 即使具有相同的面积比, 比热比变化引起的喷管出口马赫数相差很大, 显著偏离理想气体的设计结果. 但是, Johnson等在研究固定面积比来对比喷管型线变化时做了一些简化处理, 获得的高焓喷管面积比实际上也受到真实气体效应的影响而具有较大的差别,这一点在唐蓓等(2019)中给出了数值结果说明分析.
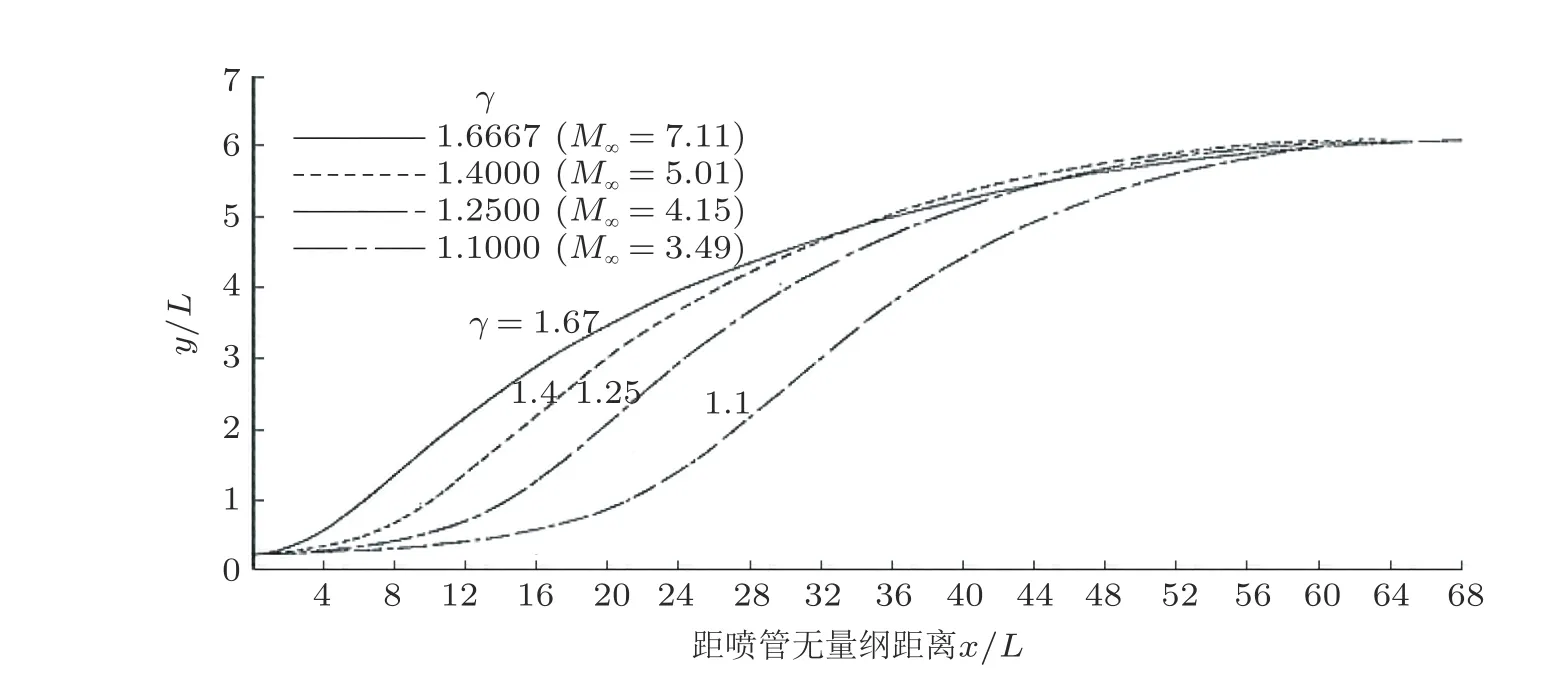
图20
4.2 变比热比MOC喷管设计方法
早在20世纪50年代, 一些学者就对真实气体效应影响下的高超声速喷管设计开展了一系列的研究 (Guentert & Neumann 1959, Enkenhus & Maher 1962, Erickson & Creekmore 1960, Johnson et al. 1963, Johnson et al. 1975). 早期高超声速高焓喷管无黏型线的设计计算依然采用特征线方法, 但是考虑了气体热力学性质的实际变化, 将比热比变化作为影响设计的一个主要参数. 然后将计算出的位移厚度叠加到无黏的喷管型线上, 确定最终喷管物理壁面的型线. 易仕和等(2013)认为仅考虑比热比变化, 忽略其他影响因素, 这本身就做了太多的简化. 但是, 考虑比热比γ变化的影响, 改进传统MOC喷管设计, 对早期的高焓喷管设计研究还是比较现实且实用的办法.
Guentert等(1959)提出了一套高焓轴对称喷管无黏型线设计方法. 该方法通过应用带有可变等熵指数的MOC方法, 计算带有化学反应的高焓气体流动. 随后, Enkenhus等(1962)也提出了计算高温反应气体的轴对称喷管型线设计的类似方法, 独立开发了考虑真实气体效应的喷管设计计算程序. Johnson等(1963)对以上方法进行了改进, 将等熵膨胀的热力学数据直接用于MOC计算方法, 并设计了一套马赫数17、总温2 800 K的轴对称喷管.
Korte (2000)研究了一种相对简化的变比热比的喷管设计方法, 无黏位势流型线采用基于Sivells法的MOC方法设计. 在变比热比喷管设计过程中 (如图8所示), 首先计算HIEG区域的流场, 比热比γ1采 用此区域的平均值, 可得到初始膨胀段型面曲线HG; 然后计算ABCD区域的流场, 比热比γ2采 用该区域的平均值, 计算得到消波段型面曲线AD; 最后计算比热比变化后需满足的面积比要求, 由此确定直线段GA的 长度, 使得初始膨胀段型线HG、 消波段型线AD、直线段GA匹配且满足以下面积比公式要求. 由于采用平衡流假设, 基于等熵关系式推导面积比公式由下式给出 (Eggers 1949)
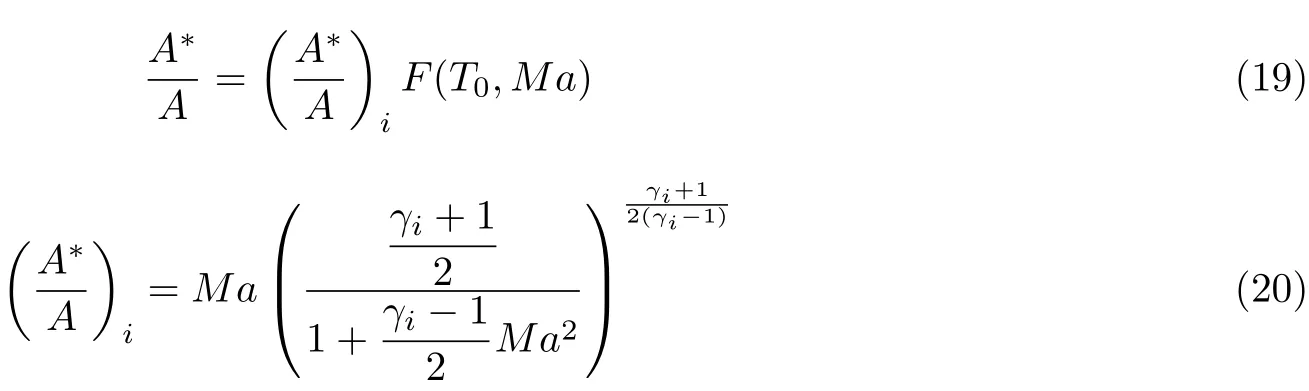
式中,A∗和A分 别为喷管喉道和喷管出口面积; (A∗/A)i为 理想气体条件的面积比, 下角标i表示理想气体;Ma为 设计马赫数,θ为振动特征温度, 与气体组分有关. 在不考虑比热比变化时, 有

当考虑比热比变化时,F(T0,Ma)用下式表示 (Eggers 1949)
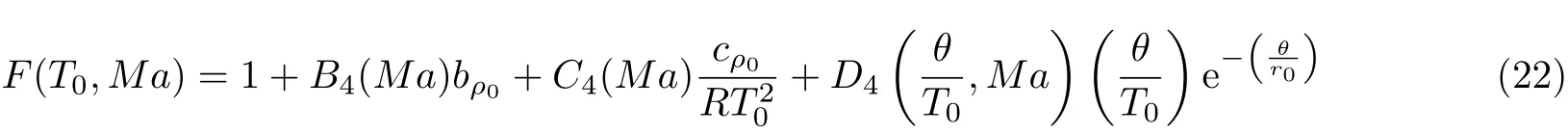
式中

P/P0,ρ/ρ0,T/T0由一维流动一系列等熵关系式得出, 详细推导过程参见Eggers等(1949)文章.
易仕和等(2013)的著作中对上述分析计算过程进行了简化, 如在面积比计算中忽略式 (22)中的B4和C4项, 但结果表明, 对马赫数为6的喷管, 设计得到了较好出口流场. 简化后的方法设计流程相对简单, 适用于工程应用.
实际上, 比热比变化对喷管流动上游 (尤其是喉道附近)的影响要远大于下游流场 (消波段至喷管出口区域), 因为下游流场气体已经膨胀到近似理想气体, 所以重点考虑源流区的高温效应问题是很必要的. 但事实上对于高焓喷管流动的下游气体基本处于冻结状态. 但是, 喉道附近气体组分复杂, 基本处于化学非平衡状态. Zonars (1967)给出了理论评估的平衡流和非平衡流喷管壁面压力与试验测量的对比, 指出随着总温的提高, 非平衡效应越来越明显(图21). 因此, 对于非平衡喷管流动的评估和分析处理变得更为棘手. 对于高焓喷管设计采用仅仅考虑比热比变化的MOC方法也将带有一定的设计误差, 尤其是对于超高速喷管, 设计误差变得很大, 需要寻求新的设计方法或采用CFD数值计算技术辅助的喷管型线优化方法, 以达到喷管设计要求.
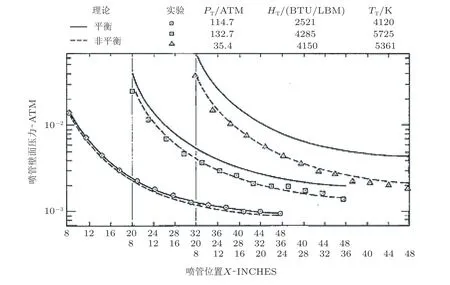
图21
4.3 基于CFD技术的高焓喷管设计方法
4.3.1 CFD/OM设计的研究发展
在高焓气体流动中, 比热比是一个变量, 一些在完全气体假设条件下推导出的流体力学公式就不再适当. 仅仅考虑比热比变化而忽略其他因素影响, 将必然产生较大误差. 随着计算机技术和计算方法的发展, 采用基于CFD数值技术结合优化算法的高焓喷管优化设计方法(CFD/OM), 并进行设计流场确认具有现实意义. 真实气体效应在采用CFD数值计算技术时更容易实现, 成为基于CFD计算技术的喷管设计方法的优势. 即使应用商业数值模拟软件, 考虑使用合适的化学反应模型、试验气体反应组分, 也可对高焓喷管整体流场进行评估计算.
Korte (1991)是较早将CFD数值计算技术应用到高超声速高焓喷管的优化设计中的学者,他提出的基于CFD的分析优化方法可以允许在设计过程中使用任意CFD求解器和优化算法的组合. 对于高焓喷管的设计, 所要做的是只需要更换一个带有不同高温化学反应非平衡流动模型的CFD求解器, 即可对相应高焓条件下的喷管进行高精度的型面设计. Korte采用喷管设计程序CAN-DO (Korte 1992d)设计了一套氦气驱动激波风洞马赫数15喷管, 但对喷管流场分析所采用PNS求解器并没有考虑真实气体效应问题. 随后, Korte等(1992c)与Hollis (1992)利用CAN-DO软件对NASA兰利中心22寸氦气驱动激波风洞喷管进行了设计. 但是仅仅是对CFD求解器中的状态方程进行了简单修改, 所得到的结果基本满足当时的应用要求. 2000年, Korte(2000)在他的设计方法中对受真实气体影响的喷管面积比进行了改进. 基本思路是对给定的马赫数条件, 求解一个定常一维流动, 通过不断迭代, 直到能得到一个期望的喷管出口条件(图22).
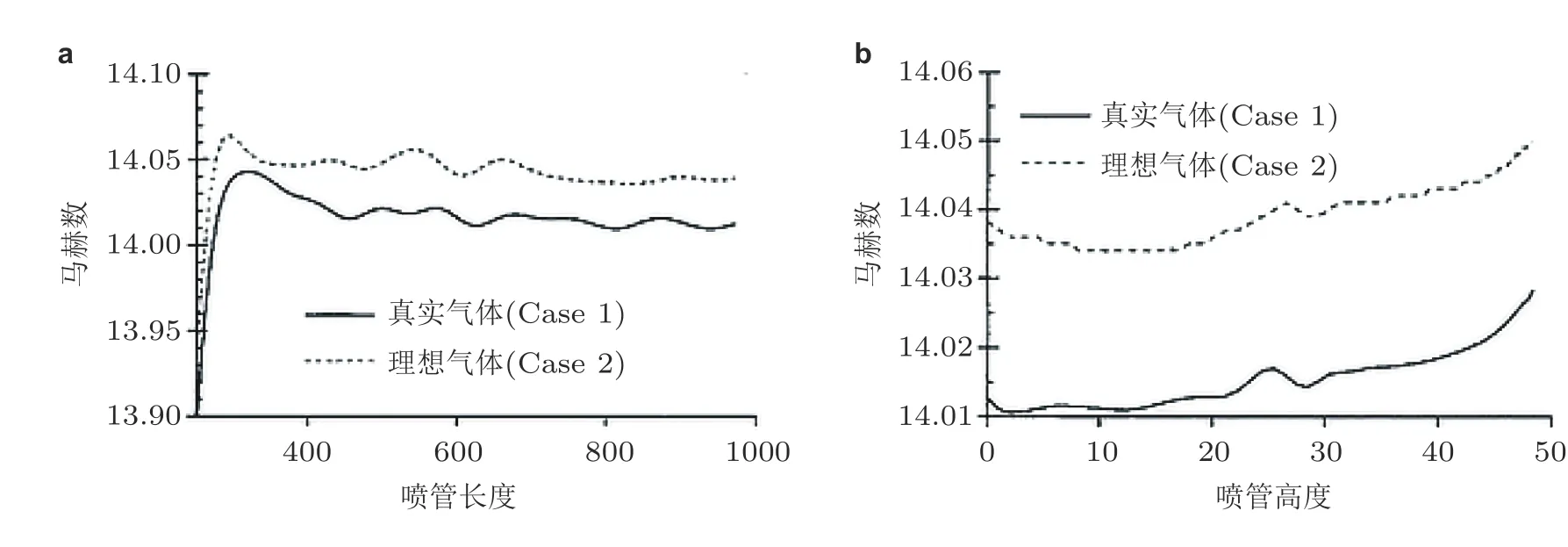
图22
Shope (2004), Shope和Tatum (2005)针对高焓喷管的化学反应流动, 采用了基于CFD计算技术的分析优化设计方法, 并编写完成了喷管设计新的特征线跟踪程序代码, 并能切换多个优化算法, 如最小二乘优化 (Scales 1985)、样条插值优化 (Conte et al. 1972)等. Shope喷管设计程序在Korte等程序基础上, 实现了化学反应流动喷管的扩展并可对样条点进行修正, 其CFD求解器采用一个名为DPLR (data-parallel line relaxation)的计算方法, 能够求解带有化学反应的N-S方程 (Wright 1998; Candler 2004, 2005). DPLR对量热完全气体求解时, 冻结状态的气体组分包括CO2, H2O, N2, O2和NO, 组分的百分比信息采用NASA格伦研究中心 (GRC)的CEA96程序(Gordon & McBride 1996)得到. Shope优化方法流程大致分两步: 第一步是采用基于MOC方法的Sivells方法设计喷管初始型线, 特征线计算过程中假设喷管流动气体为热和量热完全气体, 再通过设置比热比和气体常数得到近似热动力学平衡流的喷管出口设计参数, 如马赫数和速度; 第二步是进一步优化所得到的初始特性型线, 以突破MOC的应用局限性. 主要的设计流程是对喷管型线坐标的样条插值修正. 样条曲线仅仅通过沿喷管初始型线的几个定义点, 而不是对型线的所有坐标点进行插值. 样条插值修正的目的是允许足够数量的坐标点用于描述高精度的喷管型线, 同时仅使用几个节点 (设计参数)进行校正. 然后, 使用这组设计参数重复优化过程 (MOC设计过程), 以进一步提高流场品质. Shope采用该套程序设计了阿诺德工程发展中心 (AEDC)APTU (aerodynamic and propulsion test unit)马赫6喷管, 得到了较为理想结果, 但该方法没有设计过更高马赫数的高焓喷管(图23).

图23
Gaffney (2006, 2007)设计了NASA的HYPULSE激波风洞的高焓喷管. 他采用了Euler方程求解器, 通过调整比热比, 设计了Ma=15喷管. 尽管他采用了传统MOC方法设计流程, 但是得到的设计结果基本满足了设计要求. Chan等(2018) 把基于化学非平衡CFD计算技术的优化设计程序应用于澳大利亚T4高焓激波风洞Ma=10喷管的设计当中, 也得到了较为理想的流场品质. 但是从他们对比研究结果可看见, 低马赫数 (Ma=4, 7)的喷管设计结果, 其数值计算和试验数据对比吻合度要明显优于高马赫数 (Ma=10)的情况.
4.3.2 CFD/MOC/OM设计的探索与讨论
如果期望得到高品质的高焓喷管流场, 喷管设计必须考虑真实气体效应. CFD计算技术结合优化方法以及传统特性线方法边界层校正设计流程是目前风洞喷管设计最主要的两种数值辅助设计方法 (即CFD/OM和CFD/MOC/OM). 当喷管壁面边界层非常厚时, CFD/OM设计方法则是相对可以得到更为好的结果. 但是, 对于反射式脉冲型风洞, 喷管壁为冷壁面且流动压力极高,边界层厚度较薄, 这种情况下使用经典的MOC/BL也可获得较为满意的设计结果. 由于精确地模拟薄喷管边界层所需的计算网格更加精细, 对CFD计算技术也是一个挑战. 相对传统MOC喷管设计方法, 嵌入优化方法的CFD设计流程非常耗时. 在高焓喷管设计方面, 中科院力学所的激波与爆轰物理团队 (以下简称力学所激波团队)基于超大尺度高焓激波风洞设备的建设, 在高焓喷管设计方面探索了一套CFD辅助设计及其优化方法 (CFD/MOC/OM)并投入使用. 该团队选择了对经典MOC/BL方法进行改进, 以设计包括真实气体效应的脉冲型风洞的高焓喷管, 并采用CFD数值计算对设计喷管流场进行模拟, 然后提取数值数据代入MOC/BL中, 再进行迭代优化 (唐蓓等2019). 该方法不同于传统MOC/BL, 也没有采用程序更为复杂的CFD/OM方法.CFD/MOC/OM将CFD数值计算、MOC/BL和优化方法三者结合到设计流程中, 是一种简单的组合式优化解决方案. 该团队采用CFD/MOC/OM, 针对马赫数为17的超高速高焓喷管进行了设计和迭代优化. 在高温气体效应修正时, 不仅考虑比热比的变化, 还考虑非平衡流动组分变化的影响. 对于ABCD区域 (见Sivells法示意图), 由于比热比基本不发生变化, 选取区域平均值进行计算. 对于TIEG区 域, 计算流场时考虑比热比γ随温度的变化, 并且采用NASA拟合多项式进行计算 (McBride et al. 1993, McBride et al. 2002).

式中各个组分的系数可通过查表得到, 其组分信息则通过高精度非平衡流CFD计算提取. 计算面积比时需要用到振动特征温度, 可以通过CFD计算流场提取出相应区域组分获得, 再由计算振动特征温度得出高焓喷管的喉道与出口面积比. 初始CFD数据信息和计算条件, 则通过传统方法较为粗略计算无黏型线得到的CFD喷管流场中提取. 在后续的数次迭代计算中, 流场参数将渐渐收敛, 一般2 ~ 3次迭代计算即可得到较为满意的结果. 对于超高速喷管, 其焓值也特别高的情况, 可适当增加迭代次数(图24).

图24
CFD/MOC/OM方法包含两个较为重要的设计技术. 一是对超高速高焓喷管面积比基于CFD数值数据的拟合. 由于传统喷管流动面积比的理论公式是针对平衡流动的情况, 非平衡流CFD计算所得实际的出口马赫数与设计马赫数存在较大偏差. 为了得到更准确的无黏流场, 对平衡流得出的理论喷管面积比进行了拟合修正.图25中三角点为各马赫数条件下采用式 (19)计算所得面积比, 方块点为该面积比在非平衡CFD计算获得的实际出口马赫数. 利用面积比与其实际出口马赫数的关系进行曲线拟合, 在拟合曲线中提取出各马赫数所对应的新面积比 (圆点),然后代入程序重新设计喷管型线. 经过几次迭代计算后, 得到最终的面积比, 使设计马赫数与实际马赫数一致. 实际上对于面积比的拟合过程是对非平衡喷管流动边界层发展的相对更为准确的评估过程. 二是实现了满足条件的端点斜率可控埃尔米特样条插值优化, 获得的样条曲线总体上和原设计给出的参考点十分接近, 优化后的曲线消除了参考点的局部波动等问题 (罗长童等2019). 事实上, 在高焓喷管设计中, 为保证喷管出口流场性能, 喷管型线需满足以下条件: (1) 单调递增; (2)一阶导数光滑 (二阶导函数连续); (3) 喷管型线过定义坐标点且在定义点处一阶导数和二阶导数为零或可控; (4) 可实现对喉道段、分段连接点等处更精细的连接控制, 避免型线中出现间断点. 现有的优化方法进行全局拟合、逐点分段局部拟合或插值时, 较难实现样条插值的自由控制.
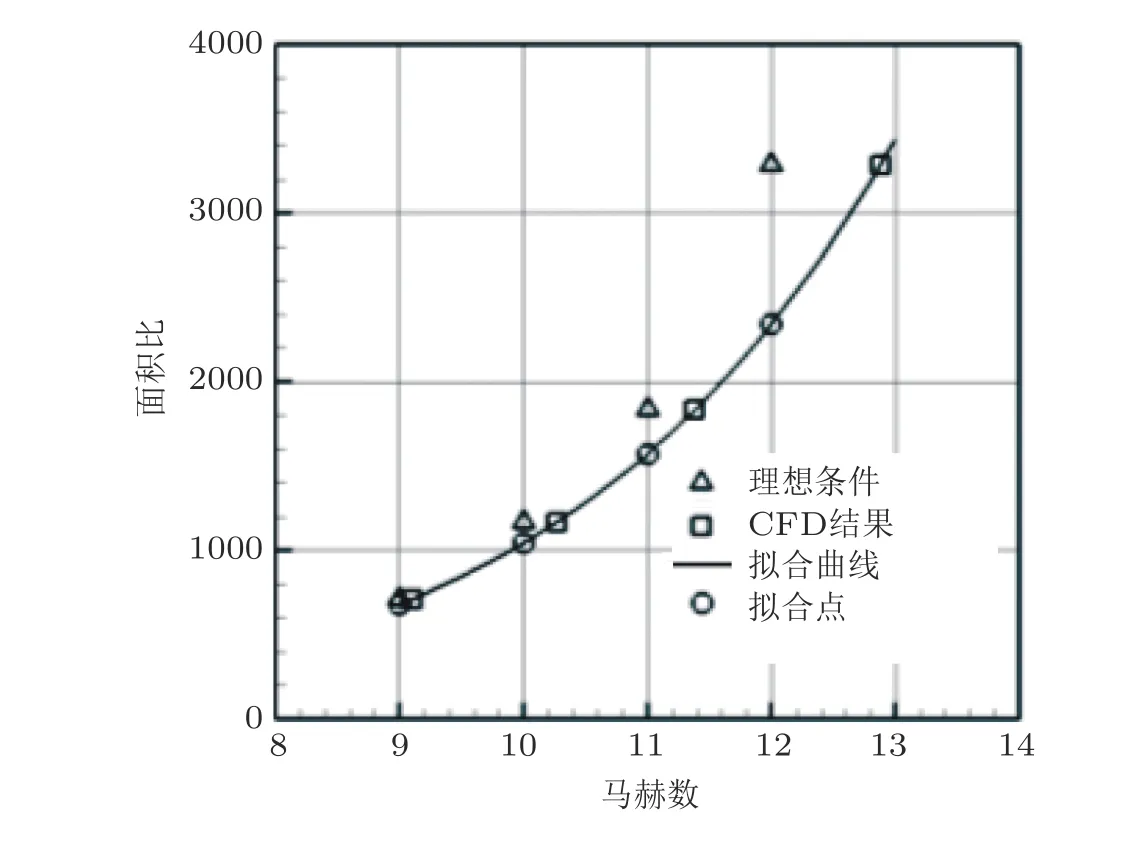
图25
在方法的可靠性验证方面, 针对CFD/MOC/OM喷管设计优化方法, 力学所激波团队针对该团队的JF-12复现飞行条件激波风洞 (以下简称JF-12复现风洞)喷管, 采用CFD数值计算、MOC/BL和优化方法三者结合的优化设计方法, 进行了大量的设计验证工作. 首先利用已有的JF-12复现风洞直径Φ=1.5 m、名义Ma=6的喷管进行了程序验证, 以确保计算条件及设计方法的可靠性. 针对3种不同设计喷管模型做了CFD数值模拟, 并进行了详细的对比分析. 模型1是JF-12复现风洞的名义Ma=6现服役喷管, 采用其流场试验对CFD程序进行验证; 模型2是按传统MOC/BL设计和边界层修正的Ma=6喷 管, 直径Φ=1.5 m; 模型3是按CFD/MOC/OM优化设计方法设计的Ma=6喷管. 对比模型2计算得到的流场结果 (见图26和表1), 模型3按新型方法优化修正的喷管型线, 在此工况下得到的流场品质较好, 喷管出口流场均匀区马赫数更接近设计马赫数, 且流场均匀性更好, 能够得到较高品质的试验段气流.

表 1 M a=6喷管流场马赫数均匀性 (唐蓓等2019)

图26
基于以上激波风洞喷管设计方法的对比分析, 低总温条件的常规高超声速风洞喷管设计难度要远低于超高速高焓喷管的设计. 激波风洞对来流模拟的目标是要尽可能复现高超声速飞行器在相应海拔高度的飞行条件, 这也是高焓风洞建设者和研究学者共同期望的最终目标. 但是要在地面试验设备中实现对所有高焓流动参数的复现是极其困难的, 甚至在目前研究阶段是不可能实现的. JF-12复现风洞在该目标的实现中走出了突破性的一步. 在该风洞研制中, 针对飞行马赫数5 ~ 9、高度25 ~ 50 km的飞行条件进行了高超声速喷管的设计和应用. 基于JF-12复现风洞试验气体总焓条件并未达到气体的完全解离和电离条件, 事实上其喷管设计难度介于常规低总温条件高超声速风洞与超高速高焓 (如总温4000 ~ 10 000 K)激波风洞之间. 尽管在相应试验流动中振动激发效应已经比较明显, 但对于该风洞喷管的设计, 采用传统的MOC/BL方法, 结合喉道区域的比热容比变化 (不考虑化学反应影响), 即可达到设计要求和使用性能. 实际上, 对于总温条件低于2000 K的情况, 考虑比热容比变化与否对喷管设计结果并没有十分显著的影响.然而, 对于可达到气体解离的高焓情况, 仅考虑比热容比的变化就已经对喷管的型线产生较大的影响, 大部分情况应该考虑喷管流动中的化学非平衡影响. 因此, 针对高焓喷管的设计, 首先要考虑实际飞行条件给出设计参数, 并基于总焓参数选择相应的理论、数值以及两者结合的喷管设计方法, 更需要根据实际情况发展适用的创新设计方法. 但是, 基于目前阶段的研究水平, 或将在今后相当长一段时期内, 针对超高速高焓条件的喷管设计, 结合现有的理论方法, 采用CFD数值辅助设计是当前相对较为理想的技术手段.
5 总结与展望
高超声速喷管设计已经取得了许多重要进展, 相关的理论和方法可以分为三类: 第一类是传统特征线方法与边界层修正相结合的MOC/BL方法, 从1929年MOC方法提出后不断发展并沿用至今. 对于不考虑高温气体影响的常规高超声速风洞喷管和马赫数较低的高焓喷管, 应用该方法均可以得到不错的设计结果. 但是传统MOC方法对高超声速高焓喷管设计是存在局限性的,而且其改进后的方法也很难满足目前越来越高的评估标准. 于是, 喷管流场求解从MOC方法转向具有更高精度的CFD数值模拟技术. 第二类方法是基于CFD计算技术的优化方法CFD/OM,即将优化方法嵌入到CFD求解器的设计方法. CFD/OM方法从20世纪90年代初提出, 随着计算技术提升而不断发展并衍生出多种CFD求解器与优化算法的耦合方式. 这些方法是优化算法与CFD求解器的深度耦合, 突破了传统方法的拘束, 把边界层和真实气体效应的影响也通过CFD求解一并完成, 不必再进行边界层和高温气体影响的修正. 但是, 该方法对CFD求解器与优化算法的耦合技术要求苛刻, 计算成本也高, 不易于工程领域的推广应用. 第三类方法是基于CFD数值计算技术的MOC优化设计, 即CFD/MOC/OM. 该方法是针对第二类方法设计流程复杂的问题, 为了简化设计而发展的方法. 对于高焓喷管初始无黏位流型线的设计依然使用技术成熟、简单易用的MOC方法完成, 通过化学非平衡流动的CFD数值模拟计算, 优化高焓喷管型线. 该方法化解了优化算法与CFD求解器的高度耦合难题, 每一迭代步后得到的CFD数据作为MOC设计的初始和边界条件代入求解, 方法简单、应用方便、鲁棒性好, 一般2 ~ 3次迭代即可得到较为满意的优化结果.
高超声速喷管设计从理论解析、半经验公式近似求解、边界层修正 (MOC/BL), 到基于CFD辅助设计技术的优化方法 (CFD/OM和CFD/MOC/OM), 高超声速喷管设计的精确度越来越高. 尤其是对于高焓喷管设计, 基于CFD数值计算技术的优化方法凸显优势. 从喷管设计理论与方法的发展历史来看, 它随计算机技术和计算方法的发展而提高, 受航空航天技术需求的推动. 从21世纪初开始, 尤其是近十年, 高超声速飞行技术成为未来宇航工业的核心技术, 对超高速和高焓试验流场品质的要求也越来越高, 使得20世纪研制的多数高超声速高焓地面模拟设备面临性能提升的需求, 也推动了新型超高速风洞的研发, 所以高超声速喷管设计理论和方法的研究也越来越重要. 回顾近百年的研究进展, 在高超声速喷管设计领域, 下述几个方面是非常需要深入探索的.
(1) 单纯应用MOC/BL方法的喷管设计已经不能满足超高速高焓风洞喷管的设计要求, 但它与CFD数值计算结合的优化设计方法, 还是可以获得品质较高的高焓流场, 所以对MOC/BL方法做进一步改进还是有价值的, 如基于Sivells方法设置轴向速度或马赫数分布的办法仍然可以得到相对满意的结果.
(2) 可考虑将高精度高焓流动试验数据作为喷管优化设计依据或设定边界条件是值得探索的方法. 主要考虑两种方式: 一种是基于已设计完成喷管的试验数据, 对其喉道位置处的型线进行修正. 该方式简单直接, 但成本相对较高, 需要加工完成喷管后再对其进行部分“再设计改造”;另外一种是将高焓流场数据做为设计参考条件, 采用CFD模拟技术进行修正优化的喷管设计方法. 该方法可针对不同焓值、不同马赫数等流场参数, 把相应的试验测量数据作为参考条件进行设计优化.
(3) CFD/OM优化设计方法的流程复杂、计算成本高, 但是随着计算机技术的发展, 优化算法嵌入高精度CFD技术的设计方法还应该是未来的发展趋势. 因CFD辅助设计方法过度依赖于数值计算的精度水平, 并且对于高焓流动的高精度模拟能力也存在很大的挑战, 所以热化学非平衡流动过程的高精度CFD数值技术也需同步发展. 这其实要求CFD求解器所使用的化学反应模型也要基于更为精准的高焓流动试验数据进一步改进和发展.
此外, 在高超声速喷管设计过程中, 一些科学前沿问题也值得进一步深入探讨, 诸如: (1)高超声速飞行器的发展问题, 其中包括军用高超声速飞行器、民用高超声速客机以及水平起降完全重复使用的天地往返运输系统. 这类高超声速飞行器的发展离不开高品质地面试验研究, 而地面试验风洞设备所能提供的飞行模拟条件的优劣直接决定了试验结果的可靠性, 从而决定飞行器研制的成败. 从另外一个角度, 高超声速飞行器的高速发展也大大增加了高超声速地面试验设备的使用需求, 越来越高性能的流场指标要求需要更高品质的高速喷管支撑, 自然促使喷管设计方法的不断发展; (2)高温真实气体效应的影响机制问题. 该问题几十年来一直困扰着高超声速飞行器研制, 其对飞行器气动特性的影响大大制约了其快速发展. 其根本原因是现有地面模拟设备很难对高温效应进行精确模拟, 使得到的气动试验结果变得不可靠, 而更棘手的是人们至今对真实气体效应的影响机制无法从理论、模拟和试验给出合理的、精确的评估和解释. 这个问题同样促使高焓喷管设计技术和方法亟需得到发展, 从而可以使人们从本质上认识一系列高温现象, 推动高超声速技术进一步发展, 促进高速飞行器的快速开发和研制.
在相应的实验技术发展方面, 无论直接测量技术还是间接测量技术, 在高焓风洞中的应用至今仍然有诸多问题难以突破, 使得其测量性能和效果远低于常规低速风洞或者常规高超声速风洞. 其中, 一个重要原因是高焓风洞基本上都以瞬态脉冲型风洞为主, 其测试时间非常短 (短至微妙量级), 并且试验流场的均匀性较低速风洞差, 因此对测试技术和设备都提出了严苛的要求和条件. 但从另外的角度, 这个问题的存在也促使测试技术和测量设备不断的创新发展. 同时, 也促使高超领域研究学者对能够产生更高流场品质的高焓喷管不断探索和深入研究设计方法, 从而设计研制出符合更高试验指标要求的高焓高超声速喷管.
高超声速喷管设计理论和方法及其评价涉及面非常广泛, 需要综合理论、计算、实验方面的有效手段, 是一个很具难度的研究领域, 至今依然具有挑战性. 通过高超声速喷管设计, 提高试验流场的品质, 由此提高高超声速试验数据的精准度和可靠性是非常有意义的, 对于先进空天飞行器的发展同样具有重要支撑意义. 所以, 高超声速喷管设计理论和方法的研究具有基础性, 应该受到高度关注.
致 谢国家自然科学基金(11672357, 11727901)资助项目.

