期望核辐射剂量下移动机器人的路径规划

赵恒柱 杨明翰 邓多成 汪建业 杨子辉

1（中国科学院合肥物质科学研究院 合肥 230031）

2（中国科学技术大学 合肥 230027）

核能作为一种清洁环保、稳定高效的新型能源，在我国经济与能源可持续发展中具有重要的战略地位。在核工业中，对于那些暴露于放射性环境的员工，核辐射是潜在的风险。虽然核设施和系统在设计之初都会采取必要的措施来保护核电厂工作人员的安全与健康，但无论设计多么复杂，辐射暴露都是不可避免的［1］。据统计，中国核电厂员工在正常运行的日常工作中所承受的吸收剂量占中国核电厂年总剂量的20%，而在核电站大修过程中其所承受的吸收剂量占核电厂年检总剂量的80%［2］。与此同时，随着计算机技术和人工智能的快速发展，使用机器人在核辐射环境下完成运输、探测和检修等作业具有广阔的应用前景。用涉核机器人替代辐射环境中的人工作业具有重要意义，但是延长涉核机器人使用寿命、提高应用性价比等方面也面临一些潜在的困难与挑战。在放射性环境中，机器人会因受到超量辐射发生通讯中断、传感器失效等问题而无法继续作业。根据辐射防护理论，涉核机器人的核防护除了考虑机器人的电子器件、传感器和信号通讯系统等受辐射影响较大的部件材料选型外，还需要采取外部辐射防护措施［3］。外部辐射防护的基本方法是减少机器人在放射性环境中的停留时间，扩大机器人与辐射源之间的距离。因此我们有必要为涉核机器人设计一种路径规划方案，以确保他们受到最少的辐照［4］。

路径规划就是机器人根据自身传感器对环境的感知，自行规划出一条安全的运行路线，同时高效完成作业任务［5］。机器人路径规划的核心是规划算法，常用的路径规划算法有A*算法［6-7］、人工势场法（APF）［8］、快速随机扩展树（RRT）算法［9］和概率路线图（PRM）算法［10］。A*算法是一种基于启发式函数的搜索算法，该算法精巧、高效，在给定的代价函数和环境标识下，只要路径存在，就能找到一条最短路径［11］；APF在进行路径规划时，不需要提前生成完整路径，只需要根据当前姿态以及周边障碍物来确定下一步的运动，算法反应速度快、计算量小，便于实时性控制，但容易出现目标不可达和局部极小值的问题［12］；RRT算法是基于采样的方式，具有很强的搜索性，只要环境中存在可行路径，RRT算法就能够从中找到一条可行路径，但正是因为它的随机性也带来一些缺点，如扩展过程中随机树生长方向较随机，导致算法搜索效率低，收敛速度较慢，且在动态环境下缺乏稳定性和偏离最优解等问题［9］；PRM算法主要分为两个阶段：采样阶段和学习阶段［10］。PRM方法是概率完备的，这意味着当时间趋于无穷时，它一定会找到解决方案。该算法在没有障碍物明确信息的情况下，也可以构建出可行轨迹的路线图。但当采样点太少或分布不合理时，可能无法找到最优解。计算具有复杂几何图形的精确解或大型场景规划时，所需时间可能呈指数倍增［13］。

本研究的路径规划背景是机器人在封闭核辐射环境中作业，需要考虑机器人的运动特性，路径规划要求具有较少的转折点。减少机器人转向次数不仅可以节省机器人电量，而且可以减少运动时间，因此减少路径中的转折点是急需解决的问题［14］。本研究提出了一种以吸收剂量为代价的改进型平滑A*算法。算法融合了范围内障碍物的数量和位置信息，提高了搜索的灵活性和效率，并在最后将生成的路径进行平滑优化，剔除冗余拐点，使得到的路径更加符合机器人运动特性。

1 传统A＊算法

传统A*算法是一种典型的启发式搜索算法，其结合了迪杰斯特拉最小路径算法（Dijkstra）和广度优先遍历算法（BFS）的优势［15］，以在搜索过程中找到相对最优解。传统A*算法的优势在于：在选择下一个扩展节点时，综合考虑当前实际代价和候选扩展节点的预估代价，选取最小总代价的点作为新的节点。其代价函数形式见式（1）。

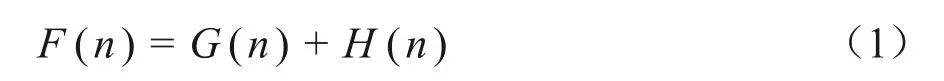
式中：F（n）为起始节点经候选节点到目标节点的总代价；G（n）为起始节点到候选节点实际的代价；H（n）为候选节点到目标节点的估计代价。

2 改进的A＊算法

传统A*算法主要用来解决全局路径规划最优问题，其约束条件往往只有障碍物和最短路径，所得到的路径曲线存在节点冗余、折线多、耗时长等缺点，增加了机器人作业时的负担和损耗，严重降低了工作效率［16］。为此，本文提出了以吸收剂量为代价的一种改进平滑A*算法。该算法基于网格地图数据，如图1所示，黑色为障碍物，白色为自由空间，综合考虑核辐射场的剂量率、障碍物、路径长度和拐点数等因素，以机器人受到的吸收剂量为代价，采用八方向搜索方式［17-18］，如图2所示，使生成的路径不仅符合避障和低吸收剂量的要求，还满足移动机器人运动的非完整约束条件［7］。

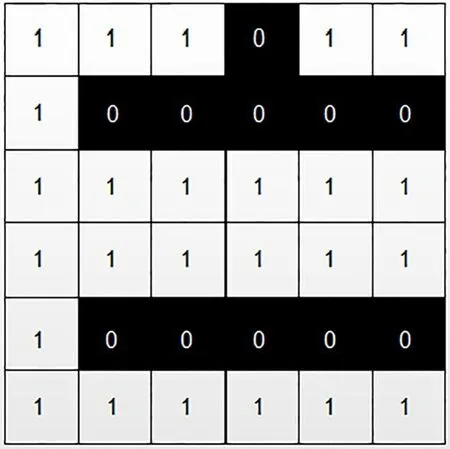
图1 基于网格的地图模型Fig.1 Grid based map model

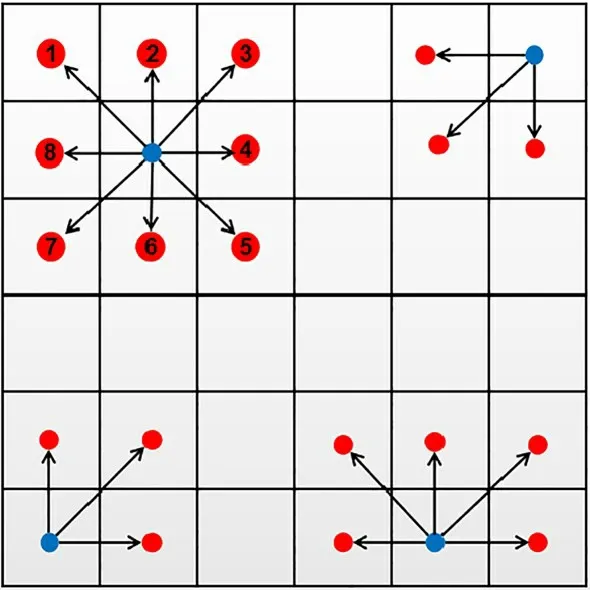
图2 八方向搜索Fig.2 Eight direction search

2.1 代价函数

改进的A*算法选用吸收剂量作为代价，此时，累计代价G（n）表示从起始点到当前节点n的机器人所受到的实际吸收剂量，估计代价H（n）表示从当前节点n到目标终点机器人所受到的估计吸收剂量。假设机器人移动速度恒定为v，栅格的长度为l，并取两个相邻栅格之间的累计剂量是这两个栅格剂量率的平均值乘以机器人运行时间，通过计算机器人在任意两相邻节点间移动时受到的吸收剂量之和，得到该路径的累计代价。则G（n）可表示为式（2）。

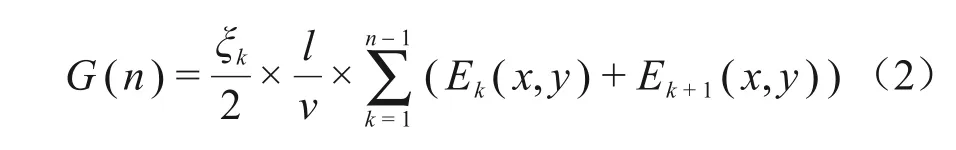
式中：Ek（x，y）、Ek+1（x，y）分别表示节点k、k+1的剂量率，μSv/s；分母上数字2为计算相邻两节点剂量率的平均值时得到的；ξk为移动距离系数，当移动方向为水平或者垂直方向时（图2中的2、4、6、8），ξk取1，当移动方向为对角线时（图2中的1、3、5、7），ξk取1.4。

启发函数是A*算法中最重要的寻路依据，决定了搜索方向和效率［18］，本文定义估计代价H（n）函数见式（3）。

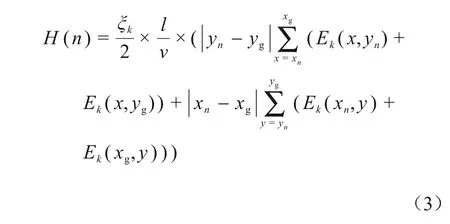
式中：xn、yn表示节点n的横坐标和纵坐标；xg、yg表示目标终点的横坐标和纵坐标，由于搜索方向采用的是图2中的2、4、6、8，故取ξk为1。

根据式（2）和式（3）可得到总的吸收剂量代价函数，见式（4）。

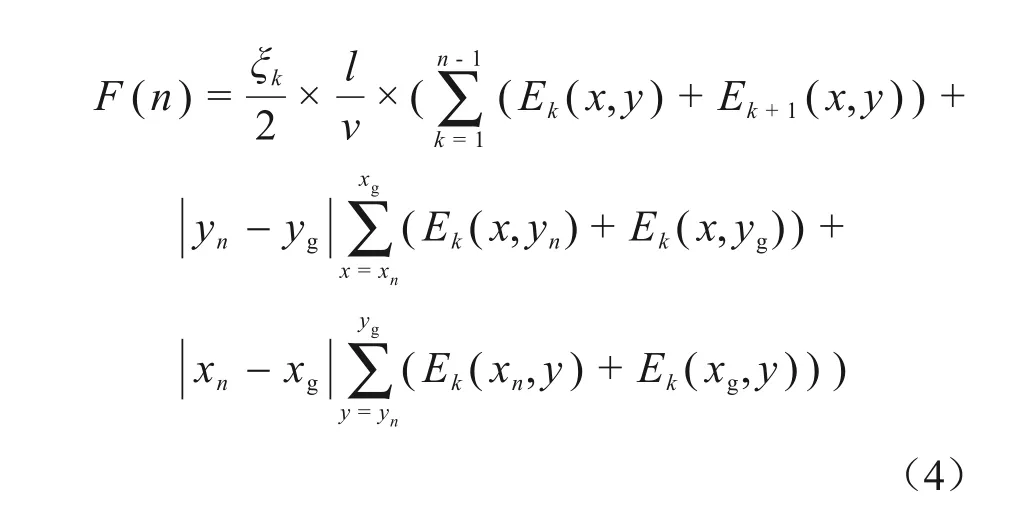
2.2 加权障碍物优化算法

2.2.1 自适应步长

步长是A*算法中重要的一个参数，传统A*算法采用固定步长，带来扩展节点多，计算量大等问题。本文通过以节点n所在的网格为中心，建立邻域矩阵，并经过对从3阶到10阶矩阵的实验测算，发现5阶矩阵预判效果最佳，且生成的路径更为平滑，故选用5×5的邻域矩阵，加权障碍物数量实现动态调节步长大小，提高路径规划的灵活性，矩阵的形式见式（5）。

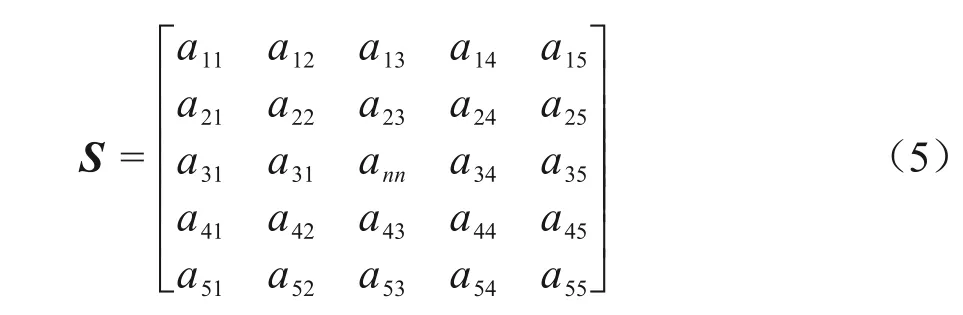
节点附近的黑色网格代表障碍物，白色网格为自由节点，在矩阵中对应位置写入元素1、0。令E=（1，1，1，1，1），则ET=（1，1，1，1，1）T，则邻域内障碍物总数M可表示为式（6）。

由式（6）可得可调节步长的计算公式（7）。

式中：D为自适应步长，考虑到5阶邻域矩阵预判的局限性，分别取步长最小和最大值为：Dmin=l，Dmax=3l；β为障碍物影响系数，经实验对比发现，当β∈（0，1/8）时，得到路径的扩展点更少，故取β∈（0，1/8）。

2.2.2 启发信息加权

在A*算法中，估计代价函数很大程度决定生成路径的质量，传统A*算法在计算总代价时，不考虑周围障碍物的情况，取权值为1，这使得路径在障碍物附近转折点较多，影响机器人移动效率。本文提出一种针对估计代价函数加权的改进算法，根据节点周围障碍物的数量来决定权值的大小，由式（7）可得，障碍物加权的权值计算公式见式（8）。

式中：ω为总代价中估计代价的权值；α为障碍物系数，通过实验测算，当α∈（0，1/8）时，权值控制在［1，3］，增大了启发信息对总代价的影响，生成的路径拐点较少，得到的路径更平滑。故取α∈（0，1/8）。改进后的总代价函数计算公式见式（9）。

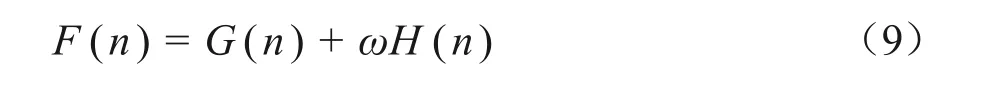
2.2.3 改进后A*算法的寻路过程

改进后的A*算法的工作流程图如图3所示。

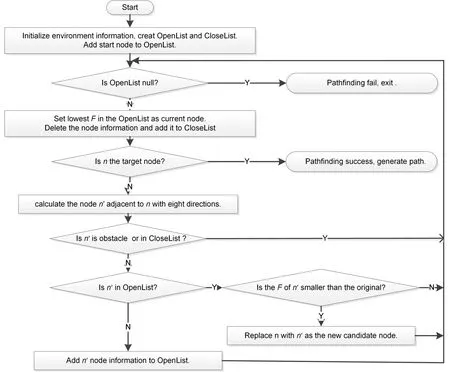
图3 改进型A*算法流程图Fig.3 Flow chart of improved A*algorithm

寻路前初始化地图信息，包括起始点、目标点和障碍物，并创建OpenList和CloseList，用来存放相应节点信息。机器人从起点S出发，通过式（5～8）得到D、M、ω的值，然后根据M的大小选择扩展的步长，得到相应的扩展节点，判断这些扩展节点是否为障碍物或者超过了吸收剂量率限等效而成的障碍物，若是则丢弃这些扩展点；反之，计算节点的D、M、ω大小，并将它们和节点一同加入OpenList，然后将OpenList找到F值最低的节点设为候选节点，从OpenList删除该节点信息并添加到CloseList，判断该点是否为目标点G，若是则寻路成功并生成路径；若不是，则重复上面的过程，直到找到目标点G或者OpenList为空，结束寻路。

2.3 路径平滑优化

经过障碍物加权优化的A*算法生成的路径扩展节点较少且安全无碰，但仍存在路径不平滑和总转折角度较大的问题，这使得机器人实际工作中将消耗更多的电能和时间。针对此问题，本文提出一种平滑优化方法，能有效提升路径平滑性，进而提高机器人作业效率，优化前后路线如图4和图5所示。其中图4中路径由八方向搜索得到，对比可知，优化后的路径扩展点和累计转折次数更少，路径平滑度显著提高。

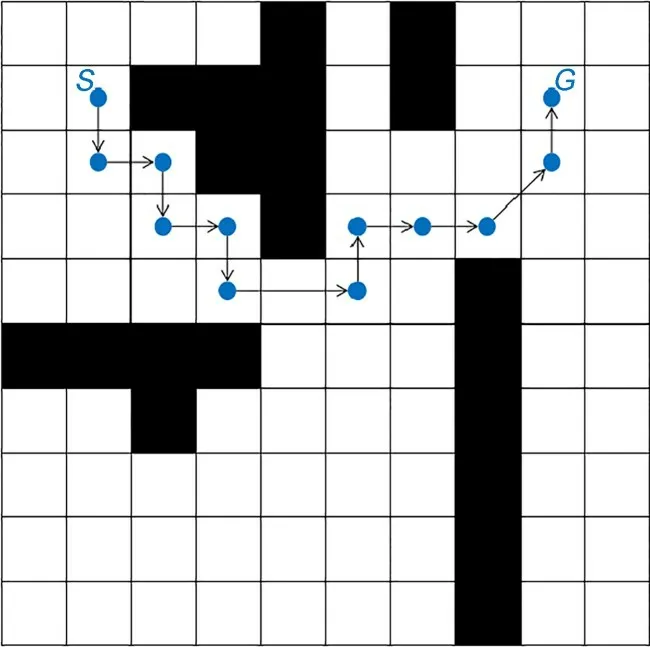
图4 优化前的移动路径Fig.4 Move path before optimization

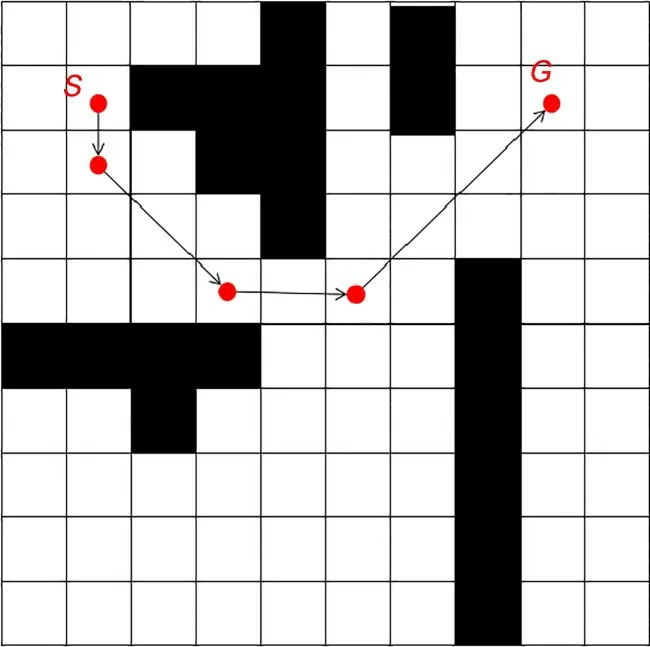
图5 优化后的移动路径Fig.5 Optimized movement path

图4中S点为起点，G点为目标点，节点ni为CloseList中保存的节点，i为节点标号（i≥1），设置变量k（k=1），黑色网格代表障碍物，白色网格为可扩展网格节点。平滑优化路径的具体步骤：Step1，连接起点S和目标点G，得到直线段LSG，若LSG没有穿过障碍物，则删除CloseList中所有节点并跳转到Step4；Step2，连接节点nk和节点ni，得到直线段Lki，若Lki没有穿过障碍物，则将中标号从k到i-1节点全部删掉并跳转到Step4；Step3，k增加1。当k等于i-1时，i减少1。若i等于1，则退出循环，反之跳转到Step2；Step4，从起点开始，经过CloseList中的节点，直到目标点，连接所得的曲线就是平滑优化后的路径。

3 仿真验证与分析

为验证本文提出的改进平滑A*算法在核辐射环境下移动机器人路径规划中的可行性和有效性，在中国科学院中子输运理论与辐射安全重点实验室关于核辐射环境中路径规划技术研究的基础上，选取了国内某一核电站厂房为环境模型，进行仿真实验［19-20］。同时，为验证算法的改进效果，分别在无障碍物和有障碍场景下进行实验。仿真实验在MATLAB R2014a实验平台上进行。计算机配置：CPU2.2GHz，内存8GB。利用中子输运设计与安全评价软件系统SuperMC进行环境建模和中子输运计算，得到吸收剂量场数据［21-23］。选取10m×10m方形区域，等分成50×50栅格地图（网格间距0.2m），机器人移动速度取3600m/h，起始点和目标点坐标分别为（3，10）和（39，35），进行多组传统A*算法与改进平滑A*算法的对比实验。

图6（a）和（b）分别是在无障碍物和有障碍物场景下，传统A*算法与改进后A*算法（未引入障碍物加权优化和平滑优化）的实验结果，图6（c）是仅引入障碍物加权优化后的实验结果，图6（d）是同时引入加权障碍物优化和平滑优化后的实验结果。

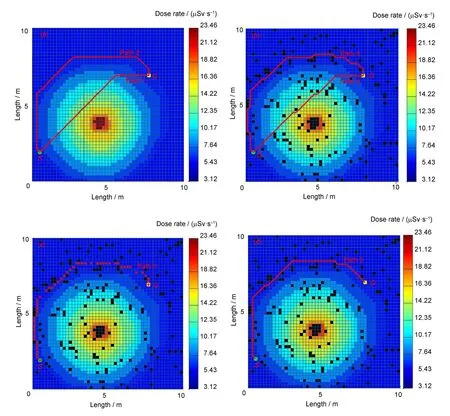
图6 不同场景仿真结果：(a)场景一算法改进前后对比；(b)场景二算法改进前后对比；(c)加权优化；(d)加权及平滑优化Fig.6 Simulation results of different scenarios:(a)comparison of scene one algorithm before and after improvement;(b)comparison of Scene two algorithm before and after improvement;(c)weighted optimization;(d)weighting and smoothing optimization

将不同场景下传统A*算法与改进平滑A*算法仿真得到的实验数据进行对比，结果如表1所示。

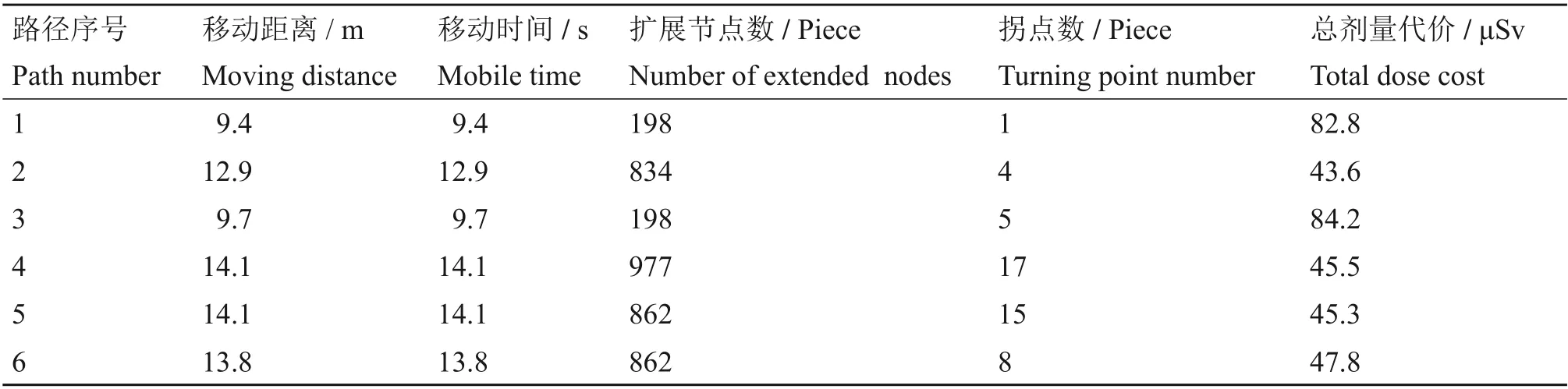
表1 传统A＊算法与改进平滑A＊算法的实验数据对比Table1 Experimental data comparison between traditional A＊algorithm and improved smooth A＊algorithm

由表1可知，与传统A*相比，在无障碍物和有障碍物场景下，未引入障碍物加权优化和平滑优化的改进A*算法生成的路径总剂量代价减少比例均大于45%，但路径仍存在因扩展节点和拐点数较多造成的搜索效率和平滑度较低的问题；仅引入障碍物加权优化后，总剂量代价基本不变，搜索效率和平滑度均提高11.8%；同时引入障碍物加权优化和平滑优化后，总剂量代价虽然增加5%，但搜索效率提高11.8%，平滑度提高52.9%。因此，本文提出的改进平滑A*算法在核辐射环境下规划出来的路径更加安全、高效和平滑，可应用于涉核机器人的路径规划。

4 结论

随着计算机技术和人工智能的快速发展，各种满足核工业任务需求和核事故场景的机器人不断被研制出来并投入使用。本文提出的改进平滑A*算法，经过多次实验对比表明，生成的路径不仅平滑和可靠，且能有效降低核辐射场景下机器人作业过程中受到的辐照，在延长涉核机器人使用寿命、提高应用性价比等方面具有重要的意义。后续将考虑对路径中冗余节点进行优化，从而进一步提高涉核机器人的运行效率。

致谢 感谢中国科学院合肥物质研究院的陈春花、孙国民、戈道川等老师的帮助以及乏燃料后处理科研专项经费的支持。