结构不平衡交跨线路悬垂串张力特性仿真研究

吕中宾，叶中飞，田 瑞，祝志磊

(1.国网河南省电力公司电力科学研究院，河南 郑州 450052；2.华北电力大学机械工程系，河北 保定 071003)

1 引言

随着输电线路的建造数量在不断地增加，不可避免的使得跨越高速铁路、高速公路和重要输电通道的重要交叉跨越(三跨)线路不断地增多[1，2]，在交叉跨越线路上的事故也频频发生，例如已发生事故的线路有220kV肖辛线(跨高铁)和500kV瓦海二线(跨高速公路)。重要交叉跨越线路的安全性不仅关系到该条跨越输电线路的运行，也影响着被跨越线路或交通的安全运行，因此提高重要交叉跨越线路的安全性对电力线路运行和交通安全保障具有重要意义。

现阶段关于重要交叉跨越线路的研究，主要体现在线路正常运行时交叉跨越线路周围工频电磁场的计算[3-9]、交叉跨越距离的测量[10，11]和发生事故时交叉跨越线路故障电流的计算[12，13]三个方面。文献[3]基于模拟电荷法和毕奥-萨瓦定律分别计算了交叉跨越导线下方产生的工频电场和工频磁场。文献[10]利用机器视觉测量技术和数字图像处理方法，对交叉跨越线路的跨越距离进行了测量。文献[12]提出了一种交叉跨越线路故障短路电流的计算方法。但是目前对于分析交叉跨越线路的力学特性，以防止事故发生的研究则很少。

随着输电线路运行时间的增加，线路金具中的球头挂环和碗头挂板处往往会发生腐蚀、磨损或者严重变形等情况，使得连接处不能转动，而倾向于刚性连接。针对于长期运行线路的这一特点，研究长期运行条件下的交叉跨越线路中，结构不对称特性(交叉跨越线路中跨越档和邻档的档距或高差不同)对大风工况下的悬垂串张力特性的影响规律，以防止线路悬垂串上的连接金具在大风工况下发生受力破坏情况(掉串事故)的发生。

本文以某220kV“耐-直-耐”形式的独立耐张段交叉跨越线路实际工程为背景，建立其三塔四线有限元模型，利用线性滤波法模拟大风工况下的脉动风时程曲线。通过改变交叉跨越线路段的邻档档距和高差，研究在大风工况下线路自身结构不对称特性对长期运行的交叉跨越线路导地线悬垂串最大动张力的影响规律，旨在为提高交叉跨越线路长期运行的安全水平提供参考。

2 大风工况风速时程模拟

大气边界层风的瞬时风速U(t)可看成是平均风速U和脉动风速u(t)的叠加。

2.1 平均风速U

平均风速随离地高度z的变化曲线被称为平均风速剖面(Mean Wind Speed Profile)。平均风速剖面的指数律计算公式如下

U(z)=U10(z/10)α

(1)

式中，U(z)为离地z米高度处的平均风速，m/s；U10为离地10m高度处的基本风速，m/s；α为地面粗糙度指数。本文对交叉跨越线路的大风工况进行数值仿真计算，其大风工况的基本风速为28.81m/s，地面粗糙度类别为B类，则对应的地面粗糙度指数α为0.15。

脉动风速可看作是一种零均值的各态历经的高斯平稳随机过程[14，15]。我国建筑结构荷载规范(GB50009-2012)使用的风速功率谱为Davenport谱[16]，其表达式为

(2)

(3)

式中，k为地面粗糙度系数；U10为离地10m高度处的基本风速，m/s；f为脉动风频率，Hz。本文采用线性滤波法对Davenport谱进行脉动风速时程的模拟[17，18]，模拟主要参数见表1。

表1 脉动风速时程模拟主要参数

利用线性滤波法且考虑脉动风的空间相关性，模拟出的酒杯型直线塔顶部的脉动风速时程曲线如图1(a)所示，其脉动风速功率谱如图1(b)所示。由图可知，模拟出的脉动风速的功率谱曲线和目标谱(Davenport谱)基本重合，证明了利用线性滤波法模拟脉动风速的正确性。

图1 脉动风速时程曲线及其功率谱曲线

3 交叉跨越线路有限元模型的建立

3.1 220kV交叉跨越线路实际参数

本文模拟的交叉跨越线路的实际结构如图2所示，由三基输电塔组成，线路结构为“耐-直-耐”形式，耐张塔A和耐张塔C均为干字型铁塔，直线塔B为酒杯型铁塔。耐张塔A和直线塔B之间为跨越档，另一档线路为其邻档。图中①、②和③分别为顺线路方向的右相、中相和左相导线悬垂绝缘子串，④和⑤分别为右地线悬垂串和左地线悬垂串。该段交叉跨越线路的主要参数列于表2中。

图2 “耐-直-耐”交叉跨越线路结构

表2 交叉跨越输电线路主要参数

3.2 结构不平衡交叉跨越线路有限元模型建立

对交叉跨越输电线路建立三塔四线模型，利用BEAM188单元模拟输电塔中的主材和横隔材，用LINK8单元模拟输电塔中的斜材。为模拟长期运行线路中的悬垂绝缘子串，由于在连接处发生腐蚀、磨损或者严重变形等缺陷使得不能转动而倾向于刚性连接情况，本文用BEAM188单元模拟悬垂绝缘子串。由于导地线为柔索结构，用LINK10索单元模拟，实际线路导地线的主要参数列于表3中。

表3 导地线主要参数

本文基于实际线路结构参数(表1)，通过改变邻档的档距和高差，研究交叉跨越线路自身结构不对称特性对大风工况下导地线悬垂串最大动张力的影响规律。邻档档距在300m至400m之间每隔100m取一个值，总共包括实际线路(邻档档距350m)在内共11个不同的档距；通过改变耐张塔C的呼高改变邻档的高差，耐张塔C的呼高在16m至26m之间每米取一个值，总共包括实际线路(耐张塔C呼高21m)在内取了11个不同的呼高，对这21种线路结构的交叉跨越输电线路分别进行有限元建模。

4 计算结果及分析

4.1 大风工况下交叉跨越线路悬垂串张力响应

对实际交叉跨越输电线路进行动态响应分析，得到右相导线悬垂绝缘子串张力的时程曲线(如图4所示)。将直线塔上导地线悬垂串的动态响应最大张力和利用静态分析得出的结果进行对比，对比结果列于表5中。脉动放大比为动态分析中悬垂串动张力的最大值与静态分析结果的比值。从表5中可以看出，在考虑脉动风的影响下，相比于静态分析结果，导线悬垂串张力增大了12%左右，地线悬垂串张力增大了35%左右。虽然导线悬垂串张力的增大百分比要小于地线悬垂串，但导线悬垂串实际张力增大值(1.7kN左右)要大于地线悬垂串(0.8kN)，因此导地线悬垂串张力在脉动风作用下产生的脉动放大效应均不容忽视。

图3 直线塔右相导线悬垂串张力时程曲线

图4 悬垂串最大动张力随邻档档距变化的规格化曲线

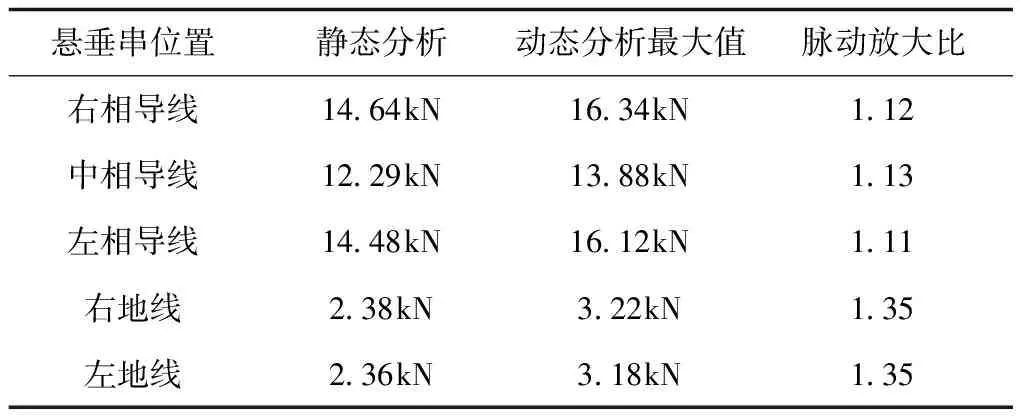
表4 悬垂串张力动静态分析结果对比

4.2 线路结构不平衡对悬垂串动张力特性的影响

4.2.1 邻档档距变化的影响规律

对11种不同邻档档距的交叉跨越输电线路进行动态响应分析，对动态分析结果进行对比分析。表5为不同邻档档距下的悬垂串最大动张力汇总表。从表中可看出，随着邻档档距的增大，在大风工况下导地线的5个悬垂串最大动张力均在逐渐增大。相比于350m的实际邻档档距，400m邻档档距情况下，导线悬垂串最大动张力增大1kN左右，地线悬垂串最大动张力增大0.3kN，可知邻档档距对导线悬垂串张力的影响幅度要大于对地线悬垂串张力的影响。

表5 各邻档档距下的悬垂串最大动张力(单位:kN)

图5为悬垂串最大动张力随邻档档距变化的规格化曲线。纵坐标为每种档距下的悬垂串最大动张力与350m实际档距时的最大动张力的比值，即F/F350。由图可知，导线悬垂串张力规格化值F/F350随邻档档距的变化情况与地线悬垂串几乎一致。当邻档档距从300m增至400m时，导地线悬垂串的F/F350值从0.90增大到1.10，且五条F/F350曲线随档距的变化几乎均成线性变化。

图5 悬垂串最大动张力随塔C呼高变化的规格化曲线

4.2.2 邻档高差变化的影响规律

对11种不同邻档高差的交叉跨越输电线路进行动态响应分析，对动态分析结果进行对比分析。表6为不同塔C呼高下的悬垂串最大动张力汇总表。从表中可看出，随着塔C呼高的增大，在大风工况下导地线的5个悬垂串最大动张力均在逐渐减小。相比于21m的实际塔C呼高，当塔C呼高增为26m时，导线悬垂串最大动张力减小0.73kN左右，地线悬垂串最大动张力减小0.2kN左右。

表6 不同塔C呼高下的悬垂串最大动张力(单位:kN)

图6为悬垂串最大动张力随塔C呼高变化的规格化曲线。纵坐标为每种呼高下的悬垂串最大动张力与21m塔C实际呼高时的最大动张力的比值，即F/F21。由图可知，导地线悬垂串张力规格化值F/F21随塔C呼高的变化曲线几乎均成线性变化，且地线悬垂串的F/F21值变化斜率要略大于导线悬垂串。当塔C呼高从16m增至26m时，导线悬垂串的F/F21值从1.05减小到0.94，地线悬垂串的F/F21值从1.09减小到0.93。

综合对比分析邻档档距和邻档高差对导地线悬垂串最大动张力的影响，可以发现，邻档档距增加50m(从350m增至400m)使得大风工况下的导地线悬垂串最大动张力增大10%左右，而塔C呼高增大5m(从21m增至26m)使得导地线悬垂串最大动张力减小6%左右，由此可得导地线悬垂串最大动张力对邻档高差值的改变更为敏感。

5 结论

本文通过改变交叉跨越线路中的邻档档距和高差，建立不同线路结构的交叉跨越线路有限元模型，并分别对其进行大风工况下的动态仿真分析，研究线路自身结构不对称特性对大风工况下的导地线悬垂串最大动张力的影响规律，可得如下结论：

1)对于实际交叉跨越线路，在考虑脉动风的动态分析下，导线悬垂串的最大动张力比静态分析结果增大了12%，地线悬垂串最大动张力增大了35%，因此在线路抗风设计时不能忽视导地线悬垂串张力在脉动风作用下的脉动放大效应。

2)随着邻档档距的增大，大风工况下的导地线悬垂串最大动张力在不断增大。且导地线悬垂串张力规格化值F/F350随邻档档距的变化曲线几乎成线性增大变化。

3)随着耐张塔C呼高的增大(邻档高差是在不断的减小)，大风工况下的导地线悬垂串最大动张力在逐渐减小。且导地线悬垂串张力规格化值F/F21随塔C呼高的变化曲线几乎成线性减小变化。

4)为防止长期运行的交叉跨越线路在大风工况下发生掉串事故，在设计线路时应适当减小邻档档距，以及减小邻档的高差值(即增大塔C呼高)，从而减小大风工况下导地线悬垂串的最大动张力，提高线路的安全运行水平。并且导地线悬垂串最大动张力对邻档高差值的改变更为敏感，所以在交叉跨越线路的设计时应重点注意邻档高差的取值。