基于免疫优化ICA算法的配电网谐波源定位仿真

江友华，陈明磊，曹以龙

(上海电力大学电子与信息工程学院，上海 200090)

1 引言

为了控制并检测配电网中存在的滤波问题，保护电网的稳定和安全，需要估计谐波源在配电网中的状态和分布，其中配电网系统中谐波的治理、分析和检测是重点研究问题[1-2]。，在实现配电网谐波源定位的过程中，需要全面了解配电网的拓扑结构，但由于网络参数和系统模型的匮乏，在实际工程中难以完成配电网谐波定位任务，使配电网谐波源定位方法成为目前亟需解决的问题。

文献[3]提出一种基于实测数据的配电网谐波源定位方法，将配电网母线的谐波相位和电压幅值当做量测量，在考虑测量误差和建模误差的基础上，通过系统各节点母线阻抗和谐波功率之间存在的符号关系划分母线，根据各节点排序完成配电网谐波源的定位，该方法对谐波源定位所用的时间较长，存在定位效率低的问题。文献[4]提出一种基于分布式传感网络的配电网谐波源定位方法，构建，配电网运行模型，通过独立分量分析方法提取配电网中存在的故障源信号，根据节点之间存在的相关信息数，获得配电网的拓扑结构，实现谐波源的定位，该方法得到的定位结果与实际位置不符，存在定位精准度低。文献[5]提出一种基于梯度投影和客观性测量算法的谐波定位方法，分析配电网系统的拓扑结构，量测量选用支路谐波电流，状态量选用节点注入谐波电流，通过梯度投影法在配电网中完成谐波源的定位，该方法不能精准的计算谐波电流，导致定位精准度低。

由于当前配电网谐波源定位方法存在定位效率低和定位精准度低的问题，提出基于免疫优化ICA算法的配电网谐波源定位方法。

2 配电网模型构建

2.1 基于变压器等效电路的谐波阻抗的计算

在不同配电网结构中都存在主变压器，其主要功能是连接上一级电网，以主动配电网电压水平为基础降低电压[6]。负荷率和额定定容量是配电网的主要参数，配电网结构设计、变压器台数和变压器容量都会受到负荷率的影响。

设Kp代表的是负荷率，其计算公式如下

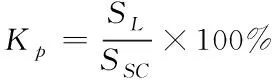
(1)

式中，SSC代表的是变压器对应的额定短路容量；SL代表的是实际运行过程中主变压器对应的最大负荷。

图1为双绕组变压器一般情况下的等效电路。

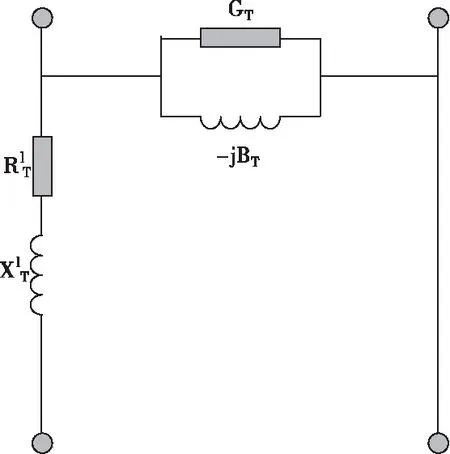
图1 变压器等效电路

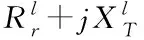
在变压器额定负载电流中，一般情况下励磁电流所占的部分较小，所以在分析配电网变压器时不进行考虑，因此变压器等效电路可以选用阻抗支路，如图2。

图2 简化的变压器等效电路

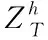
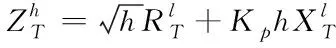
(2)

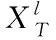
2.2 输电线路等效集中参数模型

配电网是一种低压配电网，包括大量的地下电缆和架空电路，架空线会影响城市环境的美观，且占据了部分土地面积，地下电缆可以解决上述问题，满足人们的需求[8]。

在输电线路中存在的电阻电感分布均匀，基于免疫优化ICA算法的配电网谐波源定位方法，根据谐波在各个节点中的分布情况，选用等效集中参数模型。

等效集中参数模型中较为典型的是π型等效电路，如图3所示。

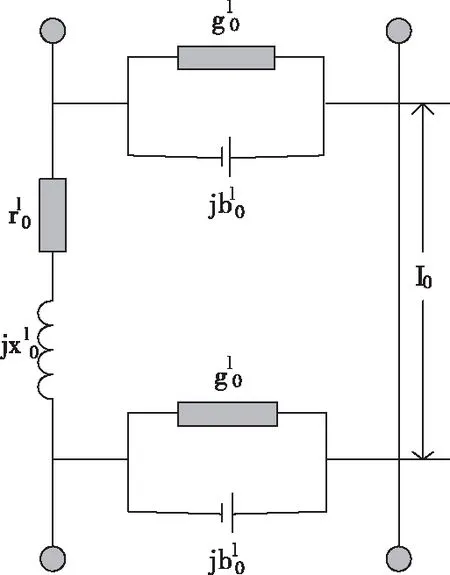
图3 π型分布参数等效模型

图中，l描述的是输电线路在电路中的长度。

设r0代表的是单位长度的电阻；b0描述的是电纳；L0代表的是电感；g0为电导；x0为电抗，线路的电导在实际运行过程中是相当小的，所以可以考虑忽略不计，当输电线路在配电网中的长度为l时，得到的等效集中参数有

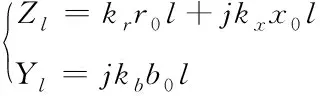
(3)

式中，kr、kx、kb均为集中参数和分布参数之间的换算系数，受线路特性的影响[9]。

3 配电网谐波源定位方法

3.1 原子分解法

在完备的原子库中获取状态较好的原子，利用原子分解法，表达所选原子信号的线性度，原子分解法与传统方法不同，自由性较高，可以自适应的在信号特征的基础上，选取基展开函数，增强了信号表达的灵活性和简洁性[10]。基于免疫优化ICA算法的配电网谐波源定位方法，通过原子分解法表达配电网中的谐波信号。

下式为Gabor原子对应的实数表达式

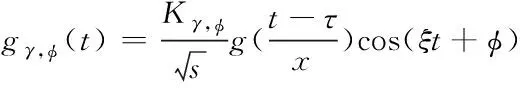
(4)

式中，Kγ，φ描述的是原子归一化因子；g(t)代表的是高斯窗函数；s代表的是预定标因子；τ代表的是位移因子；φ代表的是相位因子；ξ代表的是频率因子；γ代表的是原子的索引，其表达式如下

γ={s，τ，ξ，φ}

(5)

为了使计算速度不受到大规模原子库的影响，通过离散化原则处理长度为N的信号[11]。频率间隔Δξ和时间间隔Δτ之间满足下式

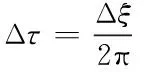
(6)

设a代表的是伸缩因子，通常大于1。对原子的索引进行离散处理，得到下式

γ=(aj，paj，Δτ，ka-jΔξ，φ)

(7)

Gabor原子库离散处理后的表达式如下：

gr(n)=gj(n-p2j)cos(nkπ21-j+φ)

(8)

n={0，1，…，N-1}

(9)

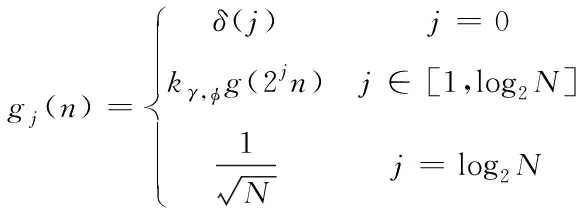
(10)

信号fR，m通过MP算法进行处理，分别在信号和原子库中获取最佳原子能量grm和最佳匹配原子grm，获得新的残余信号fR，m+1，当迭代次数或设定值大于残余信号时，终止[12]。

待处理信号和原子的内积值最大时即为选取最佳原子的条件，即

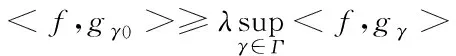
(11)

式中，f为等待处理的配电网谐波信号；gγ0代表的是最优原子；λ描述的是优化因子，在区间(0，1)内取值；sup 为取最大值操作；gγ代表的是原子库中存在的原子；γ描述的是原子gγ的索引。

原信号f经过N次迭代处理后的表达式如下

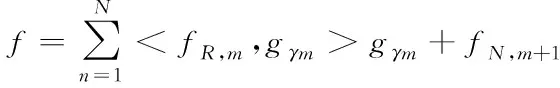
(12)

式中，fR，m代表的是残余信号，是通过m-1次迭代后获得的；gγm代表的是经过m次迭代后获得的最优匹配原子。通过上述过程实现配电网中谐波信号的系数分析，获得谐波信号中存在的相关信息，为配电网谐波源的定位提供依据。

3.2 基于免疫优化ICA算法的谐波定位

基于免疫优化ICA算法的配电网谐波源定位方法，通过免疫优化ICA算法在配电网中实现谐波源的定位。

1)谐波电流

不考虑谐波电压在配电网中的测量噪声，通过下述线性方程描述在节点中注入的谐波电流

Ih=YhVh

(13)

式中，Ih代表的是在节点中注入的谐波电流向量，谐波电流在配电网中会引起电压畸变，导致谐波电流注入线性负荷节点中，增多了需要在配电网中估计的谐波源总数，式(13)中的Ih描述的是将非线性负荷作为配电网谐波源注入到节点中的谐波电流；Yh代表的是系统导纳矩阵；h代表的是谐波次数；Vh代表的是谐波电压向量。

难以在高频谐波下获取系统参数Yh，如果未知系统参数Yh，可以通过免疫优化ICA算法进行求解，在计算谐波电流时，估计谐波电流需要满足非高斯性和相互统计独立性。

2)谐波源定位

互信息在信息论中是一个信息度量，有效性较高，可以描述两个变量之间存在的关联性，并且对变量间存在的相关性进行量化。

假设由xi构成随机变量X，由yi构成随机变量Y，其中i=1，2，…，n。设I(X，Y)代表的是随机变量X和Y之间的互信息，其计算公式如下

I(X，Y)=H(X)+H(Y)-H(X，Y)

(14)

设H(·)代表的是随机变量对应的熵，可以对变量的不确定度进行衡量，熵值H(·)随着变量分布离散度的增大而增大。设H(X)代表的是随机变量X对应的熵，其计算公式如下

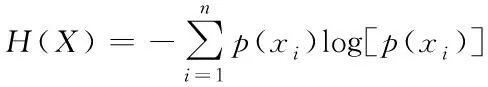
(15)

式中，p(·)代表的是密度函数。

设H(X，Y)代表的是随机变量X和Y之间的联合熵，其计算公式如下

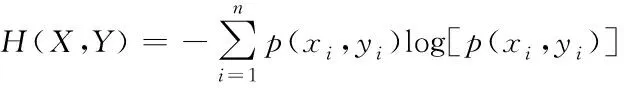
(16)

互信息I(X，Y)描述的是将随机变量Y引入随机变量X的不确定度减小的量。

如果随机变量X与Y的相关度越高，表明随机变量X随着变量Y的引入不确定度减小的量不断增大，即互信息I(X，Y)的值也随之增大。根据上述分析可知，通过计算能够得到的谐波电压和谐波电流之间存在的互信息，获取谐波电压在谐波电流互信息为最大值时对应的节点，即为配电网谐波源的位置，实现配电网谐波源的定位。

4 实验结果与分析

为了验证基于免疫优化ICA算法的配电网谐波源定位方法的整体有效性，需要对所提配电网谐波源定位方法进行测试，本次测试的网络环境为IEEE-14Bμs，其节点结构示意图如图4。实验配电网发电环境选取某配电所的真实发电环境，如图5所示。

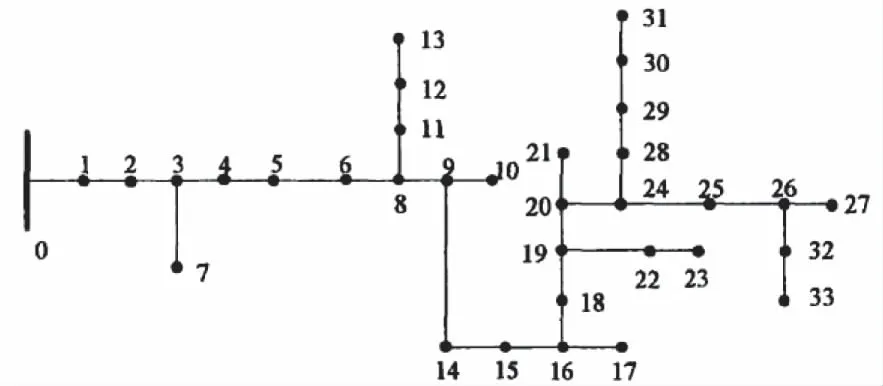
图4 IEEE-14Bus节点系统

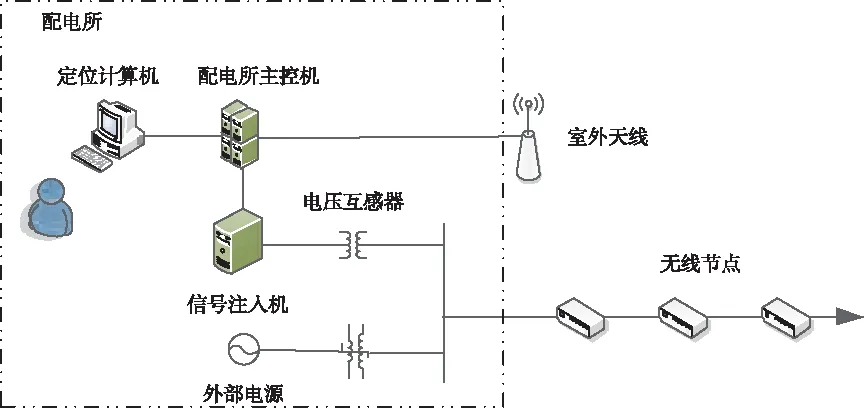
图5 配电模型框架

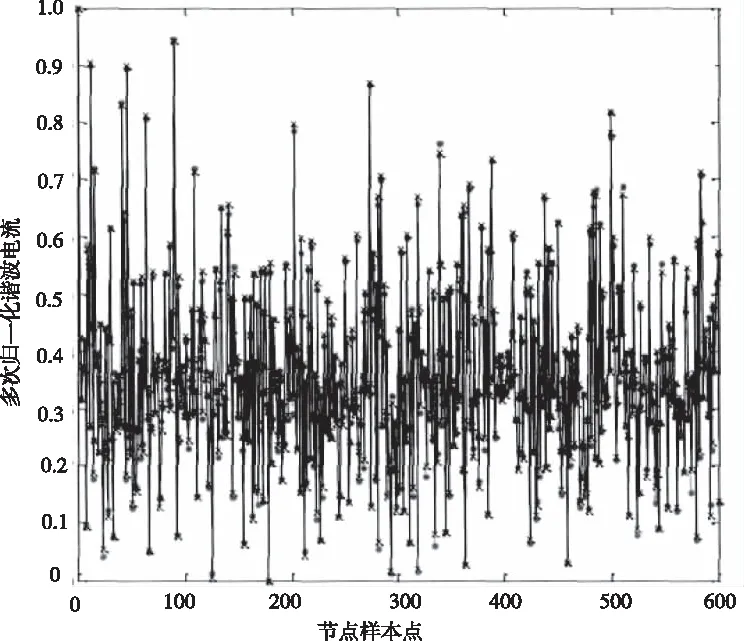
图6 实验谐波样本

为了验证基于免疫优化ICA算法的配电网谐波源定位方法的整体有效性，采用基于实测数据的配电网谐波源定位方法、基于分布式传感网络的配电网谐波源定位方法作为对比，对配电网中的谐波电流进行测试，并将测试结果与实际结果进行对比，三种方法的测试结果如图7。

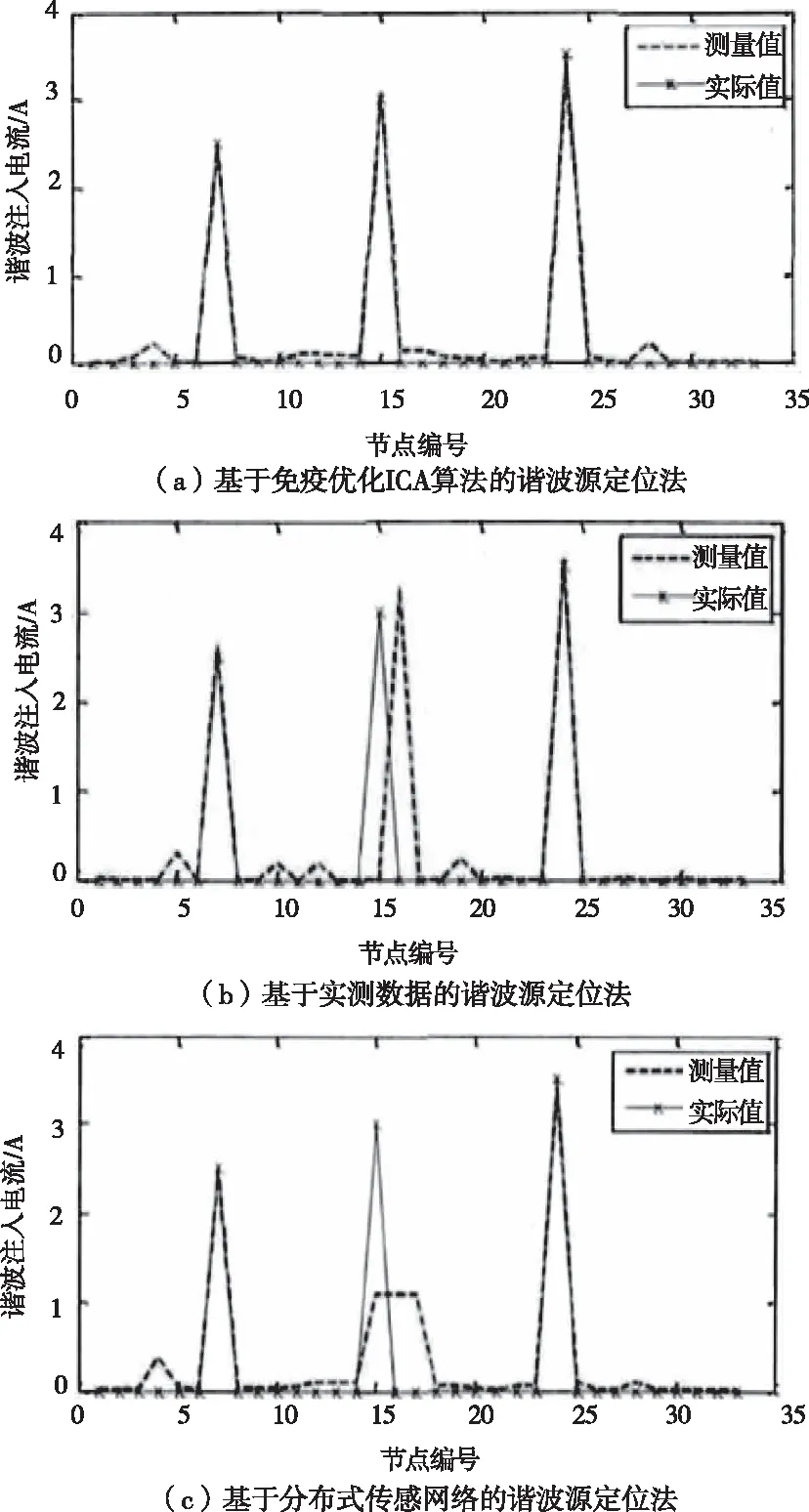
图7 不同方法下谐波电流定位对比

分析图7可知，采用基于免疫优化ICA算法的配电网谐波源定位方法计算得到的谐波电流与实际谐波电流基本相符，与实际谐波电流相比采用基于实测数据的配电网谐波源定位方法和基于分布式传感网络的配电网谐波源定位方法计算得到的谐波电流误差较大。通过上述分析可知，基于免疫优化ICA算法的配电网谐波源定位方法可精准的测得谐波电流在配电网中的值，谐波电流的精准度直接影响了配电网谐波源定位的结果，验证基于免疫优化ICA算法的配电网谐波源定位方法的定位精准度较高。

5 结束语

配电网的建设和我国产业的发展，在配电网中增加了大量的负荷，导致配电网中出现了大量的谐波，使配电网谐波源定位方法成为目前研究的热点。当前配电网谐波源定位方法存在定位效率低和定位精准度低的问题，提出基于免疫优化ICA算法的配电网谐波源定位方法，该方法通过构建配电网模型获取谐波相关信息，在短时间内精准的在配电网中完成谐波源的定位，为我国配电网的发展提供了保障。