复杂车路环境下自动驾驶车辆换道仿真研究

禹乐文，罗 霞，刘仕焜

(西南交通大学交通运输与物流学院，四川 成都 611756)

1 引言

自动驾驶车辆换道决策的算法设计十分具有挑战性，但对确保自动驾驶车辆的安全平稳运行至关重要。从国际公认的SAE(美国汽车工程协会)制定的L0-L5自动驾驶车辆阶段分级划分标准[1]不难看出，在实现部分自动化(L2)以及有条件自动化(L3)后，想要进一步将自动驾驶自动化程度进一步提升至高度乃至完全自动化(L4、L5)，需要进一步提高场景适用性。而保证自动驾驶车辆在复杂车路环境下的正确换道决策则是提高其实用性的关键。

换道决策规划主要是针对具有换道意图的车辆，根据实际情况进行“是否换道”的决策[2]。决策模型可分为基于规则的模型、基于机器学习的模型、基于效用计算的模型和基于博弈论的模型[3]。基于规则的模型，以Gipps[4]理论为代表，车辆的跟驰换道与否取决于车辆是否满足规则所限制条件。Barcelo等人[5]在此基础上增加了新的换道条件。此种模型将复杂的换道决策简化为固定准则的判断，实用性不强。基于效用计算的代表性模型由Ahmed等人[6]和Toledo等人[7]提出。Sun等[8]提出了在不同换道场景下基于效用函数的换道选择模型。此类算法能够较好地模拟换道决策过程，但却忽略了周围车辆对于换道车辆的反应预测；基于机器学习的模型效果较优，但对数据需求量较大，实用性受到限制。此类模型的算法包括人工神经网络、模糊逻辑、决策树等[9-11]。

相较于上述方法，博弈论可以在保证算法效率的同时，尽可能全面考虑环境参数以及周围车辆的不同反应对于换道决策的影响。Yoo和Langari[12]提出了一种基于Stackelberg博弈的模型来研究车辆在换车道和合并车道过程中的相互作用。Wang等人[13]使用博弈论方法预测车辆的换道跟驰控制。Liu等人[14]使用非合作博弈对车道并入进行仿真。Yu[15]提出了一种基于动态博弈的变道模型。但上述模型大多将与周围车辆的博弈简化为与目标车道后车的博弈，仍然没有做到“复杂车路环境”下的决策。

针对现有文献的局限性，本次研究将综合考虑变道车辆、目标车道车辆和原车道车辆之间的关系，提出一种适用性更高的驾驶决策算法，实现AV-HV(自动驾驶车和人类驾驶车)环境下自动驾驶车辆的高效安全驾驶。

2 模型总述

现阶段模型所考虑的情况一般如图1(a)所示，在如图1(b)所示的复杂车路环境下，一般模型缺乏适用性，而此情况，在实际驾驶环境中更为常见，这需要综合考虑换道车辆与原车道、目标车道前后多辆车的冲突关系。

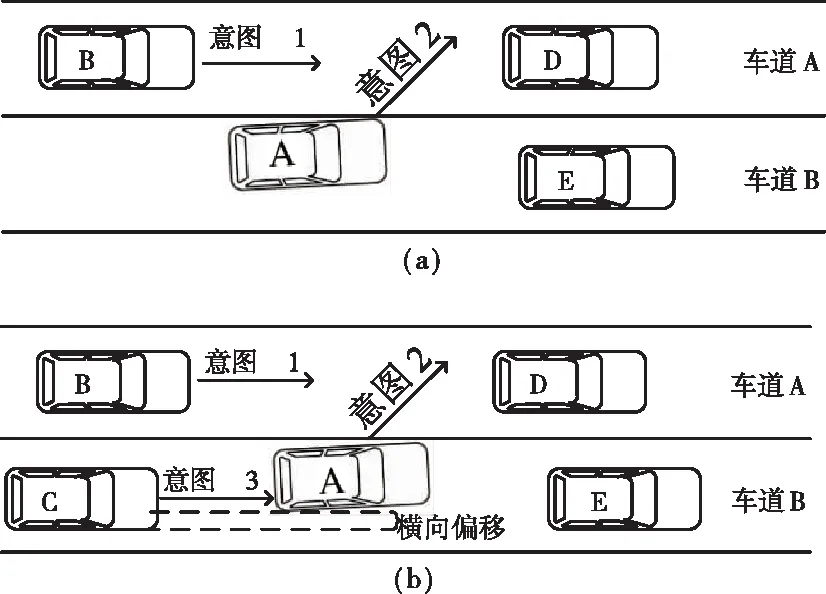
图1 不同路况下车辆换道意图示意

具体分析，1(b)所描述的情况如下：两个相邻的车道A和车道B上同时存在两个AV-HV车队，自动驾驶车A产生换道意图，车道A的目标间隙是否适合换道与间隙大小和B的侵略性有关。在图1(a)中，当A进行一定的横向运动时，若目标车道内的后车侵略性较大，且无意避免冲突，则会返回原车道行驶。而在图1(b)中，A的横向移动，会导致车C将产生超车意图，这与车辆A的意图相冲突。针对上述情况，本文综合考虑了换道车辆与原车道、目标车道前后多辆车的冲突关系，通过引入车辆侵略系数来量化复杂路况下周围车辆对于换道决策的影响，以寻找自动驾驶车辆在复杂车路环境下的换道决策以及轨迹线规划的最佳策略，从而保证所有车辆在换道决策过程中的安全和效率。模型算法逻辑如图2所示。下面，将针对各个部分具体阐述模型算法。

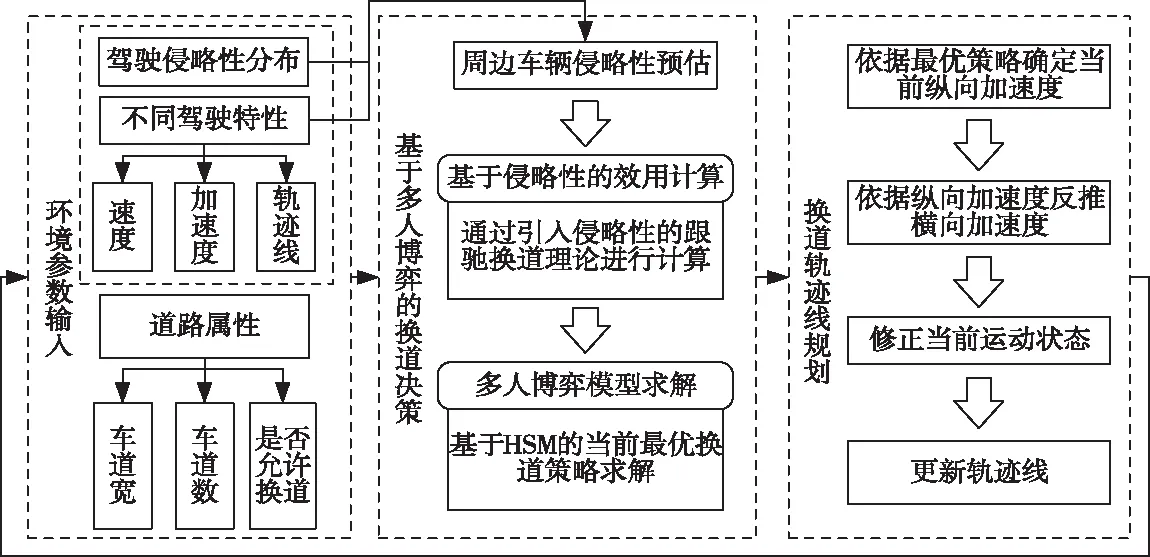
图2 模型算法逻辑图

3 模型建立与算法设计

3.1 基于NGSIM数组的驾驶侵略性分布估计

复杂车路环境下，换道过程会涉及到与周围多个车辆的交互，这需要对周围车辆的侵略性做准确估计。NGSIM数据组[16]包含了百万条车辆行驶记录，其十分适合用于车辆行驶特性以及自动驾驶仿真环搭建，本文主要以NGSIM为例，进行驾驶侵略性分布估计。

在NGSIM中选取若干条轨迹线，绘制图3所示速度随时间变化曲线。不难看出，由于驾驶员本身驾驶特性差异，在面对突发情况时，其选择的驾驶行为也是不同的，侵略性强的驾驶员，面对突发情况时往往会选择尽可能保持自己的空间与速度收益，而放弃安全性，反之亦然。

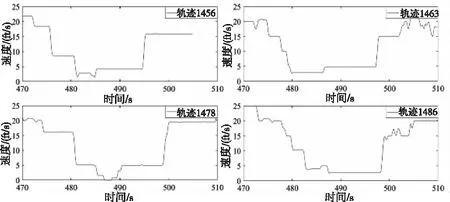
图3 NGSIM数据组中不同轨迹线

本文以车辆加速度绝对值大小(图3中曲线斜率绝对值大小)作为衡量侵略性的标准，加速度越大，驾驶员在行驶时往往会采取较为“冒进”的驾驶行为。将NGSIM加速度过大以及过小的数据进行剔除处理后，得到加速度分布情况。

数组中的加速度大小近似于对称分布，且最大值维持在11左右，最小值在-11左右。因此，本文侵略性对应的加速度应在-11到11之间。

3.2 基于多人动态博弈的换道决策

在复杂路况中，除去目标车道外，换道行为造成的横向偏移，会导致原车道的跟驰状态发生改变，后车会产生超车期望以获得空间收益。因此，需要对于后车的跟驰状态及其它重要参数与换道车辆横向偏移之间的关系做探究。

3.2.1 基于OEP的跟驰模型

部分研究探讨过横向偏移在跟驰模型中的影响。Jin和Wang[17]在Bando等人的OV模型[18]基础上，考虑了横向偏移对跟驰过程前车与再前车的影响，提出了非车道全速度差模型。

上述模型认为相同车辆的横向偏移对跟驰车辆的影响是相同的， 但实际上，由前车横向位置的不同形成的不同侧向净空宽度， 会对跟车的驾驶员及车辆产生不同的影响。基于此， 本文在OV 模型的基础上， 引入横向分离参数及超车期望与虚拟前车的概念来考虑车辆横向偏移对跟驰车辆的影响。

车辆跟驰模型不仅适用于当前车道上的车辆，也适用于目标车道上假定的跟驰车辆。车辆合并过程中，车辆在原车道上所留下的横向间隙称为通过间隙，其产生的超车期望定义为OEP。无论换道车辆前是否有车辆，原跟随车辆都会考虑在可通行的间隙前设置虚拟车辆，以确保安全。其逻辑示意如图4所示。

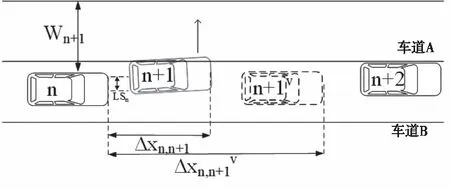
图4 OEP逻辑示意图

ΔXn，n+1为t时刻第n辆车与虚拟前车之间的车头间距，本文假设虚拟前车与跟驰车的间距是前车与跟驰车辆间的γ倍，γ越大，驾驶员所受影响越小，驾驶员所呈现的超车意愿越强。LSn表示跟驰车辆与前车的横向分离距离，Wn+1表示前车所给予的可超越间隙。

本文设车辆的超车期望为On以衡量超车期望对跟驰模型的影响，横向分离参数为当前车辆的横向分离距离与当前道路的最大分离距离的比值，定义为Pn。因为超车期望与前车的可超越间隙存在一点联系，故其存在以下几个特点：

G(Δvn，n+1(t)，Δvn，n+2(t))=(1-Pn)Δvn，n+1(t)+PnΔvn，n+2(t)

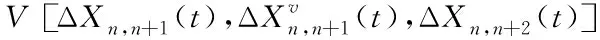
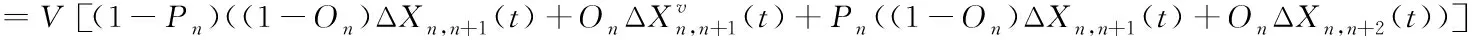
(1)

1)On随着前车的可超越间隙的增加而增大。

2)前车可超越间隙小于临界值时，默认为不存在超车可能，因此On的值为0。

3)当前车的可超越间隙大于或等于可通过间隙最大值时，认为此时超车期望达到最大值1。

基于以上建模思想， 建立模型微分方程：

其中，κ=驾驶员对速度差的敏感系数；ΔXn，n+1(t)=Xn+1(t)-Xn(t)=t时刻跟驰车n与前车的车头间距；V=t时刻跟驰车n与第二辆前车的车头间距；V=优化速度函数。

依据上述式子可得跟驰车辆的超车期望为

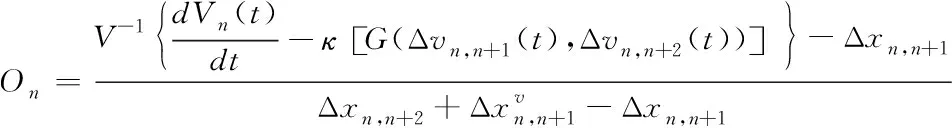
(2)

3.2.2 基于多人动态博弈的换道决策模型

在文献[19]的研究中，对于单一车辆换入车道的情况作了讨论，在其所提出的基于动态博弈论的基础之上，本文对于自动驾驶车辆换道在复杂车路环境下的换道决策搭建模型，主要的博弈关系表现如图5所示。

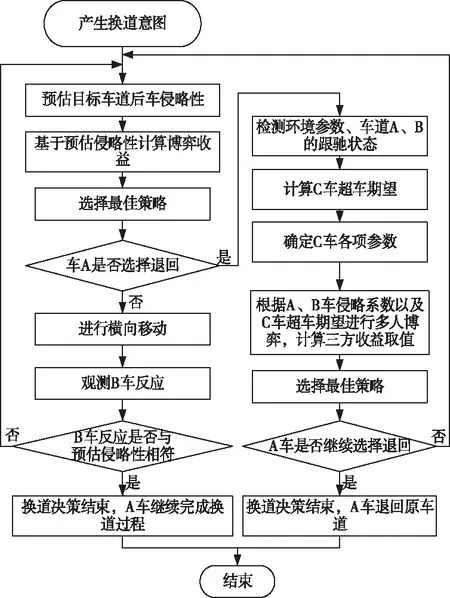
图5 基于多人动态博弈的算法框架

上述车辆编号参照图1(b)。博弈论模型的基本原理是计算博弈各方的收益函数，即需要准确求出A、B两车的收益。收益函数的计算依据文献[29]得到

Upayoff=fw(a，a0)((1-β(q))*Usafety(a)+β(q)*Uspace(a)+1)-1

(3)

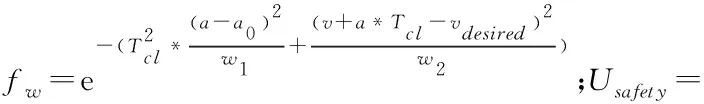
在引入超车期望前提下，则可以由此计算原车道车的效益，其计算公式如下

Upayoff=fw(a，a0)((1-On)*Usafety(a)+On*Uspace(a)+1)-1

(4)

其中，On=超车期望，0≤On≤1。

在文献[19]研究中，收益函数主要考虑车辆行驶的纵向加速度，而对于车辆的横向控制采用PID控制器进行模拟，车辆的横向运动几乎是线性的。为了更准确的模拟车辆换道过程，车辆的横向移动需要进一步标定。

3.3 换道轨迹线规划

基于已有的轨迹规划方法[20]，本文在其基础上采用多项式拟合方法进行轨迹线规划。

已知在车辆换道的初始时刻t0，车辆的状态为q0=[x0，vx0，ax0，y0，yy0，ay0]，分别表示x方向上的坐标、速度、加速度，y方向上的坐标、速度、加速度。换道结束的时刻为tn，该时刻下车辆的状态为qn=[xn，vxn，axn，yn，yyn，ayn]。车辆的换道轨迹函数可表示为

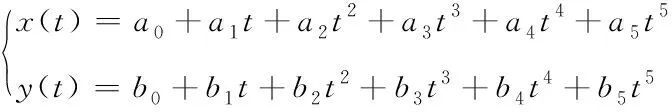
(5)

因为车辆换道时处于匀速运动，vx0=vxn=v，ax0=axn=0，车辆在换道开始与结束的时刻均与车道线保持平行，故ay0=ayn=0。

由以上公式可知，其结果取决于未知数tn，因此若确定未知数tn，则可表示多项式的各个系数，进而确定换道轨迹。

为避免车辆因侧向加速度过大导致侧滑或冲出路面边界线。设约束如下

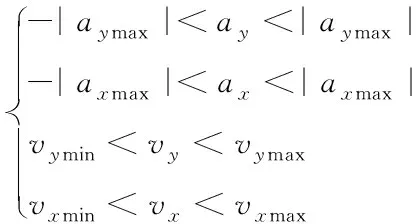
(6)

在换道过程中，车辆的侧向加速度与换道时间是关键因素，为保证车辆在安全换道的基础上，尽可能减少换道时间，设轨迹目标函数如下

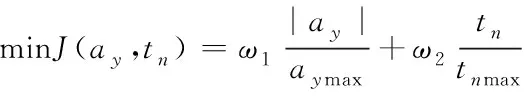
(7)

其中，ω1和ω2为权重系数，且ω1+ω2=1。

基于以上目标函数与约束条件，对车辆换道过程的轨迹进行规划，进而为车辆换道博弈提供支持。

3.4 多人博弈算法求解

从图5所示的算法流程来看，在自动驾驶车辆换道过程中若由于目标车道后车侵略性过大导致博弈失败，则会出现三方博弈的情况。本文将基于一种HSM算法[21]，对三方博弈的情况进行求解：

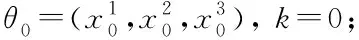
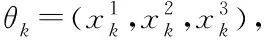
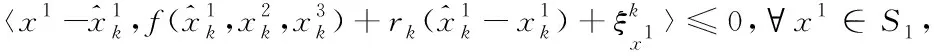
(8)

其中

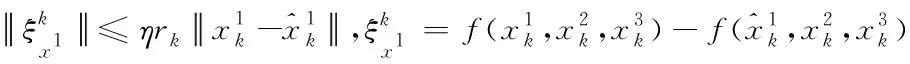
(9)

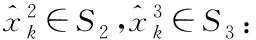
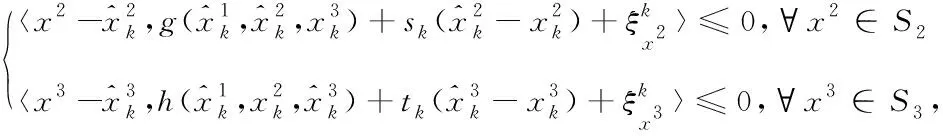
(10)

其中：a

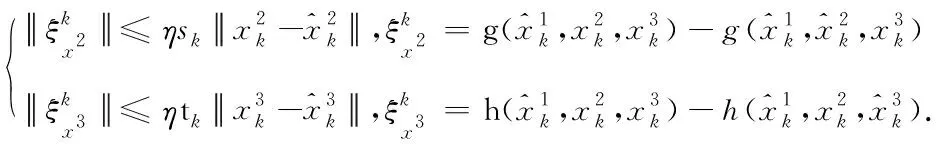
(11)

Step 4. 如果

(12)

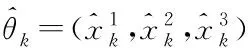
Step 5. 生成一个新的迭代点θk+1，

θk+1=θk-αkd(θk，k)

(13)

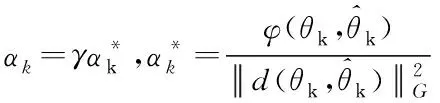
d(θk，k)

φ(θk，k)：=〈θk-k，Gd(θk，k)〉，

设k=k+1，返回step2。

整个换道博弈可以表示如下

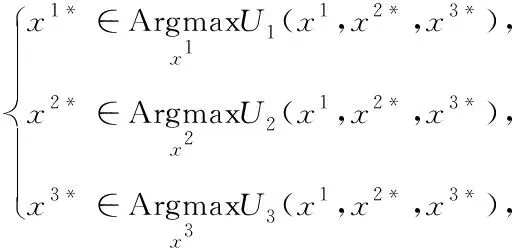
(14)

s.t.：

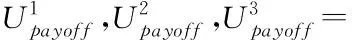
4 算法仿真与验证

4.1 仿真环境搭建及模型验证

在完成模型搭建及算法设计后，本文对该模型的有效性及适用性进行仿真验证，并采用NGSIM数据中的车辆轨迹线数据以及对应的道路参数进行仿真环境搭建。

本文选取的车辆样本如视频截图6所示。

图6 NGSIM采样视频图

图中，ID为1103的车辆(之后以ID简称车辆)处于一个慢车道上，由于左边车队1121与1119间隙较大，最理想的情况为换道进入快车道，但是由于1121的侵略性较强，1103换道失败，同时1096超车期望也较大，最终，1096选择下一个间隙换道。整个过程，两个车队系统都没有达到最优化，且1103很可能会与1121或1096产生冲突。因此本文将1103视为自动驾驶车辆，测试本文模型在此情况下的效果。

依照NGSIM数据，得到车辆初始参数如表1所示。车辆的字母编号参照图1(b)。为便于分析，以NGSIM中车辆1103(13.014，378.619)在3520帧的位置作为基准点进行标定。仿真环境参数按照NGSIM对应的实际环境参数进行设置(道路宽度，限速等)。为准确描述博弈过程中车辆的相互作用，对除A以外的车辆进行侵略性标定。由于A在本仿真中被视为自动驾驶车，故将其侵略性被设置为0.5。

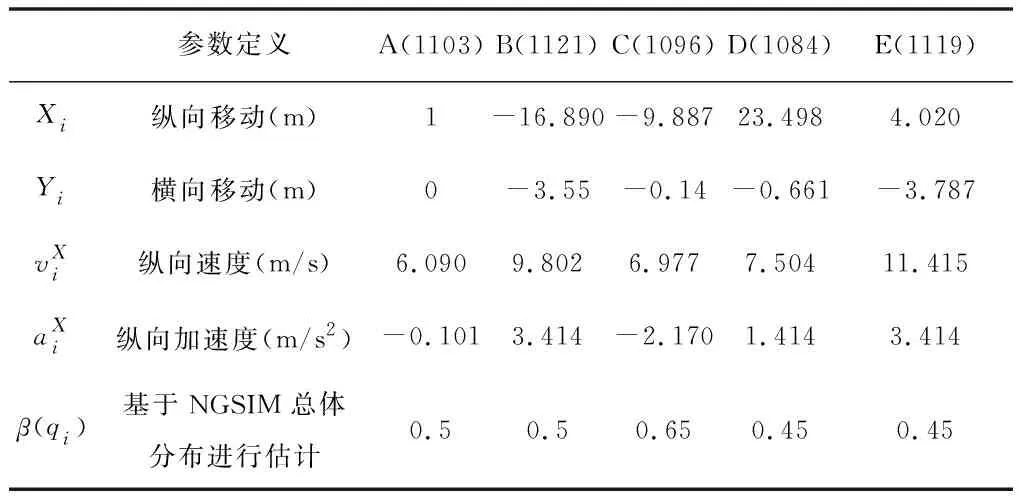
表1 初始仿真参数表

本次仿真利用MATLAB中Simulink套件进行。算法结构如图7所示。ACC决策模块负责博弈算法执行和轨迹线规划；车路环境模块负责仿真环境构建和参数的采集与输出；侵略性分布评估模块负责对驾驶环境中整体侵略性做预估；可视化模块在Simulink中现有的Bird’s-Eye Plot模块上稍作调整，负责整个仿真过程的可视化。

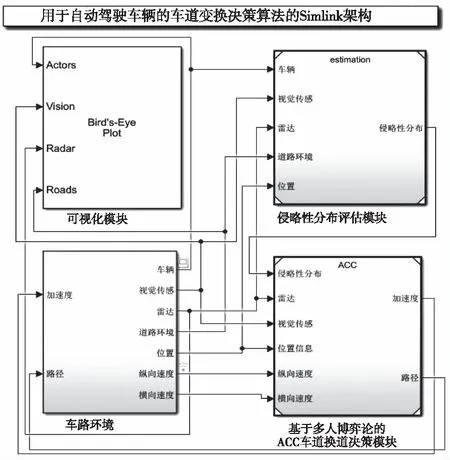
图7 Simulink仿真逻辑框架图

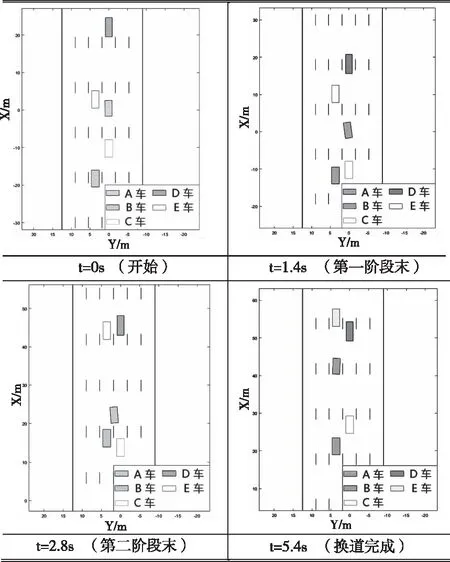
利用Simulink进行仿真，选出比较有代表性的几个时间节点的可视化结果，如表2所示。基于结果的具体分析见下节。

表2 仿真表

4.2 结果分析

依据仿真结果，车辆A在1.1s处产生换道意向，随后估计B车的侵略性，并试探性地侧移。在1.1-1.7s范围内，通过博弈计算，A车选择加速行驶。同时，随着A车横向偏移的增加，C车产生超车期望。1.7秒后，基于安全考虑，A选择减速退让。此时，C车与博弈模块进行交互，形成多人博弈模型。2.8秒时，在B与C的综合博弈中，车辆B选择避让，车辆A再次换车道直至换道完成。

该算法与传统的模型比较，更具适用性。文献[19]中的算法，A车难以在此情况下进行决策，B车会不进行避让，同时C车的超车期望会导致潜在冲突。仿真结果显示，由博弈模型使B车选择让步，A车成功改道，可见在此模型下，车辆A与车辆C之间的冲突得到了很好的解决。

为了更直观地显示在换道过程中车辆位置的动态关系，本文使用时空三维图展现车辆各时刻运动情况，如图8所示，每个小四边形的长度和宽度对应车辆的长度和宽度，如果图中四边形在同一时刻重合，则表示车辆发生碰撞。由图可见，在充分考虑轨迹线的动态决策下，各车之间保持了很好的间距，且线形十分理想。

图8 各车辆时间与位置3D示意图

另外，本研究中，除初始状态外，对结果影响最大的因素是目标车道后车辆的侵略性和原车道后车辆的超车期望。为更直观的比较不同参数的结果，将除了后车的侵略性外的初始输入参数值保持不变。将β(q3)初值设为0.65，步长为0.05，上限为0.9，下限为0.5。通过仿真研究中建立的模型和仿真环境，分析了不同β(q3)值的灵敏度。换道车辆轨迹图如图9所示。

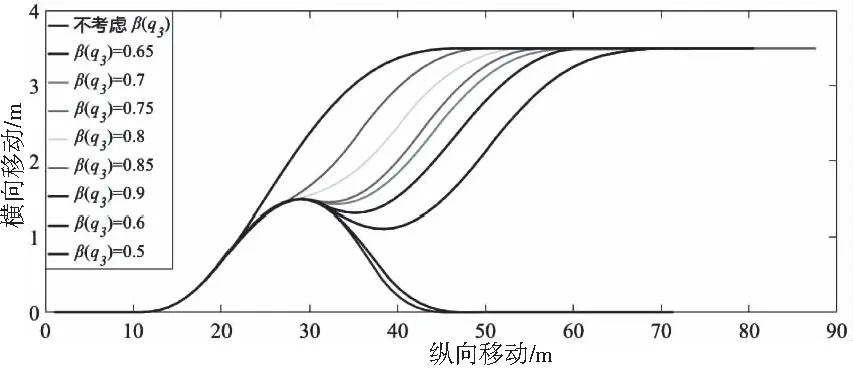
图9 不同β(q3)值换道车辆轨迹图

可以看出，随着侵略性的变化，车辆轨迹也发生了相应的变化。当β(q3)达到0.9时，第二阶段的博弈将在很短的时间内完成。当β(q3)降低时，超车期望的增加更依赖于后续车辆的相关参数。当β(q3)降至0.5时，第二阶段结束时，原车道后车的博弈失败，换道车辆在短时间移动后返回。通过计算换道车辆与相邻车辆在不同β(q3)值下的最小间隙，得到以下结果。

由表3可得，β(q3)去不同值时，该模型均可以得到合理的结果，表明了该模型可以很好应对不同侵略性的环境车辆下的换道决策，具有较强的适用性。

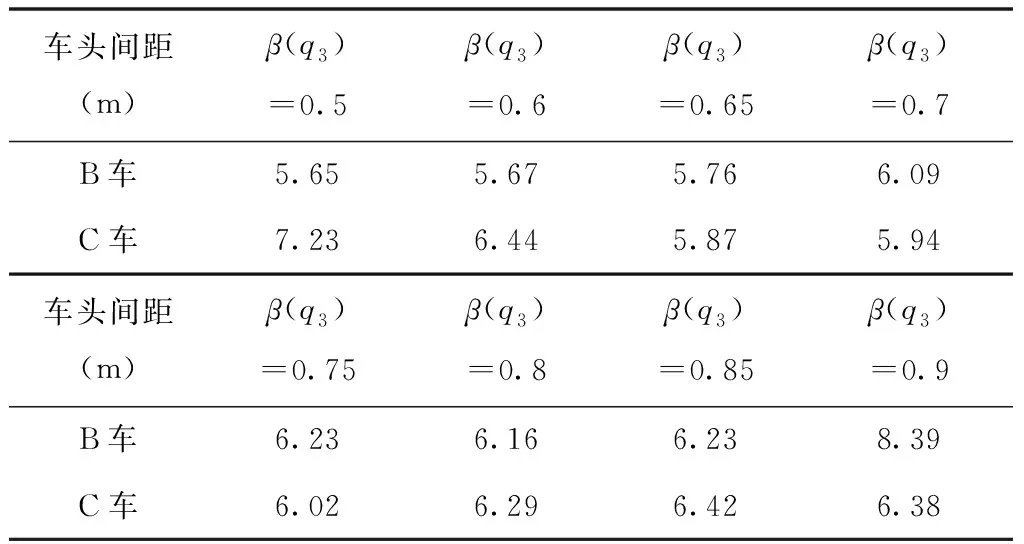
表3 不同β(q3)取值下的最小车头时距

5 结论

本文研究了自动驾驶车辆在复杂车路环境下的换道决策与轨迹线规划问题。提出了一种基于驾驶员整体侵略性的多人动态博弈变道模型。该模型以车辆整体轨迹线数据为驱动，不仅考虑了目标车道上的跟驰车辆侵略性，还综合考虑了周围环境车辆的行驶意图。仿真结果表明，本文设计的算法具有良好的性能和适用性，能够保证与人车交互时安全、高效地换道。

当然，本文算法是在NGSIM数据的基础上进行算法设计与仿真验证的，虽然NGSIM数据组已被众多论文证实具有较强的真实性，但本文模型的适用性还需要在现实环境中进一步探索和论证。此外，本研究只讨论直行路段的换道决策。当涉及到更复杂的道路线性如弯道时，算法的通用性需要进一步验证或增强。