基于CTM快速路事故下交通流牵制同步仿真
马小园,庞明宝*
(河北工业大学土木与交通学院,天津 300401)
1 引言
事故是造成城市道路交通网络偶发性拥堵从而降低其通行效率的主要原因之一,事故下控制是交通管理部门的核心工作,特别是通勤等需求较高时段的城市快速路,其相对封闭性使事故处理难度加大,事故影响程度更严重[1,2]。考虑到快速路相邻匝道间距离较短,单匝道调节和主线限速效果有限,事故下的多匝道协调控制已成为主要手段。现有研究已证明其有效性[1,2],但集中于协调控制算法方面[1],较少涉及协调控制信号施加策略方面[2],如栾燕海等[2]建立城市快速路主线和多匝道协调控制元胞自动机模型,分析不同需求下采取多种信号控制对交通流所造成的影响。但不涉及复杂网络牵制同步和元胞传输模型(cell transmission model,CTM)。
CTM能兼顾元胞自动机和宏观模型的优点,清晰地再现车辆排队的物理现象、映射出大规模路网的动力学等特性,近年来成为研究交通问题的重要仿真工具。如肖恢翚[3]等基于交通流特性提出事故下改进CTM。这些为事故下城市快速路管控研究的进一步深入提供了基础,但不涉及复杂网络同步。
采用复杂网络理论方法研究道路交通复杂网络系统是一个新课题,集中在三个方面:①城市道路交通的复杂网络拓扑结构、动态演化机制等[4]。②城市交通网络级联失效问题[5]。以上两个方面均不涉及具体控制器设计,也不针对城市快速路。③交通管理控制问题;如基于CTM建立城市快速路节点耦合模型,设计牵制控制器,达到以“较小控制范围促使系统稳定”的目的[6],但面向一般拥堵不涉及事故下。
目前采用复杂网络牵制同步思想对城市快速路突发交通事故的协调控制研究较少,针对事故下交通流状态变化,确定最佳信号施加策略,使事故下的交通流快速趋于稳定状态是本研究的目的。基于此,本文以事故下城市快速路交通流为研究对象,基于CTM对事故点上下游路段重新划分,重构节点,修正事故下节点耦合模型,以牵制同步为目标设计协调控制器,通过具体仿真予以验证。
2 快速路事故下节点耦合仿真模型
2.1 事故路段改进CTM
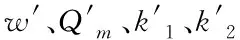
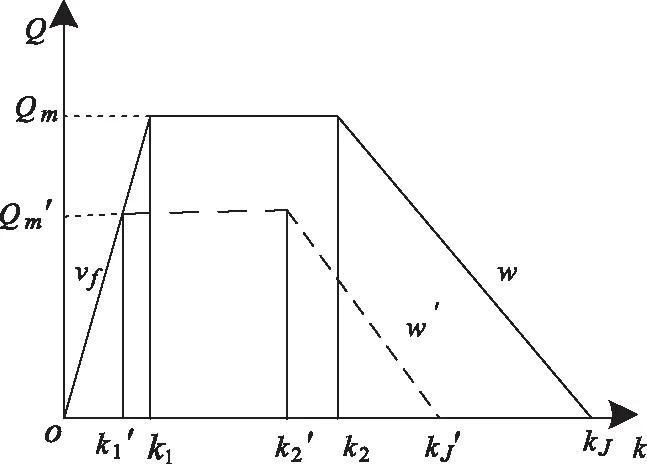
图1 事故与非事故下流量-密度关系图
由离散化流量守恒得t+1时元胞m的流量为
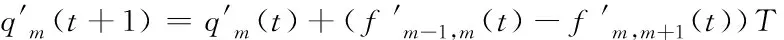
(1)
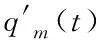
由图1可将事故路段的流量传输关系调整为
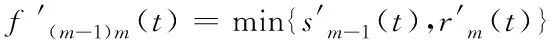
(2)
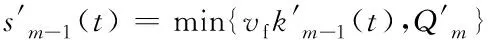
(3)
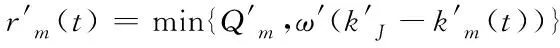
(4)
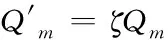
(5)
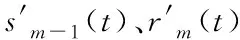
2.2 重划事故点上下游元胞
考虑到事故发生的随机性及图1所示事故路段与非事故路段的交通流特性差异,一旦发生事故,需对事故点上下游路段进行元胞重新划分,以保证“事故路段用调整后的CTM,其它路段依然采用原CTM”来映射。假定事故发生位置(事故点)位于原元胞m边界内(见图2),以事故点为分界点,且最多跨越2个元胞即原元胞m和m-1(考虑到快速路大部分为小事故,事故路段一般较短);事故点距离原元胞m最上游边界处长度为l1,事故点距离原元胞m最下游边界处长度为l2,重新划分的元胞应使得事故点始终处于元胞的最下游边界处,具体为:
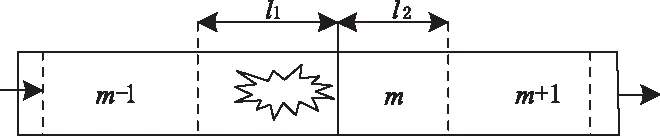
图2 位于元胞边界内的事故点(表示事故点)
1)若事故点恰好处于原元胞m最下游边界处,此时原元胞划分无需改变。
2)若l1≥vfT,即事故路段在原元胞m内,则将原元胞m最上游边界处到事故点的这一路段设置为新元胞m;若l2≥vfT,则将事故点到原元胞m最下游边界处这一路段设置为新元m+1。
3)若l1≥vfT,即事故路段在原元胞m内,则将原元胞m最上游边界处到事故点间这一路段设置为新元胞m;若l2 4)若l1 5)若l1 将快速路抽象为由N个节点及关系组成的系统,定义标准节点[5]如图3所示的由一个主线元胞、一个出口元胞和一个入口元胞组成[5],非标准节点均有一个主线元胞,对没有出口匝道或入口匝道、或都没有,该部分流量设置为0。事故下,由于原元胞重新划分,需对对应节点进行重构,具体为: 图3 快速路标准节点 1)若原元胞没有重划,则对应节点无需重构。 节点i的状态方程为 (6) (7) (8) 2)若原元胞m被划分为两个新元胞,则分别将这两个元胞所在路段重构为两个独立节点i和i+1,其中节点i只包含一个入口匝道p,节点i+1只包含一个出口匝道o。 3)若将事故点与原元胞m+1最下游边界处重新划分为元胞m+1,则将该路段重构为独立节点i+1,该节点增加一个出口匝道。 4)若事故路段跨越2个元胞且事故点与原元胞m-1最上游边界处划分为新元胞m-1,则将该路段重构为独立节点i-1,该节点增加一个入口匝道。 5)若事故路段跨越2个元胞且原元胞m被划分为两部分并分别与原上下游元胞重组为新元胞,则将新元胞所在路段重构为独立节点i-1和i,这两个节点分别增加一个入口匝道和一个出口匝道。 (9) (10) 当产生拥挤的节点以ω′反向传播时 (11) (12) 事故下节点耦合模型为 (13) (14) (15) (16) (17) 将城市快速路系统稳定到同步状态[8],即t→∞时,k1(t),k2(t),…,kN(t)→kd(kd为期望密度),满足以下条件 f(k(t))=kd (18) 为达同步目标,需对含有入口匝道的“事故点及上游最近的c个节点(牵制节点数)”施加匝道调节信号,节点状态方程为: (19) 式中:ui(t)为节点i的密度调整值,通过入口匝道调节实现。计算见下式 ui(t)=-aiidi(ki(t)-kd) (20) 当i=1,2,…,c时,反馈增di>0;i=c+1,c+2,…,N时,di=0。 依据系统稳定性条件[5,7],当满足下式时系统达到稳定 (21) 显然有合适的θ值在G′、A和c已知情况下,可得到优化的反馈增益矩阵D。步骤: 1)寻找到合适的θ和G′、A初值。 2)设置c=1。 3)对给定的c值,依据式(21),看是否能够计算得到D。若能,则输出最优c和D;若不能且c 4)令c=c+1,转向3)。 5)修改θ和G′、A值,转向2)。 当城市快速路主线元胞突发交通事故并造成拥堵时,必须采取相应控制措施以抑制拥堵扩散。文献[5]中采用的牵制控制方法能够达到快速路系统有效抑制交通拥堵的目的,这与事故处理的目标一致,因而,本研究在此基础上结合事故条件下快速路的交通流特性提出事故下快速路的控制策略,见图4。 图4 城市快速路牵制同步策略 控制策略步骤为: 1)采用信息采集子系统和事故诊断分析子系统实时识别快速路状态。 2)如果有节点k>kd且没有事故时,转向3);当出现事故时,转向4);否则,系统处于自由流状态,不输入任何匝道调节信号,转向1)。 3)按照一般交通拥堵[5],确定最优c和D,输入到快速路系统,转向6)。 4)采用事故诊断分析子系统等确认事故路段长度、所占车道数等信息,元胞重划、节点重构、调整节点耦合模型。 5)采用2.2节方法确定事故下最优c和D。 6)若c=0则不施加匝道调节信号,系统处于自组织状态,转向1);否则转向7)。 7)若c=1为单匝道调节;若c=N则为全局多匝道协调控制;否则为部分匝道协调控制。 8)将最优c和D输入快速路系统中,转向1)。 选取天津市快速路南半环逆时针方向“红旗南路宾悦桥-黑牛城道海津大桥与昆仑路交点”段为实验对象,经调查该段快速路的设计指标和参数:单向四车道,长10.89km,10个入口匝道、9个出口匝道和3座立交桥, Qm=1950veh/(km·lane),vf=65km/h, kJ=130veh/(km·lane)(后同)。从上游到下游划分为非事故下节点10个并建立CTM,主线元胞长度(km)分别为0.74、1.80、0.73、1.00、1.10、0.95、1.70、1.20、0.67、1.00。修正后参数为(略): k1=30, k2=61, kd=45, α=0.25, β=0.21。 选取上午7:00-8:00为实验时间段,T=10s,同时为进行对比分析,本实验暂不考虑入口匝道排队长度限制。图5为某个工作日7:03于节点8主线元胞距下游边界180m处发生事故(事故占用单车道且延迟时间为20min)不控制(No-control Signal, NCS)时仿真的各节点密度变化:节点8密度迅速上升达到78.26veh/(km·lane),并迅速向上游节点蔓延,造成大范围拥堵,同时还引发入口匝道产生排队现象,节点7尤为明显。 图5 NCS下密度及入口匝道排队长度变化图 若采用本研究牵制同步方法(Pinning Control Signal,PCS)仿真,先对事故路段上下游节点进行重新划分,其中事故点距上游边界处的长度为1.02km,满足2.2节所述情况(3)。取θ=0.999得c=4,控制范围是节点8到5;反馈增益D=[0, 0, 0, 0, 17.92, 14.74, 27.16, 16.78, 0, 0],以此为控制器参数进行仿真。图6为各节点密度与入口匝道排队长度变化。 图6 PCS下密度及入口匝道排队长度变化图 由图5-6可以看出: 1)采用本PCS方法,150s后节点7密度趋于期望值,拥堵得以最大限度抑制;TTT由730 491s降低到620 680s,流量由19 840veh增加到213 88veh,平均排队长度由34降低到21veh。这是因为事故下采用本方法进行入口匝道调节使得系统有序,在受事故影响的路段处于期望密度状态时,流量趋于较高水平,匝道平均排队长度有所降低,城市快速路的通行效率得以提高,从而初步验证了本方法的有效性。 2)匝道最大排队长度由218veh增加到242veh。这是因本方法对事故点匝道进行调节所造成的,虽然带来了社会不公平性,但为实现系统最优必须付出相应代价。 3)GCS各指标同样达到抑制拥堵提高道路通行效率的目的,但控制效果稍差于PCS方法,这是因在本例中,距离事故点较远路段,不需要匝道调节,若进行则造成这些路段的匝道用户进入主线时间延长,TTT增加、流量减少,同时也造成了社会不公平性,从而进一步验证了本牵制同步的有效性。 图7-8分别为TTT与拥堵影响长度L(Length)随事故持续时间的变化曲线图;各控制效果指标比较见表1。 图7 TTT变化曲线 图8 拥堵影响长度变化曲线 表1 不同控制方式下各指标比较 表中各指标:总旅行时间TTT(Total Travel Time)[9]、匝道平均排队长度AQL、匝道最大排队长度MQL;GCS(Global Control Signal)为全局同步,即采用2节同样方式但需对全部匝道施加调节信号,计算得到D=[5.52, 14.86, 5.43, 7.81, 8.69, 7.37, 13.98, 7.99, 6.49,7.81]。 图7-8可以看出: 1)随着持续时间的增加, TTT和拥堵影响长度均有所增加,但与NCS相比,采取PCS后, TTT和拥堵影响长度明显低于NCS下;同时与快速路系统在NCS下的自组织相比,采取PCS方法能快速 缩短系统达到稳定状态的时间,使事故下的交通流逐步从无序状态恢复到有序状态。 2)NCS下TTT增加到730 491s,本PCS方法增加到620 680s,出行者的总旅行时间缩短了109 811s;NCS下拥堵影响长度增加到5.02km,本PCS方法增加到2km,拥堵路段长度明显减少,拥堵范围得以控制;进从而一步验证了本PCS的有效性。 3)考虑到事故条件下的持续时间、车流量等各项指标均与非事故下的状态有较大差距,如TTT增加等,因而应及时采取交通事故管理措施对事故进行处理并确定拥堵节点,对其所处路段施加信号调节方案进而实现多匝道协调控制,以最大限度减少事故给交通网络所造成的影响。 1) 以城市快速路事故路段的基本图变化为出发点,建立了多入口匝道协调控制方法,对路段下游发生单车道事故施加不同的控制信号,对其进行仿真,得到最优控制策略。 2) 本研究只是初步研究,尚需在事故发生在不同位置(出入口匝道、交织区等)、不同交通需求、事故占用不同道路长度以及不同节点发生事故造成的多节点拥堵等问题进行研究。2.3 建立节点交通流仿真模型
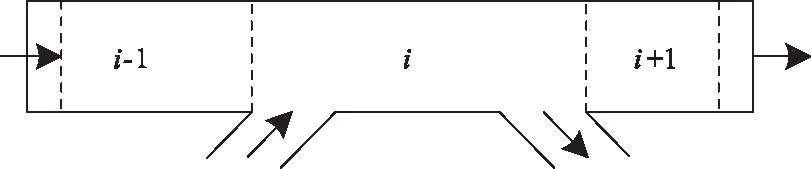
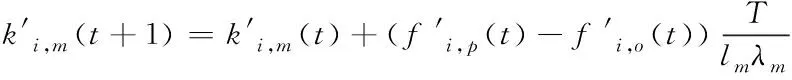
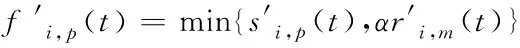
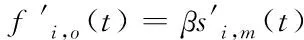
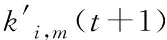
2.4 修正节点耦合仿真模型
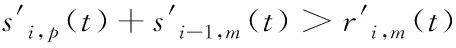
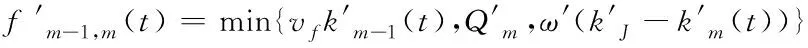
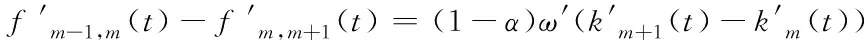
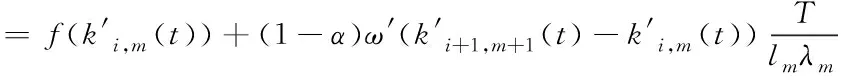
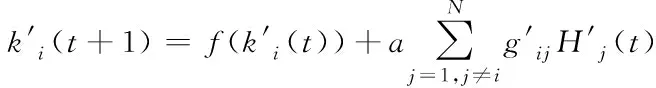
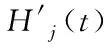
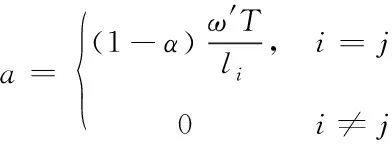
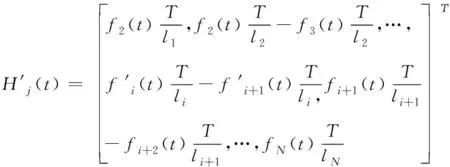
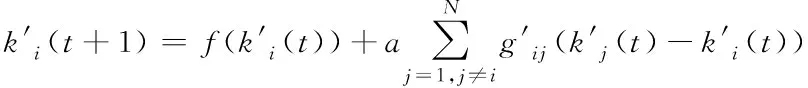
3 事故下快速路牵制同步控制器设计
3.1 控制器算法
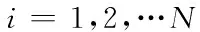
3.2 牵制节点和反馈增益优化
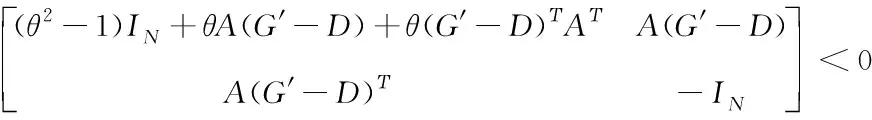
3.3 控制策略
4 实验分析
4.1 实验对象
4.2 仿真计算及控制效果分析
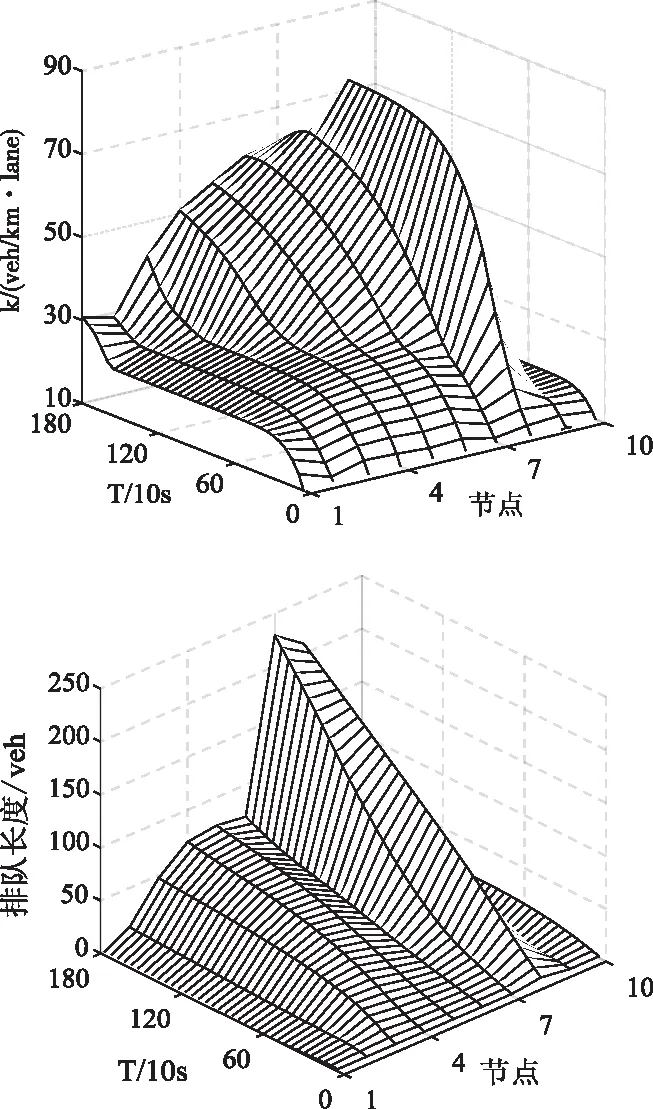
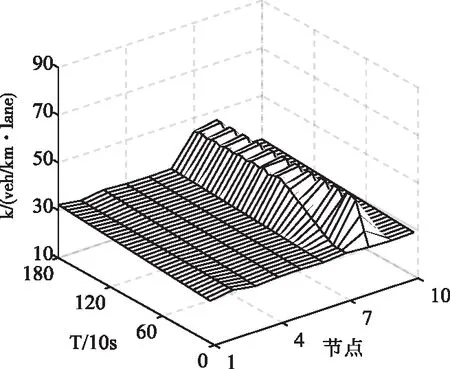
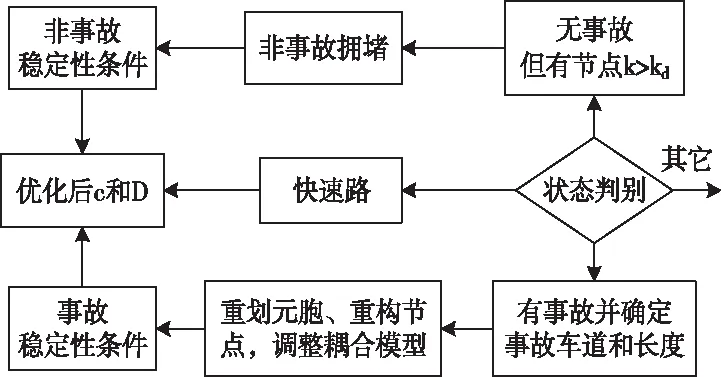
4.3 事故参数对控制效果影响分析
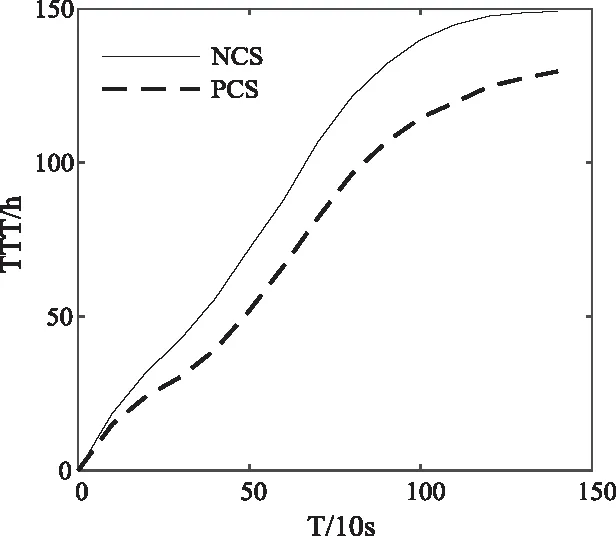
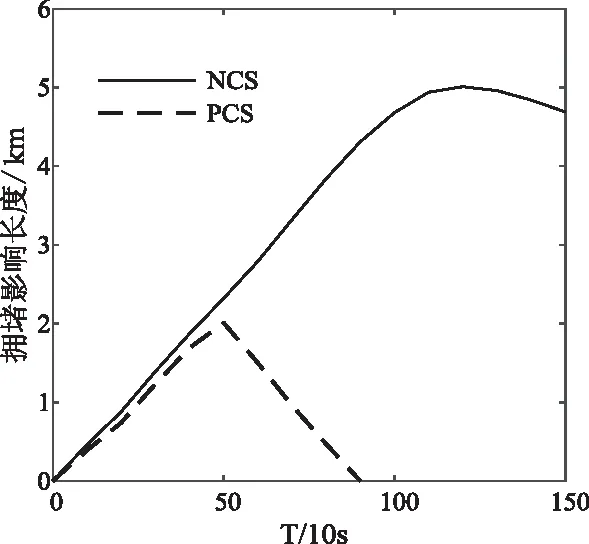
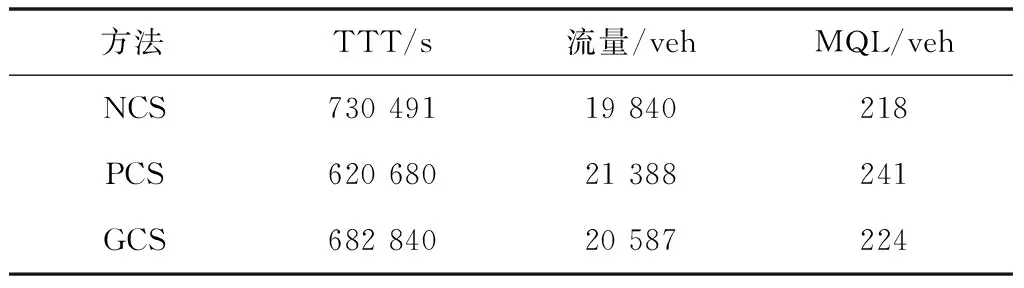
5 结论

