基于模糊积分的多载波通信信号盲识别算法
王 涛,耿 鹏
(中国人民解放军第91998部队,辽宁 大连 116000)
1 引言
无线通信系统中的数据、视频、图像等高质量多媒体日益发展,使无线通信方式成为了通信发展的主要趋势,对多载波通信信号的识别也成为了研究焦点。载波即为载着数据的特定频率无线电波,通常情况下,无线通信传输的数据频率是低频的,如果根据数据本身频率进行传输不利于数据接收和同步。单载波的通信系统信号带宽要小于信道相干带宽,其接收端符号间的干扰不严重,只需要使用简单的均衡器即可消除干扰项,但是随着数据传输速率的不断提高,信号的带宽比信道相干带宽要大,使用简单均衡器无法有效地消除干扰,此时可以通过多载波系统将高速的串行数据流转换为低速并行的数据流,同时调制多个载波使信道时延扩展,以减小干扰。多载波的抗干扰能力更强,频谱利用率更高,在通信系统的应用中具有一定优势。
姚宇晨等人[1]提出了一种基于深度学习的通信信号自动调制识别技术。该方法首先通过自编码技术对信号进行特征提取,得到抗干扰能力较好的特征集,随后采用BP神经网络对获取的特征集进行分类识别,完成通信信号的自动识别。在仿真条件下证明该方法的分类识别的效果较好,能够有效地提高调制信号识别的抗干扰能力,但是识别过程较为复杂导致识别效率较低。徐茂等人[2]提出了一种基于通信信号时频特性的卷积神经网络调制识别。该方法首先收集数量较多的调制信号,通过短时傅里叶变换将信号的时频特征转换为图像特征,并将图像特征作为网络输入,得出一种具有参数较少的卷积神经网络,然后通过改进神经网络中不同层的连接方式提高特征提取能力,最后为防止模型出现过拟合问题,增加模型的稳定性,在网络中加入归一化层完成识别全过程。实验表明该方法的参数和训练时间较少,且准确率较高,但是识别效果不佳。
针对多载波通信信号特征,提出一种基于模糊积分的多载波通信信号盲识别算法。模糊积分为一种能够对多源信息进行处理的有效方法,为使模糊测度更适用于多波载通信信号识别,给出两个相关定义,然后通过对多载波的不同信号构造矩阵计算出矩阵的奇异值,并使用归一化处理和降序排序处理方法去除干扰值,最后使用模糊积分确定较大奇异值个数,根据相关评判标准完成识别全过程。
2 多载波通信信号预处理
模糊积分为一种能够对多源信息进行有效处理的方法,模糊测度[3]能够表示位置未定元素从属于该集合的信任度,其属于经典概率测度的推广,但是模糊测度并不具有可列可加特性,为了使其更适用于多波载通信信号识别,对其进行改进,给出如下定义:
定义1:设X表示某一论域,X={xi},φ(X)表示X的幂集合,设A、B为集合中任意元素A,B∈φ(X),当λ>-1时,gλ为模糊测度,在此条件下gλ具有如下特性
gλ(A∪B)=

(1)
当gλ满足A,B⊂X,A∩B=Φ时,恒有:gλ(A∪B)=gλ(A)+gλ(B)+λ·gλ(A)·gλ(B)。则当λ>-1时,模糊测度具有可列可加特性,模糊测度是gλ测度的一个特例。
模糊积分是一种基于gλ模糊测度的非线性运算[4],令M为X上的模糊测度,h为X上的模糊集合[5],A是X的子集合,Ai={x1,x2,…,xi}。假设h(x1)≥h(x2)≥…≥h(xn),则A的模糊积分可以表示为

(2)
设gi∈[0,1],令gi=gλ({xi})(i≤n),则可得
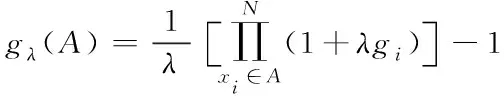
(3)
式中,gi为模糊密度,当以gλ模糊测度来计算模糊积分时,则第i个密度值gi可以解释为信息xi的输出置信度。
λ值的求解为模糊积分计算[6]过程中尤为重要的环节,可以通过如下方程进行求解
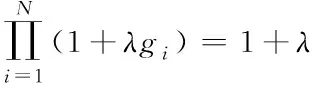
(4)
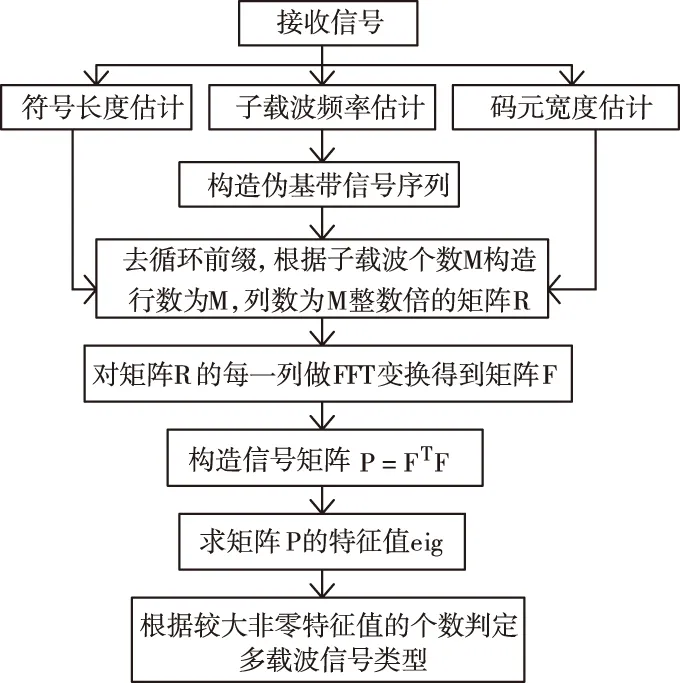
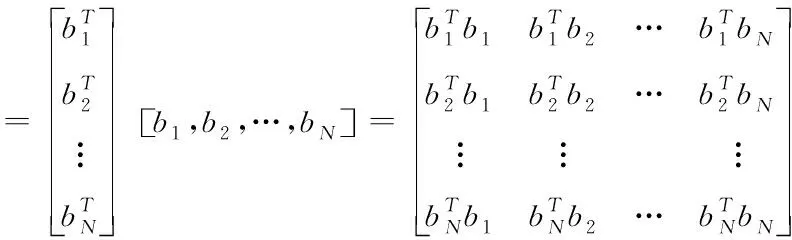
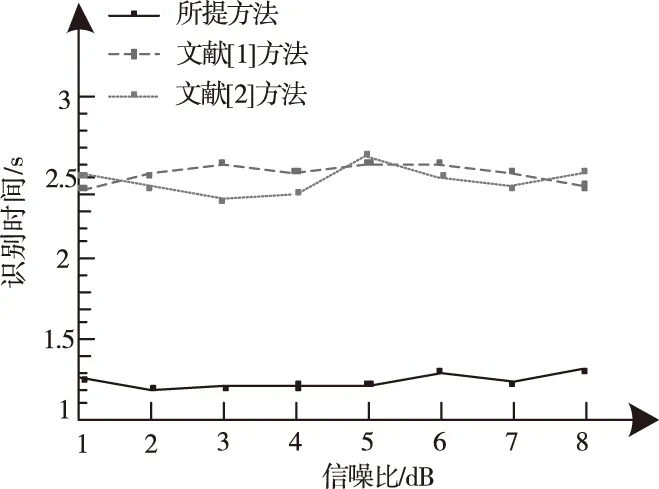
求解后得到λ∈((-1,0)∪(0,+∞))。式(4)为一个多项式求根过程,当n<3时,可直接使用代数方法求取f(λ)=0的根。当n≥3时,使用代数求解较为困难,可以采用数值法进行求解,即定义任意固定集合{gi},gi∈[0,1],1 (5) 式中,函数f′(λk)的求解方法如下 (6) 使用牛顿法对λ值进行求解需要解决函数f(λk)的导数值计算问题,因此为便于描述以上问题给出定义2。 定义2:若算子Δ为某集合G内任意相异元素之间的乘积和,则对于集合G={gi,g2,…,gn}有 (7) 则有 +g2g3+g2g4+…+g2gn+…+gn-1gn; (8) 由算子Δ表示的f(λk)如下 (9) (10) (11) 从式(11)中可以看出,该计算过程较为复杂,难以满足实时性要求。因此,为了提升识别速度,给出了如下f(λk)的简洁求值方法。 使用机械求解法结合牛顿法即可简化求解过程,提高求解速度,并且由于其存在规律性,求解释时不必将其展开为规范的多项式。 对f(λk)直接计算时,每进行一步迭代,实际的计算量为2n-1次,其中求解各因式λgi的乘法运算计算量为n次,随后的n个因式相乘还需要进行n-1次计算。 f′(λk)的计算则可以在f(λk)求导后代人λ=λk获得,其表达式如下 (12) 通过以上方法进行实际计算时,f′(λk)可以通过对f(λk)计算的中间结果共享大大减少计算量,提高计算速度。 多载波的平均频率相对来说可以低一些,但多载波的最高频率与单载波的频率相对来说,并不会相差很大。载波频率[8]的最大好处就是可以降低信号传输过程中的多径反射干扰(即图像重影效应)。多载波通信信号盲识别算法流程图如图1所示。 图1 多载波通信信号盲识别流程 图1中4种信号分别为OFDM信号、MC-CDMA信号、MC-DS-CDMA信号和MT-CDMA信号,在对4种信号矩阵的构造过程中,OFDM信号和其它3种信号的构造方式稍有不同,主要是由于其数据矩阵内不包括扩频码。 对于OFDM信号,去循环前缀后构造接收矩阵ROF=B=[b1,b2,…bN],其中N=1,2,…,N表示实数和复数组成的M×1维列向量,N=kM,k≥2,根据ROF=BTB可得N×N维矩阵如下 (13) 通过对矩阵元素分析可得,OFDM信号各个子载波的信道情况不同[9],采用的调制方式也不同,使得该矩阵为由实数据与复数据同时构成的非零对称方阵,并且信号在各子载波上传输时通过不同方式产生的数据不同[10],因此,不同时刻各个子载波上传输数据所构成的向量线性不相关,即矩阵B为行满秩矩阵,若B的秩rank(B)=r,则r=M。根据矩阵秩的特性可知,矩阵POF的秩rank(POF)=rank(B)=r=M,即对POF进行奇异值分解时,能够获得r=M个非零奇异值。 对于MC-CDMA信号,有 RMC=E=cTa (14) 式中,c=[c1,c2,…,cM]表示长度为M的单项扩频码序列;a=[a1,a2,…aN]表示恢复的带有原始信号信息的数据序列,则根据式(14)可以构造矩阵如式(15)所示。 PMC=ETE =(cTa)TcTa=aTccTa=aT[c1,c2,…,cM] (15) (16) 矩阵E各列与扩频码构成的列向量按照数据序列数值成比例,即矩阵E的列向量呈两两线性相关,因此,可以得出E的秩rank(E)=1。根据矩阵秩的特征可得rank(PMC)=rank(ETE)=rank(E)=1,因此,对矩阵PMC进行奇异值分解时,只有1个非零奇异值,这是MC-CDMA信号矩阵与其它多载波通信信号构造矩阵的不同之处[11,12]。 对于MC-DS-CDMA信号和MT-CDMA信号,根据二者的构成特点得到矩阵RMD、RMT的数学表达式如下 (17) (18) (19) (20) 两种信号构造的矩阵形式大致相同,并且PMD是PMT的特例,因此以PMT为例,证明矩阵秩的特点。 根据以上特点对多载波通信信号进行识别,由于噪声等影响因素产生的非零奇异值比信号产生的非零奇异值要小,所以为除去干扰值,使用归一化处理和降序排序对非零奇异值进行处理,然后对非零奇异值序列作差分处理获得梯度序列,寻找最大峰值位置,使用模糊积分确定较大奇异值个数,若得到的奇异值个数为M个,则判定其为OFDM信号,若奇异值个数为1,则判定为OFDM信号,若为N/M个则为MC-DS-CDMA信号,如果奇异值的数量均不是以上数值,则判定其为MT-CDMA信号。 为验证所提方法的有效性,对不同类型的载波通信信号进行仿真。 实验中选取的载波信号分别是上文中提到的OFDM、MC-CDM、MC-DS-CDMA和MT-CDMA4种信号,4种信号的子载波个数均为16,MC-CDMA信号和MC-DS-CDMA信号的扩频码为长度是16的Walsh序列,MT-CDMA信号的扩频码为长度是63的Walsh序列,信号的循环前缀时长为信号时长的四分之一,基带数字序列为矩形脉冲成型,信号载频为50MHz,采样频率为200MHz,升余弦窗的滚降系数为0.1,对各个数据窗函数的残留数据进行叠加。 在无载波频率偏移的条件下,M和N的值分别取16和128,进行50次仿真识别实验,平均识别率随信噪比的变化情况如图2所示。 图2 多载波信号平均识别率 从图2中可以看出,4种信号中除了OFDM信号的平均识别率稍低之外,其它3种信号的平均识别率均保持在较高的水平,且不易受信噪比的影响。当信噪比达到10dB以后,4种信号的识别率明显下降,主要是由信号结构和扩频码长度导致的。综上所述,所提方法能够有效地识别出多载波通信信号,并且准确性较高。 为了进一步验证所提方法的应用效果,以识别效率为实验指标,对比基于深度学习的通信信号自动调制识别方法(文献[1]方法)和基于通信信号时频特性的卷积神经网络调制识别方法(文献[2]方法)与所提方法对多载波通信信号的识别效果,具体结果如图3所示。 图3 不同方法的信号识别效率对比 分析图3可知,采用所提方法对多载波通信信号进行盲识别时,识别时间始终低于1.5s,而文献[1]方法和文献[2]方法的识别时间均在2.3s以上,明显高于现有方法。说明所提方法可以对通信信号实现快速识别,识别效率更高。这是由于该方法在求解过程中,使用机械求解法结合牛顿法简化了求解过程,提高了求解速度,从而提升了多载波通信信号的识别效率。 将模糊测度、模糊积分等理论应用于多载波信号盲识别中,提出了一种基于模糊积分的多载波通信信号盲识别算法。仿真证明了该方法的可行性和准确性。总结全文的创新点如下: 1)对模糊测度重新定义,在使用牛顿迭代求解模糊测度中的λ值时,由于计算复杂度高,不宜采用直接展开的方式对多项式求根,本文通过对方程变形后,直接代入数据求解,该方法的求解方法简洁明了,使计算的复杂度大大降低,并且能够给模糊积分融合、决策和控制等其它领域的λ值计算提供参考。 2)避免了传统识别算法在特征提取后设计分类器的繁琐过程,简化了识别流程,并且算法中信号构造矩阵阶数N值的选取过程不必遵守与子载波个数整数倍的关系,所以可选取较小N值,减少运算量。
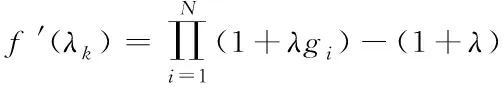
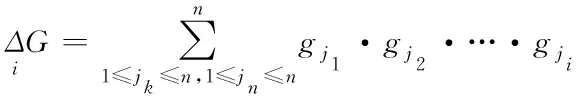

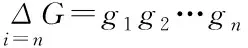
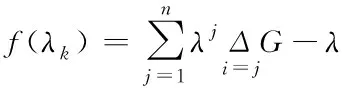
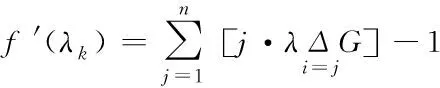
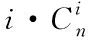
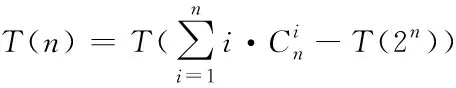
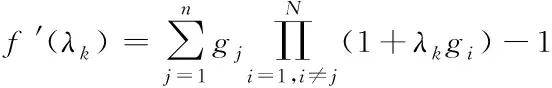
3 多载波通信信号盲识别算法


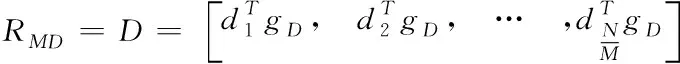


4 仿真研究
4.1 多载波信号参数设置
4.2 实验结果分析

5 结论

