基于时延特性的短时动态交通流预测模型研究

温惠英，曹 正

(华南理工大学土木与交通学院，广东 广州510641)

1 引言

跟随不断加快的城市化进程，城市道路交通压力也不断增加，随之而来的是不断升高的交通需求。缓解城市交通压力的一种有效解决方法是实现交通信号的主动控制，其核心是实现交通路网的短时动态交通流预测[1-3]。对于交通管理方面而言，通过短时动态交通流预测能够及时且主动地按需分配路网时间与空间资源，使交通出行效率与路网运行稳定性得到提高；对于出行者而言，以短时动态交通流预测为车辆路径规划的参照，可以有效帮助出行者规划更优路径，可以节省时间，使出行更加便捷。

然而，交通流运行的复杂性与不确定性较为明显，难以轻易获得准确的短时动态交通流预测结果。为此，相关专家学者对此展开研究并建立相关的交通流预测模型，但大多都没有充分利用除目标路段之外其它相关路段的交通流信息，也没有充分提取交通流传输特性参数，一定程度上导致预测结果的可靠性受到影响[4，5]。

针对这一问题，钟颖[6]等人研究了基于XGBoost的短时交通流预测模型，通过XGBoost 实现交通流量预测，但其建模时只考虑了当前断面的交通流特性，不同断面间的关联信息被忽略，构建的模型不具备较好的鲁棒性，容易被噪声干扰。高洪波[7]等人研究了基于分形与三次指数平滑的交通流量预测模型，其网络输入是表征路网结构的空间信息与历史事件信息，利用所分析的数据时空特征与不同断面时刻的数据相融合，但其没有注意到不同断面流量之间的时延特性，导致时间与空间上的流量数据相似度较低。

针对传统预测模型存在的不足，本研究基于时延特性构建了新的短时动态交通流预测模型。该模型通过干道流量关键点以及路网相关联断面数据，使模型采集到的信息更丰富，并通过相似性度量时间与空间维度上的数据段，融合不同断面数据，通过对不同断面历史数据中有效信息的挖掘，实现短时动态交通流预测精度的提高。

2 短时动态交通流预测模型设计

2.1 交通流时间序列相空间重构

相空间重构是一种非线性建模方法，它是动力系统方法对非线性时间序列展开分析的前提。

设置单变量时间序列为

{x(t)|t=1，2，…，N}

(1)

通过延迟坐标状态相空间重构法能够得出延迟矢量以及轨迹矩阵为

(2)

其中，m、τ分别表示嵌入维数与时延，M=N-(m-1)τ表示相点数。

选取合适的嵌入维数m与时延τ，在拓扑等价的意义下按照Takens定理令系统恢复初始动力学形态，系统在m维相空间内的变化轨迹通过相点间的连线表示[8，9]。通过Takens定理确定该相空间嵌入维数的界限值，以其为重构后的样本数，嵌入维数m大于该状态空间奇异吸引子维数(d)的2倍，表示为m>2d。

重构相空间时，其质量直接受选取嵌入维数与时延的影响。选取的嵌入维数太高，相邻点间的距离较远，选取的嵌入维数太低，吸引子产生自交性；选取的时延太大，令原本距离较近的向量被拉远，系统状态难以确定，选取的时延太小，重构吸引子相邻点具有强相关性，导致噪声极易干扰吸引子的分析[10]。

2.2 确定最佳嵌入维数与时延

嵌入维数与时延的关系紧密，不能相互独立计算、选取，确定需要求取的参数值时应该与时间窗τW=(m-1)τ相结合。

选用C-C算法，利用序列的关联积分组成描述非线性时间序列相关性的统计量，利用统计量与时延之间的关系同时获得τ与τW，并对嵌入维数m进行确定[11，12]。定义关联积分为

(3)

(4)

划分时间序列{x(t)|t=1，2，…，N}为t个不相交的子时间序列，针对该子时间序列有：

S(m，N，r，t)=

(5)

取所有S(m，N，r，t)平均值得到

(6)

其中，m表示嵌入维数的数目，J表示r的数目。将有关r的最大偏差定义为

ΔS(m，t)=max{S(m，rj，t)}-min{S(m，rj，t)}

(7)

分别计算下面3个变量

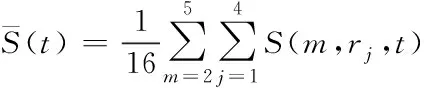
(8)

(9)

(10)

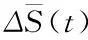
2.3 流量初步预测

不同断面之间存在短时动态交通流时延特性，其主要体现在交通流流量在时间维度上的分布延迟，存在

fa(t)=fb[t+d(t)]

(11)

其中，断面a的流量随时间的变化通过fa描述，断面b的流量随时间的变化通过fb描述，断面a与断面b间的时延随时间变化的函数通过d(t)描述。

对时延特性的相似性度量与流量进行初步预测，总体过程包括：切分并重组输入数据，对目标断面与其它断面短时流量间所隐含的时延特性进行抓取。选取当前时刻与长度均为k的连续子序列，以其为结束时刻和当时该断面的流量特征，对各断面某一时刻的短时流量进行描述。分析输入数据长度与相似性比较可靠性，在其基础上选取子序列长度，较短的子序列时延范围较长，但相似性鲁棒性受其影响会减弱，数据受易噪声干扰。因此，只需考虑目标断面Pi(i是该断面的序号)末尾时刻的流量特性，可得到

Fi，T={fi(t)|t=T-k-1，…，T}

(12)

其中，输入时间序列的末尾时刻通过T表示，目标断面流量随时间变化的函数用fi(t)代表示。

针对通过j描述该断面序号的其它断面Pj，其数据被遍历时延列表切分，得到不同时刻的短时动态流量公式是

[Fi，T-k，Fj，1，…，Fj，T-1]

(13)

描述目标断面末尾时刻与其它断面各时刻短时动态流量间的相似性度量矩阵得到

P∈ω(m-1)×l

(14)

其中，断面总数描述为m，切分每个断面输入所得子序列个数表示为l，矩阵的建立需要综合考虑余弦相似度与幅度相似度。定义任意两个短时动态流量特征a与b之间的相似度为

(15)

(16)

(17)

(18)

通过能量归一化不同断面的最佳匹配，对目标断面将来时刻流量预测于幅度上的合理性进行保证，能量增益的定义为

(19)

V′=α×V

(20)

初步预测目标断面将来时刻得到

fi(T+1)=V′×Q

(21)

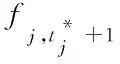
2.4 应用长短时记忆物流预测多断面交通流

建立一个预测值更精确的递归神经网络模型，其以初步预测的目标断面流量结果及原始数据为基础。由于交通流存在时延特性，对数据及学习时的序列时间跨度进行计算时，隐含层的记忆值会受到影响得出较小值，导致梯度消失，所以需要在递归神经网络模型的链式结构中引入长短时记忆单元，增强预测网络的记忆能力。单层长短时记忆网络如图1所示。

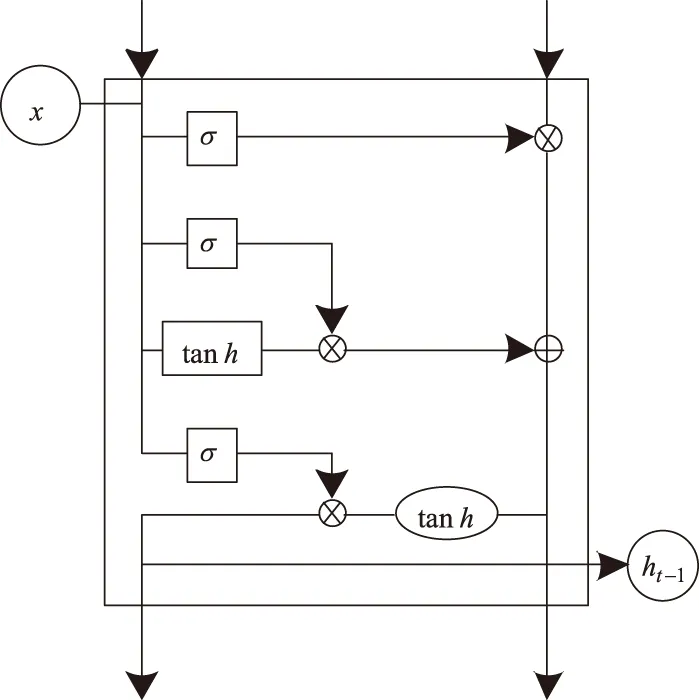
图1 单层长短时记忆网络示意图

图1中，x1、h1分别代表该层输入的t时刻的数据与隐藏信息，σ为sigmoid激活函数，tanh为tanh激活函数。长短时记忆网络的堆叠层数为三，第一层网络输入包括初始数据与初步预测值，其它各层的网络输入都是上一层的隐含层输出。通过初步预测所得标量与原始数据末尾直接串联可得出新数据，去掉完成组合的数据在开始时刻的流量值，保持原始数据和完成重构的数据的相同长度，二者实现共享结构相同的神经网络，然后输出最后一层的长短时记忆单元状态，以其为最终预测值。

3 实验结果与分析

为验证上述基于时延特性的短时动态交通流预测模型的实际应用效果，在MATLAB平台中设计如下实验。

实验对象为某城市干道主方向上连续3个断面的交通流，依据断面编号排列上下游得到其上下游关系，各断面之间的相对距离为1.23-3.21km。采取干道交通流为主要交通流量来源。实验样本是通过相邻20个时刻数据所得出的50000个数据，其中包括40000个训练集样本数、10000个验证集样本数。随机选取连续5天的真实流量数据(仅包括断面流量特征)，将实际输入数据长度与相似度比较的可靠性相结合，子序列长度设置为10bit。

为避免实验结果的单一性，将文献[6]中的基于XGBoost的短时交通流预测模型和文献[7]中的基于分形与三次指数平滑的交通流量预测模型作为对比模型，与本文模型共同对5天内的交通流强度进行预测，并与实际交通流强度展开对比，结果如图2所示。

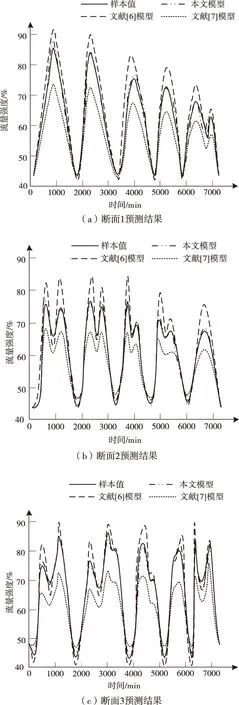
图2 不同预测模型对3个断面的预测结果

通过图2所示可知，3种模型均能有效预测5天内的交通流强度，但文献[6]模型与文献[7]模型的交通流强度预测结果与实际交通流强度之间的差距较大，说明这2种模型虽然能够预测交通流，但其预测结果与实际之间的误差大，效果差。相比之下，本文模型不仅能够有效预测3个断面的交通流强度，并且所预测结果与实际交通流强度高度重合，预测结果与实际之间的误差小，证明本文模型是一个有效且准确的交通流预测模型，能够很好地应用在实际中。

为了进一步验证本文模型的有效性，选取F-measure指标对模型的预测性能进行评价。F-measure指标是一种将预测模型评估指标中的召回率和查准率结合在一起的综合性能指标，可以综合考虑召回率和查询率二者的情况。F-measure综合性能指标的区间为[0，1]，数值越大，代表预测模型的预测性能越好。3种模型的交通流量预测F-measure结果如表1所示。

表1 F-measure对比结果

分析表1可知，本文模型的交通流预测F-measure值大于2种传统模型，表明本文模型的预测效果优于文献[6]模型与文献[7]模型，具备显著交通流预测优越性。

由于实际中的交通流流量较大，因此，深入研究训练集样本数量对本文模型预测性能的影响，结果如图3所示。

图3 训练集数量对本文模型的预测性能的影响

通过图3中可以看出，本文模型的预测平均绝对误差跟随训练集样本数量的增加逐渐减小。当训练集样本数量为15000时，本文模型的预测平均绝对误差降至0.024。随着训练集样本数据继续增加至20000时，本文模型的预测平均绝对误差降至0.016，并在之后的样本数据增加过程中保持不变。实验表明本文模型具有较好的鲁棒性，在训练集样本数据增大至20000时，本文模型可达到最佳预测效果。

4 结语

本研究基于时延特性设计了一种短时动态交通流预测模型，采用交通流时延特性理论，对交通流强度与时延系数间的关系及变化趋势展开研究，在其基础上利用实际交通流流量数据建立相似性度量方法，按照流量匹配的方法对多断面时延系数初步预测的断面流量进行求解，利用三层长短时记忆网络搭建多断面交通流预测模型，从而实现对短时动态交通流的预测。