基于多特征的BP神经网络LSS目标识别方法

卞伟伟，邱旭阳，辛振芳，贾彦翔

(北京机械设备研究所，北京 100854)

1 引言

相比于军事目标，“低慢小”无人机类目标的雷达散射面积小、飞行高度低、速度慢、多普勒频移不明显，加之使用环境的复杂、背景干扰多，使得“低慢小”无人机的探测与识别成为一个世界性难题，多内外都在积极开展“低慢小”目标探测与识别技术研究，研制新型探测装备，以提高对低空/超低空目标的探测、识别和跟踪能力[1，2]。将计算机视觉与图像处理技术相结合的图像识别技术更是得到了长足发展，目前目标图像检测与识别在无人驾驶、机器人、监控监测、图像内容分类与检索、辅助医疗等方面都有积极应用[3]。

利用计算机对图像进行处理加工以达到预期的某种效果，从中提取有价值的信息。目标识别最主要的是特征提取和目标分类。不同的目标分类方法相结合，学者们提出了不同的目标识别方法。文献[4]以均方差与均值之比值来衡量特征的稳定性，并以稳定性排序占优的特征作为不变量特征来结合支持向量机实现飞机机型的快速识别，但没有考虑飞机图像识别环境的复杂性；文献[5]提出了一种WEFT技术将飞机分为机翼、发动机、机身和机尾四个部分的飞机特征提取方法，该方法只经过了理论验证并没有经过实际测试；文献[6]提取飞机目标的7个Hu矩不变量，归一化转动惯量和轮廓离散化参数等特征，并通过概率神经网络识别飞机，该方法使得识别准确率有了很大提升；文献[7]将仿射不变矩、Hu不变矩与傅里叶描述子三个特征相结合，最后使用模糊聚类的方法对飞机目标分类，实现了对二值飞机图像顶视图的有效分类，虽然该方法的识别准确率很高，但是只适用范围较窄，而在大部分的实际应用中，通常不能很好的提取目标的顶视图。

由于圆形度具有旋转、平移、缩放不变性，Hu不变矩具有平移、缩放不变性，仿射不变矩是Hu矩在尺度、平移、扭曲、缩放和旋转等仿射变换后不发生变化的矩特征。因此，本文提出一种基于圆形度、Hu不变矩、仿射不变矩等11个特征的“低慢小”目标识别算法，实现对旋翼无人机、固定翼无人机、城市飞鸟三类“低慢小”目标的检测识别。

2 图像预处理

基于多特征的BP神经网络“低慢小”目标识别方法流程如图1所示。

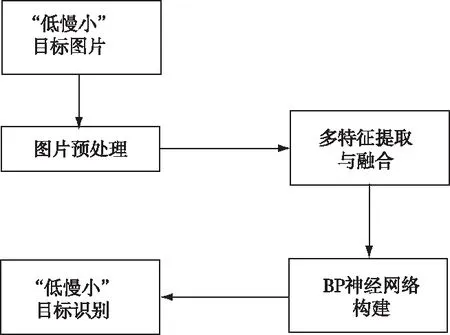
图1 算法流程图

由于特征提取是针对图像中目标进行的，所以，图像的预处理工作对特征提取的好坏起到至关重要的工作；其次，图像中感兴趣区域(ROI)的提取、过滤图像中的噪声、处理目标轮廓的毛刺，都需要进行图像的预处理工作。本文采取的所有图像是利用型号为Mars-5000的黑白图像传感器，采集的图像为8位黑白图像，配合10mm-100mm的10倍变焦镜头，拍摄的“低慢小”目标效果较好。对拍摄的灰度图像采用“canny”算子边缘检测，得到只会存有目标轮廓的二值化图像，然后填充目标轮廓，得到包含目标二值化图像，利用这种方法实现自适应二值化方法。配合形态学操作，其中，开操作能够去除不包含结构元的部分，平滑目标轮廓，去掉细的毛刺；闭操作能够连接窄的断裂并填满细小的“港湾”。使用多次开、闭操作，实现目标轮廓平滑。

本文拍摄到的“低慢小”目标图像经过自适应阈值二值化后得到如图2-图4，分别是旋翼无人机、固定翼无人机和城市飞鸟三类二值化图像。

图2 旋翼无人机二值化图像

图3 固定翼无人机二值化图像

3 特征提取与融合

“低慢小”目标的特征提取是目标识别的前提，更是对识别结果起着至关重要的部分，本文对具有不变特征的几类全局特征进行研究，包括目标圆形度、Hu不变矩和仿射不变矩特征。

3.1 圆形度

目标的圆形度是目标几何特征的一种，是指目标的外轮廓与圆形的相似程度的量。圆形度的定义如式(1)

(1)

式中，As表示目标区域面积，Ls表示周长。圆形度ρc的值不超过1，越接近1时，表明目标形状越接近于圆形。

在式(1)中，目标的周长Ls是指目标外轮廓的长度。计算过程为：在得到目标外轮廓后，计算目标轮廓的长度。由于轮廓线上不仅有水平、垂直还有斜对角方向的移动，因此不能简单的对轮廓线上的像素值进行累加，因此轮廓周长计算公式通常定义为[4]

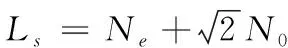
(2)

式(2)中，Ne为边界的方向码为偶数的像素个数，N0为边界上方向码为奇数的像素个数。其中方向码是针对于图像轮廓轨迹而言的，定义如图4所示。

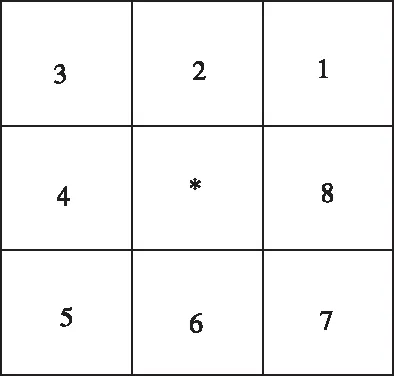
图4 方向码定义

而式(1)中的面积As是指目标连通域中像素点的总数。

目标的圆形度与其它几何特征不同的是，圆形度具有平移、缩放和旋转不变特性，是一种良好的表示目标特征一个全局数据。

3.2 矩

矩作为一种完备的数学表示，其可以用于包含目标物体的区域的特征计算。一个区域的矩特征，是根据感兴趣区域的所有像素点计算而来的，对噪声具有较好的抑制作用。其中，Hu不变矩、仿射不变矩特征都是比较常见的不变矩特征，而且是由普通矩变化而来。

用f(x，y)表示为一幅图像的灰度分布，则这幅图像的(p+q)阶矩定义为

mpq=∬xpyqf(x，y)dxdy

(3)

式中，p，q=0，1，2，3…

图像的(p+q)阶中心矩定义为

mpq=∬(x-x0)p(y-y0)qf(x，y)dxdy

(4)

矩心(x0，y0)为

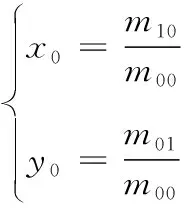
(5)

一般地，对于数字图像，其普通矩和中心矩分别为

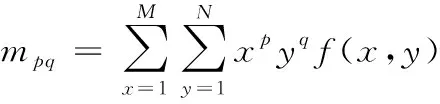
(6)

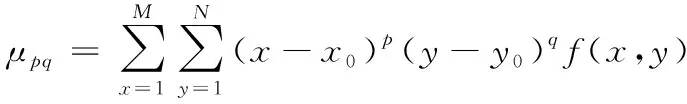
(7)

当图像发生变化时，mpq也发生变化，μpq虽然具有平移不变性，但是不具有旋转不变性，为此，引入归一化中心距，其定义为

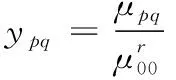
(8)

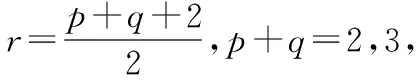
相对比于普通矩和中心距它不仅具有平移不变性还具有比例不变性。

3.2.1Hu不变矩

Hu矩又称为几何矩，它是Hu于1962年首次提出，具有平移旋转，尺度等不变性。Hu矩是利用二阶中心距和三阶中心距构造出的七个不变矩，它们在连续条件下可以保持平移旋转和缩放不变性[5]，定义如下

I1=y20+y02

I3=(y30+3y)2+(3y21-y03)2

I4=(y30+y12)2+(y21+y03)2

I5=(y30-y12)(y30+y12)[(y30+y12)2-

3(y21+y03)]+(3y21-y03)(y30+

y21)2[3(y30+y12)2-(y21+y03)]

I6=(y20-y02)[(y30+y12)2-(y21+

y03)2]+4y11(y30+y12)(y21+y03)

I7=(3y21+y03)(y30+y12)[(y30+y12)2-

3(y21+y03)2]+(y30-y12)(y30+

y12)[3(y30+y12)2-(y21+y03)2]

(9)

3.2.2 仿射不变矩

仿射不变矩是Jan Flusser从代数的角度提出来的，它具有仿射不变性，能识别出姿态变换之后的目标。

假设空间上的一点P的坐标为(x，y)，它经过仿射变换后，在仿射坐标系中的坐标为(x′，y′)，那么对应的仿射变换模型为

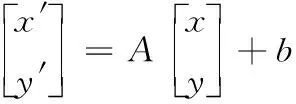
(10)

式中，A是仿射矩阵，表示为

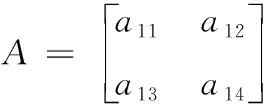
(11)

要满足仿射变换A必须是非奇异矩阵，也即detA=0。当A分别经过尺度变换，伸缩变换和扭曲变换以及旋转变换后，A可以表示为

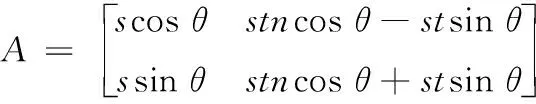
(12)

一般情况下，普通的矩函数包括Hu矩在经过上述尺度、平移、扭曲、缩放、旋转等仿射变换后都会发生改变。然而存在一个仿射矩，在经过上述变换后，不发生改变，它是由中心距构造出来的，一般情况下采用2-4阶中心距来构造仿射不变矩，可表达如下

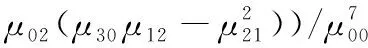
(13)

仿射不变矩具有的仿射不变的特性。由于Hu不变矩特征和仿射不变矩特征的阶次非常高，在提取时，对其进行对数变换和绝对值变换，将其区间变换至[0，10]，防止特征数据差异较大。

3.3 特征融合

针对输入的图像，将上述圆形度、Hu不变矩、仿射不变矩等特征提取以后，可数据融合为：

xij={ρc，I1，I2，I3，I4，I5，I6，I7，F1，F2，F3}

(14)

式中，i表示图像中目标类别，j表示第j张图像获得的数据。

上式可表示为

Fi={fi1，fi2，fi3，fi4，fi5，fi6，fi7，fi8，fi9，fi10，fi11}

(15)

将上述获取的某一特征表示成

fk={f1k，f2k，f3k，f4k，f5k，f6k，f7k，f8k，f9k，f10k，f11k}

(16)

式中，k=1，2，…，N，其中N表示样本数量。

求取上述向量中的最大最小值，并归一化得

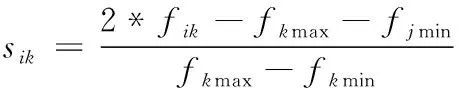
(17)

归一化后数值区间为[-1，1]，该方法消除了特殊值引起的误差[8]。

4 BP神经网络构建

BP(Back Propagation)神经网络是一种信号前向传递、误差反向回馈的有监督的神经网络，具有自学习能力的优势[6]。一个三层的BP网络就可以完成任意的m维到n维的映射。即这三层分别是输入层(I)，隐含层(H)，输出层(O)，如图5所示。

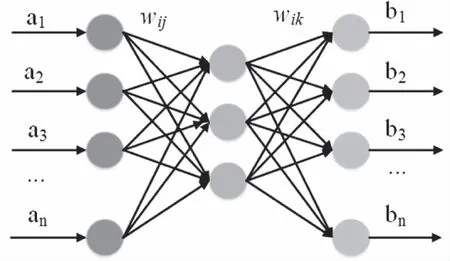
图5 三层BP网络示意图

图中，a1，a2，…，an为输入值，b1，b2，…，bn为输出值，wij为输入层与隐含层间的权值，wik为隐含层与输出层间的权值。

信号从输入层进入，经隐含层逐层处理直到输出层输出，如通过神经网络的输出值和期望值不一样，则会产生一个误差信号，并反馈回神经网络进而对网络的权值和阈值进行调整，调整直到网络输出值与期望值间的误差低于所要求的水平为止。

网络训练过程如下：

1)初始化网络的各权值和中间层阈值(x)、输出层阈值(y)，并根据输入输出的特征数据确定输入层的神经元个数(n)、中间层神经元个数(NN)及输出层神经元个数(m)；

2)确定学习速率和激励函数，通常赋予的学习速率为0.01，然后结合输入数据、wij和x计算中间层输出(t)，并结合t，wik和y，计算出输出值(b)；

3)网络输出值和期望输出值间会产生一个误差信号，误差信号反馈回神经网络，对网络权值和阈值进行调整，并重新计算网络输出值，迭代直到网络的误差达到指定标准，此时的网络输出值基本接近于期望输出值。

5 算例与分析

本文选取三层BP神经网络将上述筛选的11类“低慢小”目标图像特征作为神经网络的输入，因此，该网络输入层的神经元个数为11(n=11)。将“低慢小”目标作为输出层，对旋翼无人机、固定翼无人机和城市空飘热气球三类“低慢小”目标进行分类，若输出值接近于“1”，则可判别该“低慢小”目标为旋翼无人机；若输出值接近于“2”，则判别该“低慢小”目标为固定翼无人机；若输出值接近于“3”，则可判别该“低慢小”目标为城市飞鸟，所以输出层的个数为1(m=1)。

除却输入层和输出层，隐含层的个数为1，隐含层的中间神经元个数由下述经验公式确定[7]

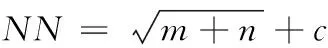
(18)

式中，c为1至10的常数，通过计算可得隐含层的神经元个数NN为5至14。

“tan-Sigmoid”函数，Sigmoid函数又称之为S形函数，是神经网络中常用的非线性函数。三层BP神经网络第二层即隐含层神经元个数为10，输出层的个数为1，则隐含层之间的传递函数(激活函数)为

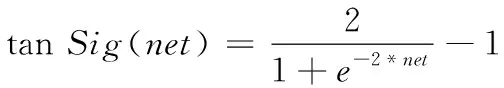
(19)

其中，net为上层神经网络神经元输出，即本层神经网络神经元的输入，该激活函数的作用为通过将输入数值映射到非线性域，使输出更加复杂，解决数据线性不可分问题。

MSE(Mean squared error)损失函数，即均方差函数，它是预测数据和原始数据对应点误差的平方和的均值，可表达为

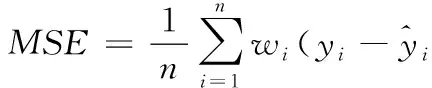
(20)

选取的三类目标图像总共600张图像数据，其中，选取每类150张作为样本训练集，剩下各50张作为样本测试集，训练过程如图6。

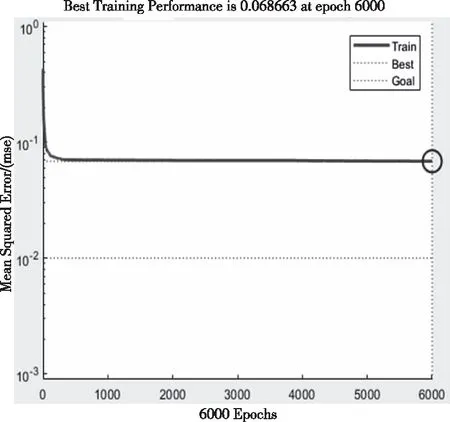
图6 迭代6000次以后的损失函数值

在使用450张三类具有“低慢小”目标轮廓的二值图像训练神经网络后，得到的损失函数值为0.0687，初始损失函数值为0.431，目标损失函数值为0.0100，在经过6000次数据迭代后，损失函数下降了使用450张三类具有“低慢小”目标轮廓的二值图像训练神经网络后，得到的梯度值为0.000561，初始梯度值为0.334，目标梯度值为1×10-7。150张测试集图片得到的测试结果如图8所示。

得到的训练梯度如图所7示。

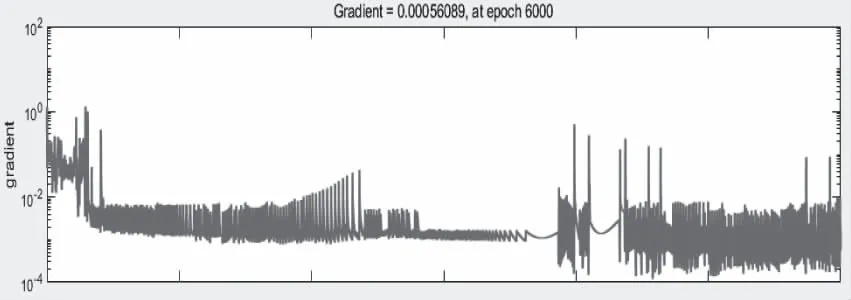
图7 迭代6000次以后的梯度值

根据图8统计，150张测试测试集数据识别错误个数为11，正确率达到92.67%，达到了预测分类的效果。

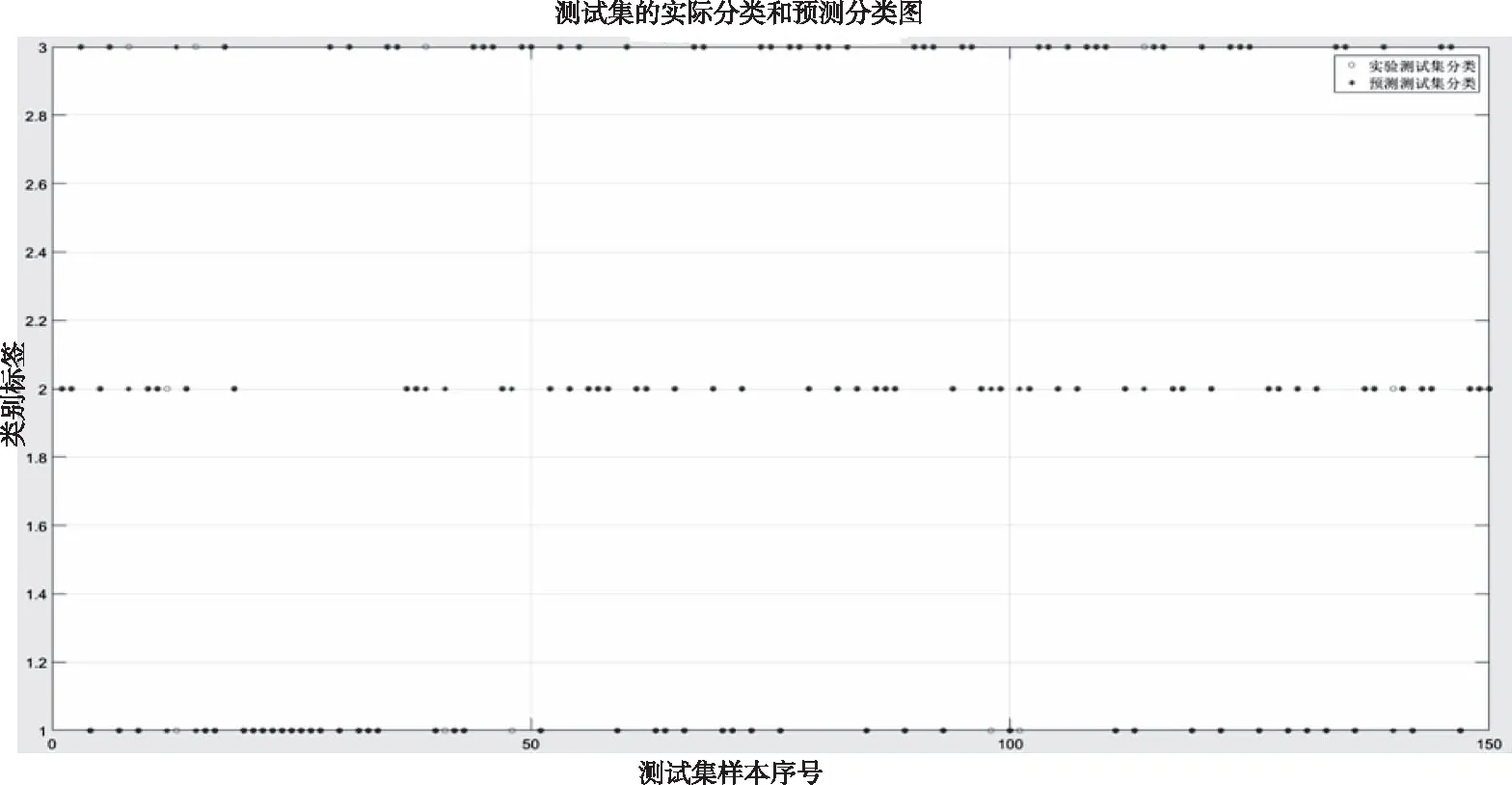
图8 测试集的实际分类和预测分类图

6 结束语

本文通过对“低慢小”目标图像进行预处理，得到三类“低慢小”目标的轮廓二值图像，对其将进行不变特征提取，随后使用BP神经网络对其进行目标识别。实验结果表明，该方法能够有效的实现图像单一目标的识别分类。