基于移动代理的WSN压缩数据采集方法研究*
潘琢金,蒋欣格,王传云,罗 振
(沈阳航空航天大学计算机学院,辽宁 沈阳 110136)
1 引言
无线传感器网络(Wireless Sensors Network,WSN)是一种资源受限的网络,数据聚合是WSN中无线路由的基本模式,它可以组合来自不同源的数据,消除冗余,以最大限度减少传输次数和通信带宽,从而节省能量[1]。压缩感知(Compressive Sensing[2],CS)理论的出现给WSN数据聚合提供了新的可能[3]。
近些年来,许多学者将CS应用在WSN的数据采集中,主要需要考虑的就是WSN的拓扑结构和路由机制:文献[4]基于CS建立数据聚合树来提高网络效率,文献[5]提出了两种将CS应用在WSN网络层的数据聚合机制(Plain-CS和Hybrid-CS),这两种方法都是基于最短路径树(Shortest Paths Tree,SPT)设计,Plain-CS将CS直接应用到WSN的路由中;Hybrid-CS则只在高于传输次数的节点处执行CS,其余节点沿路由逐跳转发数据,实验证明Hybrid-CS具有更高的吞吐量和更低的能耗,但是同样具有网络负载不均衡的问题。文献[6]将压缩数据收集与稀疏随机矩阵结合提出了最小生成树投影(Minimum Spanning Tree Projection,MSTP)算法及其扩展算法eMSTP,稀疏矩阵足够实现数据重构,且大大减少投影次数,随机选择额外的投影节点,再根据投影矩阵中非零元索引的节点向投影节点进行投影,但使用额外节点,会产生大量通信能耗。文献[7-9]提出了一些面向分簇WSN的压缩数据采集方法,在时空上消除簇间冗余,减少簇头数据转发量。文献[10]中提出了基于能耗均衡的稀疏数据采集算法(MA-Greedy),将移动代理(Mobile Agent,MA)应用到对稀疏数据的采集上,为稀疏测量矩阵的每一行分配一个MA,并对MA访问节点的路径进行动态规划。实验证明了该算法在能量均衡上的良好性能,但动态规划决策时延较长,若参与一次投影的节点在地理位置上的分布稀疏分散,单个MA进行采集的行程会较长,通信成本增加,实时性较差。
针对以上问题,本文提出一种基于移动代理的压缩数据采集方法(Mobile Agent Based Compressive Sensing Data Gathering,MACDG),该方法从降低网络传输量、均衡网络负载和减少网络总能耗的角度出发,充分利用测量矩阵中的信息,将测量矩阵拆分分组,每组的采集任务分派给多个移动代理协同执行,分散MA的负载,同时结合混合压缩感知的思想对数据进行压缩采集和重构。
2 模型建立与分析
2.1 网络模型
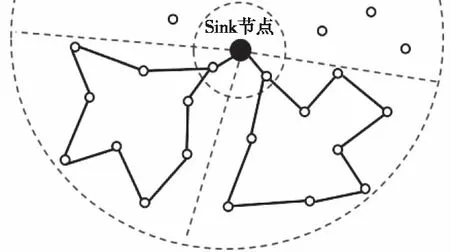
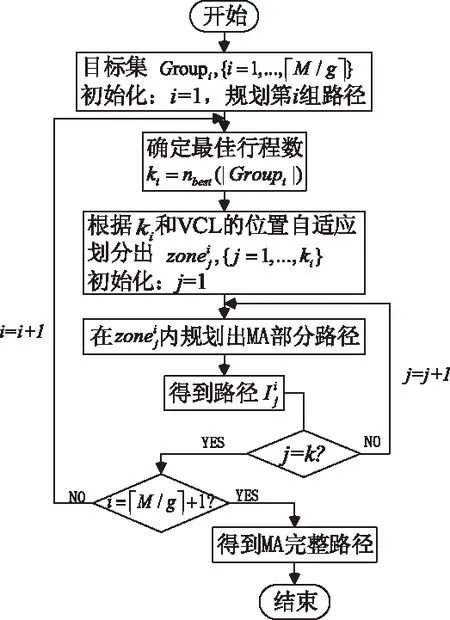
本文用连通图G(V,E)来描述特定监控区域内部署的WSN的拓扑结构,其中网络中的节点集V={SN0,SN1,…,SNN},SN0为Sink节点;若任意两个节点SNi和SNj之间可以互通,则它们之间存在一条通信链路l(i,j),所有通信链路构成的集合E={l(i,j)│1≤i 1)网络中所有的传感器节点均为同构节点,且具有唯一的ID标识;Sink节点的存储能力、计算能力和能量均不受限制; 2)Sink节点位于区域中心,传感器节点均匀随机分布在区域内,一旦部署就不再移动或移动缓慢; 3)所有传感器节点能通过北斗或网络定位等获得空间位置信息; 4)传感器节点的发射功率不是固定的,其值可以根据传输距离在一定范围内适当调整。 压缩感知理论是由David等人于2006年提出的一种稀疏信号或可压缩信号的采集算法,可以通过非线性重建算法完整重建原始信号。将CS理论应用到WSN的数据采集中,就是将一段时间内网络中N个节点的感测数据视为一组离散信号x=[x1,x2,…,xN]T,x在某个稀疏基Ψ下可稀疏分解为 (1) 其中Ψ∈RN×N,s为k稀疏的N×1维列向量,k≪N。x在M×N维测量矩阵Φ下进行随机投影: (2) 其中传感矩阵A=ΦΨ,k Candès等人给出了证明[11],只要传感矩阵A满足约束等距(Restricted Isometry Property,RIP)条件,即对于任何δk∈(0,1),s为k-稀疏信号,并满足δk为(3)式中的最小值 (3) 且测量次数M满足M≥c·k·log(N/k),则可以通过求解式(4)中的l0范数或l1范数最小化问题来重构数据。 (4) s.t.y=As 鉴于移动代理能够自主迁移到节点执行任务,节省了将矩阵信息通知到节点的传输能耗,且不要求节点传输数据具有时间同步性,克服网络拥塞等优点,本文将采用MA执行数据的压缩采集任务。由于MA在迁移过程中数据量会累积,所以MA遍历网络节点的访问路径和访问顺序将会决定整个系统的能量开销和性能,MA最优访问路径是一个NP难问题[13]。在CS框架下,基于移动代理的压缩数据采集问题转化成了移动代理的路径规划问题。 多MA协作采集的过程中可能会产生L条路径I={I1,I2,…,Ii,…,IL},路径中主要产生传输能耗和融合能耗。传输能耗又分为节点发送和接收MA的能耗,融合能耗主要指MA在CS框架下采集数据时执行压缩操作所消耗的能耗。 节点发送和接收kbits数据到距离为da,b的节点的能耗分别由式(5)和(6)计算得到 (5) ERx(k,da,b)=k·Rx (6) 其中,Tx和Rx分别表示节点发送和接收单位bit数据的能耗,εamp表示功放电路能耗系数。MA携带kbits数据从节点a迁移到节点b,该过程中的传输能耗为 Etrans(k,da,b)=ETx(k,da,b)+ERx(k,da,b) (7) ⋮ (8) ⋮ (9) 本文提出的路径规划方法属于静态规划方法,在网络初始化阶段,Sink节点需要预先获取节点位置信息。Sink节点通过广播的方式发送位置请求获得节点信息并计算任意两节点之间的欧式距离。由于节点通信能力有限,任意两节点可能不是一跳通信节点,所以利用dijstra算法计算两节点之间的最短路径,以二维数组prev存储最短通信路径的中间节点,以二维数组cost存储节点能够实现多跳通信的最短距离。数据采集开始,传感器节点周期性地采集数据并存储本地。 为了降低移动代理的负载上限同时不使行程数过多且访问位置过于分散,投影部分将分组进行。如图1所示,将ΦM×N拆分成d个矩阵ΦMi×N(i=1,…,「M/g⎤),其中包括⎣M/g」个g×N的矩阵和一个小于g行的矩阵。如果ΦMi×N的每一列中存在非零元素,将该列索引节点添加到兴趣点集合Groupi中,以Groupi作为目标节点集为其分配多个MA进行采集,此时Groupi中数量较多,再进行自适应分区使得区域内节点分布紧凑,尽可能使路径中的节点可以单跳到达。 图1 基于稀疏二进制矩阵的数据采集模型 在典型的多移动代理路由算法中,如图2所示,每个MA的往返路径都收敛于Sink节点,当MA远离Sink节点迁移时行程逐渐扩张,呈现一个扇形路线。不同于TBID[14]算法以贪婪策略选择行程分组,容易陷入局部最优解导致行程过长,本文算法根据节点密度与节点数量自适应的划分区域,为划分后的区域分配MA,大大减少了时间复杂度。 图2 移动代理路径规划示意图 分区方法为将整个区域以相同的圆心角θ划分出k个zonej,其中θ=2π/k。计算区域中心位置节点VCL[15],即节点分布密度最大的位置,调整第一个区域,使VCL位于第一个区域的中心,其它区域在zone1基础上按圆心角θ继续划分。 使用该方法划分区域后,对每个区域内的节点进行动态路径规划,在节点数为100的WSN场景中,划分不同数量的区域,网络呈现的性能如表1。 表1 不同行程数下网络性能值 数据显示,当划分5个区域,即行程数为5时,网络总能耗和往返时延都达到最小,在高于或低于该数值的时候,网络性能呈逐渐下降的趋势,为了寻找节点数N与最佳行程数nbest之间的关系,设 nbest(N)=a·log(N)+b (10) 其中a,b均为常数,通过不同节点数量下的最优行程数的多次拟合得到关系函数。nbest的值由总能耗和时延两个指标通过归一化并加权求和的最小值来确定,即: nbest(N)=min(αE′ (N)+(1-α)t′ (N)) (11) 这里,根据对时延和能耗的要求程度,α可以设为0.7,求得a和b的值大致为11.3529和-18.2267。 在获得兴趣节点集Groupi后,根据集合中节点的个数,其最佳行程数ki=nbest(|Groupi|)。 图3 MA路径规划流程图 利用文献[14]中的数据结构存储二叉树,算法具体步骤如下: 1)在Sink节点一跳邻居节点中,选择距离Sink最近的节点作为SNmin; 4)遍历当前所有行程代价C(SNx,SNy),且attachSNx=0,寻找当前最小的行程代价minC(SNx,SNy),令(SNx,SNy)=(xmin,ymin); 5)将xmin作为ymin的最右孩子节点附加到ymin所在的树上,attachxmin=1; 6)后序遍历当前树中节点并计算行程代价C(SNx,SNy),且满足attachSNx=0,attachSNy=1 8) 后序遍历行程树,确定节点访问顺序,若访问顺序相邻的两个节点并非一跳通信,通过prev寻找两节点最短路径的中间节点,加入行程; 9)输出当前部分路径Iji。 Sink节点派遣MA根据规划好的路径在每组内进行采集并压缩,在每个分组Groupi中,ki个MA均携带Mi个数据返回到Sink节点,并在Sink处再进行一次求和,得到 (12) 每个分组都会返回Mi个测量值,将它们组合到一起,最后得到完整的观测值 (13) 到此,采集工作已经完成,最后Sink节点通过求解l1范数最小化问题将M维测量值重构回原始感知数据,一轮采集任务结束。 本文算法采用基于OMNeT++平台开发的Castalia仿真工具进行仿真,所有传感器节点均采用CC2420无线模块模型,具体配置见表2。 表2 网络配置参数 所有传感器节点随机分布在监测区域,发送器提供了8个功率等级,发射功率从-25dBm到0dBm分别对应于4.22m到46.22m的传输范围,节点间传输数据使用传输范围内的最低等级功率。 由于每轮待采集的感知数据的稀疏度是未知的,稀疏基在每轮采集中可能会变化[16],所以每轮可以根据估计的稀疏度重新调整稀疏基,本文仅对算法性能进行分析。一共通过三个实验对本文算法进行评估:①设压缩率γ=N/M,仿真分别在γ=10和γ=5两种压缩率下,不同网络规模下的网络通信量;②在节点规模为100时,两种随机分布下的能耗负载均衡度;③在γ=10和γ=5两种压缩率下,不同网络规模下的网络整体能耗。 实验结果如下。 实验一:如图4所示,五种算法随网络节点数的增加,网络传输量呈线性递增,且压缩率越小,网络传输量越高,本文方法在两种压缩率下的网络传输量都是最优的。在SPT路由下采用混合CS能明显降低网络传输量;MA-Greedy算法在两种压缩率下的网络传输量都是最高的,每个节点被访问次数都大于等于d次,受M值影响较大。本文方法受M值影响较小,在γ=5,N=100时,对比其它方法的网络传输量,分别下降了53.38%,46.2%,20.21%和66.19%,在网络通信量上的性能有显著提升。 图4 不同压缩率下的网络传输量 (14) 不同的分布可能对能耗均衡性有影响[17],所以观察两种随机分布下的CV值随M从10变化到40的变化曲线。如图5所示,本文方法在5种算法中,CV值最低,能耗均衡性最好。虽然基于SPT算法的网络总能耗相对较小,但是网络远近端节点能耗负载不均衡,负载较高的节点提前死亡,使很多能量未耗尽的节点变成孤点。MSTP算法和MA-Greedy算法在单次投影中,兴趣点分布较为分散,访问过程中需要大量中间节点进行转发,而本文算法增加了单次投影的节点数量,并自适应的将地理位置相近的兴趣点划分到扇形区域,规划路径后访问每个兴趣点都能在单跳通信中完成,且负载上限被有效限制,使得所有节点的能耗更加均衡,能耗均衡度显著优于其它算法。 图5 不同随机分布下的能耗负载均衡度 实验三:网络整体能耗包括节点采集、处理、接收和发送数据的总能耗,同时也包括中间节点转发MA所消耗的能量。实验结果如图6所示,五种方法的网络能耗随网络规模的变大而增加,两种压缩率下,由于额外的投影节点带来的传输能耗,MSTP的整体能耗都最高。γ=10时,算法之间的能耗差距不是十分显著。但在γ=5时,M值随节点数同比例增加,投影次数随之增加,MA-Greedy算法和MSTP算法受压缩率影响较大,在M值较大时,会带来较高的代价。本文方法通过分组投影有效的降低了M值对投影次数的影响,在γ=5,N=200时,对比MSTP算法和MA-Greedy算法,整体能耗分别下降了25.63%和15.35%。由于使用MA会带来额外的能耗,使得整体能耗仍高于SPT算法,但是相比于SPT提高了网络效率并且能耗更加均衡,证明了本文算法的有效性。 图6 不同压缩率下的网络总能耗 本文研究WSN中基于移动代理的压缩数据采集方法,根据测量矩阵进行分组投影,增加单次投影的兴趣点数量,并利用MA进行分区域采集,有效降低M值对网络性能的影响。同时对区域内MA的访问路径进行有效规划,充分考虑MA在实际迁移中的中间转发节点的能量开销。通过仿真验证了使用文本方法对WSN数据进行压缩采集可以进一步减少网络通信量,同时使网络能耗更均衡。2.2 基于移动代理的压缩数据采集模型





2.3 基于移动代理的能耗模型

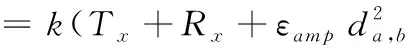





3 MACDG算法
3.1 网络初始化
3.2 分组投影

3.3 自适应分区

3.4 移动代理路径规划



3.5 获取完整测量数据并重构
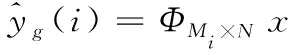

4 实验结果与分析





5 结束语

