云平台安全监控大数据集群调度容错控制仿真

赵 杉

(四川大学锦城学院，四川 成都 611731)

1 引言

集群调度是集群计算的研究热点，其在固定的集群资源条件中，可对数据快速准确地分析处理，得到所需资源，完成预先设定的执行目标。随着集群技术的发展，在大数据背景下其调度场景及目标逐渐复杂，传统集中调度构造的瓶颈被逐渐放大。所以相关学者开始探索新的集群调度构造[1]。

文献[2]提出负载的自适应调度策略，在进行集群执行节点与提交作业性能监控时，根据得到的监控数据进行建模，量化节点的综合计算能力，将节点以及作业的性能信息在调节器上进行融合。在调节中启动评估动态调度方案，识别集群节点的执行能力差异，同时依据作业的任务实时进行细粒度的动态资源调节。因此在对Hadoop YARN资源进行完善调度语义时，可作为子级资源调度的方案构造在上层的调度器中，实现并检测此策略性能。但该方法存在调度数据切换不流畅的问题。

文献[3]提出基于云存储的框架分布式大数据安全容错存储算法。设置数据约束条件时，忽略数据存储节点对中继数据传输链路的影响。将中间链路作为云特性，构建分布式数据的存储容错模型。将数据粒度、数据利用概率以及分布式数据弹性设为已知数据值，同时对数据存储及存储强度计算，把分布式数据存储模型引进数据存储内，实现分布式大数据的云存储。但该方法调度过程干扰因素较多、耗时较长。

为此本文提出一种云平台安全监控大数据集群调度容错控制方法，该方法利用阶梯式构建云平台安全监控框架，加强容错控制方法的扩展性和降低容错率。利用3+1集成法对大数据集群进行计算，确定集群中的不确定非线性切换系统，保证在闭环系统下实现数据切换及容错控制系统的运行流畅，完成集群调度容错控制。实验证明，研究方法能稳定运行，且调度耗时短，数据切换更流畅，具有一定的科学研究意义。

2 云平台安全监控框架结构

在现阶段云平台安全监控系统中，C/S框架结构使用较多。常见的分布式监控框架有两种[4]：一是集中式，将监控代理(Agent)安装至所有监控节点中，以此对各个节点的监控信息进行收集。通过监控服务器将监控代理收集的信息进行汇集处理[5]；二为阶梯式，在阶梯式框架结构中，需监控节点安装至所有节点外，同时还需选定集中节点，安装资源集中代理，而该节点即相当于局部监控服务器[6]。

通过对比两种安全监控框架发现，集中式方法可以统一安装监控代理过程较简单，但可扩展性及容错性较差；而阶梯式监控代理过程较难，但可以将收集的信息和计算任务平均分配至各汇集节点上，对监控服务器负担较小。即使某个集中节点出现错误，也仅限所属区域，其容错性能更好。具体框架示意图如图1所示[7]。

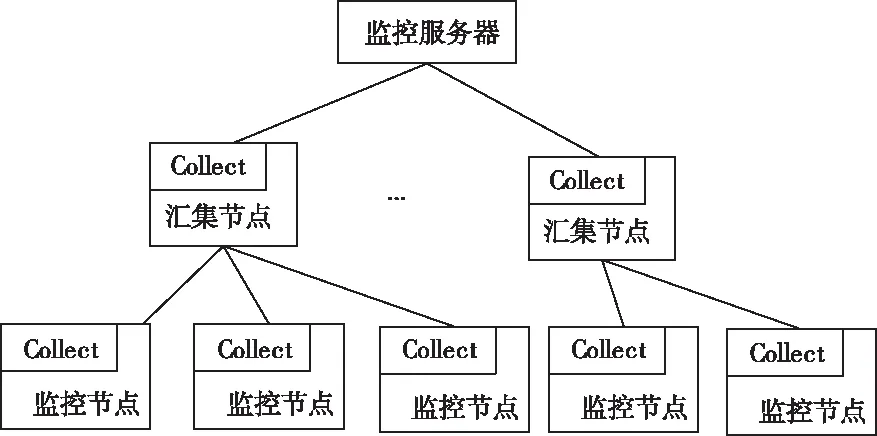
图1 云平台安全监控框架结构

3 大数据集群调度容错控制

3.1 大数据集群调度分析

利用3+1集成算法中的CPU信号强度波动计算方法，对数据要素引进面延伸优化，再拓宽要素的载入通道。同时需要在底层CPU内对数据进行调度分析，检测信号强度。通过数据处理消耗处理器的资源量，其动态调整计算逻辑需采用要素，完成通道量载入，以此削弱CPU处理压力，保证其逻辑运算的平稳性。而在进行设计时，要采用CPU-NT对CPU的信号强度波动计算方法进行辅助运算，可有效增加大数据的处理浮点能力以及满载状态中峰值抑制CPU信号强度波动能力，具体计算公式为

(1)

式中：DB代表CPU-NT专用计算方法；其G代表初始数据流；H代表数据流的增量；D代表数据流所增加的峰值系数；而max则代表计算方法动态优化的峰值系数。具体的CPU-NT专用计算方法如下所示

(2)

式中：CPU-NT专用关系的计算方法；K代表辅助点G代表运算增幅量；S代表数据处理增加量的系数；而I则代表动态优化的系数[8]。

经过以上两级计算方法的优化处理，解决了传统数据调度方法内存在数据计算逻辑引进面不够的问题。设计的3+1集成算法，其CPU的信号强度波动计算方法及辅助CPU-NT的专用计算示意图如下所示：

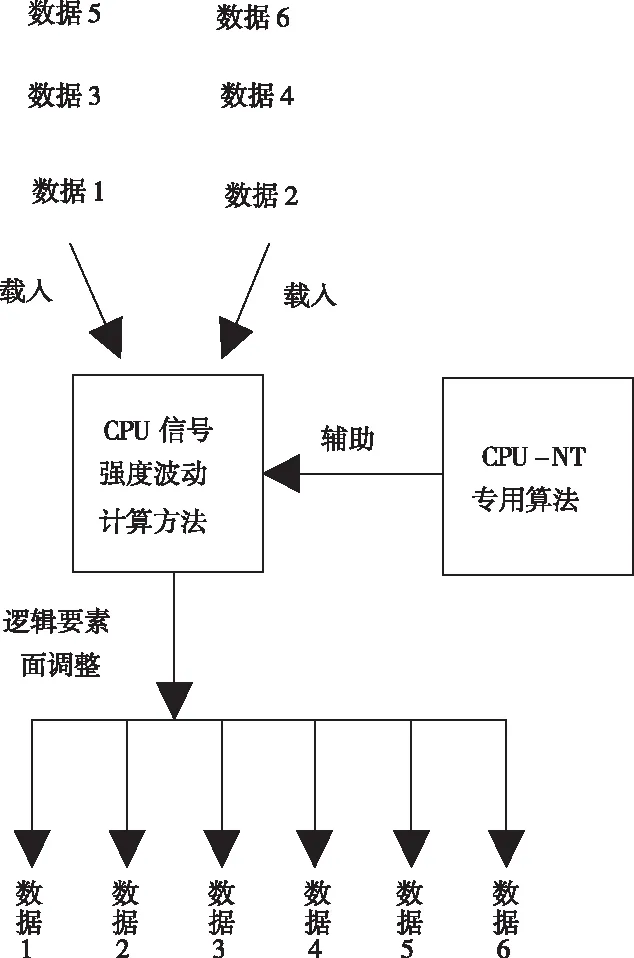
图2 算法工作原理

为确保3+1集成法CPU信号强度的波动计算方法在运行流程中的平稳性，需对大数据的数据节点动态进行优化处理。利用数据处理器的动态数据检测技术，对大数据内部节点进行特征绑定，依据各数据之间的互相交换指数进行判定处理。可对调度数据中噪声点数据进行抗波噪点分析，以达到数据优化的目地。采用大数据动态Flangt计算方法，作为处理器数据节点的动态监测技术，对调度数据整流度进行优化，提升调度信号的响应速度。其大数据动态Flangt计算方法可以与互联网大数据信息资源进行互交，可以确保调度方案的最新度[9]。

3.2 集群调度容错控制实现

确定大数据调度集群的不确定非线性切换系统的稳定性其公式为

i=1，2，…，m

(3)

式中：x∈Rn；u∈Rm；Ai，Bi，Di代表适当维数的已知常规矩阵；ΔAi(t)代表结构扰动的实际值函数；fi(·)：Rn→Rnf代表一个未知的非线性函数；i代表切换信号[10]。

需对非线性系统的稳定性进行证明，具体给出下列引理

引理证明：假如ΔA(t)=MF(t)N，式中的M，N代表适当的维数常规矩阵，并且FT(t)F(t)≤I，即指相对于任意正数ε>0以及正定矩阵的P，其不等式为

ΔATP+PΔA≤ε-1NTN+εPMMTP

(4)

成立。

以下则说明了系统的全局接近稳定性，并且同样也说明了控制器的设计[11]。

定理1：相对于不确认的非线性切换系统，假如相对于说明了一组正数ai，ε1i，ε2i(i=1，2，…，m)以及正定矩阵Q，可以得到矩阵的不等式为

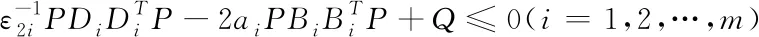
(5)

其正定解矩阵P，即状态反馈控制器公式为

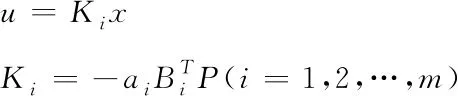
(6)

促使切换系统的闭环系统相对于全部允许的ΔAi，进行任意切换的条件中，其全局接近稳定。

首先需要证明不等式

(7)

(8)

接着建立Lyapunov函数V(x)=xTPx，具体公式为

(9)

通过式(6)以及(7)可以得知

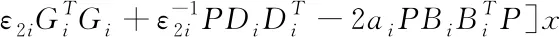
(10)

再采用引理以及式(5)可以得到

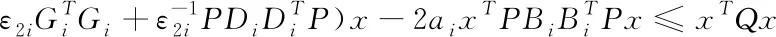
(11)

以此证明结论成立。

现阶段无需对不确认非线性切换系统(3)在执行器失效的情况进行考虑，假设失效的执行器输出数据为0。

定理2：相对于不确认的非线性切换系统(3)，假设一组给定的正数ai，ε1i，ε2i(i=1，2，…，m)以及正定矩阵Q，其矩阵的不等式为：

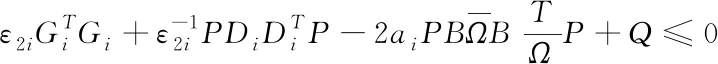
(12)

其正定解矩阵P，即状态反馈控制器(6)能够使系统(3)的闭环信息，对应全部允许的ΔAi以及执行器失效ωi⊆Ωi，因此可以随意切换之后进行全局的接近稳定性。

具体的证明有：因为失效执行器的输出结果为0，因此只有在工作正常的执行器才能使数据起作用，公式为

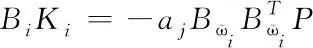
(13)

即可得到

(14)

在经过式(12)以及引理，以此实现集群调度容错控制[12]。

4 仿真与分析

为验证研究方法的有效性，下面设计一次仿真。实验分为三部分，第一部分为数据切换性能的检验。根据不同状态下切换系统对应的响应曲线判断数据切换效果；第二部分为大数据集群调度平稳性能检测。给定相同测验数据，对比研究方法、文献[2]方法及文献[3]方法的实验结果，以此判断研究集群调度效果；第三部分为大数据集群调度耗时检测。对比三种方法运行给定调度时间内，对相同数据的时长，以此验证所提方法的性能。

测试一：基于闭环系统的数据切换效果验证对切换系统进行如下考虑

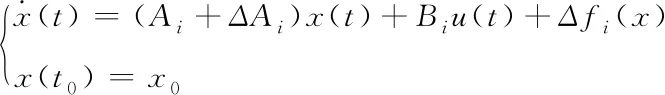
(15)

有两个子系统，其系数矩阵分别为

(16)

(17)

为简化实验系统，所以在传感器失效时进行实验，此系统在原始状态中x0=[2;-1]非常不稳定，因此需采用研究方法得到的接近稳定结果。其结果如图3所示。

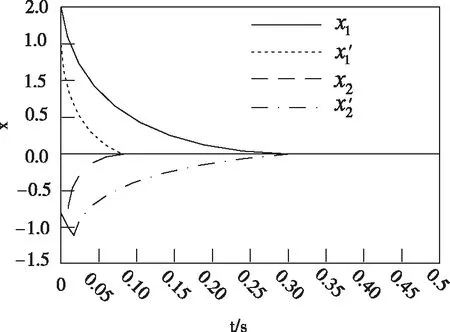
图3 闭环切换系统状态下的响应曲线

其子系统x1、x2在进行切换t=0.5s的作用时，逐渐接近稳定。依据定理2对容错控制的闭环切换系统采用级点配置时，子系统x′1与x′1的极点配置在圆域C(0，9，5)中接近稳定。

而此闭环切换系统的极点配置为圆域C(0，9，5)、C(0，9，15)时，将控制引进u(t)=Kix(t)系统，得到闭环系统的数据相应曲线，结果如图4所示：

图4 闭环切换系统在C(0，9，5)与C(0，9，15)的两种状态中的响应曲线

其极点的配置在圆域C(0，9，15)中，子系统x″1与x″2的收敛速度明显比极点的配置在圆域C(0，9，5)中子系统x′1与x′2的收敛速度快。

通过图4可以看出，其闭环切换系统的影响状态曲线，是在原点处收敛的。可以证明系统存在构造不确定以及带有非线性项是较为稳定的。同时对比图3与图4可以看出，采用研究方法可以使系统的极点配置在响应状态下接近稳定，以此利用选取适当的极点所在区域能够改善系统的动态性能。而利用该系统可以大数据集群调度进行容错控制，其闭环系统运行流畅。证明研究方法的效果较好。

测试二：大数据集群调度平稳性测试

在大数据进行集群调度时，存在较多不安全因素，这些干扰会导致大数据调度不稳定。测试结果如图5所示。

图5 平稳性实验结果

分析实验对比图可知，文献[2]方法在测试期间波动幅值最大，在-10dB～10dB之间；文献[3]方法在测试期间波动幅值较大，在-8dB～8dB之间；研究方法在测试期间波动幅值最小，在-3dB～3dB之间。说明研究方法在大数据集群调度时平稳性极佳。

测试三：大数据集群调度运行时长测试

为验证研究方法的大数据集群调度耗时性能，对比三种方法运行相同数据量的耗时时长。具体实验结果如图6所示。

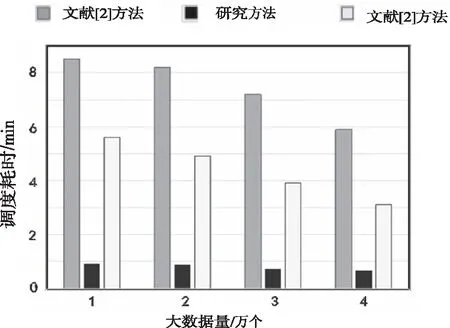
图6 大数据调度耗时实验结果

对比实验结果可知，三种方法的调度耗时均随大数据量递增而减少。文献[2]方法的调度耗时最长，调度不同数据量的时间介于6～8min；文献[3]方法的调度耗时次之，调度不同数据量的时间介于3～6min；研究方法调度耗时最短，调度不同数据量的时间均在1min以下。从而验证了研究方法能高效完成大数据调度，具有实用意义。

5 结束语

1)大数据技术在进行数据调度时，需采用容错控制系统进行问题数据处理。传统方法在进行大数据集群调度容错控制时，流畅性较差，易受干扰因素影响，导致调度耗时长。

2)此次研究提出云平台安全监控大数据集群调度容错控制方法，将监控节点安装至所有节点，选定集中节点安装资源集中代理，构建云平台安全框架。利用3+1集成法中CPU信号强度波动计算方法，对大数据集群进行调度。然后确定大数据调度集群中的不确定非线性切换系统的稳定性，以此完成容错控制的稳定性，实现大数据集群调度容错控制。

3)实验证明，在数据调查出现错误时，研究方法能较好地完成数据间的调度。同时保证其流畅性，且大数据调度过程中波动幅值介于-3dB～3dB之间，说明运行平稳，不容易受其它因素干扰。缩短了调度耗时，调度不同数据量的时间均在1min以下，为大数据集群调度容错控制提供了有利依据。

4)今后将从大数据调度过程的安全性角度出发，进行深入研究，完善大数据集群调度容错控制方法。