基于ABAQUS的通风式制动盘连续制动的热性能仿真研究

赵 崇 王成龙 王睿楠 胡琦琦

(上海汇众汽车制造有限公司,上海 200122)

0 前言

随着汽车工业的迅猛发展及人们生活水平的提高，汽车的安全性和舒适性要求越来越高，制动盘是汽车制动系统的重要构件，其热性能与汽车舒适性和安全性息息相关。汽车制动时会通过制动片与制动盘摩擦生热，将机械能转化为大量热能，而这些热能大部分会被制动盘吸收，制动盘温度急剧升高，进而产生热膨胀，容易引起制动盘的断面跳动，导致制动盘与制动片之间制动力与制动力矩的波动，引起整个制动器的抖动。抖动除了增加制动系统的不稳定性，降低行驶的舒适性之外，还会加快制动盘与制动片的磨损，从而降低汽车行驶的安全性。因此制动盘连续制动的热性能仿真，改善制动盘热性能，降低其热翘曲变形具有重要意义。

本文以某车型通风制动盘为研究对象，基于热分析的理论基础，利用ABAQUS建立了制动盘热-固耦合的有限元模型，得到了十次连续制动温度及热变形结果，并依据对称边界条件，简化了有限元模型，提高了模型的计算效率。

1 热仿真问题与理论描述

制动盘在制动过程中，通过摩擦生热，将车辆行驶中的动能转化为热能散发出去，制动盘与制动片的摩擦生热过程符合库伦摩擦定律。FRIEDRICH[1]研究表明，摩擦过程产生的能量可以近似全部转化为接触面上的热源热量，这样就不需要建立制动片-制动盘制动系统的热-机耦合有限元模型，而是建立只有制动盘的，在接触面加载热源热量的热-固耦合有限元模型；热-机耦合模型结构复杂，需要建立接触非线性边界条件，计算量巨大，精度也不容易保证，而简化的热-固耦合模型简单，热-位移耦合算法成熟，计算量降低，计算精度可以接受。

工程项目中制动盘热分析模型一般有两个基本假设：

(1)制动盘各热力学参数不随温度的升高而改变，包括杨氏模量、泊松比、线胀系数、热导率、比热容等；

(2) 由于制动时间较短，整个过程中热辐射的交换热量很小，故只考虑热传导与热对流两种交换方式。

1.1 热源热量与热流密度

在制动过程中，制动盘的动能除一小部分损耗掉之外，都转化制动盘与制动片的热能，损耗的能量很少，可忽略不计。

dQ=dW=Mωdt

(1)

式中：M是制动力矩，ω是制动盘转速。

其中制动力矩M可表示为：

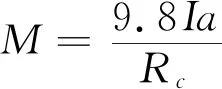
(2)

式中：I为支柱模块中制动盘转动惯量，a为制动减速度，Rc为滚动半径。

假设热流密度在制动区域上是均匀分布的，那么热流密度随时间的变化关系为：

(3)

其中A为有效制动面积。

制动盘动能转化的热能将按照一定比例分配到制动片与制动盘，比例系数与制动盘和制动片的物理参数有关：

(4)

式中：λ1为制动盘热导系数，c1为制动盘比热容，ρ1为制动盘密度；λ2为制动片热导系数，c1为制动片比热容，ρ2为制动片密度。

因此，分配到制动盘的比例系数为：

(5)

制动盘制动区域的热流密度为：

(6)

1.2 热对流

制动盘制动过程同时包括加热与散热两个过程，制动盘散热主要是以热对流的交换方式进行，热交换的热量正比于制动盘与周围空气的温差，即：

q=h(T-T0)

(7)

式中h为对流系数，T为制动盘温度，T0为环境温度。对流系数h与空气的流体参数有关，并且盘面对流系数和通风槽对流系数也有差异，唐旭晟[2]给出了计算对流换热系数的经验公公式，其中制动盘盘面对流系数：

(8)

(9)

式中：ka为空气热导系数，D为制动盘外径，Re为雷诺数。

制动盘通风槽对流系数：

(10)

(11)

式中：dh为流体力学直径，l为通风槽特征长度，Pr为普兰脱数。

其中雷诺数为：

(12)

式中：R为制动盘盘面中心半径，L为制动盘R半径周长，ρa为空气密度，μa为空气动力黏度。

1.3 热传导

热传导是由于物体内部温度梯度引起的热量传递过程，根据傅里叶热传导定律：

(13)

式中：q为某方向传递的热流密度，λ为导热系数，X是坐标系的坐标轴方向。

制动盘温度T是时间域与空间域的函数，即：

T=T(x,y,z,t)

(14)

带入到热导方程中，得到:

(15)

式中k为热扩散率，决定于材料的热传导率、密度与比热容：

(16)

式中：ρ为制动盘密度，c为比热容。

1.4 热边界条件

热传导方程是关于温度的二阶偏导，只能求出通解，若要求出定解，需要施加热传导的边界条件，通常有如下三种边界条件：

(1)第一类边界条件

物体某固定区域上任意时刻的温度已知，例如某些模型以恒温条件作为热源或者某边界上是恒温条件，可以施加该边界。

T=T0

(17)

(2)第二类边界条件

物体某固定区域上任意时刻的热流密度已知，如本文的模型就是施加热流密度作为热源。

(18)

(3)第三类边界条件

物体某固定区域与周围介质进行对流换热，并且对流换热系数已知，制动盘与周围空气进行对流换热，需用到该边界条件。

q=h(T-T0)

(19)

其中，h即为式(8)～式(11)求得的盘面与通风槽对流换热系数。

1.5 连续制动过程描述

本文以连续制动CAE规范与台架规范为依据[3-5]，建立制动盘连续制动热分析有限元模型，其中每次制动都包括三个过程：制动阶段、加速阶段与巡航阶段；制动阶段的初速度为100 km/h，制动强度为0.5g，加速阶段的恢复强度为0.2g，巡航阶段速度同样为100 km/h，单次循环行驶距离为650 m，依次循环十次。

2 连续制动有限元模型

2.1 热-固耦合有限元模型

以某车型通风式制动盘为例，制动盘包括盘面、盘帽、鹅颈和通风筋等几部分。模型采用ABAQUS中修正的热-位移耦合二阶四面体单元C3D10MT，单元尺寸为4 mm。去除模型小倒角与圆角，设置热流密度和换热系数接触面。先根据盘面制动区域设置热流密度接触面，再分别设置盘面换热接触面和通风槽换热接触面，为模板中加载热流密度和对流边界条件做准备。模型材料为HT250铸铁材料，材料参数如表1中所示。

图1 连续制动单次循环示意图Fig.1 Single circle schematic diagram of continuous braking

图2 通风式制动盘Fig.2 Ventilated brake disc

表1 制动盘材料物理参数Tab.1 The material physical parameters of brake disc

2.2 参数计算

模型需要输入热流密度与热对流换热系数，只有制动阶段才有热流的产生，因此减速阶段和巡航阶段不需要热流的参数，并且每次循环制动的转速与时间的规律相同，故十次制动阶段的热流密度也相同，根据式(6)和表2参数可以计算得到热流密度随时间的变化曲线。

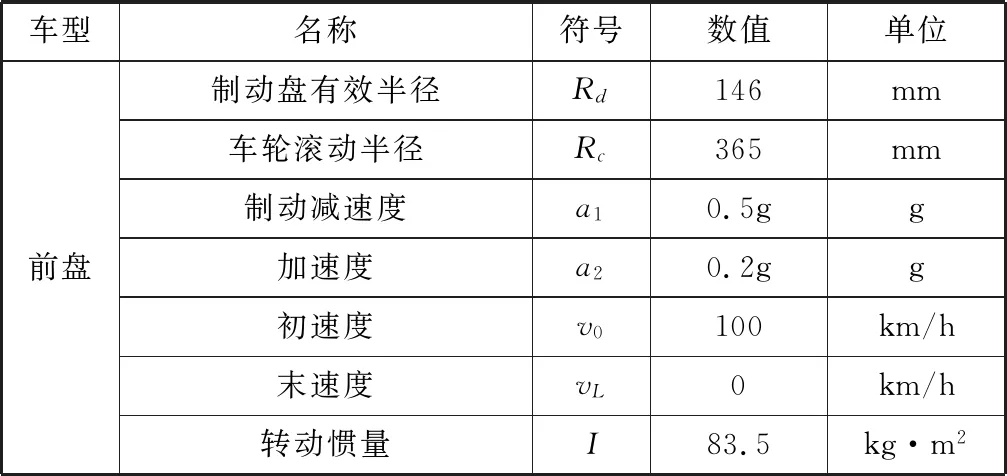
表2 制动盘连续制动工况各参数Tab.2 The brake disc parameters in continuous braking load case

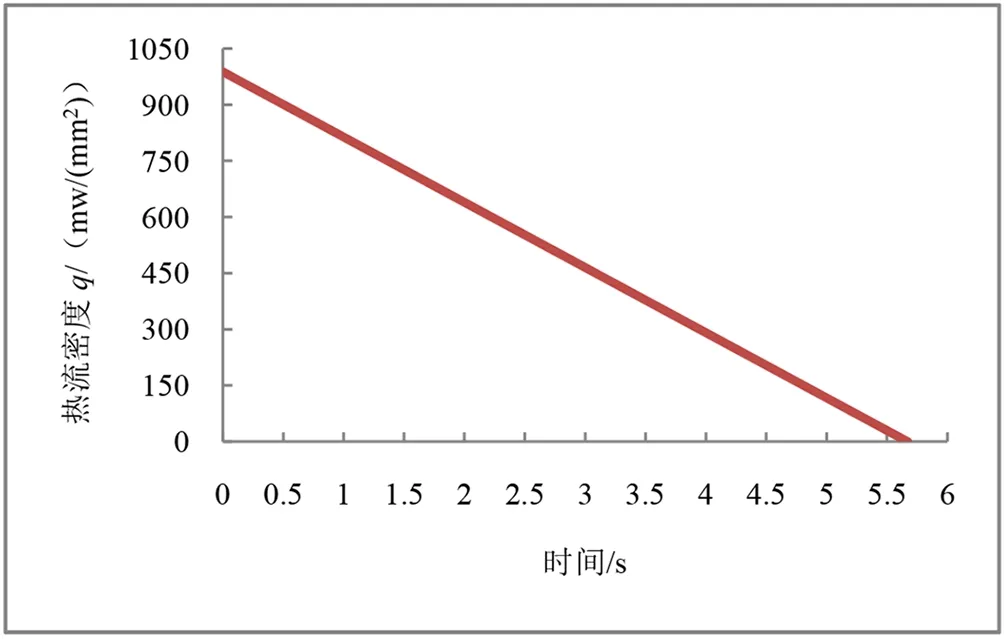
图3 热流密度曲线Fig.3 Heat flux curve

因制动、减速、巡航三个阶段都有对流散热，每个阶段盘面换热系数和通风槽换热系数也不同，因此单次制动共有六个对流换热系数；由于前面假设制动盘物理参数不随温度而变化，所以连续制动每次循环的换热系数不变。根据式(8)～式(11)可以计算出不同阶段的换热系数。

图4～图6分别是制动阶段、加速阶段和巡航阶段的热对流交换系数，盘面的散热性能要好于通风槽，散热系数和制动盘转速成正相关，减速阶段换热系数逐渐减少，加速阶段逐渐增加，巡航阶段不变。

图4 制动阶段盘面与通风槽换热系数Fig.4 Heat transfer coefficient of disk and ventilation slot in braking stage

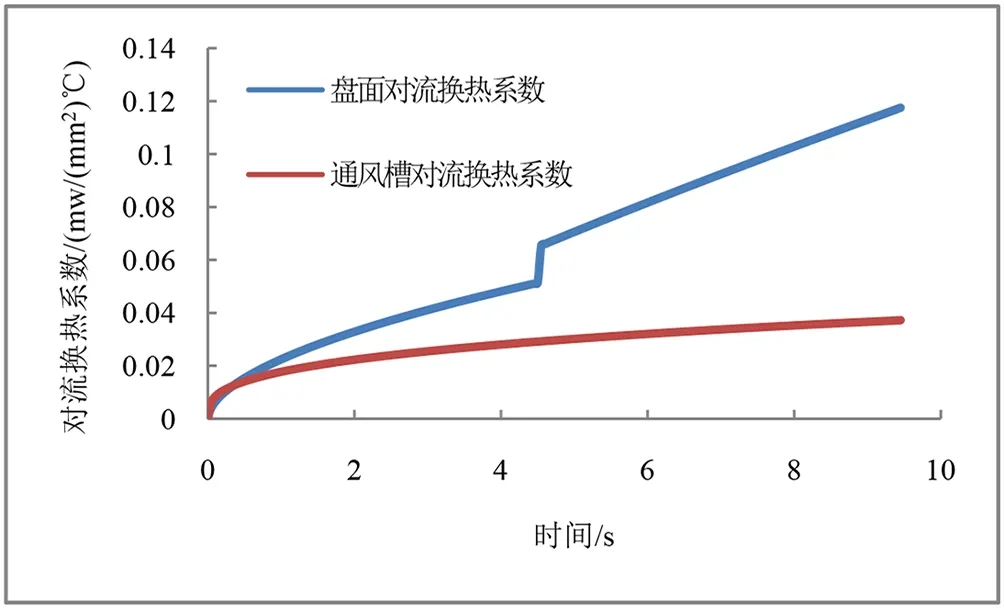
图5 加速阶段盘面与通风槽换热系数Fig.5 Heat transfer coefficient of disk and ventilation slot in acceleration stage

图6 巡航阶段盘面与通风槽换热系数Fig.6 Heat transfer coefficient of disk and ventilation slot in cruise stage

2.3 模型载荷步设置

连续制动每次循环都要制动、加速和巡航三个载荷步，每个载荷步包括加载、边界条件和输出等三部分：

(1)模型加载：将2.1得到的热流密度以幅值的形式加载到盘面的制动区域。

(2)边界条件：包括位移边界条件和热边界条件，位移边界为固定约束制动盘盘帽与轮毂法兰装配接触面；热边界条件将2.1得到的热对流系数分别加到盘面散热与通风槽散热区域，设置环境温度为20 ℃，制动盘初始温度为100 ℃。

(3)输出内容：输出包括节点输出和单元输出，输出节点的温度、位移和单元的应力。

上面为单个循环载荷步，类似的依次施加十次制动载荷步，模型设置完成后，提交分析。

3 计算结果与讨论

用ABAQUS软件计算出制动盘连续十次制动的热分析结果，制动盘在第十次制动结束时温度分布如图所示：

从图7可以看出:

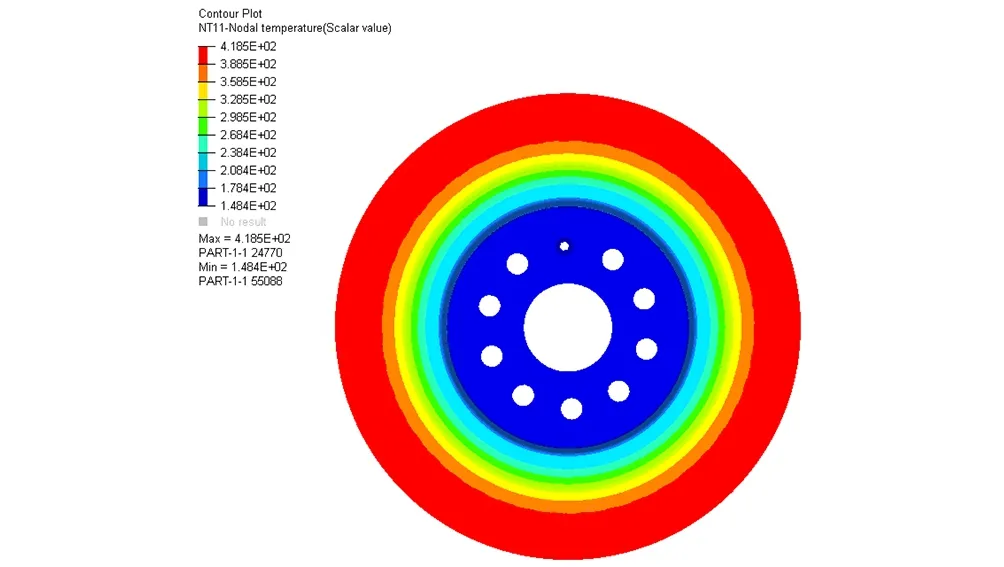
图7 制动盘十次制动温度云图Fig.7 The thermal contour plot of disc ten braking loadcase

(1)制动盘高温区域为制动盘与摩擦片接触区域，其他区域由于没有加热流密度温度较低，制动盘温度环向梯度变化较小，径向温度梯度变化较大。

(2)图8是制动盘盘面中间节点在不同载荷步下温度变化曲线，曲线成“锯齿”上升形状，原因在于制动盘在制动阶段施加热流密度，温度迅速上升，在加速和巡航阶段由于对流换热，温度逐渐降低；另外，随着制动次数的增加，温度上升的速率逐渐下降，是因为制动盘温度升高后，与周围温差增大，散热更加剧烈。

图8 盘面中间节点温度变化曲线Fig.8 The temperature variation curve of disk middle node

(3)制动盘因受热膨胀而产生热变形，如果盘面热翘曲变形过大，制动时会产生抖动现象，因而热翘曲是制动盘热分析的重要参数，其计算方法为盘面外侧垂直于盘面位移减去内侧位移；图9是制动盘热翘曲变形云图，制动盘在十次制动时翘曲为0.238 mm。

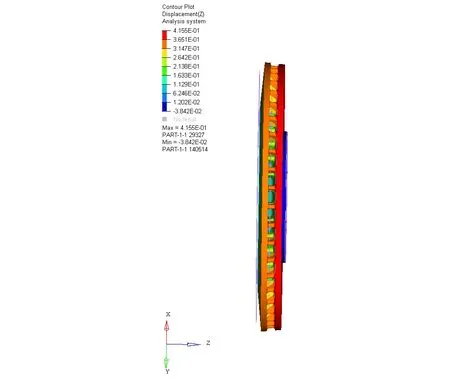
图9 制动盘翘曲变形Fig.9 Brake disc warping deformation

4 有限元模型简化

模型采用的是二阶四面体单元，导致占用内存较大，并且有三十个载荷步，计算时间很长，因此需要对模型进行简化。通风式制动盘各通风筋形状完全相同，其传热和散热方式相同，可以考虑只取四个通风筋部分模型，如图10所示。

图10 制动盘简化模型Fig.10 Simplified model of brake disc

简化模型与整盘模型所加热流密度与对流换热系数等边界条件完全相同，需要考虑的是切口处的位移边界条件和热对流边界条件，由于切口处是镜面对称，可以施加镜面对称边界条件：

(1)热对流边界：切口处不进行热对流和热传导，施加绝热边界条件；

(2)位移边界：在切口处建立局部坐标系，加镜面对称边界条件。

模型其他设置和整盘模型完全相同，计算时间缩短为几个多小时，大大提高了效率。

从图11可以看出，简化模型和整盘模型在第十次制动阶段的最高温度相差6.7 ℃，满足仿真的精度要求；图12是制动盘中间节点温度随载荷步的变化曲线，最大相差6.7 ℃，也满足精度要求。

图11 制动盘简化模型温度云图Fig.11 The thermal contour plot of brake disc simplified model

图12 整体模型与简化模型温度对比曲线Fig.12 Temperature comparison curve between global model and simplified model

5 结论

本文基于ABAQUS软件，建立了制动盘连续制动热仿真分析模型，介绍了制动盘摩擦生热和散热的基本理论，得到了用于模型热边界条件的热流密度和对流换热系数，建立了制动盘热-固耦合模型，为节省计算时间，简化了分析模型，最后得到如下结论：

(1)制动盘连续十次制动最高温升为318.6 ℃，制动盘在十次制动时最大翘曲为0.238 mm，满足设计要求；

(2)制动盘温度曲线成“锯齿”上升形状，在制动阶段温度急剧上升，在加速和巡航阶段由于散热温度降低，并且温度上升的速率逐渐降低；

(3)简化模型与整盘模型最高温度相差6.7℃，满足精度要求。