电磁场效应下HR神经元的全局分岔与参数辨识*

肖冉 安新磊 祁慧敏

（兰州交通大学数理学院，兰州 730070）

引言

神经元是神经系统中最基本的结构和功能单位，通过复杂的放电活动，承担着接受刺激、传递信息等重要职责，且神经元的放电活动具有复杂的非线性动力学特征[1]，因而研究神经元放电活动的动力学行为有着十分重要的意义.上个世纪50年代，Hodgkin和Huxley通过对乌贼轴突触的电压钳位实验数据进行分析，建立了HH神经元模型[2].这是历史上首个神经元放电活动的数学模型.上个世纪80年代，Hindmarsh和Rose通过对丘脑神经元进行研究，建立了HR神经元模型[3，4].近些年来，大量的实验与研究表明，电磁辐射会对神经元放电活动产生影响，且这一影响不可忽略.文献[5]通过非线性动力学理论，分析了HH神经元模型单个及耦合神经元受电磁辐射影响下的放电行为.文献[6]利用非线性动力学理论及数值仿真方法，分析了磁通e-HR神经元模型的动力学特性，并施加Washout滤波器实现了对磁通e-HR神经元模型的隐藏放电控制.文献[7]通过引用磁通变量描述电磁感应下的改进四变量神经元模型，研究了相位同步逼近问题，并发现神经元间的磁通耦合可以产生完美的相位同步.文献[8]研究了电磁刺激对单个神经元以及神经网络系统动力学行为有着显著的调控能力.文献[9]利用磁通变量描述电磁感应的影响，并利用忆阻器耦合实现了磁通对膜电位的调制.更进一步地，通过对神经元施加加性相位噪声，检测了神经元在模态中的动态响应和相变，并观察到双相干共振行为.此外，各个离子通道也会对神经元膜电压产生影响，即通过改变细胞膜内外各离子的浓度，进而改变膜电压大小.文献[10]认为外电场对细胞膜内外各离子通道的传递有影响，从而改变膜电压，并通过引入电场变量，建立了外电场作用下的FHN神经元模型，进一步分析了该模型放电活动动力学特征.但是，上述文献中建立的神经元模型未能同时考虑电场和磁场对神经元模型的影响，有必要在考虑电磁场的情况下再进一步研究.

研究表明，在很多神经元模型的放电活动中也会出现混沌现象，因此研究神经元模型里的混沌控制与同步是十分有必要的.文献[11]利用滑模控制和Mittag-Leffler函数方法，使分数阶惯性神经元主从系统达到混沌同步.文献[12]通过磁控忆阻器建立了一个e-HR神经元模型，并通过自适应同步控制方法，实现了系统混沌态放电到周期簇放电态的同步控制.文献[13]通过建立全局耦合的抑制性和兴奋性神经元网络，发现耦合强度足够大时能够诱导抑制性和兴奋性神经网络达到几乎完全同步的状态.在一般的混沌控制与同步里，参数都是已知的.但实际混沌系统的参数往往难以确定，如混沌系统的参数本身部分未知或全部未知，工作过程中系统参数受到扰动，神经元系统可能会因为外界刺激电流的改变，使得多个系统参数同时发生变化.因此，参数辨识问题是神经元动力学分析中的重要一环.基于Lyapunov稳定性原理的自适应同步方法是目前参数辨识常用的方法[14，15].文献[16]通过增加控制器个数以及取恰当大小的增益系数，保证了HR神经元模型中一组差异过大的未知参数的准确识别，并缩短了识别的暂态过程.

受上述研究启发，本文考虑到磁场以及外电场两方面都对神经元产生影响，同时引入磁通变量和电场变量，构建了一个改进的五维HR神经元系统.运用Matlab软件做出该系统的双参数分岔图，可以看到该系统具有丰富的放电行为及分岔现象，然后对双参数分岔图里的一条黑线做峰峰间期（ISI）分岔图以及最大Lyapunov指数图，发现该系统具有倍周期分岔、逆倍周期分岔、加周期分岔等分岔模式以及呈“锯齿状”的混沌结构.考虑到放电过程中系统可能多个参数同时发生变化，取定一组参数，使系统为混沌态，以其中五个参数为未知参数，利用Lyapunov稳定性原理和自适应同步方法，选择合适的控制器，使驱动系统和响应系统达成同步，同时辨识出未知参数的值.

1 模型描述

基于三维Hindmarsh-Rose（HR）神经元模型，文献[17]考虑到电磁辐射对膜电位的影响，通过加入磁通变量来模拟这一影响，改进成一个四维的Hindmarsh-Rose（HR）神经元模型，再对该四维系统做双参数分岔分析，并通过Washout控制器来实现亚临界Hopf分岔稳定性控制，从而消除了隐藏放电现象.Ma J等[9]考虑到外电场参与细胞内各离子的传递，引起膜电压的变化，引入了电场变量.受上述启发，本文同时引入磁通变量和电场变量，建立磁场电场共同作用下的五维HR神经元动力系统，系统的微分方程如下所示：

其中，五个状态变量分别表示膜电位、快电流、自适应慢电流、模拟细胞周围磁场的磁通变量以及外电场，I为外界的刺激电流，a，b，c，d，r，s，χ0是重要的动力学参数，Ie是磁场产生的电磁感应电流，表达式为-k0(α+3βφ2)x，α和β是与系统相关的确定参数，k2，k3也是确定系数，为磁通反馈增益.因为快电流y对外电场的变化非常敏感，所以对变量y施加一项k1E来表示外电场对变量y的影响.在本文中，各参数参考值取为：a=1.0，b=3.0，c=1.0，d=5.0，s=4.0，r=0.006，χ0=-1.61，α=0.2，β=0.03，I=3，k0=0.1k1=0.1，k2=0.3，k3=0.5，k4=0.2，k5=0.3.

2 双参数分岔分析

神经元模型往往会受到外界刺激，从而使神经元的放电行为发生变化.系统（1）中膜电压x的放电行为与系统参数取值有关，其余各参数取参考值时，系统膜电压x随外界刺激电流I变化的峰峰间期（ISI）分岔图如图1所示.从图中我们可以看到：当外界刺激电流I逐渐增大时，系统（1）首先由静息态进入周期1尖峰放电态，随后经过加周期分岔进入周期2，3，4，5...10簇放电态，再通过倍周期分岔进入混沌态放电，混沌态放电结束后进入周期11的周期簇放电态，再次通过倍周期分岔进入混沌态放电，最后通过逆倍周期分岔进入周期1尖峰放电态.但在实际情况中，外界刺激电流I改变时，系统（1）的其他几个参数可能也同时发生改变.因此研究系统（1）的双参数同时改变时，膜电压x的变化更具有实际意义.

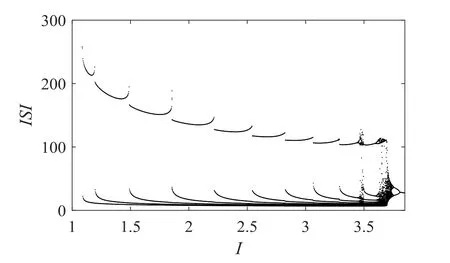
图1 关于参数I的ISI分岔图Fig.1 The bifurcation diagram of ISI with respect to parameter I

取I和r这两个参数，对系统（1）做双参数分岔分析，其余参数取参考值.系统（1）的双参数分岔结构图如图2所示.图中不同颜色对应着不同的神经元膜电压放电状态，右边颜色栏的数值表示对应的周期簇放电状态.（如数字1表示周期1尖峰放电态，数字2表示周期2簇放电态，数字8表示周期8簇放电态，白色区域代表周期大于或等于20的周期簇放电状态或混沌态）.

图2 参数I和r的双参数分岔图Fig.2 The bifurcation diagram with two parameters I and r

对图2做分析可知，当参数I∈ [2.85，3.85]，r∈ [0.002，0.027]时，系统（1）表现出非常丰富的周期簇放电状态和“锯齿状”混沌状态.沿图2中的黑线左上到右下方向，可以看到膜电压x经历的放电过程是：先从混沌放电态进入到周期3簇放电，再由倍周期分岔进入周期6，12，24...簇放电直到混沌放电态，混沌放电态结束后出现周期4窗口，同样经过倍周期分岔进入周期8，16，32...直到进入混沌放电态.一直反复下去.看到系统（1）每经历一次混沌放电，放电的周期数比混沌放电前的周期数大一，这个过程就是伴有混沌的加周期分岔模式.由此可以观察到，随着黑线的走势，周期数不断加大，相应的周期颜色带面积不断减小，且混沌的窗口也不断减小.此外，从I∈[2.85，3.05]，r∈[0.002，0.007]这个参数区间可以看到，此时系统（1）的分岔结构不包含混沌区域的周期层，且相邻周期窗口周期数大一，这个过程称为无混沌的加周期分岔模式.

当以参数r为变量时，其余参数取参考值.沿图2中的黑线从右下到左上方向，可以做出系统（1）膜电压x的峰峰间期（ISI）分岔图如图3（a）所示，图3（b）是图3（a）所对应的最大Lyapunov指数图.从图3（a）可以更直观地看出，随着参数r的不断减小，系统的膜电压x放电模式从混沌态放电结束后进入周期3簇放电态，再通过倍周期分岔再次通向混沌态放电，然后进入周期4簇放电态，进一步通过倍周期分岔转向混沌后再进入周期5簇放电态，以此反复下去，最后从高周期簇放电态通过倍周期分岔进入混沌后，通过一次逆倍周期分岔进入周期1尖峰放电态.

图3 系统（1）的ISI分岔图及最大Lyapunov指数图Fig.3 The bifurcation diagram of ISI and maximum Lyapunov exponent diagram of system（1）

根据上述分析，外界刺激可以导致神经元的放电活动发生变化，系统动力学参数可能也会随之改变.这样在多个系统参数发生变化时，如何辨识出变化后的未知参数就有着十分重要的意义.

3 改进五维HR神经元系统的自适应同步及参数辨识

4 数值仿真

在具体的数值仿真中，令驱动系统中状态变量初值取 (-0.1，-0.2，-0.3，-0.4，-0.5)，响应系统状态变量初值取(0.1，0.2，0.3，0.4，0.5)，未知参数取为a1=1，b1=3，c1=1，d1=5，r1=0.027，此时驱动系统为混沌态，将响应系统初始参数取为a2=1.2，b2=4，c2=1.5，d=6.2，r=0.003.通 过 Matlab软件进行数值模拟，得到响应系统（3）的参数辨识曲线以及同步误差e随时间t的变化如图4所示.可以观察到，经过一定的暂态过程后，同步误差随时间逐渐趋于零附近.驱动系统与响应系统达成同步.且由数值仿真可以得出，在t=1000时，响应系统的参数估计值a2=c2=0.999，b2=3，d2=4.999，r2=0.027，基本趋近于驱动系统的未知参数值，即辨识出驱动系统的未知参数.

图4 系统（3）的参数辨识曲线Fig.4 Parameter identification curve of system（3）

可以看到，基于Lyapunov稳定性理论和自适应同步方法辨识出了五维HR神经元系统的未知参数值，且从仿真结果可以看到同步误差很快趋近于零，辨识结果也较为准确，说明基于Lyapunov稳定性理论和自适应同步方法的参数辨识是成功的.

5 结论

本文首先基于三维HR神经元模型，通过引入磁通变量和电场变量，构建了一个改进的五维神经元系统（1）；其次，利用Matlab软件进行双参数分岔分析，进一步发现其具有丰富且复杂的分岔模式.如沿着图2黑线从左上到右下方向，系统有着常见的倍周期分岔、加周期分岔的分岔模式，混沌结构呈“锯齿状”；然后，取一种混沌状态的情况单独分析，基于Lyapunov稳定性理论和自适应同步方法，以该混沌神经元系统作为驱动系统，构建一个对应的响应系统，设计了使两个系统同步的控制器，使驱动系统和响应系统达成完全同步，从而混沌系统的未知参数得到了识别，理论证明了控制器的可行性；最后，通过数值仿真得到了五个状态变量的误差图以及参数辨识曲线.从图中可以看到两系统较快地达到完全同步，且未知参数得到识别.本文的研究结果在生物学与医学电磁场下神经元模型的建立中有着一定的参考价值.

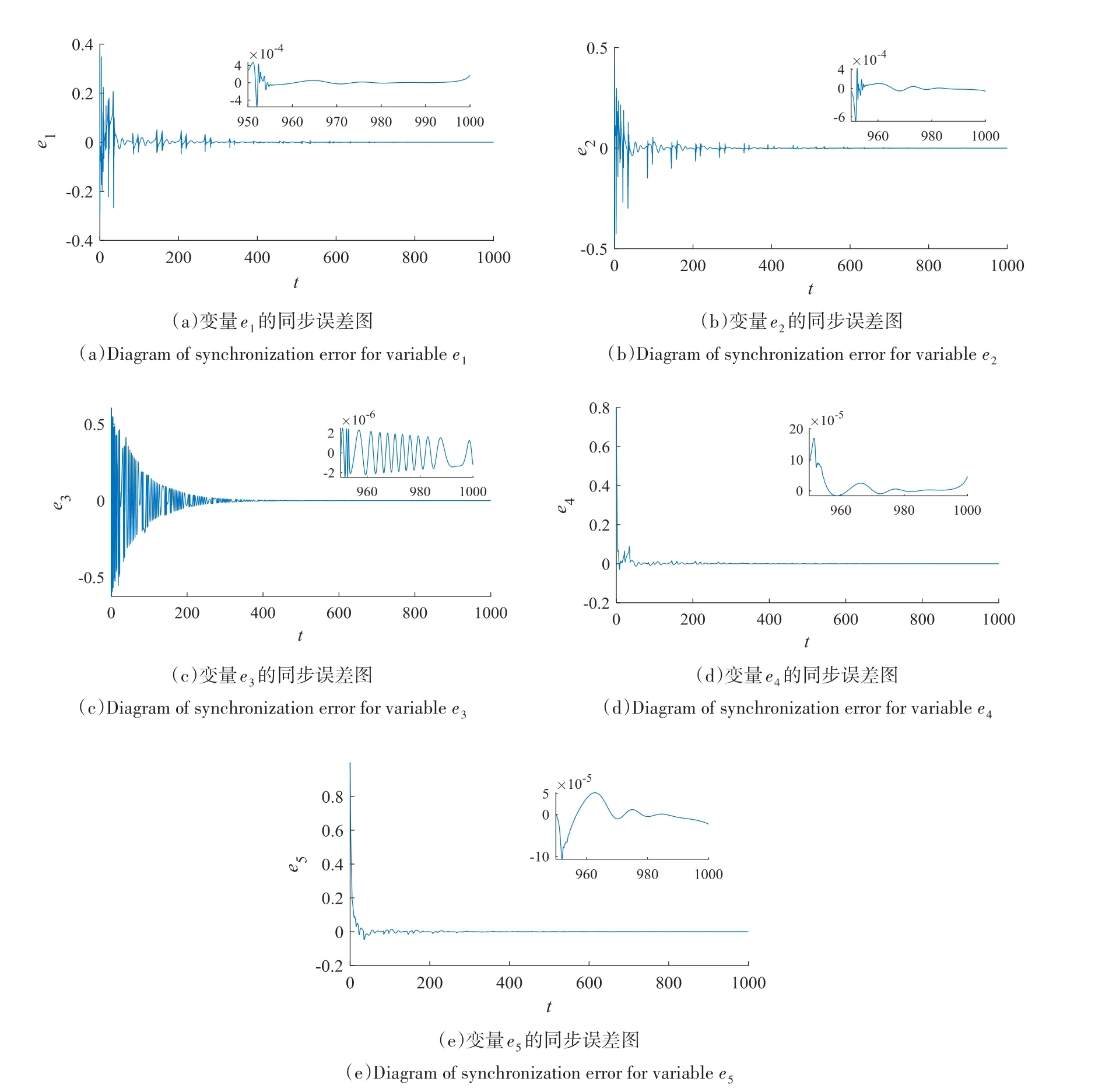
图5 系统（2）与系统（3）同步误差图Fig.5 Synchronization error diagram of system（2）and system（3）