斜交桥墩布设防撞装置影响通航研究

余 葵，孟繁超，刘宪庆，吴威力，毛德涵

(1.重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074；2.重庆交通大学 重庆市桥梁通航安全与防撞工程技术研究中心，重庆 400074)

为响应《全国安全生产专项整治三年行动计划》工作部署，交通运输部在2020年底发布的《船舶碰撞桥梁隐患治理三年行动实施方案》中指出，要求对已建成桥梁进行防撞保护，新建桥梁进行防撞设计[1]。山区通航河段早期建设桥梁受地质、施工条件等原因影响，其涉水桥墩普遍与水流斜交，表1列举了斜交角较大的国内部分斜交桥梁。布设防撞装置是解决此类桥梁通航安全的主要方式之一，斜交桥墩导致涉水桥墩阻水特性增大，安装防船撞装置后使得阻水特性再次增大，船桥碰撞风险增大，因此斜交桥梁通航河段的通航安全问题受到密切关注。

表1 国内斜交桥梁统计表

现有关于船舶通航安全的研究主要有模型试验和数值分析两种方法。物理模型试验是通过ADV流速仪或PIV流速仪监测桥墩处水流特性，结合激光诱导荧光技术及染色法使测量结果更准确[7]；数值模拟是采用(LBM)[8]、RANS[9]、LES[10]等方法模拟柱体绕流问题。刘晓平等[11]研究得出横流影响船舶航行的横漂速度、航迹线宽度、漂角等，船舶在受到横流作用，容易改变航线，加大船桥碰撞概率，研究船舶航行经过桥墩的过程，合理规划航线，能够降低船撞风险。乾东岳等[12]利用动网格技术探究桥墩周围紊流对船舶的干扰，分析船舶经过桥墩时，受偏航力矩，船舶发生运动，提出安全船墩间距跟船舶大小、桥墩类型有关。牛国杰等[13]采用物理模型试验研究桥墩附近流场影响船舶航行，船墩间距较近时，船舶艏摇力矩会正负交替变化。柯兴[14]揭示了墩前横流分布规律，不同船速驶过桥墩时的受力特点，得出船速越大，船舶偏航角变化越小，对船桥交汇有指导作用。目前，关于斜交桥梁布设防船撞装置对船舶航行的影响研究较少，故进行斜交桥墩布设防撞装置影响通航研究具有重要的实际意义。

为研究船舶在经过特定桥区时的受力变化，采用RANS法模拟高雷诺数下桥墩绕流。基于二维N-S方程理论，利用有限体积法[4]，求解离散方程，采用动网格技术，由FLUENT中的自定义函数UDF来模拟船舶运动，探究桥墩设防防撞装置类型、斜交角、船桥间距对船舶运动形态及受力变化的影响，研究船舶在不同因素影响下的船舶艏摇力矩的变化，初步确定特定条件下的安全船墩间距，为解决船舶安全通航问题提供参考。

1 模型建立及验证

1.1 控制方程及数值解法

因湍流RNGk-ε模型在船舶CFD应用广泛，计算量适中，精度较好，故在对桥区水流形态的模拟采用RNGk-ε建立数学模型。湍流RNGk-ε模型[15-17]是基于RANS法，结合涡粘模型和两方程模型，能够准确模拟完全湍流流动，它的基本思想是通过在任意空间尺度上的一系列连续的变换，对原本十分复杂的系统或过程实现粗分辨率的描述。标准的k-ε模型变形方程和系数来自解析解，在ε方程中改善了模拟高应变流动的能力。

k-ε方程为：

(1)

(2)

(3)

(4)

其中:k为湍流动能；ε为湍流耗散率；Gk=0.99，为平均速度梯度引起的湍动能k产生项;μ为湍动黏度;δk=1.0；C1ε=1.44；C2ε=1.92。

由于有限体积法效率高，适应性强，支持并行计算，故采用此方法来进行求解计算，压力方程用加权体积力形式求解，动量方程用二阶迎风形式求解，湍动能和湍流耗能率方程采用一阶迎风形式求解。

1.2 模型建立

根据长江通航河段典型桥梁形式，选取的涉水桥墩为双薄壁墩形式，设防方式根据工程实际情况及《桥梁防撞理论和防撞装置设计》，选择常见的圆艏型和尖艏型防撞装置进行设防，装置长为31.2 m，宽为18 m，如图1所示。如图2所示，防撞装置与水流流向的斜交角分别为0°、10°、20°、30°。根据文献研究成果[18]，为使水流来流稳定，确定计算域宽为200 m，长度为700 m。如图3所示，桥墩布置处距离入口边界200 m，距离出口为500 m，距离左边界150 m，距离右边界50 m,岸线和桥墩均为壁边界，模拟水流速度选取嘉陵江常年平均流速为2.3 m/s。船舶选用嘉陵江代表船型：1 000 t级驳船，其尺寸大小为67.5 m×10.8 m×2.0 m，吃水深度为1.2 m。船舶航行的纵向范围(船重心至墩轴心的纵向距离)为-2L～5L(L为船长)，选取1 000 t驳船在嘉陵江上的正常平均航行速度为2.7 m/s，图3为动船模型布置图，其中，B为船舶边缘到桥墩边缘的距离，即船墩间距。

图1 桥墩及防撞装置模型示意图

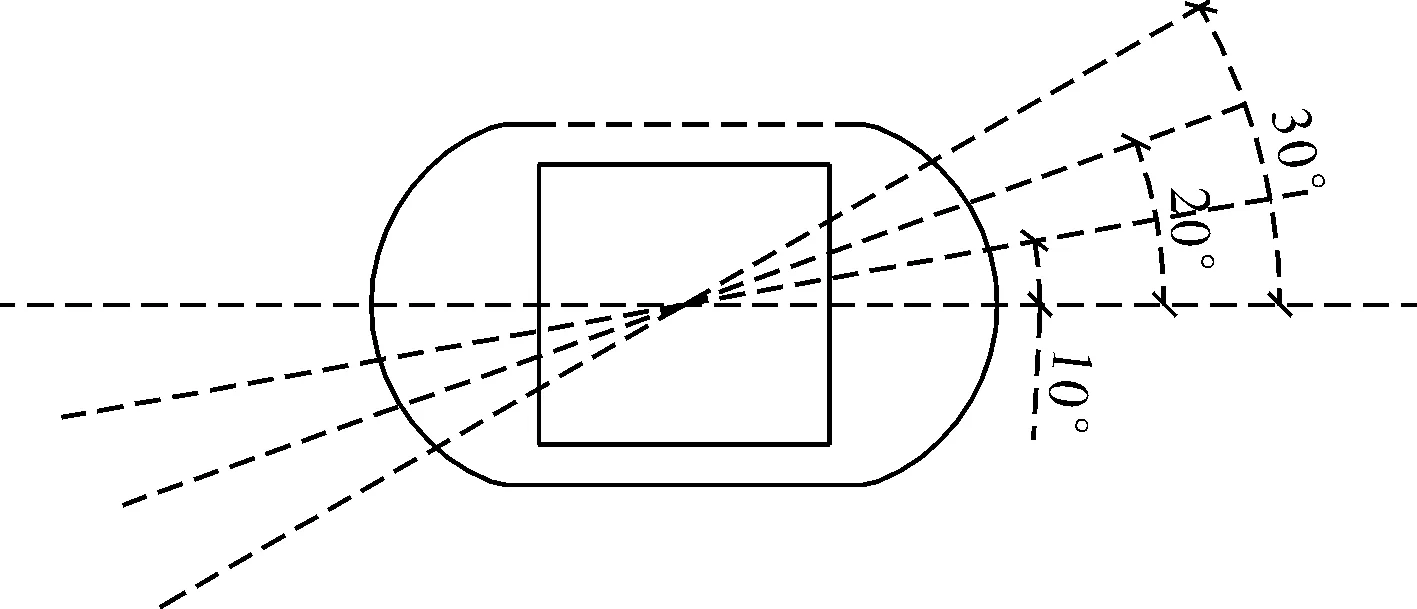
图2 模型工况示意图

图3 动船模型布置图(单位:m)

入口边界条件：指定计算域左侧为速度入口，X方向流速为2.30 m/s，Y方向流速为0，流速均匀分布；出口边界条件：指定计算域右侧为自由出口；边壁条件：桥墩设防前后的壁面、船舶的轮廓线以及计算域壁面设置为无滑移壁面，各个壁面上各个网格节点的速度均为0。船舶运动方向为顺流而下，运动速度为U=2.7 m/s。

在模拟船舶经过桥墩模型中，船舶的平面运动可以视为三自由度问题，为解决船舶位移与网格尺寸相差较大引起的不收敛问题，采用弹簧近似光滑模型和局部重剖分模型对动网格区域进行网格更新。由于三角形网格非常适合于2D动网格，故以三角形结构划网格剖分计算域。根据模型绕流的模拟经验，桥墩周围的网格尺寸需加密处理，网格尺寸应远小于涡的直径。桥墩、船舶的边壁需要进行加密处理，船舶运动区域需要保持均匀的网格，其余区域系统平滑过渡。其中网格最大尺寸为15 cm，共计7 974 100个单元，整体网格划分如图4所示。局部加密的网格划如图5所示。

图4 动船模型网格划分示意图

图5 网格局部加密处理

1.3 模型验证

(1) 绕流水力特性验证。圆柱绕流水利特性验证可以通过雷诺数Re、升力系数Cl、阻力系数Cd以及斯特劳哈尔数St来体现。本文在所有工况的研究中，保持雷诺数一致，取Re=3.60×104，由于篇幅有限，以桥墩布设圆艏型防撞装置、斜交角为0度工况为例，将计算结果中的Cd与Igarashi[19]的试验及数值模拟计算成果进行对比，如表2和图6所示。通过对比发现，两者的曲线变化规律一致，数据吻合较好。

表2 圆柱绕流计算结果对比

图6 桥墩图阻力系数历时曲线图

(2)绕流流场特性验证。为了进行流场特性验证，进行物理模型试验，采用塑料示踪粒子和XKVMS-02大范围表面流场测量系统测量桥墩周围表观流态分布。限于篇幅，以斜交角为10°，桥墩设防圆形防撞装置工况为例，物理模型试验流场分布和数值模拟流场分布如图7所示。对比图7(a)和图7(b)可知，水流流经桥墩附近时，受到桥墩的阻水作用，桥墩附近流速增大，尾部由于流速较小，少有示踪粒子的分布。数值模拟和实验观测结果较为相近。

图7 斜交角为10°，设防圆艏型防撞装置时流场分布图

2 模拟分析

船舶顺水航行的工况分析步有2 200步，时间步长为0.05 s，船舶顺水流航行，从开始航行到结束共计110 s，船速为5.0 m/s(大地坐标系)，航行距离为550 m，整个计算域长度为700 m，船舶出发位置在桥墩上游处120 m。图8为船舶经过桥区过程中的受力分析图。

2.1 桥墩设防方式对船舶航行的影响分析

图9是船墩间距为18 m时，桥墩在未设防、设防圆艏型防撞装置、设防尖艏型防撞装置时的船舶艏摇力矩曲线图，其中横轴为水流顺流方向，纵轴为船舶艏摇力矩，正的峰值表示船舶向靠近桥墩一侧偏转，负的峰值表示船舶向远离桥墩一侧偏转。从图9可以看出，桥墩设防后还是会出现三个艏摇力矩峰值，这与柯兴[14]所获得的船舶艏摇力矩规律大致相同。设防前后船舶艏摇力矩变化规律几乎相同，但是峰值出现位置有略微改变，设防后力矩开始突变位置早于未设防时，原因是由于防撞装置几何尺寸较大，设防后造成的绕流效果早于桥墩设防之前；第1负峰值出现位置设防圆艏型防撞装置早于桥墩未早于设防尖艏型防撞装置，正峰值出现位置是设防前早于设防后，第2负峰值是设防后早于设防前。

图8 船舶经过桥区过程中的受力分析图

图9 船墩间距为18 m时船舶艏摇力矩历程曲线图

从表3可知，船墩间距为18 m时，设防后三个力矩峰值均成倍增加，未设防前曲线变化幅度为-1 549.5 N·m～1 050.8 N·m，船舶受到一定的影响；圆艏型设防后曲线变化幅度为-3 098.6 N·m～1 897.4 N·m；尖艏型设防后曲线变化幅度为-3 150.1 N·m～2 020.1 N·m；设防后较设防前船舶受到的艏摇力矩更大，对船舶航行的影响更大，且尖艏型的影响大于圆艏型，当桥墩设防后，船舶通航所需的安全航行间距应相应增大。

2.2 斜交角对船舶航行的影响分析

从2.1节分析可以得到，尖艏型设防对船舶航行的影响最大，图10为该设防形式下斜交角与船舶力矩的变化规律。可以看出，船舶在桥墩附近存在3个艏摇力矩峰值，且第1负峰值点和正峰值点位置不随角度的改变而发生变化，第2负峰值点位置随角度的改变而发生变化但无明显的规律。随着斜交角的增大，船舶经过桥区时所受的艏摇力矩也增加，斜交角与第1负峰值绝对值和正峰值成正相关关系，第1与第 2负峰值变化规律不相同，而正峰值变化规律基本一致，艏摇力矩随斜交角增大逐渐按比例增大．斜交角从0°变化为10°时艏摇力矩变化最大，如表4所示．随斜交角增大，第1负峰值也增大，而第2负峰值随斜交角增大力矩没有明显变化规律，斜交角为0°和10°时约为1.1 kN·m，但斜交角为20°和30°时分别约为0.61 kN·m和0.7 kN·m。从表3和表4中艏摇力矩的增量可知，桥墩设防对船舶航行的影响大于斜交角的影响。

表3 桥墩间距B为18m时桥墩设防前后船舶艏摇力矩峰值

图10 桥墩间距B为18 m时设防尖艏型防撞装置后不同斜交角船舶艏摇力矩曲线图

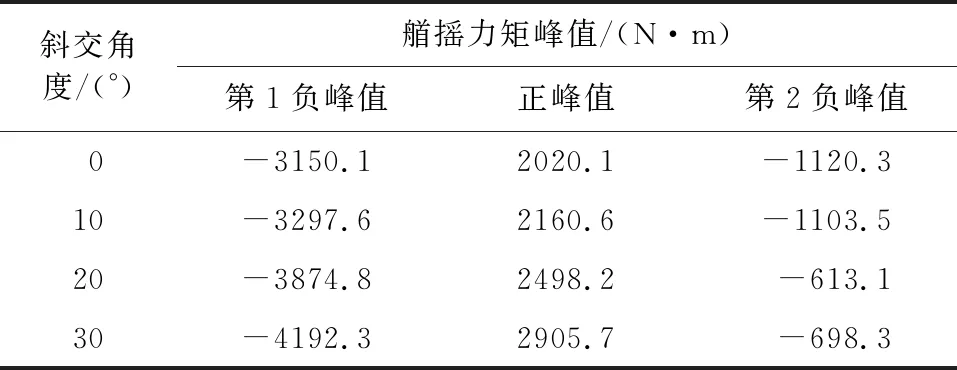
表4 桥墩间距B为18 m时设防尖艏型防撞装置后不同斜交角船舶艏摇力矩峰值

2.3 船舶与桥墩距离对船舶航行的影响分析

图11为斜交角30°(最不利角度)时桥墩设防尖艏型防撞装置后不同船桥间距下船舶艏摇力矩的变化曲线。当B为18 m～54 m时，在船舶靠近桥墩-驶离桥墩-远离桥墩，有三个较为明显的峰值，且出现位置不随桥墩间距变化而发生明显改变。由表5可知，B为18 m～54 m时，随着间距增大，第一负峰值和正峰值大幅度减小，第二负峰值同样减小，但变化幅度不大。当B为18 m时，从-4 458.2 N·m变化到3 601.5 N·m,此时防撞装置对船舶航行的影响较大。当B为54 m时，从-1 071.7 N·m变化到571.9 N·m，防撞装置对船舶航行的影响较小。

图11 斜交角30°时不同船桥间距下船舶艏摇力矩变化曲线

表5 不同船墩间距下艏摇力矩峰值

为了分析船舶在设防桥墩附近运动时产生的运动形态的原因，按照1∶100模型进行了船模试验，见图12，观测船舶在不同船墩间距下的船舶航行轨迹线，采集视频进行处理，将得到特定时刻船舶的位置进行标志，通过读取像素点反馈在试验选取坐标系中，绘制成图，如图13所示。

图12 船舶航行的航迹线示意图

结合图11和图13，对比分析船舶在特定位置下的船舶运动形态和艏摇力矩，产生船舶运动形态的原因有：第一个峰值为船舶船艏驶至桥墩，船舶在不断靠近桥墩这个过程中，船速较水流流速快，船艏部分水流阻挡，水流受到挤压，桥墩上游产生紊流，横流速度较大，对船舶有外推作用，所以船舶在桥墩上游靠近桥墩过程中会出现第一个峰值；第二个峰值是船舶驶至桥墩中部时刻。船舶受桥墩绕流得到影响，附近的水流向桥墩尾流区转向流动，且桥墩尾流存在负压，船艏受到吸引，向桥墩一侧偏转，重心过此处，达到最大值；第三个峰值是船尾驶离桥墩，进入桥墩下游的负压区，使得船尾向靠近桥墩一侧偏转，导致船艏向远离桥墩一侧偏离，所以形成第三个极值点。此外，船舶船尾驶离桥墩后，船艏力矩略有波动且力矩大小接近0，这是船舶航行至桥墩尾流区受到桥墩尾流的影响。在流速2.3 m/s和船速为2.7 m/s条件下，船舶经过桥区时B大于54 m(3倍装置宽度)所受到水流干扰影响较小，可判定为船舶安全航行间距。

图13 斜交角30°时不同船桥间距下的船舶航迹线图

3 结 论

(1) 桥墩布设防撞装置对船舶航行的影响很大，为了尽可能的减小对船舶航行的影响，必须进一步对防撞装置的尺寸、外形等优化，保证船舶航行的安全。

(2) 船墩间距、桥墩设防方式相同时，斜交角越大，船舶转向的特征艏摇力矩幅值越大，船舶偏转越厉害。当斜交角与桥墩设防方式相同时，船墩间距越大，船艏受到的艏摇力矩值越小，对船舶航行的影响越小。对比这两个因素的影响，船墩间距减小比斜交角增大更加不利于船舶的安全航行。

(3) 在最不利设计工况下船墩距离为54 m(3倍装置宽度)时，船舶航行所受的艏摇偏转力矩较小，可以视为几乎没影响，故船墩间距为54 m时可以初步定为船舶经过布设防撞装置的斜交桥墩时安全航行的安全船墩间距。