大规模水电系统优化调度维数灾问题研究进展

冯仲恺，牛文静，程春田，周建中，张勇传

（1．河海大学水文水资源学院，江苏省南京市 210098；2．长江水利委员会长江水文局，湖北省武汉市 430010；3．大连理工大学水电与水信息研究所，辽宁省大连市 116024；4．华中科技大学土木与水利工程学院，湖北省武汉市 430074）

0 引言

我国水电行业近年来发展迅猛，相继建成投产了乌江、澜沧江、红水河等数个装机容量达千万千瓦级的特大流域水电基地，形成了调蓄能力强、装机规模大、电站数目多、辐射范围广的大规模互联水电系统[1-3]。为助力实现“碳中和、碳达峰”战略目标，我国积极推进西南地区多个大型水电基地建设开发工作，使得体量巨大的水电系统在未来很长时间内持续扩张；同时，水利电力系统管理要求日趋精细，对水电调度计算的时效性、精确性、互动性等方面要求随之增高。因此，伴随系统规模及其运行复杂性的持续攀升，大规模水电系统优化调度面临日益严峻的维数灾问题，以往的中小规模梯级调度建模求解思路难以适用，亟待在经典水电调度理论基础上不断探索科学有效的降维优化方法[4-6]。为此，本文在深入分析我国大规模水电调度维数灾成因基础上，概要总结了国内外最新研究进展并给出未来可以进一步深化研究的方向建议，以期为我国现在乃至未来更大规模的水电调度提供有益理论参考。

1 快速发展的大规模水电系统

经过数十年的快速发展，我国水电系统规模远超其他水电大国，在区域电网、省级电网、特大流域、巨型电站、发电机组等多个层面均取得了巨大突破，形成了世界水电史上前所未有的大规模多层级水电系统。与此同时，为促进电源侧清洁替代和消费侧电能替代，我国大力推动以西电东送为典型代表的重大战略工程，着力将西部优质水电通过特高压输电网络输送至中东部沿海负荷高峰中心，进一步加剧了水电调度复杂性。在此背景下，大规模水电系统开展调度作业时，既要考虑发电、防洪、供水、灌溉、航运等综合利用需求，又要考虑区域内外协同管理、梯级上下游联合调控、电站与机组安稳运行等时空耦合约束，还要考虑调管权限层级划分、并网节点拓扑解析、多边电力协议、输电线路容量等多级运行限制[7-9]。图1为水电调度复杂性示意图。可以看出，金沙江各电站分别由不同发电集团调管，如何在兼顾城市供水需求的同时实现跨部门合作共赢是复杂调度难题；金安桥和小湾水电站分别面临特殊的孤岛运行与非规则振动区问题；溪洛渡需要同时送电多个电网，面临前所未有的一库两调需求；向家坝需要兼顾防洪、灌溉等综合利用需求；景洪—橄榄坝需要均衡电网调峰需求与河道通航目标，反调节问题突出；更为棘手的是，间歇性能源电站（如风电、光伏、小水电）与大中型水电站通过不同节点、不同电压、不同线路向多个电网同时提供电力电量，呈现复杂的异构并网特征，协调难度远超传统集中并入单一电网。

图1 水电调度复杂性示意图[5]Figure 1 Sketch map of the hydropower operation complexity [5]

2 大规模水电系统优化调度维数灾问题

随着系统规模及其运行复杂性的持续攀升，大规模水电系统优化调度面临日益严峻的维数灾问题[7-9]，集中体现在运算时间过长（超出调度时限要求）与内存占用过多（超出计算机容量极限）等方面，其原因在于以下几个方面：

（1）水电系统固有的动态、非线性等调度特征使得求解方法选择受限。一方面，除受到调度期内各阶段区间径流、电网负荷等因素影响外，水电还会在很大程度上受到火电、风电等其他能源调度方案的影响，这就要求调度方法具有良好的交互性、能够快速响应计划执行偏差。如图2所示，除基础特性曲线（如水位—库容、尾水位—下泄流量）外，水电调度目标与约束条件大多为决策变量的非凸、不连续函数，在调节计算过程中若强行进行线性化处理极易引发模型失真、结果偏差较大等问题。因此，为保证结果的时效性、实用性与可靠性，线性规划、非线性规划、智能算法等在实际工程中应用相对较少，大多选用动态规划及其改进算法（如离散微分动态规划、逐步优化算法）。

图2 水电调度非线性特征示意图[3]Figure 2 Sketch map of the hydropower operation nonlinear feature [3]

（2）庞大的系统规模使得水电调度维数灾问题愈加凸显。一方面，受单站规模（如装机容量、库容、水头）扩大影响，各电站在相同离散精度下的决策变量数目必然增多，例如，若按1m对水头进行离散，则高坝大库可能有数百个状态，远多于常规低水头电站；另一方面，系统维数与求解难度会随着计算电站数目的增多而显著增加，如N座水电站的状态均离散k份，则单阶段的离散状态组合数目为kN，使得系统计算规模与搜索空间均呈指数增长，此时每增加1座电站，水电调度运算量与存储量至少扩大k倍。从图3可知，随着电站数目的增大，系统计算压力骤增、维数灾问题凸显。现阶段，我国流域梯级和省级电网水电系统需要统筹数十座电站，严重超出传统水电调度算法的计算极限。

图3 水电调度计算开销示意图[3]Figure 3 Sketch map of the hydropower operation computational overhead [3]

（3）多重复杂约束又进一步加剧了水电调度维数灾问题。水电系统通常需要均衡考虑水利、电力、环保等相关主体的利益诉求，以及机组、电站、流域和电网等多层级运行限制，使得在开展联合调度时会面临数目众多、形式各异的约束条件集合：既有以水位限制、出力限制、流量限制为代表的不等式约束，又有以水量、流量、电量平衡方程为代表的等式约束，还有以机组启停状态、出力持续时段为代表的混合整数约束。从图4可知，各项约束彼此存在着不同程度的耦合作用，使得水电调度决策空间呈现复杂的跨时空关联特征，各电站在时段j-1运行状态的微小改变都有改变时段j的可行决策空间，进而导致自身或相邻电站后续关联时段约束条件的破坏，极大影响了寻优效率与搜索精度。

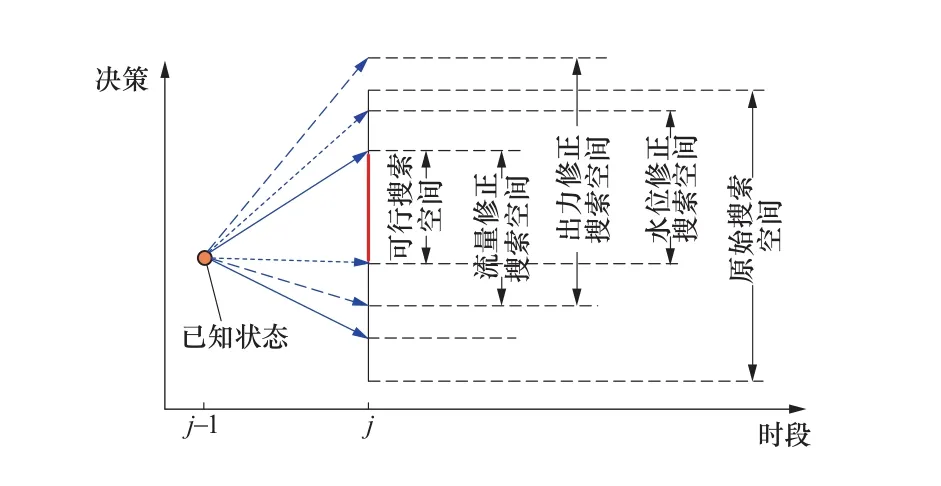
图4 水电调度约束时空关联特征示意图[3]Figure 4 Sketch map of the hydropower operation spatial-temporal constraints [3]

3 大规模水电系统优化调度维数灾问题研究进展

作为典型的多阶段多变量约束优化问题，水电调度自20世纪50年代起便受到了国内外从业人员的普遍关注，经过多年系统深入研究，大致形成数学规划和智能算法两大类方法[10-12]：前者以线性规划、非线性规划、动态规划及其改进方法、拉格朗日松弛为代表，在实际工程中应用相对广泛；后者主要有人工神经网络、遗传算法、模拟退火、粒子群算法、蚁群算法、差分进化算法、混沌优化算法等，更多地侧重于理论研究。总体来看，现有水电调度算法已在工程实践与理论研究取得了不同程度的成功，但是仍然存在结果失真、耗时过长、开销过大等局限，依靠单一优化算法难以支撑我国大电网平台下水电调度实际需求。为缓解维数灾问题，国内外研究人员从多个角度出发，对现有水电调度方法实施改进或利用新的技术手段来构建新型优化方法，应用规模也经历了从单库到多站、从梯级到流域、从跨流域到跨省区的发展历程。根据笔者对近年来发展动态的理解与认知，相关理论思想主要集中在系统规模精简[13-15]、复杂约束处理[16]与优化求解方法[17]等三个方面，接下来进行详细介绍。

（1）在系统规模精简方面，可将已有研究大致分为以下三类：一是参与计算电站集合精简，如聚合水库法、轮库迭代法、流域分级法、分区优化法等；二是电站基础特性与目标函数的简化，如（分段）线性化或多项式拟合电站的特征曲线、边际效用递减假定等；三是计算阶段与离散状态等层面的精简，如逐步优化算法、离散微分动态规划、逐次加密动态规划等。这些简化手段虽然能够有效降低算法计算难度、减轻存储压力，但由于对水电调度原型问题做了一定的概化、近似处理，使得优化结果存在不同程度的偏差。以聚合水库法为例，该方法根据水文或地理特征、水力和电力联系将水库群聚合成为等效虚拟水库进行优化计算，而后采用条件期望分解法等手段将所得聚合库容和聚合来水量在空间上分配，这种方式在很大程度上简化计算，但其聚合过程通常假定水头是恒定不变的参数，导致所得等效水库忽略了梯级水库间的水头效应差异，且聚合、分解过程中所参照规则往往由人工经验制定的，容易引发计算偏差，仍然存在较大改进空间。因此，需要进一步研究如何利用领域知识科学削减水电调度规模，以达到有效减少系统维数的目的。

（2）在复杂约束处理方面，可将已有研究大致分为以下四类[3，19]：一是惩罚函数法，主要在目标函数中考虑约束违反程度以实现“优胜劣汰”，具有形式简单、可操作性强等优点，但是不同约束破坏对应的惩罚系数选取较为困难，通常需要考虑问题特征进行确定、工作量相对较大；二是方案修复法，将非可行调度方案通过预设规则或策略调整至可行空间，能够在很大程度上保证解的可行性，但是修补策略需要根据目标函数、约束条件等模型特征动态调整，增大了计算量和存储量；三是多目标法，将约束破坏项视为特定目标以便利用Pareto占优机制识别个体优劣，但是难以保证最终方案的可行性；四是约束集成法，将约束条件转化为决策变量对应的等效约束，虽然能够改善算法性能，但是难以集成处理复杂非线性约束、有待深化相关工作。因此，需要进一步研究如何利用复杂约束特性来辨识可行搜索空间，以达到减少冗余开销的目的。

（3）在优化求解方法方面，相应的研究工作可大致分为以下三类：一是引入计算机领域的前沿技术，对传统方法实施并行化设计，以利用现有机器丰富的并行资源来获得良好的计算加速效果，例如并行动态规划、并行离散微分动态规划、并行遗传算法等，此类方法虽然能够有效缩短计算时间、提高资源利用效率，但一般对算法空间复杂性改进有限、求解规模仍然受制于原有算法技术瓶颈，未能从根本上解决维数灾问题；二是利用经济学原理、最优化方法等相关理论解析所求问题的数学特性，以期减少无效状态的冗余计算，例如改进动态规划、两（多）阶段搜索算法等，此类方法能够有效降低计算量、提高收敛速度，但是大都需要某些特定的物理假设（如优化目标为凹函数）、且解算规模普遍偏少（如单一水库或并联水库群），而水电调度不同目标的数学表达形式及其性质差异很大，难以直接采用此类算法进行求解，如何提高理论的普适性与通用性有待进一步研究；三是引入其他学科理论或耦合多种算法优势改善现有算法性能表现，以降低算法计算复杂度、缓解维数灾问题，如均匀动态规划、多层嵌套动态规划、强化学习与混合策略等，虽然这些算法的有效性通过应用检验，但在大规模水电调度问题的适用性和完备性有待检验。因此，需要进一步研究如何集成跨学科知识构建新型优化算法，以达到科学求解大规模水电调度问题的目的。

由此可见，已有研究虽然取得较为丰硕的理论成果，但无论电站数目还是运行复杂性与我国水电系统实际情况存在一定距离，在应对超大规模复杂水电系统维数灾问题时仍然存在不同程度的局限，因而十分有必要在深入分析已有成果基础上，继续探索和创新具有工程实用性与科学完备性的大规模复杂水电调度降维理论方法，以切实满足我国水电调度计算建模需求。

4 大规模水电系统优化调度维数灾问题应对策略

从数学上看，水电调度可归属为典型的大规模多变量约束优化问题，其解算形式可抽象为，其中opt表示最优，可以是min、max等算子；f表示系统优化目标，如发电量、发电效益等；S为复杂约束集合，如水量平衡方程、水位运行限制等；x为待优化变量，如各电站在调度期内水位过程；另一方面，现有水电调度算法大都运用逐次逼近理论，从某个初始解x0出发迭代计算获得满足复杂约束集合S的调度方案，可采用刻画对应的寻优过程，其中m表示不同优化方法、k表示迭代次数。因此，从数学角度出发，未来可以深入研究调度知识挖掘以快速生成初始解x0、决策空间辨识以满足约束集合S、高效寻优机制m以实现提速增效等内容，为丰富和完善我国超大规模水电调度理论体系提供有益研究建议和思考，具体内容如下：

（1）调度知识挖掘以提升初始调度方案质量。考虑到运用计划与实际运行数据能够有效反映水电调度工况信息，而一线调度人员丰富的工程经验能够直接体现人工对水电运行状态的预判指令与决策信息[18，19]，因而可以构建基于海量多属性数据的水电调度知识规则库，从而根据管理层级、优化目标、区间径流等工况信息快速确定初始调度过程并适当削减参与计算电站数目，从而在降低系统规模的同时提高算法效率与结果实用性。

（2）决策空间辨识以有效降低模型计算测度。大规模水电系统优化调度通常面临形式各异、紧密耦合但彼此之间又难以定量解析的复杂约束集合，使得调度决策空间形态复杂多变、“黑箱”特性明显，导致优化算法极易陷入局部最优、甚至难以获得可行的调度方案，因此可从决策空间辨识角度出发[20]，动态判别系统在调度期内的可行决策空间，降低非可行解的冗余计算开销，以便减少甚至避免无效状态的存储与计算，切实提高算法寻优性能。

（3）高效寻优机制以实现解算过程的提速增效。考虑到常规算法大多需要处理所有潜在状态组合及其指标值等信息、导致所需计算开销随系统规模扩张呈非线性增长，因而可以从算法搜索机理角度出发，构建有效均衡求解精度和计算效率的实用降维解算方法。例如，可以深入研究动态规划类算法状态变量精简方法以降低算法计算开销，或者基于空间响应曲面的代理优化算法以降低计算频次，抑或引入新的算法以提供新的可能[21]，抑或研发全新搜索机制以提高寻优效率[22]。

5 结论

伴随水电系统规模持续快速扩张，如何破解维数灾、实现水电调度的科学建模与高效求解一直是水电调度领域相关从业人员的前沿科技难点与热点问题；为应对近年来日益严重的环境与能源危机，国内外相关机构与部门更是进一步加大了对大规模复杂水资源系统联合调度问题的关注与投入。为此，本文结合笔者长期研究思考，概要介绍了我国快速发展的大规模水电系统，分析了维数灾问题产生根源并总结了国内外相关研究进展，进而从数学角度给出了水电调度高效降维策略，目的是在合理计算开销下快速获取高质量调度结果，为我国水电等清洁能源系统的安全经济运行提供理论支持。