某混凝土重力坝强震损伤特性的振动台模型试验研究

高建勇 ，许亮华 ，胡 晓

（1．中国水利水电科学研究院工程抗震研究中心，北京市 100048；2．水利部水工程抗震与应急支持工程技术研究中心，北京市 100048）

0 引言

目前，我国在西部强震区修建了一批特高坝，大坝建设和运行期经历强震的风险很高[1]。为了指导大坝结构经历强震后应急抢险，降低或消除次生灾害，非常有必要对大坝结构在震时进行损伤判断、震后进行有效的损伤检测，尽快判断震害位置和程度，使结构能得到及时修复和加固，从而确保大坝安全可靠。

大坝损伤识别的普遍做法是在大坝结构的关键部位埋设各类智能传感器，通过实时监测与分析，并应用模态识别理论对大坝结构的损伤进行诊断。近十几年来，国内外学者主要围绕损伤识别指标和识别算法两个方向，对大坝结构损伤理论进行了大量研究，取得了很多富有价值的研究成果。其中，在损伤识别指标的确定方面，胡晓等[2]选用频响函数虚部的变化对大坝损伤的部位进行动力诊断；牛婷婷[3]采用应变模态组合指标法识别出坝肩失稳损伤所在的方向；邹浩[4]提出了利用压电陶瓷传感器对混凝土结构的应力及内部损伤进行探测的方法。

在损伤算法研究方面，吕玮等[5]利用径向基函数神经网络对重力坝损伤位置和损伤程度进行研究；廖群[6]对基于神经网络的无迹卡尔曼滤波算法应用于高拱坝损伤识别的可靠性和鲁棒性进行了研究；程琳等[7]基于强震观测，提出采用矢量自回归滑动平均模型和稳态图法来进行混凝土坝结构模态参数识别；姚尚武等[8]基于最小频率误差方法对混凝土重力坝的损伤部位进行识别；D. Hamidian等[9]基于小波变换和自适应模糊神经推理系统（ ANFIS ），对规则的大坝进行损伤识别。

但是这些方法要进入真正的实际应用还需要进行很多理论研究工作。本文以国内某混凝土重力坝为原型，通过振动台模型破坏试验，对大坝在超载地震下的损伤形态以及损伤演进规律进行了研究，对损伤判别方法进行了探索，为大坝动力诊断提供了技术参考。

1 振动台模型

1.1 原型概况

本试验以国内某碾压混凝土重力坝为原型，最大坝高120.34m，坝顶长736.00m，设计总库容为5.7亿m3，库区水面12km2，大坝设计地震烈度为Ⅷ度，对应水平峰值加速度为0.20g。该工程在2008年5月12日汶川地震时，由于紧邻震中区并且正处于施工高峰期，地震造成已浇筑的大坝出现11处贯穿性裂缝[10]。

由于混凝土重力坝坝轴线较长，而横断面较小，对于远离坝肩的坝段可以按平面应变问题进行考虑。本次试验模型选取该重力坝的一个坝段，通过在顺河向输入超载地震进行损伤形态以及损伤规律的振动台试验研究。

1.2 振动台模型

通过对该重力坝坝段进行有限元计算，得到大坝前两阶固有频率分别为2.44Hz和4.96Hz。

根据振动台台面尺寸，选取几何相似常数为1/120，并通过一系列不同龄期、不同配比的微粒混凝土材料试验，最后确定大坝模型材料：选用13天龄期左右的1：6：0.5：1.14（水泥：砂：石膏：水）的混合砂浆来制作重力坝坝段振动台模型，得到弹性模量相似常数：Sσ=SE=0.3。模型材料开裂峰值拉应变约为80με。由于要模拟坝段模型弹塑性损伤演变，因此应变相似常数取 Sε=1。

基于相似常数，设计并制作了几何相似常数为1/120的重力坝坝段模型，其中动水压力基于修正的Westergaard 模型，以附加配重的形式施加。

2 模型测点布置与试验工况

本次试验共布置单向加速度传感器11个，单分量应变片3个，三分量应变花6个，总通道32个。

2.1 加速度测点

振动台台面沿X向布置1个加速度传感器，实测台面输入；模型底板表面沿X向布置2个加速度传感器，实测模型基础加速度；沿大坝模型不同高程关键位置分别布置8个加速度传感器，用于测定模型加速度沿高度的放大及其平动与扭转振型。加速度传感器布置如图1所示。

图1 加速度传感器布置图（单位：mm）Figure 1 Arrangement of acceleration sensors（unit：mm）

2.2 应变测点

在坝踵、坝趾以及坝折坡点下游坝面应力集中区域布置应变花、应变片，实测模型关键部位的动应力，应变片布置图，参见图2所示。

图2 应变测点布置图（单位：mm）Figure 2 Arrangement of strain gauges（unit：mm）

2.3 试验工况设置

根据《水电工程水工建筑物抗震设计规范》（NB/T 35047—2015）的规范谱[11]，拟合得到人工地震波作为原波，根据相似常数缩比得到模型人工地震波，沿水平（顺河）向进行激励，并逐级增大激励波的幅值，对模型的损伤破坏过程进行研究。主要试验工况有：

（1）白噪声（120s）探查试验，对结构模态特性进行探查。

（2）振动台模拟地震试验，逐级增大模型人工波幅值进行水平（顺河）向激励。包括：1/3倍设计地震、设计地震、1.5倍设计地震、1.8倍设计地震、2倍设计地震、1.8倍设计地震场地波。

（3）实测不同工况下模型的动力特性及动力响应，通过相似关系换算得到原型结构在不同水准地震作用下的动力响应。

具体工况见表1。其中，通过W1工况扫频得到模型结构空库下的频率（模型未加配重质量），根据自振频率修正模型相似比尺；W2工况扫频得到模型结构满库下的初始模态特性（模型施加配重）；W3～W8扫频得到模型结构满库下经历不同水准地震工况前后的模态特性，根据模态参数的变化对结构的损伤演变规律进行研究。

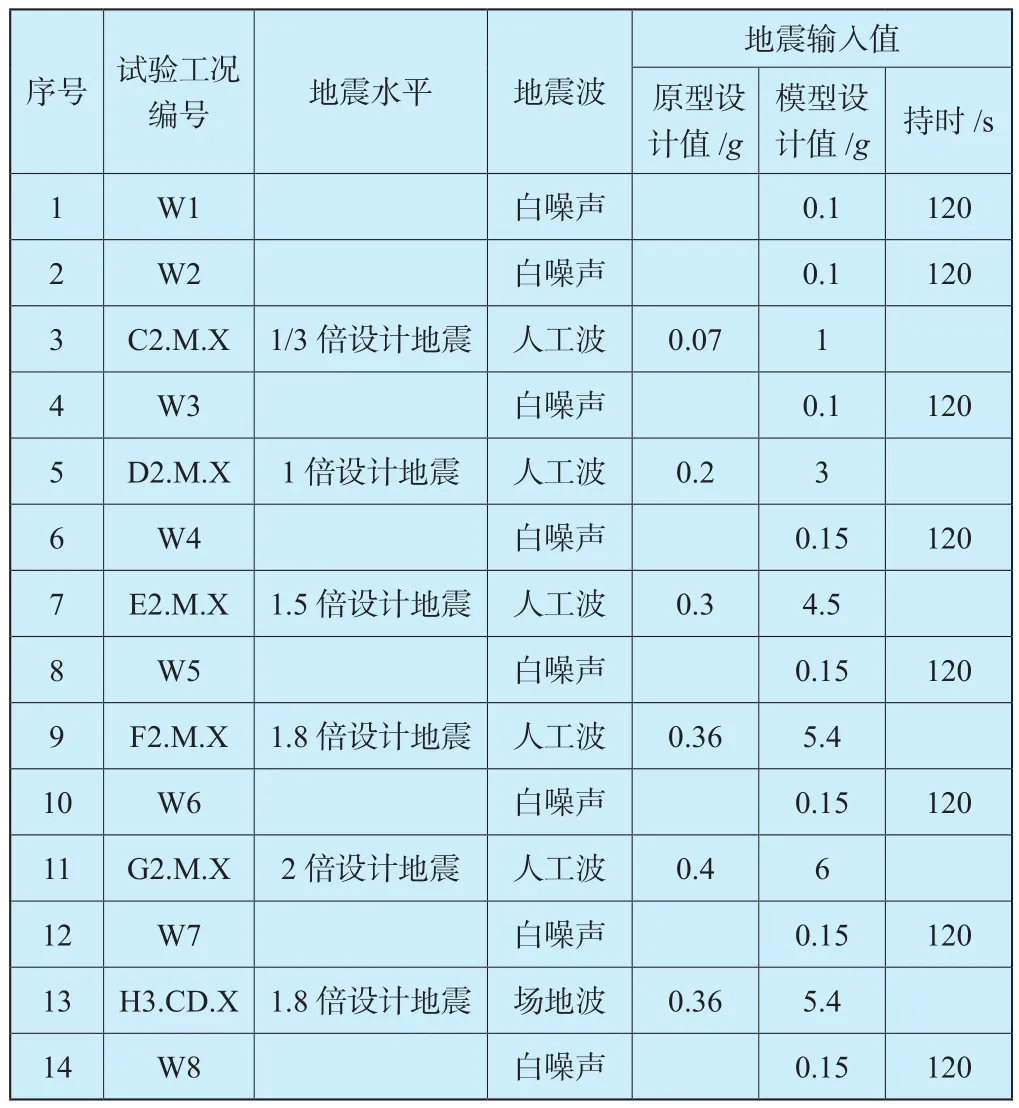
表1 振动台模型试验工况Table 1 Conditions of shaking table test

3 试验结果与分析

3.1 模型损伤破坏概况

在1/3倍设计地震下，人工波激励后，坝段结构未见裂缝，结构整体处于弹性阶段。

1.0倍设计地震至1.5倍设计地震阶段，人工波激振后，坝体折坡点出现微小裂缝，折坡点处应变值虽然已经达到开裂应变，但是用肉眼很难发现裂缝，模型整体仍处于弹性阶段。

经过2倍设计地震人工波激振工况后，模型折坡点拉应变值超过开裂应变，外观可见细小裂缝，但裂缝并未贯穿。

在1.8倍设计地震场地波激振下，模型的折坡点裂缝已从上游折坡下部向下游曲面连接段贯通发展，出现明显损伤破坏现象，见图3，但折坡点以下坝体依然保持完整状态。

图3 模型折坡点的贯穿裂缝Figure 3 Through cracks in the neck of the model

3.2 应变及破坏情况

在各级顺河向地震波激振下，大坝关键部位的最大拉应变结果列于表2。根据应变相似常数得到原型材料的开裂峰值拉应变约为80με。

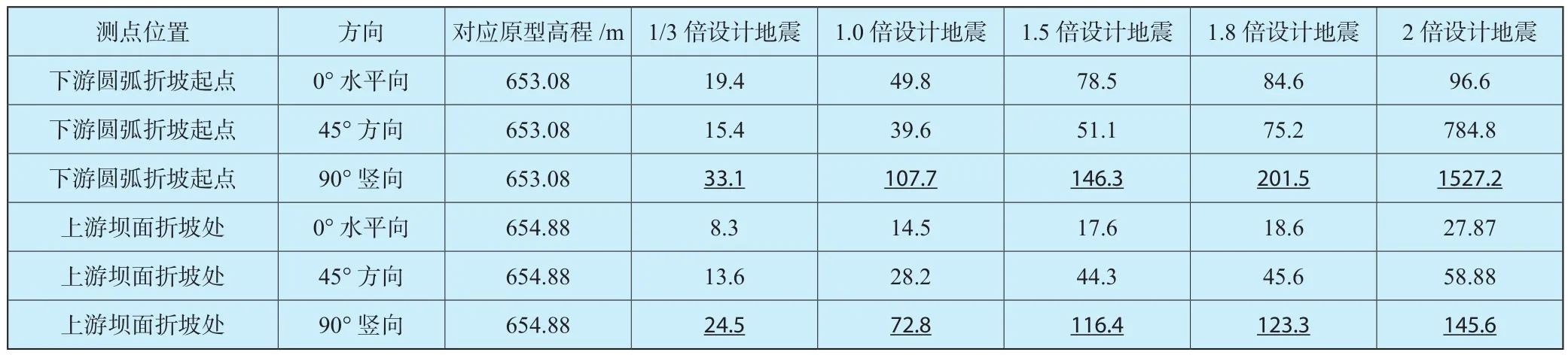
表2 地震波激振工况下的最大拉应变统计 单位 ：μεTable 2 Statistics of the maximum tensile strain under the condition of seismic wave excitation

从最大拉应变统计结果可以看出：

（1）在1/3倍设计地震阶段：在人工波顺河向激励下，坝体的最大拉应变为33με，发生在下游圆弧折坡起点处，上游坝面折坡处的最大拉应变为24.5με。结构沿纵向地震作用下不发生开裂，其响应处在线弹性范围内。

（2）1.0倍设计地震阶段：在人工波顺河向激励下，下游圆弧折坡起点处最大拉应变约为108με，超过峰值拉应变，表明下游圆弧折坡起点附近区域已产生细小裂隙，但肉眼无法看出。上游坝面折坡处的最大拉应变约为73με，与1/3倍设计地震工况的应变响应相比，坝体的最大拉应变响应是小震时的3倍，结构整体仍处于线弹性状态。

（3）1.5倍设计地震阶段：在人工波顺河向激励下，下游圆弧折坡起点处最大拉应变约为146με，上游坝面折坡处的最大拉应变约为116με，已超过混凝土的开裂应变，这两个部位裂隙在继续发展。

（4）1.8倍设计地震阶段：在人工波顺河向激励下，下游圆弧折坡起点处最大拉应变约为202με，上游坝面折坡处的最大拉应变约为123με，坝体局部裂隙进一步扩展，坝折坡点大部分区域进入弹塑性状态。

（5）2倍设计地震阶段：在人工波顺河向激励下，下游圆弧折坡起点处最大拉应变约为1527με，比设计小震（0.07g）最大拉应变增加了50倍左右，该部位塑性发展充分。

在该工况下，折坡点大部拉应变值达到开裂应变，出现肉眼可见的细小裂缝，从折坡点裂纹应变测点的应变曲线图（见图4）可以看出：试验过程中，在1.8倍设计地震下已经发生损伤的折坡点区域，裂纹明显扩展，应变曲线出现突变、拉压应力应变不再均衡。这是由于折坡点裂纹张开后，拉应变明显增大、压应变突降接近0。远离损伤区域的应变时程图拉压应变变幅差异不大，曲线图没有突变。折坡点裂纹张开过程，附近X4测点的加速度波形图（见图5）并不能看出有明显变化。

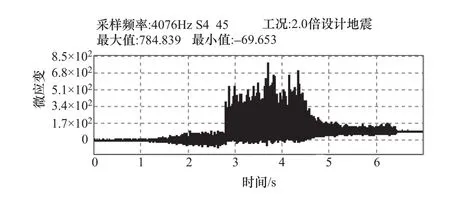
图4 2倍设计地震工况下应变测点时程图Figure 4 Strain time history of model under twice design earthquake

图5 2倍设计地震工况下加速度测点时程图Figure 5 Acceleration time history of model under twice design earthquake

（6）1.8倍设计地震场地波工况：在人工波顺河向激励下，坝段结构折坡点损伤破坏继续发生，并贯穿破坏。坝颈贯穿破坏后，坝颈裂缝从上游折坡下部向下游曲面连接段贯通发展，模型头部出现明显的破坏现象。

坝头部与坝体脱开后，原来完整的大坝相当于形成了两个质量体系，破坏后整个质量体系发生了质变，固有模态特性发生变异，体现在加速度、应变时程图上有明显的跳跃。

从1.8倍场地地震工况下典型部位的时程图（见图6和图7）可以看出：折坡点完全脱离的破坏时刻，加速度与应变在破坏前达到最大值，折坡点贯穿后该测点的加速度、应变发生突降。

而且，从破坏点处的应变曲线（见图6）可以看出，贯穿前，破坏点拉应变增大，在破坏瞬间拉应变下降后，随后压应变突然上升。之后拉应变基本消失，压应变得到释放，压应变也大幅减小。这表明在地震作用下，折坡点经受大幅振动后，拉应力超载，造成混凝土断裂，而断裂发生的瞬间，地震运动方向改变使得该处的裂隙上部质量对裂缝下部质量产生强大冲击，经过瞬间冲击，坝折坡处彻底贯穿，测点附近应变片断裂，应变曲线中断。在贯穿时刻，所有测点的响应，包括加速度（见图7）、压应变都有一个瞬间突变，特别是断裂区域附近测点响应，在突变时刻前后曲线有特别显著的差异。

图6 1.8倍场地地震工况下S4应变测点时程图Figure 6 Strain time history of measuring point S4 under 1.8 times field ground wave

3.3 频谱特性分析

在各个阶段试验完成前后，均用0.10～0.15g白噪声（120s）对模型进行频率探查，结构自振频率的变化在一定程度上也反映了模型结构经过不同工况激励后质量和刚度的变化。

从X8和X5测点的频谱图（见图8、图9）可以看出，频谱有两个峰值，体现了大坝模型前两阶固有模态频率。本文作者应用NeXT方法结合ITD法[12]求得W2白噪声工况下大坝模型沿着水平顺河向的前两阶模态，分别为91.6Hz和239.4Hz。第1阶模态振型表现为大坝整体沿顺河向晃动，第2阶模态则表现为坝顶的运动。

图8 X8测点1/3倍设计地震后白噪声探查频谱图Figure 8 Spectrum of measuring point X7 after 1/3 times design earthquake using white noise detection

图9 X5测点1/3倍设计地震后白噪声探查频谱图Figure 9 Spectrum of measuring point X5 after 1/3 times design earthquake using white noise detection

从频谱峰值频率统计表（见表3、表4）和曲线图（见图10）可以看出，大坝在遭遇不同幅值地震波激励后，随着大坝损伤逐渐加大，特别是折坡点损伤逐级加重的过程中，大坝白噪声频谱的峰值频率随之降低。

表3 不同阶段白噪声探查的频谱 第1阶峰值频率统计表Table 3 Statistical table of the first peak frequency of the spectrum in different stages of white noise detection

表4 不同阶段白噪声探查的频谱 第2阶峰值频率统计表Table 4 Statistical table of the second peak frequency of the spectrum in different stages of white noise detection

图10 频谱峰值频率变化曲线Figure 10 Variation curve of spectrum peak frequency

当大坝折坡点损伤完全贯通后，坝顶与坝顶以下部分形成了两个质量体系，各自频谱特征发生显著变化。裂缝下部的大坝整体部分的频谱（第1阶频谱峰值频率）有一定的升高，而坝顶质量运动产生频谱峰值（第2阶频谱峰值频率）随坝顶的脱离而消失（见图11）。而大坝顶部测点的频谱也因坝顶质量形成自由独立的质量块，峰值频率也急剧下降（见图12）。

图11 X8测点1.8倍场地地震后白噪声探查频谱图Figure 11 Spectrum of measuring point X7 after 1.8 times field ground wave using white noise detection

图12 X5测点1.8倍场地地震后白噪声探查频谱图Figure 12 Spectrum of measuring point X5 after 1.8 times field ground wave using white noise detection

可以看出，损伤发展会造成模型整体的模态特性发生变化，首先体现在结构固有频率发生下降。当发生断裂后，测点频率特性和时程曲线会发生显著突变。

3.4 动力放大系数变化规律分析

对不同阶段人工波激励下各点的加速度响应进行统计，得到不同测点的动力放大系数，如图13所示。由图可见，随着模型损伤发展，结构刚度下降，损伤区域的动力放大系数明显降低。本试验模型结构的破坏主要集中于重力坝应力集中的坝颈附近，损伤部位上部的动力放大系数与破坏前相比呈现明显下降，如坝顶测点的放大系数由4.3降低到2.5。

图13 不同阶段人工波激励下测点的动力放大系数Figure 13 Dynamic amplification coefficient of measuring point under artificial wave excitation in different stages

因此，大坝结构的动力放大系数变化也在一定程度上反映了大坝的损伤位置。

4 结束语

通过重力坝坝段振动台模型破坏试验，可以看出，结构在遭受地震破坏时，应变（或应力）时程、加速度时程、自振频率、频谱、动力放大系数等参数都发生显著变化。通过这些参数变化则可以进行损伤判别，为大坝健康诊断、大坝损伤快速识别、评估和定位提供依据。

通过本次试验，可以得到以下几点规律：

（1）大坝如果内部发生损伤，整体刚度会下降，大坝模态频率随之下降。

（2）大坝结构在地震中发生裂缝等损伤，地震响应和应变波形在破坏时刻有突变，破坏位置的动态应变波形会显现出单边特性、裂缝附近拉应力会急剧下降。

（3）大坝结构发生损伤后，损伤位置上部动力放大系数会明显下降。

本文仅对该问题作了探索性研究，尚有很多需要深入研究的地方。比如，深入分析不同参数对损伤状态判别的敏感度和可靠度，建立多参数联合损伤识别指标；建立完善的大坝强震监测系统，记录大坝正常状态下和强震前后大坝不同参数变化过程，根据参数变化曲线实时判断损伤发生时刻和损伤部位，为应急决策提供技术支持。