增压速率对多孔金属筛网泡破压力影响的实验研究

马原, 孙靖阳, 厉彦忠, 汪彬, 李杨

(1.西安交通大学制冷与低温工程系, 710049, 西安; 2.上海宇航系统工程研究所, 201109, 上海)

针对液体推进剂系统,航天器在轨点火、推进剂在轨传输等过程均需要单相液体的稳定供给。微重力条件下,气液相分布具有很大的随机性,必须采取推进剂管理技术对贮箱内的气液相进行控制与管理,才能保障单相液体的稳定获取[1-2]。筛网式液体获取装置(LAD)能够有效利用表面张力和毛细作用实现液相推进剂的持续获取,对于流体物性、轨道环境、流量需求等因素的敏感度较低,已经广泛应用于常温推进剂的在轨管理,并被认为是低温推进剂最理想的气液分离与全液获取方法[3-4]。

图1给出了一种四通道筛网式LAD的结构示意图[5]。贮箱内均匀布置4个液体获取通道,通道近壁侧安装有一层多孔金属筛网,其他面为金属固壁。由金属细丝编制而成的筛网具有大量微米级孔隙,能够依靠表面张力和毛细作用引流液体进入通道汇集于出液口,同时对气体发挥阻隔作用,从而实现气液分离与单相液体的获取。

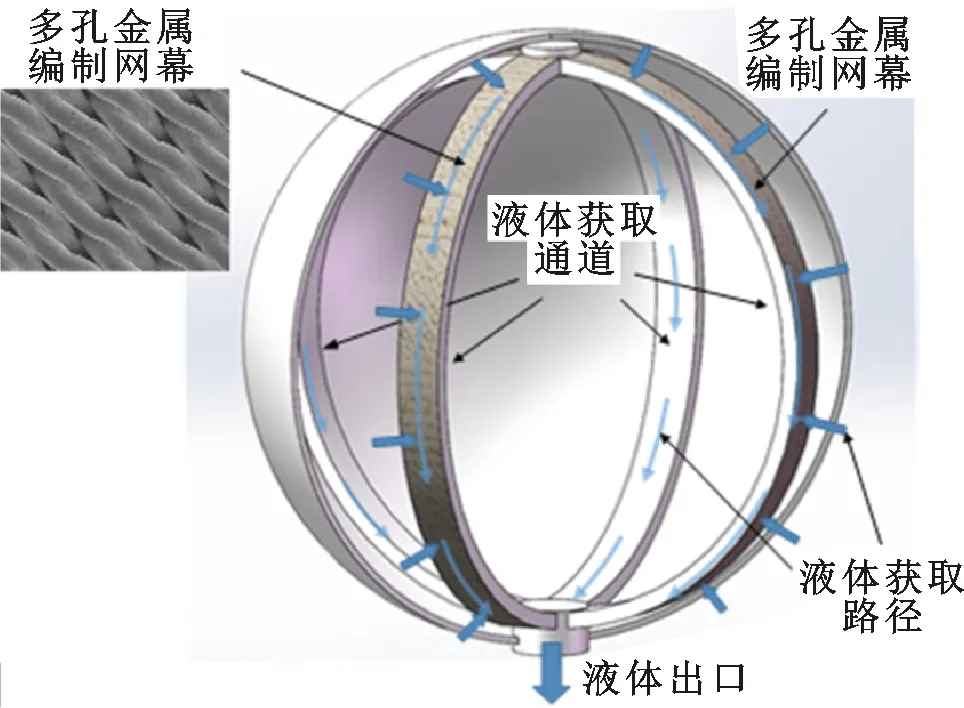
图1 筛网通道式LAD液体获取过程示意图[5]Fig.1 Schematic diagram of the liquid acquisition process of the screen channel LAD[5]

该装置的气体阻隔作用主要反映为金属筛网的泡破压力,泡破压力越大,气体阻隔能力越强[6]。早期,研究学者针对甲醇、水、硅油、氟利昂等多种常温流体开展了金属筛网泡破压力的实验研究[7-9]。随后,NASA研究人员先后对金属筛网在液氧、液态甲烷、液氮、液氢等低温流体内的泡破压力进行了实验研究,考察了筛网类型、流体温度、系统压力等因素对筛网泡破性能的影响规律[10-12]。然而,相关文献虽然提供了大量的泡破压力测量数据,但是并未针对泡破测量过程的特性规律以及实验数据处理方法给出详细介绍。

我国在低温推进剂气液管理方面的研究起步较晚,针对筛网式液体获取装置,Ma等对荷兰斜纹筛网(DTW)的液体芯吸特性开展了常温及低温实验测试,并构建了反映低温流体蒸发作用的芯吸计算模型[13-17]。针对筛网的泡破压力特性,国内尚未开展系统的深入研究。因此,本文针对3种编织密度的DTW筛网,采用异丙醇为实验工质,开展了不同增压速率下的泡破压力可视化测试,并基于静态泡破压力模型计算得到了3种筛网样本的有效微孔直径。相关工作可为LAD性能评估、设计优化以及空间低温系统方案设计提供理论依据和技术参考。

1 泡破压力预测模型

泡破压力ΔpBP是指第一个气泡穿透时筛网两侧的压差。图2给出了金属筛网内任一微孔的剖面示意。首先,液体(仅适用于与壁面接触角小于90°的润湿性液体)在毛细力驱动下能够完全填充孔隙并在孔隙中通流。在表面张力的作用下,气液界面两侧能够承受一定的压差,封阻气相的穿过。当气相侧压力不断升高使筛网两侧压差超过泡破压力时,孔隙内气液界面将无法继续阻止气体穿过,从而失去全液获取能力[9]。

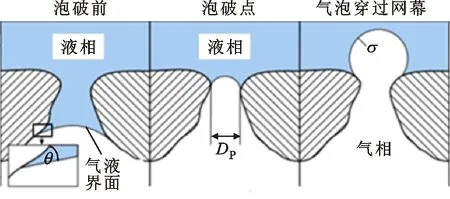
图2 气相穿透润湿筛网微尺度通道的过程示意图Fig.2 Schematic diagram of the bubble breakthrough across the micro-channel in the wet screen

基于毛细理论,两静态流体界面间因表面张力引起的压力差可以通过杨氏-拉普拉斯方程进行计算,合力方向指向界面凹面所指方向[18]。该压差与流体表面张力、界面曲率等因素有关,如下式所示

(1)

式中:p(+)、p(-)为界面凸侧、凹侧界面压力;σ为表面张力;Rmax、Rmin为界面最大、最小曲率半径。对于横截面为圆形的直毛细管(见图3),Rmax与Rmin相等,上式可以简化为[19]

(2)

式中:θ为接触角;dc为毛细管直径。

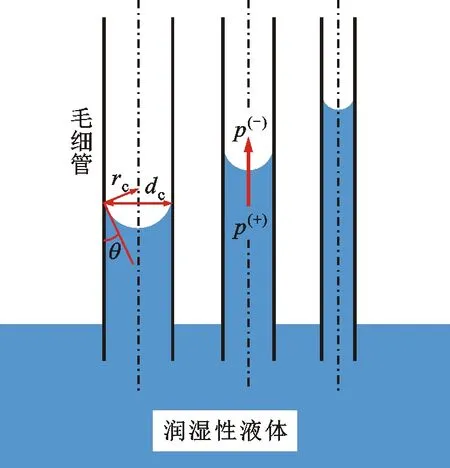
图3 润湿性液体毛细现象与界面特征Fig.3 Capillarity action and interface characteristics of wetting liquid

鉴于流体在筛网内的流动与毛细管流动的相似性,研究学者将筛网内部结构复杂的微尺度通道简化,假设为一组截面为圆形的直通道,且直径相同的毛细管束,基于式(2)提出了计算筛网静态泡破压力的简化模型[20]

(3)

式中DP为筛网有效微孔直径,即将筛网内复杂的三维通道结构等效简化为直通道的、横截面为圆形的毛细管对应的直径。DP由筛网编织结构决定,但并不是多孔筛网的客观结构参数,无法通过直接测量得到,通常采用测量泡破压力的方法由式(3)反算获得[21]。由于不锈钢材料热膨胀系数较小,应用于不同温区时不会产生明显的结构变化,即筛网DP基本不变[22]。经实验数据验证,式(3)能够广泛适用于多种常温与低温流体[7-12]。基于此,有研究学者首先采用常温标准溶液(如异丙醇)进行泡破压力测试,计算获得该筛网结构的DP后,替换低温流体物性对该筛网结构的低温泡破压力进行计算预测[23]。

2 泡破压力测试系统

实验系统如图4所示,主要包括液池、增压腔、压力调节系统和数据采集系统,增压腔通过支撑连杆固定于金属法兰下端。如图5所示,筛网样本通过可拆卸法兰配合铟丝密封安装于增压腔上端面,样本更换方便。筛网样本两侧布置有温度和压力测点。温度传感器采用Lakeshore铂电阻PT111,精度0.1 K。压差传感器采用EJA110E,精度0.055%。

图4 可视化泡破压力测试系统简图 Fig.4 Diagram of the visual testing system for bubble point pressure

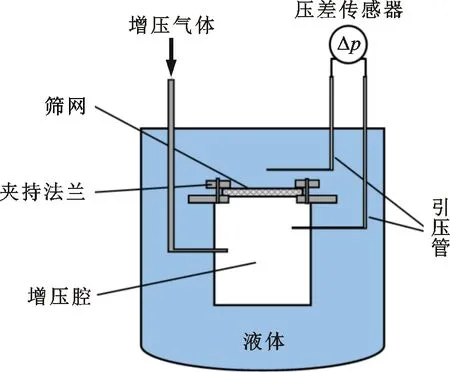
图5 筛网样本安装位置Fig.5 Installation site of the screen sample

开展实验时,首先加注液体至液位完全没过增压腔,待系统稳定后打开调节针阀向增压腔注入气体,建立增压腔内外压差,即筛网样本两侧压差。增压速率通过调节针阀开度进行控制。筛网样本上、下两侧压力分别由引压管引入压差传感器进行测量。增压过程中,当观测到有气泡冒出时表示筛网样本发生泡破,测量得到的筛网两侧压差数据即为泡破压力。

本次实验采用3种编织密度的DTW不锈钢筛网作为测试样本,具体参数列于表1。以DTW 200×600为例,表示一平方英寸(6.451 6 cm2)的筛网由200根经丝和600根纬丝编织而成。由于经纬丝直径和数量的差异,所形成的筛网有效微孔直径不同,导致不同筛网针对相同流体的泡破压力不同,如式(3)所示。实验工质采用异丙醇,相关物性参数列于表2。

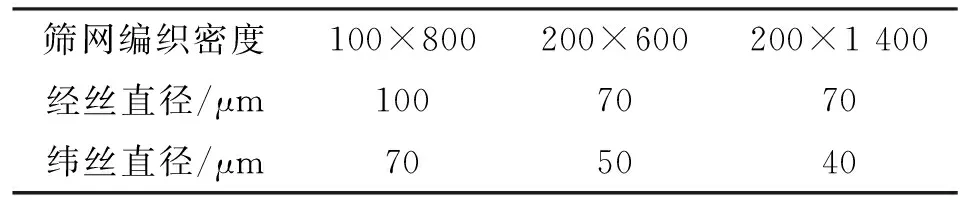
表1 DTW筛网样本结构参数

表2 异丙醇物性参数[23-24]

3 结果与讨论

本文针对3种筛网样本在异丙醇中的泡破特性开展了多组变工况测试。

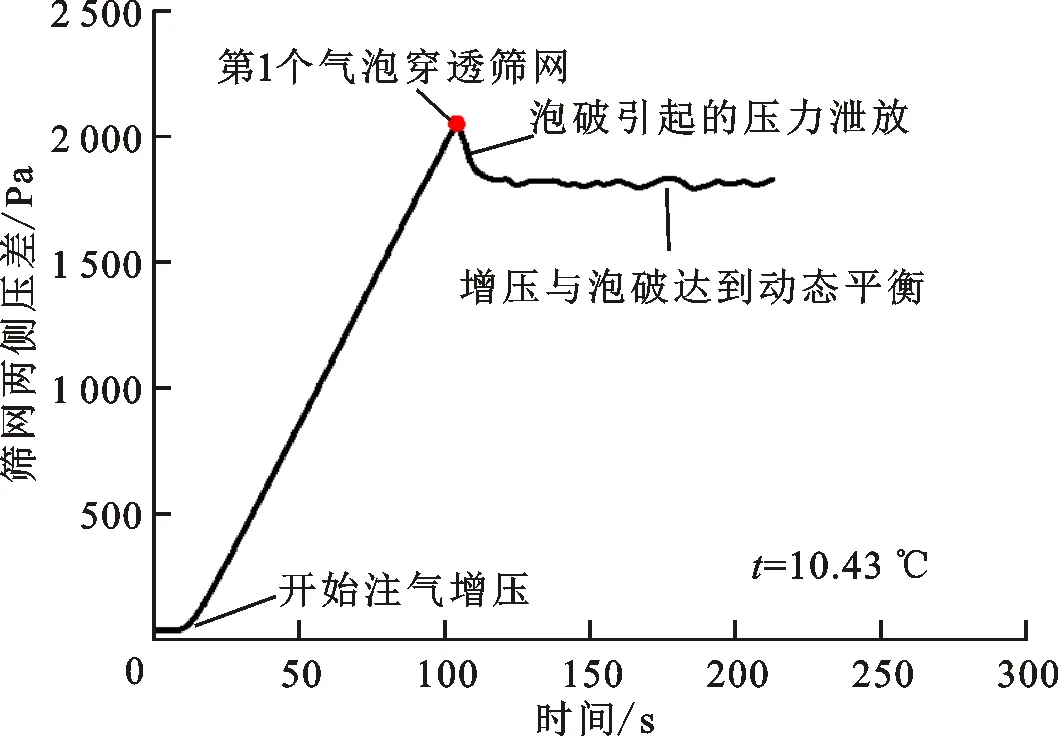
图6 泡破压力测试过程的典型数据曲线Fig.6 Typical data curve of the testing process of bubble point pressure

图6展示了一组DTW 200×600测量过程的压差数据。开始测试前,筛网两侧压差很小。在25 s左右打开进气阀,增压腔压力伴随气体注入不断上升,注气速率较为稳定,筛网两侧压差基本呈线性增长。图6所示工况的增压速率约为20 Pa·s-1,在100 s左右压差达到最大值,同时观察到筛网上有气泡溢出,这个压差峰值即为该工况下的泡破压力。伴随着泡破过程对增压腔的泄压作用,筛网两侧压差产生了一定程度的回落。随后,注气的增压作用与泡破的泄压作用逐渐达到动态平衡,筛网两侧压差在一定范围内稳定波动。

针对3种筛网样本,分别开展了多组不同增压速率下的泡破压力测试。以DTW 100×800筛网样本为例,取4组典型工况进行对比分析,结果如图7所示,可见增压速率较小的两组工况曲线呈现出与图6相似的变化规律。

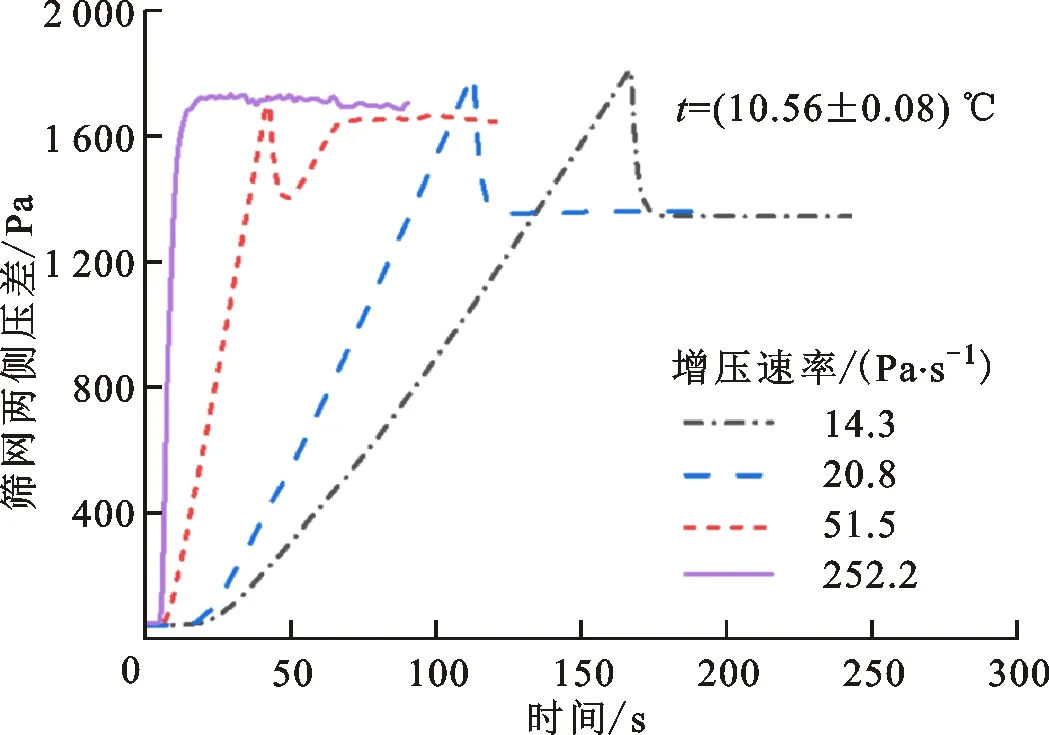
图7 不同增压速率下筛网压差数据曲线Fig.7 Curves of the pressure difference across screen at different pressurization rates

进一步提高增压速率,压差曲线虽然仍具有线性增压和达到峰值后回落的变化特点,但最终达到动态稳定的压差明显高于低增压速率工况的稳定值(51.5 Pa·s-1工况曲线)。这主要是由于流量越大,筛网流动阻力越大引起的。当增压速率继续增大至一定值后,筛网压差转变为迅速升高后逐渐趋于稳定波动的变化规律,不再具有明显的峰值特点(252.2 Pa·s-1工况曲线),最终达到的动态稳定值也更高。

图8展示了不同增压速率下DTW 100×800筛网泡破过程的气泡状态。当增压速率较小时,个别位置轻度泡破的泄压能力即可平衡注气增压的作用,动态稳定过程的压力波动幅度很小。随着增压速率的增大,筛网泡破的范围和强度均随之增大,从而以更强的泄压能力抵消不断提高的增压作用,其动态平衡过程的不稳定性也就越大。

进一步分析各组数据发现,3种筛网样本在不同增压速率下测量得到的泡破压力呈现出了相似的变化规律,均为先线性降低后趋于稳定,如图9所示。由图可知,在增压速率较小的一定范围内,提高增压速率,将导致筛网在更低的压差下发生泡破,即筛网气泡阻隔能力下降,当增压速率增大到一定程度后,将不再对泡破压力产生明显的影响。

(a)1.26 Pa·s-1 (b)14.3 Pa·s-1

(c)51.5 Pa·s-1 (d)252.2 Pa·s-1图8 不同增压速率下筛网泡破现象Fig.8 Bubble breakthrough across screen at different pressurization rates

由于式(3)为静态泡破压力的计算模型,当利用该式求解筛网的有效微孔直径时,理论上应代入增压速率为零时测得的泡破压力。也就是说,理论上,静态泡破压力是无法通过实验测量准确获得的。因此,本文采用线性拟合方法对不同筛网的静态泡破压力进行计算预测。由于泡破压力随增压速率的线性变化关系仅在较低增压速率范围内较为明显,结合不同增压速率下压差数据的变化特征(见图7),仅取具有图6典型曲线特征的测量数据进行拟合。线性拟合结果已在图9中注明,线性相关系数R2均大于0.95,反映了良好的线性度关系。

表3列出了3种筛网在异丙醇工质内的静态泡破压力,即图9中线性拟合式的截距。同时,表3还列出了将静态泡破压力和流体物性参数代入式(3)计算得到的有效微孔直径。可以看出,随着筛网编织密度的增加,筛网有效微孔直径减小,泡破压力增大。也就是说,编织越密的筛网具有更强的气体阻隔能力。

表3 3种筛网样本的静态泡破压力和有效微孔直径

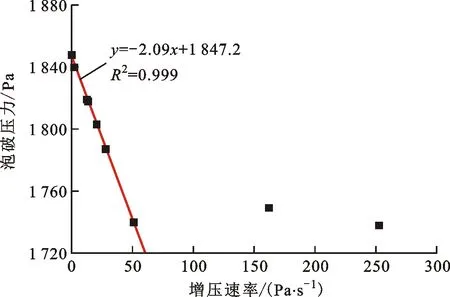
(a)DTW 100×800,t=(10.56±0.08) ℃

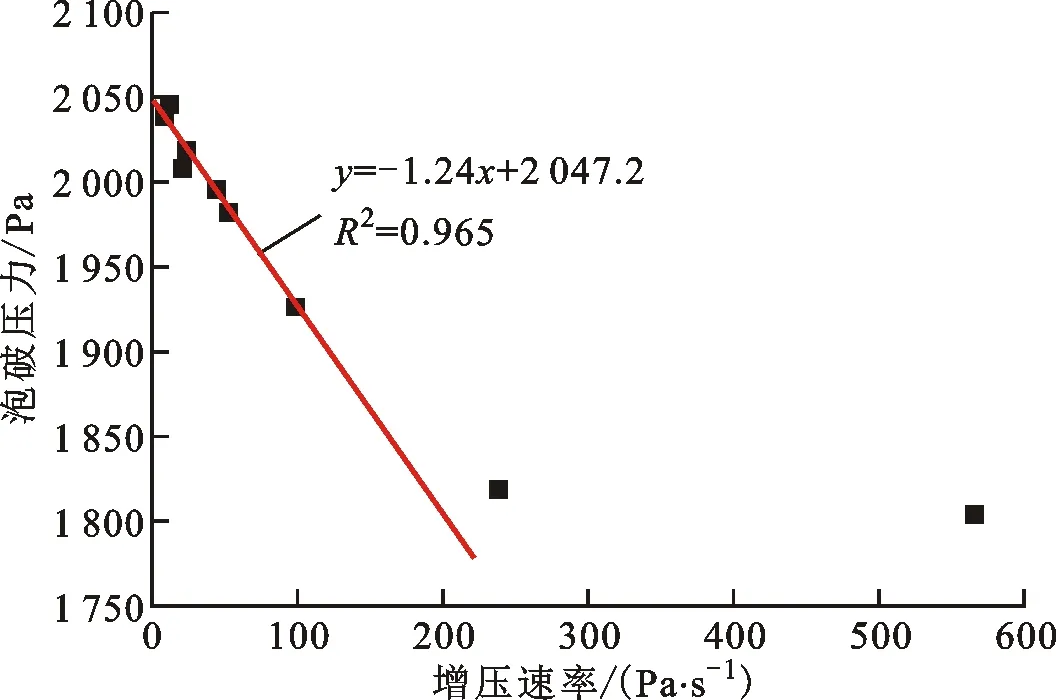
(b)DTW 200×600,t=(10.38±0.15) ℃

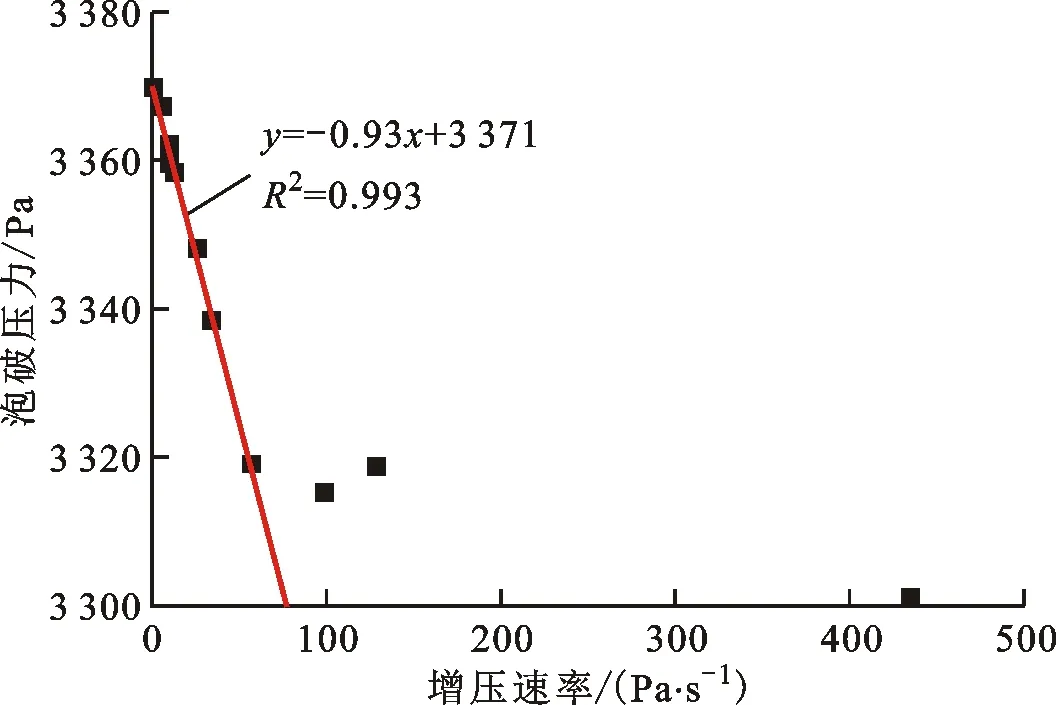
(c)DTW 200×1 400,t=(10.64±0.33) ℃图9 泡破压力与增压速率的关系 Fig.9 Relationship between bubble point pressure and pressurization rate

4 结束语

本文针对DTW 100×800、200×600和200×1 400共3种编织密度的不锈钢筛网,以异丙醇为工质,进行了不同增压速率下的泡破压力测试,主要结论如下。

(1)随着增压速率的升高,筛网样本在异丙醇液体中的泡破压力呈现出先降低后趋于稳定的变化规律,筛网泡破强度不断增大,从局部小气泡溢出逐渐转变为大面积剧烈泡破。

(2)在增压速率较低时,泡破压力随增压速率呈现出良好的线性递减趋势,通过数据线性拟合,得到了3种筛网样本在异丙醇液体中的静态泡破压力,静态泡破压力高于动态泡破压力。

(3)随着筛网编织密度的增加,筛网有效微孔直径逐渐降低,泡破压力逐渐增大,体现出更强的气体阻隔能力。基于本文获得的有效微孔直径,可以通过式(3)对3种筛网在不同流体内的泡破特性进行初步预测。